Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.


20 21
10.4.ВОЗМОЖНЫЕ СОСТОЯНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
ВНЕШНЕЕ ВОЗДЕЙСТВИЕ ОТСУТСТВУЕТ
Если внешнее воздействие отсутствует
,0)(
~
tg (10.34)
то имеем автономную нелинейную систему, которая в соответствии
с формулами (10.32),(10.34) описывается уравнением
. )( Ф )(
0
dtxktx
aa
(10.35)
Оно может иметь решения
1
:
1 – Стационарное (одно или несколько),
2 – Периодическое (нестационарные), которое называют ав-
токолебательным.
Стационарное решение
const)(
aa
xtx
(10.38)
найдём из уравнения (10.35)
. Ф)(
0
dkxtx
aa
(10.39)
Так как передаточная функция линейной части системы равна
,
0
τ
dekpW
p
(10.40)
то для 0
p имеем
0
. dkpW
(10.41)
Поэтому из уравнения (10.40) следует
.
)0(
1
Ф
aa
x
W
x
(10.42)
1
Отметим, что для линейной системы уравнение (10.35) принимает вид
. )(
0
dtxktx
aa
(10.36)
и имеет только одно единственное решение
.0
a
x
(10.37)
,1
4
,2sin
2
1
2
Г
Г
A
b
A
kb
K
k
К
C
S
(10.30)
где
tgk ,
A
b2
1arcsin
.
10.3 УРАВНЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
В предыдущей главе уравнение ошибки (9.5) замкнутой сис-
темы с одной нелинейностью (рис.9.1) было записано во времен-
ной области в таком виде
dxtktgtx
t
)(Ф )()(
0
, (10.31)
где
)()(
1
sWLtk
- импульсная (весовая) функция линейной час-
ти системы, )(tg - внешнее воздействие.
Здесь предполагается, что внешнее воздействие, приложено
ко входу нелинейной автоматической системы в момент 0
t , а до
этого момента система находилась в покое.
При обозначении через )(
~
)( tgtg
неисчезающее внешнее
воздействие, приложенное к системе в момент
t
, и замене
переменных (
t
на
и
на
t
) уравнение вынужденногоо
процесса примет вид
dxtktgtx )(Ф )(
~
)(
0
в
(10.32)
Момент наблюдения в этом уравнении отстоит от момента
приложения воздействия на бесконечно большой промежуток вре-
мени.
Под свободным процессом в системе будет пониматься раз-
ность между общим )(tx и вынужденным данным
)(
в
tx
процес-с-
сами
).()()(
в
txtxtx
с
(10.33)

22 23
ВНЕШНЕЕ ВОЗДЕЙСТВИЕ ОТЛИЧНО ОТ НУЛЯ
1.Внешнее воздействие стационарно
В исходном уравнении (10.32) положим
const.)(
~
ctg (10.45)
Стационарное решение
Решение уравнения (10.32) может быть стационарным
const.)(
вв
xtx
(10.46)
С учётом (10.41) получим
)0()(Ф
вв
Wxcx
или
.
)0(
Ф
в
в
W
xc
x
(10.47)
Графическое решение уравнения (10.47) приведено на
рис.10.24.
Если линейная система астатическая, т.е.
,)0(
W
то из
уравнения (10.47) имеем
.0Ф
в
x
(10.48)
в
Ф xy
в
1
x
в
2
x
в
3
x
в
4
x
0
)0(
в
W
xc
0)0(
W
0)0(
W
в
x
в
Ф x
с
Рис.10.24.Графическое решение уравнения (10.47)
Множитель в правой части этого уравнения
)0(
1
W
k
c
мож-
но рассматривать как коэффициент статической линеаризации не-
линейности
.Ф
aca
xkx
(10.43)
На рис.10.23 даётся графическое решение уравнения (10.43).
При
0
c
k
(
0)0(
W
- имеем положительную обратную связь)
абциссы точек пересечения нелинейной зависимости
a
xФ
и пря-
мой
ac
xky
соответствуют четырём возможным стандартным
решениям
.4,3,2,1,const ix
a
i
При
0
c
k
(
0)0(
W
) имеем единственное состояние равно-
весия .0
a
x
Уравнение (10.35) может иметь, как будет показано ниже, и
периодическое (в общем случае несинусоидальное) решение, пер-
вая гармоника которого имеет вид
.sin)(
~
tAtx
a
(10.44)
Амплитуда и частота этого решения определяются внутрен-
ними свойствами системы (как линейной так и нелинейной её ча-
стей).
a
xy Ф
0
c
k
a
x
1
a
x
2
a
x
3
a
x
4
ac
xky
0
c
k
a
x
0
Рис.10.23.Графическое решение уравнения (10.43)

24 25
ГЛАВА ОДИНАДЦАТАЯ
АВТОНОМНЫЕ ПЕРИОДИЧЕСКИЕ
ПРОЦЕССЫ-АВТОКОЛЕБАНИЯ
11.1. УСЛОВИЯ СУЩЕСТВОВАНИЯ АВТОКОЛЕБАНИЙ
(ГАРМОНИЧЕСКИЙ БАЛАНС ДЛЯ АВТОКОЛЕБАНИЙ)
В предыдущей главе было показано, что установившиеся про-
цессы в автономной нелинейной системе вида рис.10.1 описыва-
ются нелинейным уравнением
. Ф
0
dtxktx
aa
(11.1)
Точное его решение для произвольной характеристики нели-
нейного звена
)(xy Ф
(11.2)
возможно только численными методами. Приближённое решение
может быть найдено с помощью метода гармонической линеариза-
ции нелинейности. Чем ближе автономный периодический процесс
к гармоническому (чем слабее в нём представлены высшие гармо-
нические), тем точнее будет приближённое решение. Метод гармо-
нической линеаризации даёт наиболее адекватную аппроксимацию
нелинейности при периодических процессах, поэтому он наилуч-
шим образом приспособлен для исследования этих процессов.
Будем искать периодическое установившееся решение урав-
нения (11.1) в виде первой гармоники (пренебрегая высшими гар-
моническими)
,sin)(
~
tAtx
a
(11.3)
которую в комплексной (символической) форме представим так
.)(
~
tja
Aetx
(11.4)
Нелинейная функция (10.2) в соответствии с методом гармо-
нической линеаризации аппроксимируется зависимостью
.
~
~
Г
txAkty
a
(11.5)
Для однозначных нелинейностей с характеристиками, прохо-
дящими через начало координат, решение уравнения (10.48) толь-
ко одно
.0
в
x
(10.49)
Следовательно, в нелинейной астатической системе ошибка
остаётся равной нулю (как и в линейной системе) при изменении
внешнего воздействия
.)(
~
ctg
При конечном значении
)0(W
изменение постоянного внеш-
него воздействия будет приводить, как видно из рис.10.24, к вари-
ации решений
0
в
i
x
в том числе и в случае, если
0)0(
W
.
Периодическое решение (автоколебания)
При изменении постоянного (стационарного) внешнего воздей-
ствия возможно изменение амплитуды и частоты автоколебаний
.sin)(
~
tAtx
2.Внешнее воздействие периодическое
При переодическом внешнем воздействии
tAtg
ПП
sin)(
~
уравнение (10.32) имеет решение:
а) Принуждённое периодическое с частотой
П
или мень-
шей её в целое число раз(с частотой субгармоник). Периодическое
воздействие может подавить автоколебания, которые были в
системе при .0)(
~
tg Режим подавления автоколебаний называ-
ется режимом принудительной синхронизации на основной час-
тоте
П
или на частоте субгармоник (
к
п
сг
, 1
k ).
б) Принуждённое периодическое и автоколебательное. Режим
совместного существования этих двух периодических решений на
разных частотах (
п
(
сг
),
) называют режимом биений.

26 27
.
,
Г
A
AWAkA
(11.8)
Первое из них выражает баланс амплитуд, второе - баланс
фаз. Соотношения (11.6) и (11.8) называются соотношениями гар-
монического баланса при автоколебаниях. Они позволяют оп-
ределить амплитуду
a
A
и частоту
a
возможных автоколебаний.
Согласно критерию Найквиста уравнение (11.6) указывает, что гар-
монически линеаризованная замкнутая система рис.10.1 находит-
ся на границе устойчивости. Отсюда следует, что условие суще-
ствования автоколебаний (11.6) требует таких изменений
частоты
и коэффициента гармонической линеаризации (за
счёт изменения амплитуды
A
), при которых гармонически ли-
неаризованная нелинейная система выводится на границу ус-
тойчивости.
11.2. ОПРЕДЕЛЕНИЕ АМПЛИТУДЫ, ЧАСТОТЫ И
УСТОЙЧИВОСТИ АВТОКОЛЕБАНИЙ
ЧАСТОТНЫЙ СПОСОБ
(МЕТОД Л.С.ГОЛЬДФАРБА)
Запишем условие суще-
ствования гармонического ре-
жима (11.6) в следующей фор-
ме
).(
)(
1
Г
jW
AK
(11.9)
Изобразим на комплекс-
ной плоскости левую и правую
части этого уравнения, фиксируя первую для различных значений
амплитуд
A
, вторую - для различных частот
(рис. 11.1).
Точка пересечения этих двух кривых определит частоту wа
(по оцифровке кривой
jW
) и амплитуду
a
A
(по оцифровке кри-
вой
)(
1
Г
AK
) возможных автоколебаний.
Рис.11.1.К определению частоты
амплитуды автоколебаний
jW
+j
A
+1
A
)(
1
Г
AK
0
),(
aa
A
Подставляя формулы (11.4),(11.5) в уравнение (11.1)получим
0
τГ
dAeAkkAe
tjtj
или
.
0
τГ
dekAeAkAe
jtjtj
Принимая во внимание выражение для частотной характери-
стики линейной части системы
,
0
τ
dekjW
j
находим условие существования гармонического режима в авто-
номной нелинейной системе
jWAk 1
Г
(11.6)
Это условие имеет ясный физический смысл. Правая часть
выражения (11.6) представляет собой частотную характеристику
разомкнутой гармонически линеаризованной системы, на вход ко-
торой воздействует гармоническое колебание (11.4) (рис.11.1).
Выходная величина
tz
~
будет иметь, согласно (11.6), ту жее
амплитуду, но сдвинута по фазе на угол
.
tAtz sin
~
(11.7)
Имея в виду, что
θj
eWjW
,
комплексному условию (11.6) будут соответствовать два веществен-
ных
Ak
Г
jW
)(
~
tx
a
)(
~
ty
)(
~
tz
Рис.11.1. Частотная характеристика разомкнутой гармонически
линеаризованной нелинейной системы
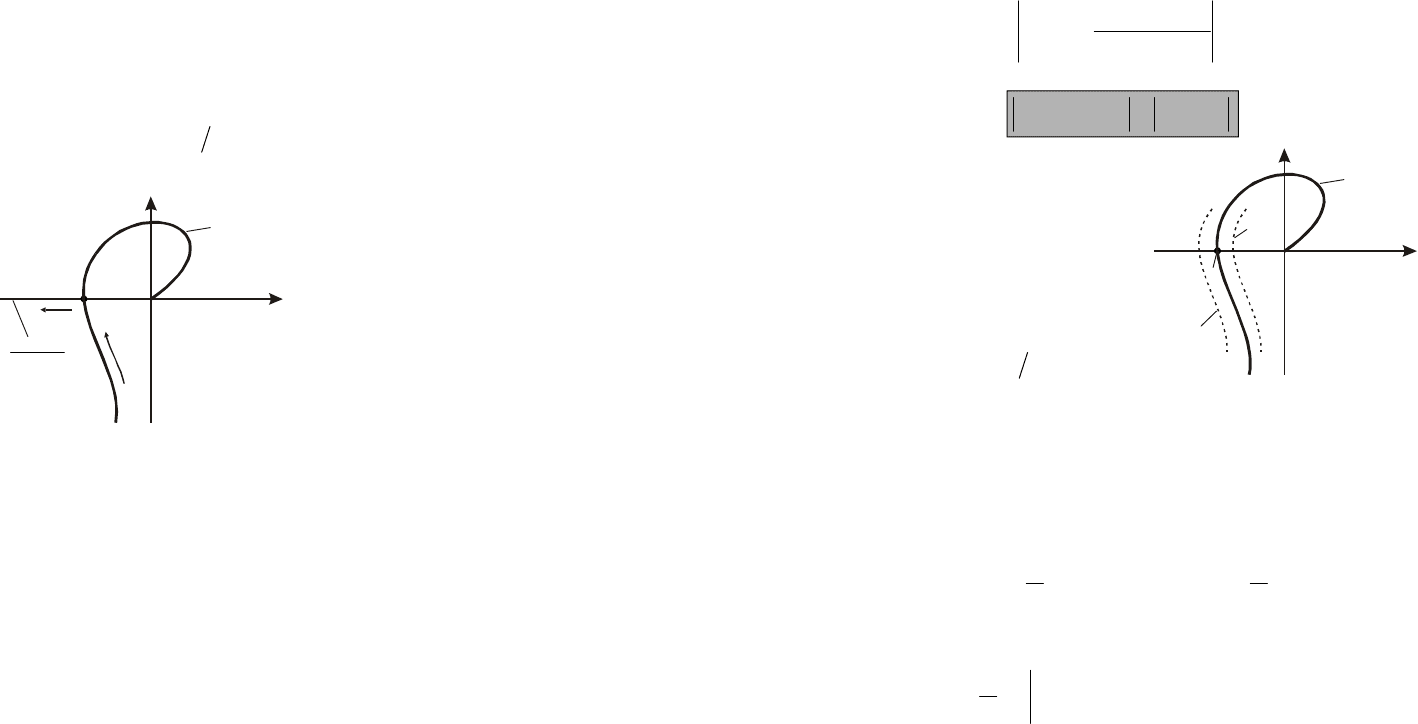
28 29
будет выполняться. Очевидно при 0
A частотная характеристи-
ка деформируется так, что критерий Найквиста будет нарушен
(рис.11.3).
Следовательно, автоколебания будут устойчивы, если при
0
A
1
)(
1
)(
Г
AAK
jW
a
a
или
.)()(
Г aa
jWAAK
(11.11)
Неравенство(11.11) можно
рассматривать как амплитудно-
частотный критерий устойчиво-
сти автоколебаний.
В соответствии с ним на
рис. 11.1 точка
a
A
,
a
соответ-
ствует устойчивому автоколеба-
нию, если увеличение амплиту-
ды вдоль кривой
Г
1 K
соот-
ветствует направлению во вне-
шность кривой.
АЛГЕБРАИЧЕСКИЙ СПОСОБ
Введем понятие передаточной функции гармонически линеа-
ризованного нелинейного звена
.)()(),(
ГГГ
p
AKAKA
p
K
CS
(11.12)
При
j
p
эта передаточная функция совпадает с коэффи-
циентом гармонической линеаризации
).()()(),(
ГГГГ
AKAjKAKA
p
K
CS
jp
(11.13)
В отличие от коэффициента гармонической линеаризации
)(
Г
AK
, передаточная функция гармонически линеаризованногоо
нелинейного звена зависит не только от амплитуды, но и от часто-
ты автоколебаний.
Рис.11.3.Оценка устойчивости
автоколебаний
+j
+1
jW
0
0
A
0
A
–1
Этот метод особенно удобен для оценки влияния параметров
нелинейности и линейной части на частоту и амплитуду автоколе-
баний. Отсутствие пересечения двух указанных кривых свидетель-
ствует об отсутствии автоколебаний.
Особенно просто определение амплитуд и частот возможных
автоколебаний в нелинейных системах с однозначной характерис-
тикой нелинейного звена. В этом случае
),()()( ;0)(
ГГГГ
AKAKAKAK
SC
т.е. коэффициент гармонической линеаризации вещественен.
Следовательно
)(1
Г
AK
совпадает с вещественной осью
комплексной плоскости (рис. 11.2).
Параметры автоколебаний
a
,
a
A
(если автоколебания воз-
можны) определяются свой-
ствами только линейной части
системы и не зависят от одно-
значной характеристики нели-
нейного звена.
После определения пара-
метров периодического реше-
ния нужно исследовать его ус-
тойчивость.
Как отмечалось выше, ам-
плитудно-фазовая характерис-
тика гармонически линеаризо-
ванной нелинейной системы с разомкнутой обратной связью
)()(),(
Г
jWAKAjW
(11.10)
проходит через точку (-1) при наличии автоколебаний.
Замкнутая нелинейная система в этом случае находится на
границе устойчивости. Дадим некоторое приращение амплитуде
автоколебаний
A
. Если 0
A и автоколебания устойчивы, то воз-
росшая скачком амплитуда должна уменьшиться до нижнего не-
возмущенного значения. В этом случае частотная характеристи-
ка
),( AAjW
пройдет мимо точки -1 и займет положение
правее точки -1, при котором критерий устойчивости Найквиста
Рис.11.2.Определение параметров
автоколебаний в системе с
однозначной характеристикой
нелинейного звена
jW
+1
A
)(
1
Г
AK
),(
aa
A
0
+j

30 31
В уравнения (11.20) можно ввести какие-либо параметры си-
стемы, например, коэффициент усиления
,0),,(
kAX .0),,(
kAY (11.21)
В результате представляется возможным найти зависимости
),(kAA
)(k
и построить соответствующие графики (рис.11.4).
На основании этих графиков можно выбрать параметр k та-
ким, чтобы:
1 – амплитуда автоколебаний была достаточно малой,
2 – частота их не была опасной для данной системы,
3 – автоколебаний не было вовсе (
гр
kk
).
Можно решить уравнения (11.20) с учетом двух каких-либо
параметров ( k и
T
)
,0),,,(
TkAx .0),,,(
TkAy (11.22)
Уравнения (11.22) позволяют строить линии равных значений
A
и
на плоскости этих параметров k и
T
(рис.11.5).
Семейство кривых на рис.11.5 дает информацию для выбора
значений указанных параметров k и
T
.
Для исследования устойчивости периодического решения
(11.17) дадим малые начальные отклонения
A
и
частоты. Бу-у-
дем иметь
.)sin()(
~
ξ
teAAx
ta
(11.23)
Рис.11.4.Зависимость параметров автоколебаний
((а)-амплитуды; (б)-частоты) от коэффициента усиления
0
k
гр
k
б)
A
0
k
гр
k
а)
Передаточная функция разомкнутой нелинейной системы равна
),(),()(
Г
pWA
p
KPW
(11.14)
где
)(
)(
)(
pQ
pR
pW - передаточная функция линейной части.
Передаточная функция замкнутой системы определяется из
выражения
,
)(),()(
)(),(
)(
)(
),(1
)(
)(
),(
)(1
)(
Г
Г
Г
Г
pRA
p
KpQ
pRA
p
K
pQ
pR
A
p
K
pQ
pR
A
p
K
pW
pW
(11.15)
из которого получаем характеристическое уравнение замкнутой
системы
.0)(),()()(
Г
pRA
p
KpQpD
(11.16)
Периодическому решению
tAtx
a
sin)(
~
(11.17)
соответствует пара чисто мнимых корней
jp
2,1
характе-
ристического уравнения (11.16).
Для отыскания показателей периодического решения ),(
A
примем в характеристическом уравнении
j
p
.
Получим
.0)()()()(
ГГ
jRAjKAKjQ
CS
(11.18)
Выделим в этом выражении вещественную ),(
AX и мни-
мую ),(
AY части
.0),(),(
AjYAX (11.19)
Уравнение (11.19) эквивалентно двум
;0),(
AX ,0),(
AY (11.20)
решение которых позволит определить параметры автоколебания
A
и
.
Если уравнения (11.20) не имеют положительных веществен-
ных решений для
A
и
, то автоколебания в данной системе не-
возможны.

32 33
Из этого выражения следует, что одинаковость знаков
и
A
обеспечивается при выполнении неравенства
.0
**
x
A
yy
A
x
(11.27)
В дополнению к этому условию нужно также потребовать,
чтобы все остальные корни характеристического уравнения (11.16)
были левыми, т.е. чтобы многочлен
22
1
)(
)(
p
pD
pD
(11.28)
удовлетворял критерию Гурвица (или Михайлова).
Таким образом, критерием устойчивости автоколебания бу-
дет неравенство (11.27) и нахождение корней полинома (11.28) в
левой полуплоскости.
ГРАФИЧЕСКИЙ СПОСОБ
(ИСПОЛЬЗОВАНИЕ КРИВОЙ МИХАЙЛОВА)
Характеристический полином замкнутой нелинейной систе-
мы, как следует из выражения (11.15), имеет вид
).(),()()(
Г
pRA
p
KpQpD
(11.29)
Произведя в (11.29) подстановку
~
jp
(
~
- текущее значе-
ние частоты), получим формулу для кривой Михайлова
)
~
(),
~
()
~
()
~
(
Г
jRA
j
KjQjD
(11.30)
Если мы найдем такие значения
a
~
и
a
A
A
, при ко-о-
торых кривая Михайлова проходит через начало координат (рис. 11.6),
то
a
и
a
A
являются параметрами автоколебательного режимаа
.sin
~
tAx
aaa
(11.31)
Действительно, во-первых, прохождение кривой Михайлова
через начало координат свидетельствует о нахождении системы на
границе устойчивости, т.е. в автоколебательном режиме; во-вто-
рых, поскольку в начале координат имеем у кривой
,
~
(11.32)
то именно на этой частоте возникает автоколебательный процесс
(11.31).
Полученное выражение
описывает колебательный пере-
ходный процесс при малом от-
клонении от периодического ре-
жима (11.17). Этот режим будет
устойчивым, если знаки вели-
чин
,
,
A
одинаковы. Дей-ей-
ствительно, при скачкообразном
начальном (в момент 0
t ) воз-
растании амплитуды на величи-
ну 0
A будем иметь в пере-
ходном процессе уменьшение
амплитуды
t
eAA
ξ
)(
, если коэффициент затухания
будет по-
ложительным. Аналогичная ситуация возникает, если отрицатель-
ному
A
будет соответствовать отрицательное же значение
.
В символической записи уравнение (11.23) будет иметь вид
,)(
~
)ξωω( tjja
eAAx
(11.24)
в котором
ξω j
можно рассматривать как комплексное прира-
щение частоты.
Уравнение (11.19) при приращениях амплитуды и частоты за-
пишется
.0),(),(
jAAjyjAAx (11.25)
При разложении (11.25) в ряд Тейлора получим с учетом (11.19)
,0)()(
****
j
y
jA
A
y
jj
x
A
A
x
(11.26)
где знак * означает, что частные производные берутся при значе-
ниях
A
и
периодического режима.а.
Выделяя в (11.26) вещественную и мнимую части и исключая
из полученных двух уравнений величину
ω
, найдем
.
2*2*
**
A
yx
x
A
yy
A
x
k
0
4
A
1
ω
T
2
3
4
3
A
2
A
1
A
Рис.11.5.Линии равных значений
амплитуды и частоты
автоколебаний на плоскости двух
параметров T и k.

34 35
начало координат, то система
будет устойчивой - приращение
A
будет в переходном процес-
се уменьшаться до нуля. Если
же при
0
A
кривая займет
положение 2 (проходя мимо на-
чала координат), то система не-
устойчива - скачком возникшее
приращение
A
будет продол-
жать увеличиваться.
При
0
A
в устойчивой
системе кривая займет положе-
ние 2, - в неустойчивой систе-
ме - положение 1.
1
2
+j
+1
0
a
A
A
0
A
A
A
a
A
A
A
a
Рис.11.7.Определение
устойчивости
автоколебательного процесса
с помощью кривой Михайлова
+j +j
+1
+1
a
A
A
a
~
1
A
a
A
a
0
0
~
2
A
3
A
1
2
A
B
D
0
а) б)
Рис11.6.Определение параметров автоколебания
с помощью кривой Михайлова
Безусловное выполнение равенства (11.32) в начале коорди-
нат дает основание ввести в рассмотрение вместо кривой Михай-
лова другую кривую, у которой всегда имеем
~
:
).()()()(
Г
jRAKjQjf
(11.33)
Использование этой кривой упрощает нахождение парамет-
ров автоколебательного режима. Теперь нужно только подобрать
такое значение
a
A
A
, при котором кривая (11.33) пройдет черезз
начало координат (рис. 11.6,б). Ориентировочно имеем
),(
232
AA
AB
AO
AA
a
),(
121
CD
CO
a
где
321
AAA
- амплитуды трех кривых )(
jf . За
a
при-
мем значение
, при котором )(
jf =0.
Кривая (11.33) позволяет исследовать и устойчивость автоко-
лебательного процесса (11.31).
При
a
A
A
эта кривая проходит через начало координатт
(рис.11.7). Дадим приращение
A
амплитуде
a
A
:
.AAA
a
В зависимости от знака
A
кривая (11.33) займет положение
1 или 2. Если при
0
A
кривая занимает положение 1, обходя

36 37
где
0
)()( dekjW
в
j
в
τω
- частотная характеристика линейной
части системы.
Уравнение (12.5) может быть записано также в форме
).(
)()(1
1
)(
~
tg
AKjW
tx
в
в
Г
(12.6)
Это уравение для ошибки нелинейной замкнутой системы
можно непосредственно получить из блок - схемы рис.10.1, если
нелинейное звено заменить гармоническим коэффициентом пере-
дачи. Из уравнения (12.5) после подстановок (12.3) и сокращения
на
tj
b
e
получим соотношение гармонического баланса при вы-
нужденных гармонических колебаниях:
j
b
e
A
B
AKjW )()(1
Г
(12.7)
При отсутствии внешнего воздействия ( 0
B ) это соотноше-
ние будет совпадать с аналогичным (11.6) для автоколебаний.
Соотношение гармонического баланса для вынужденных ко-
лебаний (12.7) позволяет определить амплитуду
A
и фазу
вы-
нужденных колебаний при заданной амплитуде
B
и частоте
в
,
внешнего гармонического воздействия.
12.2.МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЯ
ГАРМОНИЧЕСКОГО БАЛАНСА
ГРАФИЧЕСКИЙ МЕТОД
Запишем соотношение гармонического баланса при вынуж-
денных колебаниях (12.7) в таком виде:
.)]()(1[
jГ
в
BeAAKjW
(12.8)
Левая часть этого уравнения
AAKjWAZ
Г
вв
)]()(1[),(
(12.9)
является функцией амплитуды и частотой вынужденных колеба-
ний ошибки
в
x .
ГЛАВА ДВЕНАДЦАТАЯ
ВЫНУЖДЕННЫЕ ПЕРИОДИЧЕСКИЕ ПРОЦЕССЫ
Обратим внимание, что в нелинейных системах принцип сло-
жения (суперпозиции) решений несправедлив, поэтому нельзя скла-
дывать свободные и принужденные (вынужденные) колебания.
Будем рассматривать одночастотные принужденные колеба-
ния, полагая, что их форма близка к синусоидальной из-за фильт-
рующих свойств линейной части системы.
12.1.ГАРМОНИЧЕСКИЙ БАЛАНС ДЛЯ
ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
Пусть на входе нелинейной автоматической системы (рис. 10.1)
имеем внешнее гармоническое воздействие
.sin)( tBtg
в
(12.1)
Ошибка гармонически линеаризованной нелинейной системы,
которая представляет собой сигнал на входе нелинейного звена,
будет равна
).sin()(
~
tAtx
в
в
(12.2)
В символической форме записи выражениям (12.1) и (12.2)
можно придать вид
,)(
tj
в
Betg
ω
.)(
~
tj
jв
в
eAetx
ω
(12.3)
Пользуясь комплексным коэффициентом гармонической ли-
неаризации нелинейности (10.18), получим для уравнения вынуж-
денного процесса (1.33) в комплексной форме записи
.)(
~
)()()()(
~
0
Г
dtxAKktgtx
вв
(12.4)
Учитывая, что
τω
)(
~
)(
~
в
j
вв
etxtx
, и оставляя под знакомм
интеграла в (12.4) величины, зависящие только от
, получим
),(
~
)()()()(
~
Г
txAKjWtgtx
в
в
в
(12.5)

38 39
При этом возможны два случая:
1) когда кривая
),(
в
AZ
выходит из начала координат и искомая
зависимость )(BAA
существует при любых сколько угодно ма-
лых значениях
B
(рис.12.3,б);
2) когда точка пересечения кривой
),(
в
AZ
существует толькоо
для
B
превышающей некоторое пороговое значение (рис.12.3,в).
При
)(
в
BВ
пор
вынужденные колебания на частоте
в
невозможны. При
)(
в
BВ
пор
возможно существований вынуж-
денных колебаний на частоте
в
. Пороговое значение
)(
в
B
пор
зависит от частоты внешнего воздействия и эта зависи-
мость может бытьнайдена при использовании семейства кривых
),(
в
AZ
по параметру
в
.
Качественный вид зависимости
)(
в
BВ
пор
показан на
рис.12.4. Область существования одночастотного вынужденного
колебания распологается выше показанной кривой.
Если при
0
пор
BВ
, кривые )(
jW и
)(
1
AK
Г
пересека-
ются (рис.11.1), то в системе возможны автоколебания частоты
a
c с амплитудой
a
A
. Этот случай показан на рис.12.4, где при
a
в
имеем
0
пор
B
.
Режим
пор
BВ
, соответствующий вынужденному колебанию
на частоте внешнего, воздействуя
в
, называется режимом при-
нудительной синхронизации или захватыванием. Такое назва-
+j
+1
0
B
B
B
A
A
0
0
а) б)
в)
)(
в
B
пор
пор
B
),(
в
AZ
Рис.12.3.Графический метод
нахождения зависимости
амплитуды вынужденных
колебаний от амплитуды внешнего
гармонического воздействия
При известной частоте ко-
лебаний
в
вынужденных коле-
баний можем на комплексной
плоскости изобразить кри-
вую
),(
в
AZ
, задаваясь различ-
ными значениями амплитуды
A
(рис.12.1). Правую часть урав-
нения изобразим на этой комп-
лексной плоскости окружнос-
тью с заданным радиусом
B
.
Пересечение окружности с
кривой
),(
в
AZ
дает решение
задачи: точка пересечения C по-
зволяет определить фазовый сдвиг и амплитуду
A
(по оцифров-
ке кривой
),(
в
AZ
. Зависимость амплитуды вынужденных коле-
баний можно получить, если изобразить семейство кривых
),(
в
AZ
по параметру
в
(рис.12.2,a).
Таким же путем, строя кривые
),(
в
AZ
по какому-либо па-
раметру
k
, интересующего нас можем найти зависимость
)(kAA
от амплитуды внешнего гармонического воздействия
B
фиксируется семейство окружностей с радиусами
B
(рис.12.3,а ).
+j
+1
0
A
С
B
),(
в
AZ
Рис.12.1.Графическое определение
амплитуды и фазы
вынужденных колебаний
в
ныхпри различ
AZ
)(
а)
Рис.12.2.Графическое определение (а) зависимости амплитуды А
вынужденных колебаний от частоты (б)
и от какого либо параметра k (в)
A
+j
+1
0
в
k
B
A
A
0
0
б)
в)
