Adlard E.R. (ed.) Chromatography in the Petroleum Industry
Подождите немного. Документ загружается.


382
Chapter
I3
trapezoidal rule after the peak boundaries have been located from the first and
second derivatives
[
1,147.
Location of peak boundaries is very sensitive to the
S/N
ratio and if they are
not located accurately, the baseline drawn below the peak will be placed incor-
rectly with consequential errors in area measurement
[
151.
Overlapping peaks, roughly similar
in
size, are separated for measurement by
dropping perpendiculars from the valley points between them.
As
resolution de-
creases, the valley points become harder to locate, and less accurate to use. By
the time a peak becomes a shoulder on another peak, its measurement is grossly
inaccurate.
When one peak is very much smaller than another, it is separated from the
larger peak by skimming a tangent beneath it and its area is measured above the
tangent. This measured area
is
underestimated in two ways: first, by constructing
a straight baseline where the true baseline (the tail of the larger peak) is curved,
and second, by using construction algorithms that depend on the peak’s position
on the tail
[1,16].
13.4.5
Baseline placement
Integrators and computers draw straight lines beneath peaks to simulate base-
line though at least one commercial system has simulated the baseline beneath a
tangent skimmed peak with an exponential fitted curve. The true baseline is the
detector signal in the absence of the measured peak (or peaks) and in tempera-
ture programmed analyses or where the measured peaks are skimmed from an-
other, the true baseline can be highly non-linear.
Where a group of overlapping peaks sit on a curved baseline, integrators place
a baseline beneath the whole group by means of the “elastic band technique”
[l].
If the chromatogram is imagined to be a solid projection up and out
of
the chart,
the baseline constructed beneath a group will be the same shape as a piece
of
elastic, stretched and placed around the underside of the group. This baseline
will touch the beginning and end of the group and some of the lower valleys in a
series of straight lines.
13.4.6
Mathematical separation (deconvolution)
of
peaks and integrator
developments
The mathematical separation of overlapping peaks using peak models has
been attempted since before the first electronic integrators were manufactured,
but,
so
far, without enough success to induce manufacturers to incorporate any

Modern data handling methods
383
of the methods into data processors. The mathematical methodology of separat-
ing peaks falls into
two
broad categories:
1.
selective extraction
2.
resolution enhancement
13.4.7
Selective extraction
13.4.7.
I
Peak
modelling
In modelling, peak shape models (e.g. Gaussian) are assumed and fitted to ex-
posed parts
of
a peak curve in order to allow the whole peak to be defined. This
is
subtracted from the chromatogram envelope and the process repeated with
other peaks until all are removed and only baseline remains. The composition of
the analyte is then calculated from the subtracted peak areas. Many peak models
have been proposed: gaussian, exponentially modified gaussian (EMG), lorent-
zian, log normal and others
[
17-19].
The exponentially modified gaussian is bearing most experimental hit
[20,
2
11.
Some success in deconvoluting simulated overlap of computer generated
EMG peaks has been reported [22], but real chromatograms remain a problem.
13.4.7.2
Signal
subtraction
A
form of selective extraction which does not depend on peak shape
is
the
subtraction
of
two stored signals (chromatograms). This has been adopted into
commercial integrators to remove baseline drift and/or highlight differences
between complex chromatograms. It is a development of the dual
FID
GC
with
two
identical columns to offset baseline drift “on the fly”. It creates purchase
economies because a single column GC can be used where
a
dual column GC
would have been bought; it extends specification because matched columns
could never subtract chromatograms, only baselines.
Two chromatograms are stored: one is the chromatogram with all peaks and
baseline drift, the other is the same chromatogram without sample injection, i.e.
the baseline and drift. Provided that the experimental conditions are stable, the
baseline should be identical in both experiments, and when one data set is sub-
tracted from the other, what remains are the peaks on a flat baseline. Constant
(and unwanted) events such
as
injection pulses or baseline spikes created by
valve switching are also removed.
Differences between complex chromatograms can indicate complex contami-
nation (more than one contaminant peak), or material degradation [22a]. The
difference chromatogram contains the errors of both chromatograms, but then,
so
did matched columns.
References
pp.
398-399

3
84
Chapter
13
13.4.8 Resolution enhancement
In resolution enhancement, peaks variances are reduced until the peaks re-
solve sufficiently to be measured. Numerical techniques such as Fourier trans-
form and others have been used
[
10,23-261.
These approaches have generally disappointed because:
(i)
There is not enough information in an
FID
or other single channel detec-
tor. With perfect deconvolution, a single peak can be resolved into its
components, and if this peak is pure, then deconvolution would count
the isomers, a number which can be checked independently. However,
an identically shaped peak of another species would have to yield an-
other set
of
isomers and a different number. GC
MS
and
GC
FTIR
offer
more information, as does diode array detection but
so
far this is limited
to
LC.
The next challenge to the mathematical resolution of overlapping
peaks can be expected to come
from
multichannel detectors coupled to
computers powerful enough to untangle the data.
(ij)
Both the extraction and resolution approaches to peak separation assume
that peak shape is constant even if it does not conform to a specific
model. The quality of manufacture
of
chromatographs and columns is
not yet good enough to uphold this assumption. Repeated injections
of
the same solute rarely produce identical chromatograms, but the
situa-
tion is improving: Ghaoui has reported the successful improvement of
S/
N
ratio without significant peak broadening by ensemble averaging [27].
(iii) Much of the methodology for peak separation is adapted from spectros-
copy. When applied to chromatography and variously asymmetric peaks,
some methods have been shown to generate spurious peaks and to distort
peak shape further
[
12,131.
Over the years, resolution enhancement
has
been more successful than peak
modelling but the major improvement in resolution has been the introduction of
capillary columns, not better mathematics.
Until such time as all variables affecting peak shape and signahoise ratio are
brought under control, mathematical techniques will be successfully applied only
in limited circumstances, and integrator peak separation techniques will stay at
the perpendicular/tangent level.
13.5
MEASUREMENT
ERRORS
13.5.1
Accuracy
and
precision
Integrators are very good at delivering repeatable results if the instrument

Modern data handling methods
385
conditions are stable; unfortunately, these results might be totally wrong. This
highlights the difference between precision and accuracy.
Accuracy is how close results are
to
the “right” answer. This is what the ana-
lyst seeks, but if it is to be checked, the right answer must be known in advance
by some wholly independent means or it must have been predicted by theory.
Precision is a measure of how close experimental results are to each other and
they reflect experimental stability and control.
The difference between the “right” answer and the measured answer is called
bias, and bias is never revealed experimentally except when
two
sets of re-
sults relating to the same sample are in complete conflict and one has to be
wrong.
Imprecision is easily observed and measured
as
coefficient of variation
(CV)
or relative standard deviation
(RSD.
Inaccuracy is observed only when there is a
good theoretical model
to
provide the correct value for comparison,
13.5.2
Errors
created
by
noise
Noise determines the smallest quantity of solute that can be detected
[5].
The
minimum detectable quantity is the smallest that can be clearly distinguished
from the background noise.
Noise creates errors around the base of measurable peaks by obscuring the
beginning and end of the peak making it difficult to judge where the baseline
should be drawn. It causes integrators to find valleys at the
start
and end of
peaks, delaying the real start of measurement and tripping end of peak measure-
ment too early. Area is lost. Noise valleys on top of peaks split the area meas-
urements
so
that several peaks are reported, with retention times within seconds
of each other.
Fig.
13.4.
Noise causes premature termination
of
peak measurement
and
area
loss
from
tail.
References
pp.
398-399

3
86
Chapter
13
13.5.3 Errors created by peak overlap
Overlapping peaks are separated by perpendiculars dropped from the valleys
between them to the baseline constructed below them,
or
by tangent skimming
depending on the relative peak sizes. These methods are
known
to be inaccurate
except in limited circumstances
[28,29].
In the absence of better methods, inte-
grators and data processors continue to use them.
Perpendicular separation
of
two peaks
is
only accurate when both peaks are
the same size and shape and have equal response factors. When their response
factors are dissimilar, the valley height should be no more than about
5%
of the
smaller peak height.
If one peak
is
larger than the other, perpendicular separation at the valley will
overestimate the smaller peak and underestimate the larger one. In other words,
the
true cleavage point
is
not the valley bottom but some unidentifiable point up
the side
of
the smaller peak.
Tangent skimming
is
used to separate peaks when the relative peak heights
are about
10:
1
[
181.
There is no theoretical justification for this transition point
[28]
and some manufacturers offer a choice of size ratios. It
is
not only arbitrary,
it creates a discontinuity where the integrator switches from perpendicular to
tangent.
As
a result there can be large changes in measured area for small
changes in peak size.
13.5.4 Errors created by asymmetry
In
itself, asymmetry is not a problem for integrators
[
11.
Integrators measure
peak areas by the trapezoidal rule which makes no assumptions about shape. In
theory a highly asymmetric peak on a flat, noise-free baseline is measured with
the same accuracy as a symmetrical peak.
The problems caused by asymmetry are that it compounds and increases the
errors of noise and overlap, and that it is not a constant phenomenon but can
vary with peak size and ftom peak to peak within the same chromatogram.
Varying asymmetry continually frustrates peak modelling.
Tailing on a noisy baseline causes the integrator to terminate peak meas-
urement early as the tail disappears and becomes indistinguishable from the
noise
[30].
Asymmetry occurs mostly at the base of peaks. It spreads peak bases and in-
creases the overlap between neighbouring peaks. Perpendicular separation of
asymmetrical peaks does not account for the unequal contribution of each peak
to
the other.

Modern data handling methods
387
Variable asymmetry invalidates comparisons of peak height within the same
chromatogram unless careful calibration has been made. If all peaks were the
same shape and varied only in size, overlap correction factors could be success-
fully applied to areas and height would be a simpler measure of quantity.
13.5.5
Transmission
of
systematic errors through large peak groups
Overlap and asymmetry can conspire to create systematic errors which
transmit themselves through the group, creating large measurement errors in un-
expected places [3
11.
The errors created by the use of perpendicular separation of
two
overlapping
peaks are observed in the individual peak measurements but not in the total
measured area of the pair. This is because the area lost from one peak is trans-
ferred to the peak on the other side of the perpendicular. The loss from one is
equal to and cancels the gain in the other, or the sum of the
two
errors is zero. In
general, the sum of the errors,
ei,
in a group of
n
peaks caused by perpendicular
separation is equal to zero:
Ce,
=O
n
(13.1)
alternatively, the error in any one peak measurement,
ep,
is equal, and opposite in
sign, to the sum of the errors in all the other peaks in the group:
(13.2)
n-1
In large groups of peaks such as are common in the WCOT analysis of petro-
leum samples, the errors, even if individually small, can accumulate into a con-
siderable error. The implication of Eq. (13.2) is that there is little credibility in
the measured area of any single peak if it is part of a large group. It is therefore a
priority of method development to break up large groups of peaks into smaller
groups if they contain peaks of specific interest.
Asymmetry predominantly occurs as peak tailing rather than fronting. This
produces a systematic trend in the measurement errors; area is predominantly
transferred to the next peak on the tail. The last peak in the group has no peak on
its tail to receive the transferred error and must therefore accumulate all the sys-
tematic errors of tailing/overlap if Eq. (13.1) is to hold true.
As
a result, where
there are large groups of overlapping and asymmetric peaks, the error in the last
peak area measurement is very large.
References
pp.
398-399
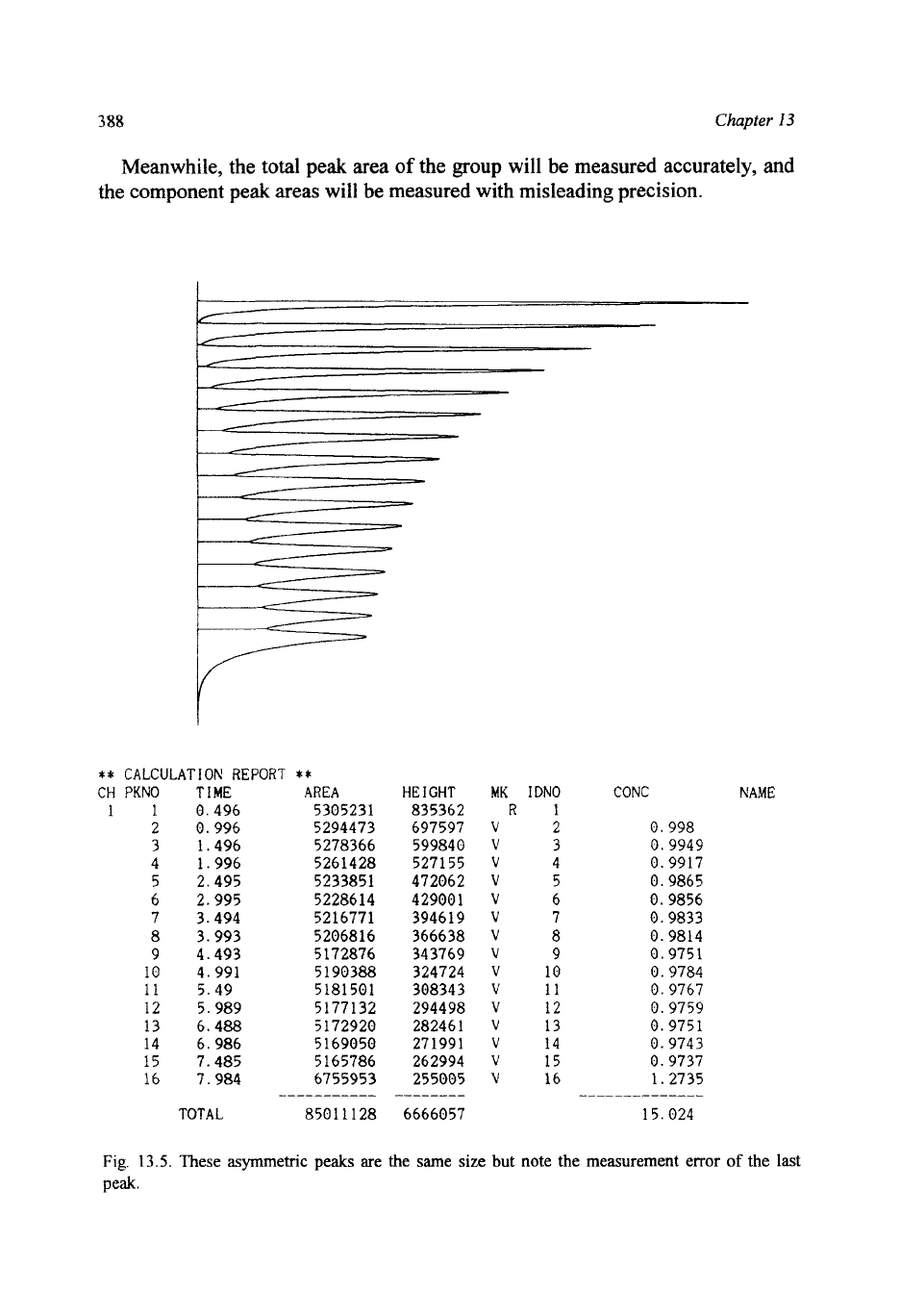
388
Chapter
13
Meanwhile, the total peak area
of
the group will be measured accurately, and
the component peak areas will be measured with misleading precision.
**
CALCULATION
REPORT
**
CH
PKNO
11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
TIME
0.496
0.996
1.496
1.996
2.495
2.995
3.494
3.993
4.493
4.991
5.49
5.989
6.488
6.986
7.485
7.984
TOTAL
AREA
5305231
5294473
5278366
5261428
5233851
5228614
52 1677
1
5206816
5 172876
5 190388
5 181 50
1
5177132
5172920
5 169050
5
165786
6755953
8501 11 28
.
_ __
_______
HE
I
GHT
835362
697597
599840
527155
472062
42900
1
394619
366638
343769
324724
308343
294498
28246
1
271991
262994
255005
6666057
-___
___
_
MK
IDNO
R1
V
2
V
3
V
4
V
5
V
6
V
7
V
8
V
9
v
10
v
11
v
12
V
13
V
14
V
15
V
16
CONC KAME
0.998
0.9949
0.9917
0.9865
0.9856
0.9833
0.9814
0.9751
0.9784
0.9767
0.9759
0.9751
0.9743
0.9737
1.2735
.
-__
-
--
---
-
15.024
Fig,
13.5.
These asymmetric peaks are the same size but note the measurement error
of
the
last
peak.
Modern data handling methods
30
1
25
20
z
15
w
m
:
10
Y
0
a
5
0
Sum
of
Area Measurement Errors
=
0
389
-5
J
12
3
4
5 6
7
8
9
10111213141516
Peak Number
in
Group
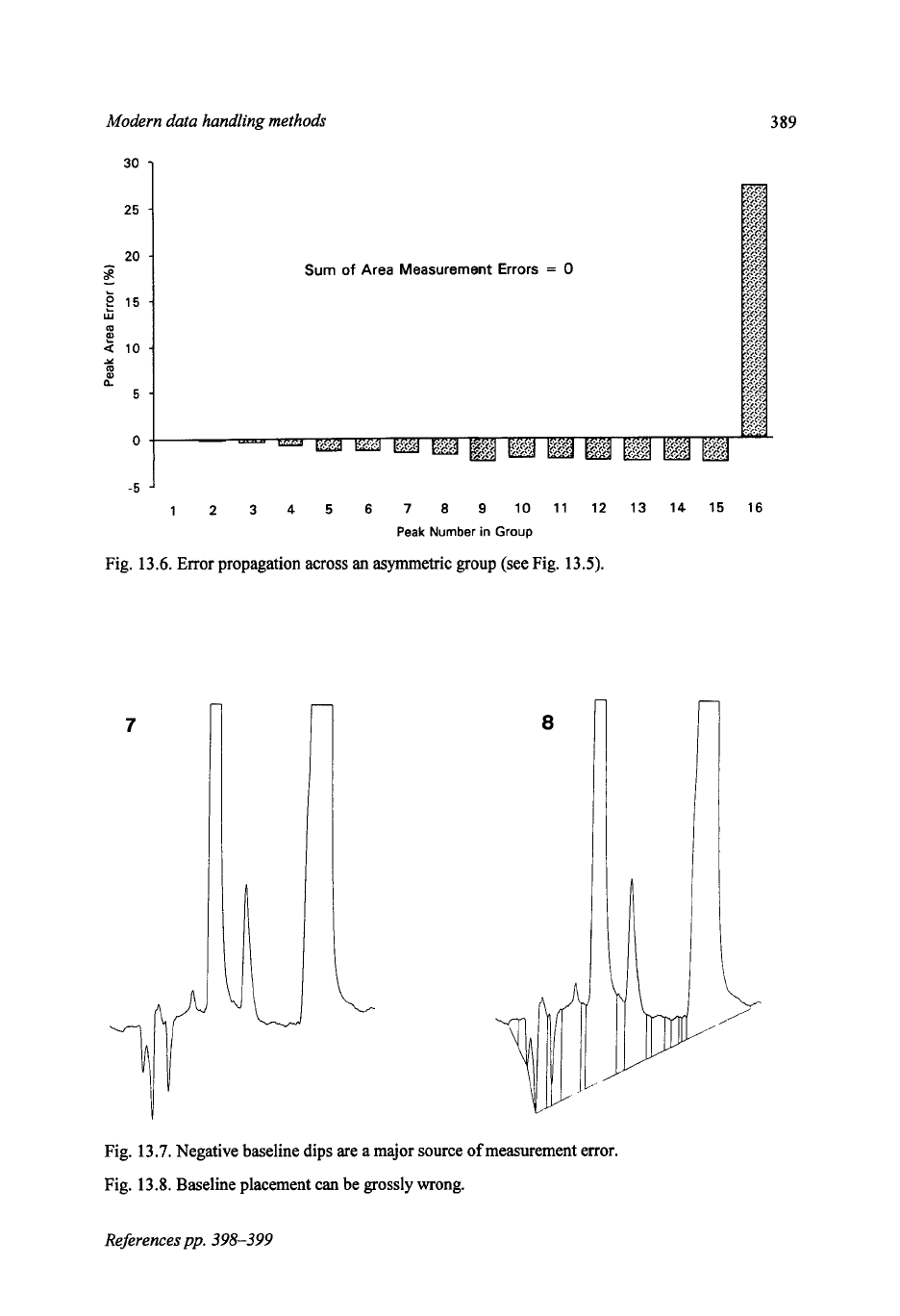
Fig.
13.6.
Error propagation across
an
asymmetric group (see Fig.
13.5).
7
a
Fig.
13.7.
Negative baseline dips are a major source
of
measurement error.
Fig.
13.8.
Baseline placement
can
be grossly wrong.
References
pp.
398-399

3
90
Chapter
13
13.5.6 Baseline construction errors
Baseline construction errors fall into
two
categories:
(i) where the integrator constructs
a
linear baseline even though the true
baseline, i.e. the detector signal in the absence of peaks, is non-linear;
(ii)
where detector signal disturbances, especially those which give negative
dips to the baseline, cause the integrator to draw a baseline in the wrong
place.
Baseline disturbances, especially those involving deep negative dips, can give
rise to enormous errors, especially when the integrator drops perpendiculars to
separate peaks instead of using a tangent skim.
13.5.7 Errors of tangent/perpendicular peak splitting
The criteria for perpendicular and tangent peak separation depend on peak
size, shape and resolution. Different manufacturer's integrators and computers
use different algorithms and measure the same overlapping peaks in different
ways
[32,33].
The measured area of a tangent peak depends on its position on the tail of the
larger peak
[16].
Studies with synthetic chromatograms have shown that there
can be more than
25%
difference
in
the measured area
of
a tangent peak half
way up the side of a peak compared to the same peak located at the end of the
peak's tail
[3
11.
13.5.8 Ease
of
use
The very precise results reported by integrators can mislead the analyst into
believing they are accurate; however, integrators and computers are
so conven-
ient to use and have such a high output of work that they cannot be discarded;
there
is
nothing to replace them.
13.6
CALIBRATION
13.6.1 Use
of
area or height for quantitation
Solute quantity is proportional to peak area
[
11.
Height
is
a single, substitute
measurement for area that wastes most
of
the peak information and assumes
peak shape does not change from one analysis to the next. The choice between
area and height weighs experiment noise levels against peak shape.

Modern data handling methoh
391
Integrators are primarily area measuring devices
[34].
If instrument time con-
stants are too large or the data sampling frequency is not high enough for the
peaks being measured, peak shape is distorted, and peak height changes but not
area. Peak asymmetry may increase as the column ages in use, in these cases
area is the more reliable measure.
Detector non-linearity affects the top of peaks where they are narrowest and
therefore height more than area. Moreover, the linear dynamic range for height
measurements is less than for area measurements
[35,36],
therefore area is pre-
ferred to height if detector linearity is in question.
If the signalhoke ratio is poor
(<25:
1
approx.), noise will obscure the begin-
ning and end of a peak, making baseline placement erratic. Uncertainty at the
base of the peak, the broadest part, is where it matters most and creates the
greatest area error.
A
gain or loss of
2%
at the base
of
a peak will result in a gain
or loss
of
5%
to its area
[15].
Height is therefore more accurate and becomes the
preferred measure with noisy chromatograms.
13.6.2
Calculations and response factors
The three standard calculations of chromatography are:
-
area
%
or normalization
-
internal standard
-
external standard
These days further processing of results is possible by exporting them into
computer spreadsheet files and special maths packages where they can be
worked endlessly into new reports or used to monitor trends. These are too nu-
merous to include here but they do conserve the analyst's time. It is important
to remember that the quality of these sophisticated methods is entirely depen-
dent on, and no better than, the original accuracy and precision of the measured
areas.
13.6.3
Limitations of the standard calculations
13.6.3.
I
Area
%
The concentration of a solute,
ci,
is given by
A;
Ri
c.
=-
x
100%
'
EAjRj
(13.3)
where
Ai
is the peak area of solute
i,
Ri
is the absolute response factor of solute
i,
defined as the quantity of solute to produce a peak of unit area.
References
pp.
398-399
