Accardi L., Freudenberg W., Obya M. (Eds.) Quantum Bio-informatics IV: From Quantum Information to Bio-informatics
Подождите немного. Документ загружается.


This page intentionally left blankThis page intentionally left blank

Quantum
Bio-Informatics
IV
eds. L.
Accardi,
W.
Freudenberg
and
M.
Ohya
© 2011
World
Scientific
Publishing
Co.
(pp.
101-115)
SELF-COLLAPSES
OF
QUANTUM
SYSTEMS
AND
BRAIN
ACTIVITIES
K.-H.
FICHTNER
Unversity
lena,
Institute
of
Applied Mathematics, 01143
lena,
Germany
E-mail: fichtner@mathematik.uni-jena.de
L.
FICHTNER
Unversity
lena,
Institute
of
Psychology, 01143
lena,
Germany
E-Mail: lars.fichtner@uni-jena.de
w.
FREUDENBERG
Techn. University Cottbus, Dep.
of
Mathematics, 03013 Cottbus,
Germany
E-mail: freudenberg@math.tu-cottbus.de
M.OHYA
Department
of
Information
Science and
Quantum
Bio-Informatic
Center,
Tokyo University
of
Science, Noda City, Chiba 218-8510,
lapan
E-Mail: ohya@rs.noda.tus.ac.jp
We
explain
the
relation
between
the
quantum
statistical
model
of
the
recognition
process
developed
in
the
last
years
in
a series
of
papers
(cf.
[7,
9, 10, 11, 12])
and
a
certain
process
of
self-collapses.
This
process
will
be
modeled
by
a classical
homogenous
Markov
chain.
1.
Introduction
Physicists
as
R.
Penrose
or
H. P.
Stapp
(cf.
[25,
38, 39])
but
also
at
an
increasing
rate
specialists of
modern
brain
research (cf. [35, 36, 34, 37])
are
convinced
that
information
processing
in
the
brain
cannot
be
described
appropriately
by
models
based
on
classical physics
or
classical stochastics.
So for
instance
H.
P.
Stapp
argues
in
[38]
that
"classical physics cannot
explain consciousness because
it
cannot explain how the whole can
be
more
than the part.
"
A first
attempt
to
explain
the
process
of
recognition
in
terms
of
quantum
statistics
was given in
[7].
The
procedure
ofrecognition
can
be
described as
101

102
follows:
There
is a
set
of
complex
signals
stored
in
the
memory.
Choosing
one
of
these
signals
may
be
interpreted
as
generating
a
hypothesis
concern-
ing
an
"expected
view of
the
world".
Then
the
brain
compares
a signal
arising from
our
senses
with
the
signal chosen from
the
memory
leading
to
a change
of
the
state
of
both
signals.
Furthermore,
measurements
of
that
procedure
like
EEG
or
MEG
are
based
on
the
fact
that
recognition
of
signals causes a
certain
loss
of
excited
neurons,
i.e.
the
neurons
change
their
state
from excited
to
non-excited.
As
it
was
pointed
out
by
R.
Pen-
rose
[25]
this
change
that
comes along
with
recognition of a signal
can
be
identified
with
a process
of
self-collapses. A
quantum
statistical
model
of
the
recognition process
should
reflect
the
change
of
the
signals
and
the
loss
of
excited
neurons.
In
a (still
incomplete)
series of
papers
the
procedures
of
creation
of
signals from
the
memory, amplification,
accumulation
and
transformation
of
input
signals,
and
measurements
like
EEG
and
MEG
are
treated
in
detail
(cf.
[17,
8, 9, 10, 11, 12, 14, 13, 22]).
In
the
present
note
we will
not
present
this
approach
in
detail
and
in full
mathematical
strength.
A few
of
the
basic ideas
and
structures
of
the
proposed
model
of
the
recognition process will
be
sketched
and
we will
explain
the
relation
between
this
model
and
a
certain
process
of
self-collapses.
In
Section 2 we will collect
some
biological facts
and
experiments
described
in
[26].
Moreover, we will
cite
some opinions given
by
R.
Penrose,
W.
Singer
and
others
allowing
to
formulate
some basic
postulates
and
requirements
each
brain
model
has
to
fulfill.
Our
model
seems
to
be
appropriate
and
in
accordance
with
the
experimental
results.
The
subsequent
section
contains
the
basic
mathematical
notions.
We
introduce
the
underlying
Hilbert
space
representing
the
space
of signals
and
the
basic
operators
acting
on
the
signal
space.
In
the
sequel we
explain
the
basic
ingredients
of
our
model
of
the
recognition process. For simplicity we will
restrict
our
considerations
to
the
case
of
interaction
of
two signals one
coming
from
our
senses
and
the
other
one
created
from
our
memory.
In
Section 4
the
single
steps
of
the
process
of recognition will
be
modelled
by
a
Markov
chain
with
discrete
time.
2.
Some
biological
facts
and
experiments
In
this
section
we
want
to
present
some biological facts
and
experiments.
Each
mathematical
model
describing
certain
aspects
of
brain
activities
should
be
in
accordance
with
these
experimentally
proven facts. Firstly,
using
EEG
measurements
one
gets
information
on
the
densities of
excited
neurons
located
in
the
regions
of
the
brain.
These
densities
depend
on
time.
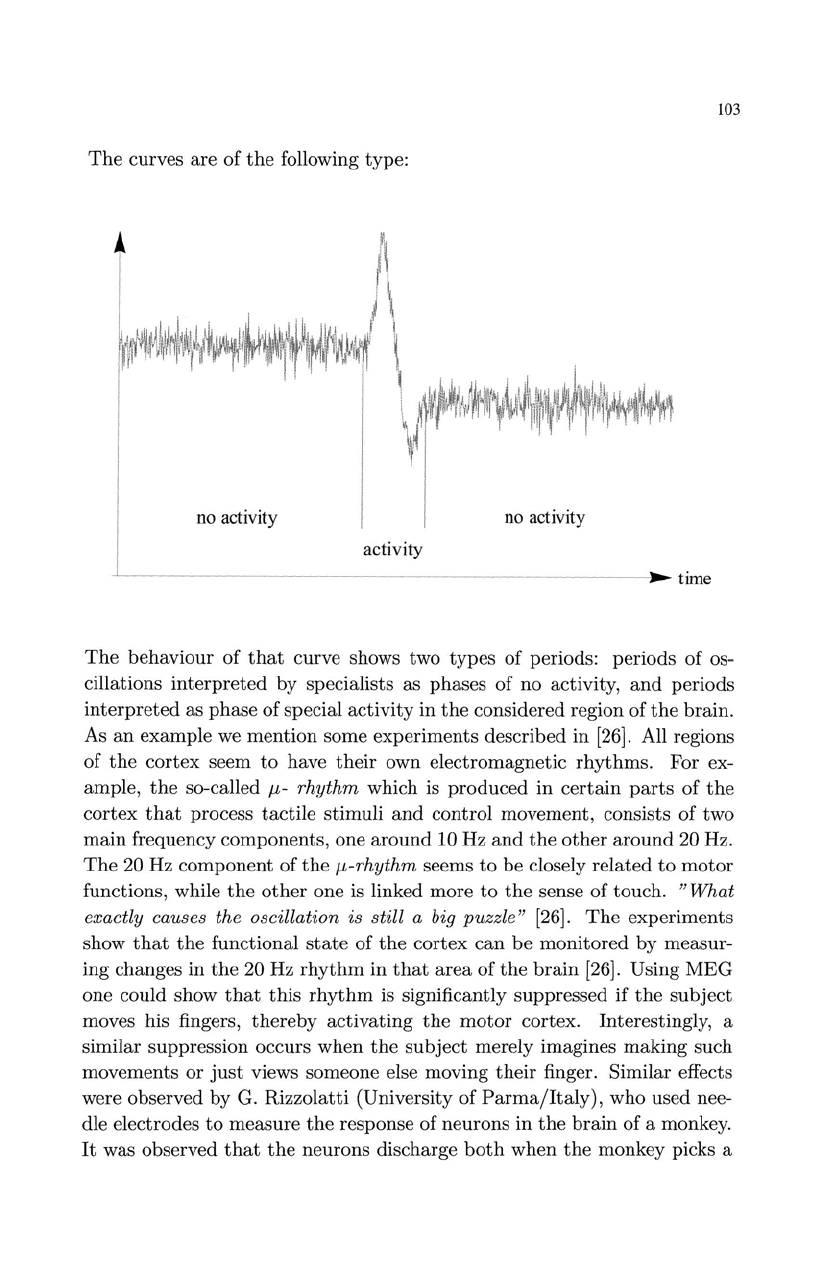
103
The
curves are of
the
following type:
no activity
no activity
activity
...
time
The
behaviour
of
that
curve shows two
types
of
periods:
periods
of
os-
cillations
interpreted
by
specialists as phases
of
no
activity,
and
periods
interpreted
as
phase
of
special
activity
in
the
considered region
of
the
brain.
As
an
example
we
mention
some
experiments
described
in
[26].
All regions
of
the
cortex
seem
to
have
their
own electromagnetic
rhythms.
For
ex-
ample,
the
so-called
p.,-
rhythm
which is
produced
in
certain
parts
of
the
cortex
that
process
tactile
stimuli
and
control movement, consists of two
main
frequency
components,
one
around
10 Hz
and
the
other
around
20 Hz.
The
20 Hz
component
of
the
p.,-rhythm seems
to
be
closely
related
to
motor
functions, while
the
other
one
is linked
more
to
the
sense
of
touch.
"What
exactly causes the oscillation is still a
big
puzzle"
[26].
The
experiments
show
that
the
functional
state
of
the
cortex
can
be
monitored
by
measur-
ing changes in
the
20 Hz
rhythm
in
that
area
of
the
brain
[26].
Using
MEG
one could show
that
this
rhythm
is significantly
suppressed
if
the
subject
moves his fingers,
thereby
activating
the
motor
cortex. Interestingly, a
similar suppression occurs
when
the
subject
merely imagines
making
such
movements
or
just
views someone else moving
their
finger. Similar effects
were observed
by
G. Rizzolatti (University of
Parma/Italy),
who used nee-
dle electrodes
to
measure
the
response of
neurons
in
the
brain
of
a monkey.
It
was observed
that
the
neurons
discharge
both
when
the
monkey picks a

104
raisin
and
when
it
sees
the
experimenter
make
the
same
movement.
The
conclusion is
that
on
e has
to
unravel
the
significance (or
unimportance)
of
the
cortical
rhythms
during
the
periods
of
recognition of signals
or
other
actions
of
the
brain. Summarizing one
can
state
that
there
are
periods
of
no
activity
in
certain
regions
indicated
by
the
rhythms
mentioned above,
and
there
are
periods
of
action
where
the
rhythms
are
suppressed.
Considering a
quantum
model
of
the
brain
the
periods
of
no
activity
in
certain
regions of
the
brain
should
be
represented by a
unitary
evolution
(the
quantum
system
resp. a
part
of
the
system
remains isolated from
the
enviroment),
i.
e.
it
is a process
of
type 2
in
th
e sense
of
J. v.
Neumann
[40].
Now, if
there
will
be
a signal arising from
the
senses
the
process
of
recognition
starts.
That
process represents a
rapid
sequence
of
"trials"
checking
whether
the
signal from
the
senses
and
the
signal
created
by
the
brain
(at
least
partially)
coincide. Let us mention still
Stapp
(cf.
[39])
who
uses
the
second
quantization
of
harmonic
oscillators
to
explain
th
e observed
oscillations.
Stapp
identifies
these
trials
with
measurements performed by
a mysterious
"observer"
in
the
brain
what
seems
to
be
non-realistic.
In
our
model
of
recognition
these
trials
are
not
represented by a process of
measurements. Nevertheless,
the
results of
the
trials
are
represented by
projections like in
the
case of measurements. Now,
the
experimentally
verified
quantum Zeno effect tells us
that
a
rapid
repetition
of
a
certain
measurement
will suppress
the
unitary
evolution
of
the
system
,
i.
e.
the
effects
of
the
measurements
dominate
the
evolution
of
the
system. We will
see
that
the
quantum
model
proposed
by us enables one
to
explain
the
dif-
ferent phases
of
the
curves
obtained
as
the
outcomes
of
EEG
measurements
using
the
quantum
Zeno effect.
Hameroff
and
Penrose discuss in
[25]
the
concept of
quantum
theory
related
to
some biological aspects of
brain
activities. Especially,
they
deal
with
the
problem how recognition
of
signals is connected
with
a process
of
self-
collapses. We would like
to
mention
some basic
statements
taken
from
their
paper
[25]:
-
As
long as a quantum
system
remains isolated from its enviroment,
it
can
be
satisfactorily described
in
terms
of
a deterministic, unitarily evolving
process. That process is computable, non-random, and reversible.
- The conventional quantum theory view is that the quantum state reduces
by
enviroment entanglement, measurement or observation (subjective re-
duction). The
mesurement
process is non-computable, random, and irre-
versible, and
it
is known
in
various contexs as collapse
of
the wave func-
tion.

105
- A number
of
physicists have argued
in
support
of
special models
in
which
the rules
of
standard quantum mechanics are modified
by
the inclusion
of
some additional procedure according to which the reduction
of
the state
be-
comes an objectively real process (objective reduction) the
system
abruptly
self-collapses. That would give a new non-computable theory,
i.
e.
they are
convinced that processes
of
self-collapses cannot
be
described in terms
of
the
conventional quantum mechanics
it
requires additional postulates (relations
to
Gadel's incompleteness theorem ?)
- Consciousness,
it
is argued, requires non-computability. The only read-
ily available apparent source
of
non-computability are self-collapses. The
self-collapse, irreversible in time, creates an instantanoues
"now" event.
Sequences
of
such events create a flow
of
time, and consciousness.
As
it
was
mentioned
in Section 1 in a series of
papers
we developed a
quan-
tum
statistical
model
describing
certain
aspects
of
the
recognition process.
In
the
sequel
we
will
present
now
certain
aspects
of
this
model. We will
argue
that
the
model
is in accordance
with
the
experimental
results
and
the
opinions
cited
above.
The
paper
is focussed
on
the
relation
between
the
process
of
recognition
and
a
certain
process
of
self-collapses.
3.
The
Space
of
Signals
In
the
present
section we
introduce
briefly
notions
and
notations
needed
in
the
sequel.
For
interpretation
and
motivation
of
the
introduced
notions
we refer
to
the
above
mentioned
papers.
Starting
point
will
be
a set G
representing
the
space where
the
process of recognition
and
processing
of
the
signals
takes
place.
For
the
mathematical
model
it
is irrelevant
what
is
the
concrete
structure
of G. So let G
be
an
arbitrary
complete
separable
metric
space
equipped
with
a fixed finite diffuse
measure
on
the
a-algebra
of Borel
sets
of
G.
The
elements
of
the
Hilbert
space
L2
(G,
fJ)
can
be
interpreted
as
functions
of
the excited neurons. We
assume
that
G decomposes
into
disjoint regions G
I
,
...
, G
n
being responsible for different
tasks.
So L2(G
k
)
represents
the
space of
the
excited
neurons
in
the
region G
k
.
Now, let
r(L2(G))
denote
the
symmetric
Fock space over L2(G):
Incoming signals
are
identified
with
states
on
the
symmetric
Fock space
1{
= r(L2(G)).
Why
do
we choose
this
Fock space as signal space?
The
main
reason is
the
possibility
to
identify
the
Fock space over
L2
(G)
with

106
the
tensor
product
of
the
Fock spaces over L
2
(Gd,
...
,
L2(G
n
):
r(L2(G
l
U
...
U G
n
))
=
r(L2(Gd)0
...
0r(L2(G
n
)).
The
signal decomposes according
to
the
decomposition
of
the
space.
Now, we
assume
that
the
decomposition
is fixed
and
maximal (very fine) in
that
sense
that
each
region G
r
is responsible
only
for one simple
task
repre-
sented
by
an
r E
L2(G
r
),
Ilrll = 1,
r::;
n.
For
each
r E
{I,
...
,n},
k
~
1
define functions
fl
E
r(L2(G
r
))
by
r-
{VkT.fIr(Xj),X=(Xl,
...
,Xk)EG
k
,
r-
_
fk
(x)
:=
]=1
,
fo
(x)
:=
1I0(X),
o elsewhere
Observe
that
for
each
r E
{I,
...
,
n}
UIh'2o
gives
an
orthonormal
system
in
r(L2(G
r
)).
We
denote
by
H~ig
c
r(L2(G
r
))
the
Hilbert
space
with
basis
UIh'2o
and
interpret
this
space
as space
of
signals
of
type r.
An
especially
important
class
of
functions
in
the
Fock
space
are
the
so-called exponential
vectors. Exponential vectors
in
H~ig
are
given
by
00
k
exp{a·
r}
= L
~fI
k=O
v
k!
(a
E C).
Observe
that
and
d
m
exp{t·
fr}
I =
~
.
fr
m >
O.
dtm
t=O
m'
One
easily concludes
that
the
linear
span
of
the
exponential
vectors
is dense
in
H~ig,
i.
e.
H~ig
=
Lin{exp{a·
tr}:
a E
IC},
r E {I,
...
, n}.
The
space
'1.Isig . = '1.I
si
g,o,
,o,'1.I
si
g
IL
.
ILl
'U
••.
'U1Ln
(1)
we will call
the
space
of
regular signals.
States
on
Hsig
are
called regular
signals.
The
states
Wg
:=
e-llgl12
.
(exp{g},·
exp{g})
are
called coherent states
on
H~ig
if g E
L2(G
r
)
resp.
on
Hsig
if
g E
L2(G).
Hereby,
(,.)
denotes
the
scalar
product
in
the
corresponding
Hilbert
space.
Roughly
speaking,
coherent
states
describe
states
of
systems
of
quantum
particles
where
each
particle
is in
the
same
one-particle
state.
Furthermore,
Wo
= (exp{O}, . exp{O}) is called
the
vacuum state.

J07
4.
The
Process
of
Recognition
The
recognition process is based
on
a comparison of signals: one signal will
be
the
input
signal coming from
our
senses,
the
other
one is
taken
from
the
memory.
Both
signals
are
modeled by
the
Hilbert space Hsig
introduced
above.
The
memory
spac
e
Hmem
is a
further
Hilbert
space
the
structure
of
which we will
not
discuss in
the
present
paper.
Also we will
not
describe
here
the
mechanism how
the
signal is
taken
out
from memory. A de
tailed
discussion
and
interpretation
one
can
find in
[7]
and
[8,
14, 15].
The
whole
processing
procedure
will take place
step
by
step
on
the
space
The
comparison procedure between
th
e two
mentioned
signals is done
with
the
aid
of
operators
(projections)
on
H
:=
Hsig®Hs
ig
,
and
we
concentrate
our
considerations
to
these first two spaces
of
the
tensor
product
space.
Basic for
our
considerations will
be
the
symmetric
be
am
splitter being a
well-known
operator
in
quantum
optics describing
the
splitting
of
coherent
light
into
two beams.
Definition
4.1.
Let r E
{I,
...
,n}
be
fixed.
The
lin
ea
r
operator
Vr(exp{f}®exp{g})
:=
exp
{~.
(j
+
g)}
®exp
{~.
(j
-
g)}
(2)
we
call
symmetric
beam splitter in
the
region r.
It
is well-known
that
tensor
products
of
exponential vectors
are
total
in
r(L2(G
r
))
®
r(L2(G
r
)).
So
the
symmetric
beam
splitter
Vr
is fully charac-
terized by formula (2).
Proposition
4.1.
(Properties
of
the
symmetric
beam splitter) For r E
{I,
...
,n}
the
symmetric
beam splitter
Vr
is
unitary
and self-adjoint:
V;
=
Vr
and
V;
=
][r(£2(G
r
))0
r(L2(G
r
))
(][
denoting the identical opera-

108
tor). Moreover,
jor
all
j,
g E L2(G
r
)
and
a,
(3
E C
{
a+(3}
{a-(3}
V
r
(exp{aj}0exp{(3j})
=
exp
v'2
j
0exp
v'2
j
V
r
(exp{j}0exp{j})
= exp{
v2j}0exp{O}
1 1
Vr(exp{
O}0exp{j})
= exp{
v'2
j}0exp{
-
v'2
j}
1 1
V
r
(exp{j}0exp{
O})
= ex
p
{v'2
j}0ex
p
{v'2
j}
V;
(exp{J}0exp{g}
) =
exp{J}0exp{g}.
(3)
(4)
(5)
(6)
(7)
A good survey
on
properties
of
general (usually non-selfadjoint)
beam
split-
ting
operators
with
an
arbitrary
number
of
in-
and
outputs
is given
in
[24].
In
the
sequel
Prw
:=
(\{f,
.)\{f
denotes
the
projection
onto
(the
subspace
generated
by) \{f. For r E
{I,
...
,
n}
define projections
T[, T[,
To, To
on
H~ig0H~ig
by
T[
:=
Vr(1I1t~ig0Prexp{O})Vr,
To
:=
V; =
1I1t~ig01I1t~ig
=:
IT)
To
:=
Vr(Ir
-1I1t~ig0Prexp{O})Vr
=
Ir
-
T[
= Ir -
T[
Observe
that
T[
has
the
property
T[
(exp{ar}0exP{br})
= exp
{~(a
+
b)r}
0exp
{~(a
+
b)r}.
So,
T[
corresponds
to
a
projection
onto
the
subspace
of
H~ig
0
H~ig
with
equal first
and
second factor
of
the
tensor
product.
T[
is
interpreted
as
recognition
in
the
r-th
region whereas
To
=
Ir
-
T[
indicates
that
there
was no recognition
in
the
area
r.
Now we
join
together
these
operators
T[
and
fg
of
partial
recognition
resp.
"no"
recognition in
the
single areas
to
operators
on
the
whole
tensor
product
signal space H
:=
Hsig0Hsig. We
put
n
:=
{O,
I}n =
{E
= (EI,'" ,
En):
Ek
E
{O,
I}, k::;
n}
n
n
'i
'=
to.T
r
(£1
, .
..
,E
n
)·
'6'
Er '
r=l
r=l

109
Because
of
notational
convenience we
hav
e
put
in
th
e above definition
T[
:=
T[
(however
To
=I-
~)
This
assembly of
the
opera
tors in
the
single areas
was possible because
of
Now we
want
to
sketch
the
process
of
recognition.
Starting
point
will
be
a
state
{}o
on
H representing a
pair
of
signals
the
first arisen from
the
senses
the
second one
created
from
the
brain. Now,
there
is chosen a
certain
el-
ement
;Sl
=
(cL
... ,
E~)
E n
indicating
what
happ
ens
in
the
first
step
of
recognition:
-
EX:
= 1 indicates recognition
in
the
k-th
region,
-
EX:
= 0 means
there
is no recognition
in
the
k-th
region.
The
corre
sponding
event will
be
identified
with
the
projection
TCcL
...
,e;).
Like
in
the
case
of
measurements
the
probability
of
the
event
(EL
...
,
E~)
is given by
tr
( (}o .
TCc
i ,
...
,e
;))
where
tr(
·) de
note
the
usual
trace
of
an
operator.
Together
with
th
e proba-
bility
tr({}o
. T
E"
) represe
nting
the
subjective reduction
of
the state
{}
caused
by
the
measurement
according
to
TE"
we
can
consider
the
following
trans-
formation
of
the
state
{}o representing objective reduction caused by
the
self-collapse
indicated
by
;Sl:
K
( )
._
TE'l
{}o
TE"
E'l
(}o
.-
tr({}o
.
TE")
provided
tr({}o
.
TE")
>
O.
So for each given sequence
(EL
...
,
E~)
we get
a channel
mapping
the
initial
state
{}o
into
the
new
state
KE"
({}o)
where
partial
recognition
app
e
ars
in
all regions k
with
EX:
=
1.
Starting
point
for
the
second
step
of
recognition will
be
{}l
:=
K
E"
({}o)
and
a second sequence
;S2
E
n.
Applying
th
e
same
procedure replacing {}o by {}l
the
probability
of
the
event
indicated
by
;S2
will
be
