ACCA F2 Management Accounting - 2010 - Study text

Подождите немного. Документ загружается.

Chapter 15: Limiting factors and linear programming

Required

Identify the quantities of production and sales of each product that would maximise

annual profit.

Paper F2: Management Accounting

346 Go to www.emilewoolfpublishing.com for Q/As, Notes & Study Guides © EWP

Limiting factor decisions: linear programming

 Two or more limiting factors

 Formulating a linear programming problem

 The objective function

 Formulating the constraints

2 Limiting factor decisions: linear programming

2.1 Two or more limiting factors

When there is more than one limiting factor (other than sales demand for the

products), the contribution-maximising plan cannot be identified simply by ranking

products in order of contribution per unit of limiting factor.

For example, suppose that a company makes two products, X and Y, and there are

two limiting factors, labour time and machine time. The contribution per unit of

limiting factor might be as follows:

Product X Product Y

Contribution per labour hour $12 $9 Rank Product X first

Contribution per machine hour $7 $10 Rank Product Y first

In this situation, the products cannot be ranked in order of contribution per unit of

limiting factor because the ranking is different for each limiting factor. The problem

is therefore to decide how to maximise total contribution given two (or more)

limiting factors.

The problem can be formulated as a linear programming problem.

2.2 Formulating a linear programming problem

A linear programming problem is formulated by:

 identifying an objective function, and

 formulating two or more constraints, one for each limiting factor or other

restriction (such as maximum sales demand).

2.3 The objective function

The objective of a linear programming problem is to maximise or minimise the

value of something. For the purpose of your examination, it is likely to be the

objective of maximising total contribution. (The objective might possibly be

something else, such as the objective of minimising costs.)

An objective function expresses the objective, such as total contribution, as a formula.

Chapter 15: Limiting factors and linear programming

Example

A company makes and sells two products, Product X and Product Y. The

contribution per unit is $8 for Product X and $12 for Product Y. The company wishes

to maximise profit.

If it is assumed that total fixed costs are the same at all levels of output and sales, the

objective of the company is to maximise total contribution.

Total contribution can be expressed as a formula, as follows:

Let the number of units (made and sold) of Product X be x

Let the number of units (made and sold) of Product Y be y

The objective function is therefore to maximise:

(Total contribution): 8x + 12y.

2.4 Formulating the constraints

In a linear programming problem, there is a separate constraint for each item that

might put a limitation on the objective function. Maximum sales demand for a

product might be a constraint, as well as a restricted supply of a resource such as

direct labour hours.

For each item that might be a limiting factor, a constraint must be included in the

linear programming problem. There is one constraint for each limiting factor.

Each constraint, like the objective function, is expressed as a formula. Each

constraint must also specify the amount of the limit or constraint.

A constraint is a formula that is not an equation with a equals sign (‘=). It normally

has an ‘equal to or less than’ sign (≤), although a constraint might possibly have an

‘equal to or more than’ sign (≥).

The basic technique for formulating the constraints for resources

To formulate the constraints for a problem, you must identify each item that might

be a limiting factor, such as labour time for a specific grade or type of labour,

machine time for a specific type of machine, the availability of a specific type of

materials, or maximum sales demand for a product.

For each of these possible limiting factors, there must be a separate constraint in the

problem.

The variables in the problem (x and y) are the same as for the objective function.

In a limiting factor problem, it is usual to find that material, labour time or machine

time are constraints.

 Materials. If materials might be a limiting factor, a constraint is formulated as

follows, when there are M units of materials available in total, and one unit of

Paper F2: Management Accounting

348 Go to www.emilewoolfpublishing.com for Q/As, Notes & Study Guides © EWP

Product X needs m

units of the material and one unit of Product Y needs m

units of the material. The constraint is:

x + m

y ≤ M

For example, suppose that each unit of Product X needs 3kg of material and each

unit of Product Y needs 4 kg of the same material, and the total material available

is 6,000 kg, the constraint for materials is:

3x + 4y ≤ 6,000.

 Labour. A grade or type of labour might be a limiting factor. If there are T hours

of the labour time available in total, and one unit of Product X needs t

hours of

the labour time and one unit of Product Y needs t

hours, the constraint is:

x + t

y ≤ T

For example, suppose that each unit of Product X needs 30 minutes of skilled

labour time and each unit of Product Y needs 15 minutes of skilled labour time,

and total skilled labour is restricted to 200 hours per week, the constraint for

skilled labour is:

0.50x + 0.25y ≤ 200.

If you don’t like fractions or decimal figures in a constraint, you can multiply

this constraint by 4 to get rid of the decimals, and the constraint will be:

2x + y ≤ 800.

 Machine time. Machine time might be a limiting factor. If time on a particular

type of machine or equipment might be a limiting factor, there are T hours of the

machine time available in total, and one unit of Product X needs t

hours of the

machine time and one unit of Product Y needs t

hours, the constraint is:

x + t

y ≤ T

Formulating a constraint for machine time is therefore very similar to

formulating constraints for materials or labour time.

Maximum sales demand constraint

If there is a maximum limit, the constraint must be expressed as ‘must be equal to

or less than’.

For example, if there is a maximum sales demand for Product X of 5,000 units, the

constraint for sales demand for X would be expressed as:

x ≤ 5,000

Chapter 15: Limiting factors and linear programming

Minimum sales demand constraint

Similarly, if there is a minimum limit, the constraint must be expressed as ‘must be

equal to or more than’. For example, if there is a requirement to supply a customer

with at least 2,000 units of Product X, this constraint would be expressed as:

x ≥ 2,000

Non-negativity constraints

A requirement of linear programming problems is that there should be no negative

values in the final solution. For example, it is not possible to make and sell minus

4,000 units of Product Y.

Constraints in the linear programming problem should therefore be that each

‘variable’ must be equal to or greater than 0.

For example:

(Non-negativity constraint): x, y ≥ 0.

Example

A company makes and sells two products, Product X and Product Y. The

contribution per unit is $8 for Product X and $12 for Product Y. The company wishes

to maximise profit.

The expected sales demand is for 6,000 units of Product X and 4,000 units of Product

Y. However, there are limitations to the amount of labour time and machine time

that is available in the period:

Product X Product Y

Direct labour hours per unit 3 hours 2 hours

Machine hours per unit 1 hour 2.5 hours

Total

hours

Direct labour hours available, in total 20,000

Machine hours available, in total 12,000

A linear programming problem can be formulated as follows:

Let the number of units (made and sold) of Product X be x

Let the number of units (made and sold) of Product Y be y

The objective function is to maximise total contribution: 8x + 12y.

Subject to the following constraints:

Direct labour 3x + 2y ≤ 20,000

Machine time x + 2.5y ≤ 12,000

Paper F2: Management Accounting

350 Go to www.emilewoolfpublishing.com for Q/As, Notes & Study Guides © EWP

Sales demand, X x ≤ 6,000

Sales demand, Y y ≤ 4,000

Non-negativity x, y ≥ 0

If you do not like figures with fractions in a constraint, the constraint for machine

time could be expressed (by doubling it) as:

Machine time 2x + 5y ≤

24,000

Exercise 2

A company manufactures and sells two models of a product, the Standard model

and the Economy model. The models are made from the same materials, but the

Standard model includes more material than the Economy model. The Standard

model makes a contribution of $6 per unit and the Economy model makes a

contribution of $4 per unit.

Sales demand each year for the Standard model is 20,000 units and for the Economy

model it is 16,000 units.

There are several resources in short supply. The annual availability of materials and

labour are as follows:

Direct materials $105,000

Skilled labour 16,500 hours

Unskilled labour 56,000 hours

The resources required per unit of product are as follows:

Standard Economy

per unit per unit

Direct materials per unit $4.00 $2.50

Skilled labour hours per unit 0.5 hours 0.5 hours

Unskilled labour hours per unit 1.25 hours 2 hours

Required

Formulate a linear programming problem for the maximisation of annual

contribution and profit.

Let the number of units (made and sold) of the Standard model be x

Let the number of units (made and sold) of the Economy model be y.

Chapter 15: Limiting factors and linear programming

Linear programming: graphical solution

 Three-stage graphical method

 Drawing the constraints on a graph

 Maximising (or minimising) the objective function

 Calculating the value for the objective function: simultaneous equations

 An alternative approach to a solution: simultaneous equations

 Linear programming: problems with more than two variables

3 Linear programming: graphical solution

3.1 Three-stage graphical method

When there are just two variables in a linear programming problem (x and y), the

problem can be solved by a graphical method. The solution identifies the values of x

and y that maximise (or minimise) the value of the objective function. A graphical

solution can therefore be used to solve a linear programming problem only when

there are two products, although there might be more than two constraints.

There are three stages in solving a problem by the graphical method:

 Step 1: Draw the constraints on a graph, to establish the feasible combinations of

values for the two variables x and y that are within all the constraints in the

problem.

 Step 2: Identify the combination of values for x and y, within this feasible area,

that maximises (or minimises) the objective function. This is the solution to the

problem.

 Step 3: Calculate the value for the objective function that this solution provides.

3.2 Drawing the constraints on a graph

The constraints in a linear programming problem can be drawn as straight lines on

a graph, provided that there are just two variables in the problem (x and y). One

axis of the graph represents values for one of the variables, and the other axis

represents values for the second variable.

The straight line for each constraint is the boundary edge of the constraint – its outer

limit (or inner limit, in the case of minimum values).

For example, suppose we have a constraint:

2x + 3y ≤ 600

The outer limit of this constraint is represented by a line:

2x + 3y = 600.

Paper F2: Management Accounting

Combinations of values of x and y beyond this line on the graph (with higher values

for x and y) will have a value in excess of 600. These exceed the limit of the

constraint, and so cannot be feasible for a solution to the problem.

The constraint is drawn as a straight line. To draw a straight line on a graph, you

need to plot just two points and join them up. The easiest points to plot are the

combinations of x and y:

 where x = 0, and

 where y = 0.

For the equation 2x + 3y = 600:

 when x = 0, y = 200 (= 600/3). So plot the point x = 0, y = 200 on the graph

 when y = 0, x = 300 (= 600/2). So plot the point y = 0, x = 300 on the graph

Join these two points, and you have a line showing the values of x and y that are the

maximum possible combined values that meet the requirements of the constraint.

Example

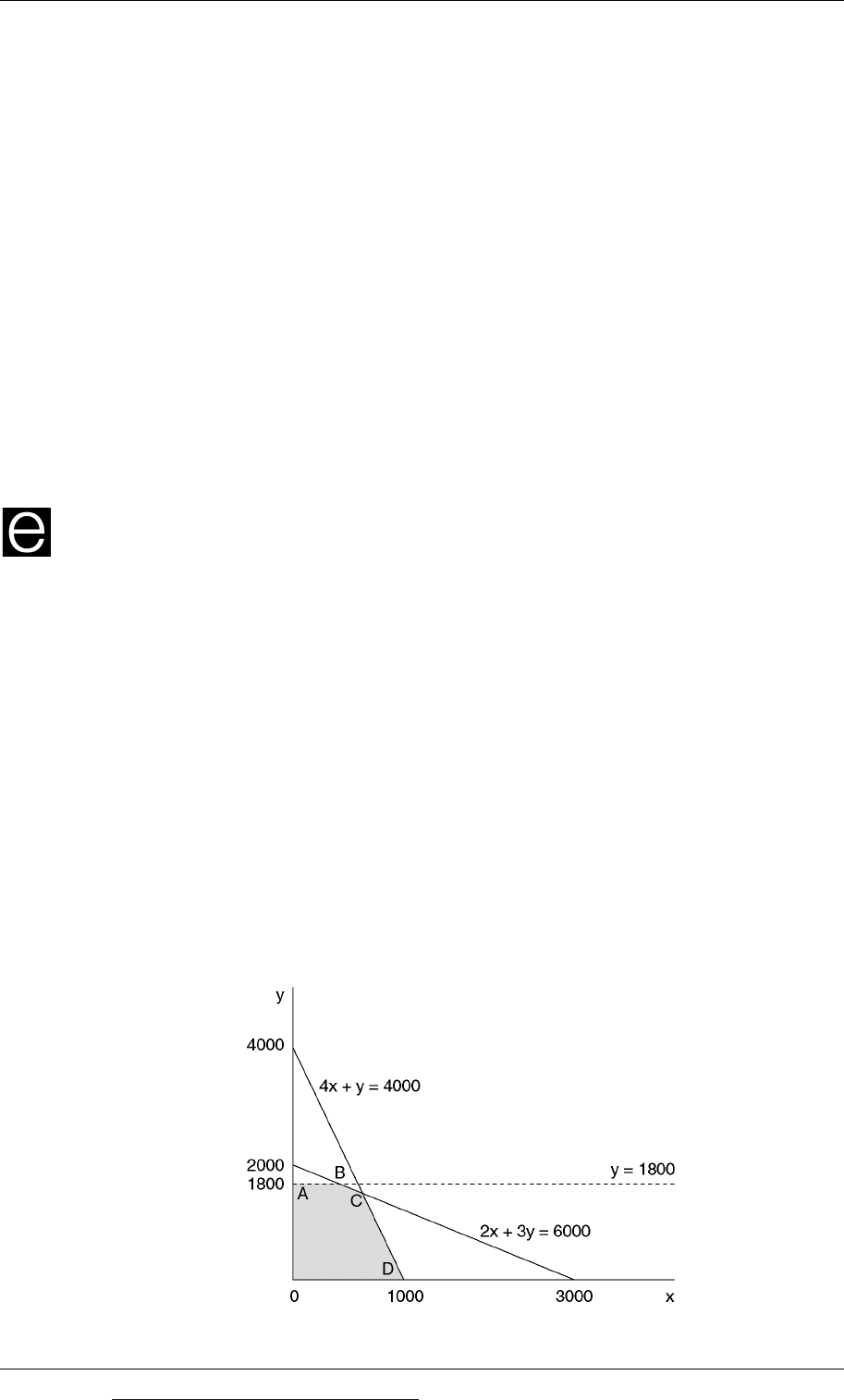
Suppose that we have the following linear programming problem:

The objective function is to maximise total contribution: 5x + 5y

subject to the following constraints:

Direct labour 2x + 3y ≤ 6,000

Machine time 4x + y ≤ 4,000

Sales demand, Y y ≤ 1,800

Non-negativity x, y ≥ 0

The non-negativity constraints are represented by the lines of the x axis and y axis.

The other three constraints are drawn as follows, to produce a combination of

values for x and y that meet all three constraints. These combinations of values for x

and y represent the ‘feasible region’ on the graph for a solution to the problem.

Chapter 15: Limiting factors and linear programming

The feasible area for a solution to the problem is shown as the shaded area OABCD.

To solve the linear programming problem, we now need to identify the feasible

combination of values for x and y that maximises the objective function.

3.3 Maximising (or minimising) the objective function

As a starting point, you might recognise that the combination of values for x and y

that maximises the objective function will be a pair of values that lies somewhere

along the outer edge of the feasible area.

In the graph above, the solution to the problem will normally be the values of x and

y at one of the following points on the graph:

 A

 B

 C, or

 D

In other words, we will normally expect the solution to be the combination of values

for x and y that lies at one of the ‘corners’ of the outer edge of the feasible area.

(In some cases, the solution might be:

 any combination of values of x and y along the line AB, or

 any combination of values of x and y along the line BC, or

 any combination of values of x and y along the line CD.

However, this would be unusual.)

To identify the combination of values for x and y that are feasible (within all the

constraints) and that also maximises the objective function, we need to look at the

objective function itself.

Drawing an iso-contribution line

We do not know the maximum value (or minimum value) of the objective function.

However, we can draw a line that shows all the combinations of x and y that

provide the same total value for the objective function.

For example, suppose that the objective function is to maximise contribution 4x +

3y. We can draw a line on a graph that shows combinations of values for x and y

that give the same total contribution, when x has a contribution of 4 and y has a

contribution of 3. Any total contribution figure can be chosen, but a convenient

multiple of 4 and 3 is simplest and easiest.

 For example, we could select a total contribution value of 4x + 3y = 12,000. This

contribution line could be found by joining the points on the graph x = 0, y =

4,000 and y = 0, x = 3,000.

 Instead, we might select a total contribution value of 4x + 3y = 24,000. This

contribution line could be found by joining the points on the graph x = 0, y =

8,000 and y = 0, x = 6,000.

Paper F2: Management Accounting

If you draw both of these contribution lines on a graph, you will find that:

 the two lines are parallel to each other on the graph, and

 the line with the higher total contribution value for values of x and y (24,000) is

further away from the origin of the graph (where x = 0 and y = 0, i.e. Point 0)).

A contribution line can be used to identify the solution to a linear programming

problem.

 Draw a line showing combinations of values for x and y that give the same total

value for the objective function. (This might be called an ‘iso-contribution’ line –

meaning ‘the same’ contribution: every combination of values on the

contribution line will give the same total contribution.)

 Look at the slope of the contribution line, and (using a ruler if necessary) identify

which combination of values of x and y within the feasible area for the

constraints is furthest away from the origin of the graph. This is the combination

of values for x and y where an iso-contribution line can be drawn as far to the

right as possible that just touches one corner of the feasible area.

This is the combination of values of x and y that provides the solution to the linear

programming problem.

Example: using an iso-contribution line

Returning to the previous example, we can draw an iso-contribution line for, say, 5x

+ 5y = 10,000, by joining the points x = 0, y = 2,000 and y = 0, x = 2,000. (The value

10,000 is chosen here as a convenient multiple of the values 5 and 5.)

The iso-contribution line shows us the slope of all other iso-contribution lines. The

optimal solution to the linear programming problem, when we want to maximise

contribution, is a combination of x and y that:

 is as far away from the origin of the graph as possible, and

 provides a feasible solution to the problem.

This will give us a combination of x any y that provides a maximum value for

contribution, which satisfies all the constraints in the problem.

In this example, the optimal solution lies at point A, point B, point C or point D.

ACCA F2 Management Accounting - 2010 - Study text - Emile Woolf Publishing

Подождите немного. Документ загружается.