Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию

Подождите немного. Документ загружается.

1021. Известна игра на придумывание слов, состоящих из тех

же букв, что и некоторое фиксированное слово - образец. Например, из

слова ПАСКАЛЬ можно получить слова ЛАК, ЛАСКА, СКАЛА и т.д.

Кратные вхождения некоторой буквы в получаемое слово

допускаются, если эта буква с неменьшей кратностью вх одит в слово -

образец. Пу сть дана последовательность слов, разделенных пробелами.

Приняв, что первое слово в последовательности есть образец, выбрать

те из остальных членов последовательности, которые могут быть

получены из образца по указанному выше правилу. Максимально

возможную длину слова считать равной 15.

1022. На квадратном листе клетчатой бумаги размера 8×8

клеток нарисовано несколько прямоугольников, каждый

прямоугольник состоит из клеток, различные прямоугольники не

накладываются друг на друга и не соприкасаются (см. пример на рис.

119). Дана целочисленная квадратная матрица порядка 8, в которой

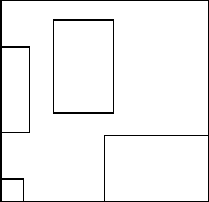
элемент равен 0, если соответствующая клетка принадлежит какому-

либо прямоугольнику, и отличен от нуля в противном случае.

Определить число прямоугольников.

1023. Дана целочисленная матрица

[

]

mjni

,...,1;,...,1 ==

Прямоугольником в этой матрице будем называть множество всех

элементов

a , для которых выполнено ,1,1 msjrnqip ≤≤≤≤≤≤≤≤

где

,,, - натуральные числа, задающие прямоугольник.

Площадью прямоугольника назовем число элементов в нем.

Рис. 119

Среди прямоугольников матрицы, состоящих целиком из нулей, найти

тот, который имеет наибольшую площадь.

1024. Дана целочисленная матрица размера mn × , в которой

имеются ровно два одинаковых элемента. Найти индексы этих

элементов.

1025. Поле шахматной доски задается парой натуральных

чисел: первое у казывает номер вертикали при счете слева направо,

второе - номер горизонтали при счете снизу вверх. Расстановка фигур

задается таким образом, что вначале указываются поля, на которых

стоят перечисленные белые фигуры, затем - поля, на которых стоят

перечисленные черные фигуры.

а) На доске стоят два ферзя. Указать поля, на которые может

пойти белый ферзь так, чтобы не попасть под удар черного ферзя.

б) У белых на доске остался только король, у черных - король,

конь, слон. Охарактеризовать положение белых с помощью слов: мат,

шах, пат, обыкновенная позиция.

1026. «Тестирование коллектива». Пусть целочисленная

матрица размера mn × содержит информацию об учениках некоторого

класса из п человек: j-я строка содержит информацию о i-м ученике. В

первом столбце проставлен возраст в годах, во втором - рост в см, в

третьем - успеваемость (округленный средний балл) и т.д. Ученик

называется среднестатистическим по k-му параметру (уникальным по

k-му параметру), если на нем достигается минимум (максимум) модуля

разности среднего арифметического чисел из k-го столбца и значения

k-го параметра этого ученика. Ученик называется самым уникальным

(самым средним), если он уникален (является среднестатистическим)

по самому большому количеству параметров. По матрице указанного

вида определить номера учеников:

а) самых уникальных;

б) самых средних;

в) самых средних среди самых уникальных;

г) самых уникальных среди самых средних.

1027. Правильное скобочное выражение получается из

некоторого математического выражения, содержащего круглые

скобки, вычеркиванием всех знаков, кроме круглых скобок. Например,

из выражения a - b( c + 2( x + y( z + 1 ))) + a ( c + x ) получается

правильное скобочное выражение ((( ))) ( ). Более точное описание

множества правильных скобочных выражений:

1) ( ) - правильное скобочное выражение;

2) если P - правильное скобочное выражение, то (P) -

правильное скобочное выражение;

3) если P и Q - правильные скобочные выражения, то PQ -

правильное скобочное выражение.

Даны натуральное число п и последовательность символов

...,,, каждый из которых - круглая скобка. Определить, является

ли последовательность

...,, правильным скобочным выражением.

§ 35. Перебор и его сокращение

1028. Даны натуральные числа т,

aa ...,,

. В

последовательности

aa ...,,

выбрать подпоследовательность

iii

aaa ...,,,

( niii

≤<<<≤ ...0

) такую, что maa

=++...

Если такую подпоследовательность выбрать невозможно, то следует

сообщить об этом.

При решении этой задачи полезно следующее соображение.

Чтобы выбрать подпоследовательность из последовательности

aa ...,,

, нужно про каждый член

aa ...,,

, решить, принимается он в

подпоследовательность или нет. Может возникнуть следующая

ситуация: относительно членов

aa ...,,

( i < n ) приняты какие-то

решения, после этого обнаружилось, что, как бы мы ни распоряжались

остальными п - i членами, нам все равно не удастся получить

подпоследовательность, удовлетворяющую поставленному условию

(например, если сумма нескольких положительных чисел больше m, то

невозможно добавить к ним ещё несколько положительных чисел так,

чтобы сумма стала равна m). В этом случае можно сразу исключить из

рассмотрения все подпоследовательности, первые члены которых

выбраны из

aa ...,,

в соответствии с принятыми решениями.

1029. Получить все расстановки 8 ладей на шахматной доске,

при которых ни одна ладья не угрожает другой.

Здесь полезно соображение, аналогичное приведенному в

предыдущей задаче. Если расставлены ладьи в i первых вертикалях ( i

< 8 ) обнаружилось, что i-я ладья угрожает ладье в какой-то вертикали

с меньшим номером, то можно далее не заниматься теми

расстановками ладей, которые предполагают то же самое

расположение в первых вертикалях *).

*) Такого рода соображения оказываются полезными и при решении

всех дальнейших задач этого параграфа.

1030. Дано натуральное число т. Получить т расстановок 8

ферзей на шахматной доске, при которых ни один из ферзей не

угрожает другому. Если т больше, чем общее число таких

расстановок, то следует получить все расстановки.

1031. Получить все перестановки элементов 1, ..., 6.

1032. Получить все сочетания из 10 элементов 1, ..., 10, по 4

элемента в каждом.

1033. Получить все размещения из 9 элементов 1, . . ., 9, по 5

элементов в каждом.

1034. Получить все полные перестановки 10 элементов 1, ..., 10

(перестановка

pp ...,,

элементов 1, ..., п называется полной , если

≠ для i = 1, ..., п).

1035. Указать маршрут коня. Начинающийся на одном

заданном поле шахматной доски и оканчивающийся на другом.

Никакое поле не должно встречаться в маршруте дважды.

1036. Лабиринт может быть задан матрицей соединений, в

которой для каждой пары комнат указано, соединены ли они

коридором (см. задачу 626). Даны матрица соединений для лабиринта

из п комнат и номера комнат i, j ( njni ≤≤≤≤ 1,1 ). Построить путь из

комнаты с номером i в комнату с номером j.

1037. Дана матрица соединений некоторой линии (см. задачу

626), содержащей 6 узлов. Выяснить, существует ли замкнутый путь,

состоящий из некоторых звеньев линии, который проходит через

каждый из 6 узлов ровно один раз. Если такой путь существует, то

построить соответствующую ему последовательность номеров узлов.

(Для линии, изображенной на рис. 33, последовательность узлов будет,

например, 1, 2, 3, 4, 5, 6.)