Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию
Подождите немного. Документ загружается.

а) заменить на запятую;
б) удалить из последовательности.
*) Задачи 312 – 316 допускают строковые варианты.
313. Даны символы s
1
, …, s
n
. Если последовательность s
1
,…, s
n
является палиндромом , т.е. s
1
= s
n
, s
2
= s
n – 1
, …, то оставить ее без
изменения, иначе получить последовательность s
1
, s
2
,…, s
n – 1
, s
n
, s
n – 1
,
…, s
2
, s
1
.
314. Даны символы s
1
, …, s
66
. Если последовательность s
1
,… ,
s
66
такова, что s
1
= s
34
, s
2
= s
35
, …, s
33
= s
66
, то оставить ее без
изменения, иначе получить последовательность s
1
, s
2
, … , s
66
, s
1
, s
2
,…,
s
66
.
315. Даны символы s
1
, …, s
80
. Определить количество неверных
равенств среди:
а) s
1
= s
41
, s
2
= s
42
, ... , s
40
= s
80
;
б) s
1
= s
80
, s
2
= s
79
, ... , s
40
= s
41
.

316. Даны натуральное число n, символы s
1
,… , s
n
. Будем
рассматривать слова, образованные символами, входящими в
последовательность s
1
, …, s
n
(см. задачу 269), считая при этом, что
количество символов в каждом слове не превосходит 15.
а) Найти какое-нибудь слово, оканчивающееся буквой д (если
таких слов нет, то сообщить об этом).
б) Найти какое-нибудь слово, начинающееся буквой а и
оканчивающееся буквой я (если таких слов нет, то сообщить об этом).
в) Удалить из s
1
,…, s
n
все слова с нечетными порядковыми
номерами и перевернуть все слова с четными номерами. Например,
если n = 21 и данная последовательность символов представляет собой
последовательность
во_что_бы_то_ни_стало,
то должна получиться последовательность
отч_от_олатс.
г) Удалить из s
1
,… , s
n
все слова, в которых встречается не более
двух различных букв.
д) Удалить из s
1
, …, s
n
все слова, оканчивающиеся группой букв
кая или кое.

§10. Вложенные циклы
317. Даны действительные числа a
1
,…, a
10
. Вычислить
10
10
2
21
a aa +…++ .
318. Дано натуральное число n. Получить f
0
f
1
… f
n
, где
f
i
= +
+
+
+ 2
1
1
1
22
ii
…
1
1
2
++
+
ii
.
319. Даны действительные числа a
1
,… , a
24
. Получить
последовательность b
1
, …, b
10
, где b
1
= a
1
+a
2
+ … +a
24
, b
2
= a
1
2
+ a
2
2
+
… + a
24
2
,… , b
10
= a
1
10
+ a
2
10
+ … + a
24
10
.
320. Вычислить
åå
==
−
15
1
2
10
1
3
)(
lk
lkk
.
321. Даны натуральные числа m, n, действительные числа a
1
, a
2
,
..., a
mn
. Вычислить a
1
a
2
… a
m
+a
m+1
a
m+2
… a
2m
+a
(n – 1 ) m+1
a
(n – 1 ) m+2
… a
nm
.
322. Найти натуральное число от 1 до 10 000 с максимальной
суммой делителей.
323. Дано натуральное число n. Получить все натуральные
числа, меньшие n и взаимно простые с ним.
324. Даны целые числа p и q. Получить все делители числа q,
взаимно простые с p.
325. Дано натуральное число n. Получить все простые делители
этого числа.
326. Найти наименьшее натуральное число n, представимое
двумя различными способами в виде суммы кубов двух натуральных
чисел x
3
+y
3
(x ≥ y).
327. Даны натуральные числа a, b (a ≤b). Получить все простые
числа p, удовлетворяющие неравенствам a ≤p ≤b.
328. Найти 100 первых простых чисел.
329. Даны натуральные числа n, m. Получить все меньшие n
натуральные числа, квадрат суммы цифр которых равен m.
330. Натуральное число называется совершенным, если оно
равно сумме всех своих делителей, за исключением себя самого. Число
6 – совершенное, так как 6 = 1+2+3. Число 8 – не совершенное, так как
8 ≠ 1+2+4.Дано натуральное число n. Получить все совершенные числа,
меньшие n.
331. Дано натуральное число n. Можно ли представить его в
виде суммы трех квадратов натуральных чисел? Если можно, то
а) указать тройку
z
y,
x
, таких натуральных чисел, что
222
zyxn ++= ,
б) у казать все тройки
z
y,
x
,
таких натуральных чисел, что
222
zyxn ++= .
332. Известно, что любое натуральное число можно представить
в виде суммы не более чем четырех квадратов натуральных чисел или,
что то же самое, в виде суммы четырех квадратов неотрицательных

целых чисел (теорема Лагранжа). Дано натуральное n; указать такие
неотрицательные
t
z
,y,x,
, что
2222
tzyxn +++= .
333. Даны натуральные числа
()
.m,n...,nm,
m
2
1
≥ Вычислить
)НОД(
m
n...,n, , воспользовавшись для этого соотношением
()
kkk
nn...,n,n...,n, )НОД(НОД)НОД(
1−
= (k = 3, …, n)и алгоритмом
Евклида (см. задачу 89).
334. Вычислить
а)
åå
==
+
100
1
50
1
2
1
ij
ji
; б)
()
åå
==
+
100
1
60
1
43
sin
ij
ji ;
в) ;
ji
ij
ij
åå
==
+
+−
100
1
100
1
1
г)
åå
==
+
100
11
2
1
i
i
j
ij
335. Дано натуральное число n. Вычислить:
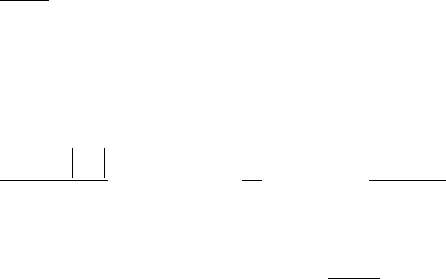
а)
()
;1
1
2
å
=
+
n
k
k...kk
б)
å
=
n
k
k
k
1
;
в)
()
;
!
1
1
2
å
=
n
k
k
г)
()
()
å
=
+−
n
k
k
k
1
2
!121
336. Даны натуральное число n, действительное число x.
Вычислить:
а)
()
()
å
=
+
n
i
i
xi
1
2
!
!2
; б)
()
()
å
=
+
−
n
k
k
k
k
x
n
1
!1!
1
!
1
;
в)
å
=
n
k
kk
xk
1
2
; г)
åå
==
+
n
k
n
km
m
kx
1
.
337. Даны действительные числа ba, … b)(a < , натуральное
число n , функция (x)fy = определенная на отрезке
[]
ba, . Вывести
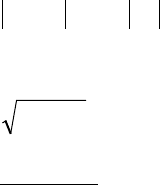
на печатающее устройство график функции. Для построения графика
вычислить значения функции )(xfy
ii
= , где
a)/n(bhniih,ax
i
−==+= ,,....1,,0,
Ось Ox расположить вертикально, ось Oy - горизонтально. Шаг по оси
Ox – это переход на новую строку, шаг по оси Oy –позиция
следующего символа в текущей строке. Точки графика изображать
символом *.
Рассмотреть следующие функции:
а) 400cossin ===+= nπ,b,a,xxy ;
б)
50cos3sin2 ==−=+= nπ,bπ,ax,xy ;
в)
03211
4
==−=+= n,b,a,xy ;
г)
4031
1
1
2
==−=
+−
= n,b,a,
,xx
y ;
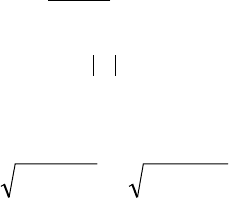
д) 5041
2
3
2
==−=
+
−
= n,b,a,
x
x
y ;
е)
4031
2
==−==
−
n,b,a,exe
x
;
ж)
50222sin ==−==
−
π, , nb,π/ax,ey
x
;
з)
503322
3
2
3
2
==−=−−+ n, b, a,)(x)(x .
338.Даны натуральное число n , целые числа
251
. , a..,a ,
n
,b...,b
1
.
Среди
251
. , a..,a нет повторяющихся чисел, нет их и среди
n
,b...,b
1
.
а) Построить пересечение последовательностей
251
,a...,a и
n
,b...,b
1
(т.е. получить в каком-нибудь порядке все числа,
принадлежащие последовательности
251
. , a..,a
и последовательности
n
,b...,b
1
одновременно)+.
б) Построить объединение данных последовательностей.
