Ablowitz M.A. Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons

Подождите немного. Документ загружается.

3.4 Linear KdV equation 55

The Fourier solution to (3.19) is given by

u(x, t) =

2π



ˆu

(k)e

i(kx−ω(k)t)

dk.

Substituting this into (3.19), the dispersion relation is found to be ω(k) = −k

which implies

u(x, t) =

2π



(

(k)e

i(kx+k

dk.

By the convolution theorem, see Ablowitz and Fokas (2003) this can also be

written in the form

u(x, t) =

(3t)

1/3





x − x



(3t)

1/3





) dx



where Ai denotes the the Airy function; see (3.22)–(3.23).

3.4.1 Stationary phase, x/t < 0

The method of stationary phase uses the Fourier integral in the form

u(x, t) =

2π



ˆu

(k)e

iφ(k)t

dk,

where φ = kχ + k

and χ = x/t. The important quantities are φ



= χ + 3k

= 0,

0±

= ±

−x

, and φ



= 6k. Stationary phase is applied only for real stationary

points. In this case, when x/t < 0, k

0±

= ±

√

x/(3t)

are real.

Since we have two stationary points, we add the contributions from both of

them to form our asymptotic estimate. Recalling that the general form of the

stationary phase result is

u(x, t) ∼



ˆu

0 j

)



2πt|φ



0 j

iφ(k

0 j

)t+iμ

π/4

where the sum is over all stationary points, we have, in our particular case,

φ(k

0±

) = ∓2

3/2



0±

) = ±2

√

= sgn(φ



0±

)) = ±1,

u(x, t) ∼

ˆu





√

πt

1/4

cos



3/2

t −

−

(





, (3.20)

56 Asymptotic analysis of wave equations

where we deﬁne ˆu

(k) ≡|ˆu

(k)|e

(

(k)

and use the relation ˆu

(k) = ˆu

∗

(−k).

Equation (3.20) is the leading asymptotic estimate for t  1, when x/t < 0.

3.4.2 Steepest descent, x/t > 0

In this section we introduce the asymptotic method of steepest descent by

working through an example with the linear KdV equation (3.19). The steep-

est descent technique is similar to that of stationary phase except we deﬁne our

Fourier integral with complex-valued φ as follows

I(t) =



f (z)e

tφ(z)

dz,

where C is, in general, a speciﬁed contour, which for Fourier integrals is

(−∞, ∞). In contrast, the stationary phase method uses the exponential in the

form e

iφ(k)t

where φ(k) ∈ R and the contour C is the interval (−∞, ∞). We are

interested in the long-time asymptotic behavior, t  1. We can ﬁnd the dom-

inant contribution to I(t) whenever we can deform (by Cauchy’s theorem if

deformations are allowed) on to a new contour C



called the steepest descent

contour, deﬁned to be the contour where φ(z) has a constant imaginary part:

Im φ(χ) = constant. The theory of complex variables then shows that Re{φ}

has its most rapid change along the steepest descent path (Ablowitz and Fokas,

2003; Erdelyi, 1956; Copson, 1965; Bleistein and Handelsman, 1986). Hence,

this asymptotic scheme will incorporate contributions from points along the

steepest descent contour with the most rapid change, namely at saddle points,



) = 0 corresponding to a local maxima. The method takes the following

general steps:

(a) Find the saddle points φ



) = 0; they can be complex.

(b) Use Cauchy’s theorem to deform the contour C to C



, the steepest descent

contour through a saddle point z

. The steepest descent contour is deﬁned

by Im{φ(z)} = Im{φ(z

)}. Use Taylor series to expand about the sad-

dle point and keep only the low-order terms when ﬁnding the dominant

contribution.

Let us now study the asymptotic solution for the KdV equation (3.19) with

x/t > 0. The Fourier solution takes the form

u(x, t) =

2π



ˆu

(k)e

tφ(k)

where φ(k) = i(kx/ t + k

) and C is the real axis: −∞< k < ∞. In this regime,

x/t > 0, φ



(k)  0 for all k ∈ C, and we can perform integration by parts,

as in (3.3), to prove that u(x, t) ∼ o(t

−n

) for all n. But this does not give us

the exact rate of decay, though we expect it is exponential. Steepest descent

3.4 Linear KdV equation 57

gives the exponential rate of decay under suitable assumptions. First we ﬁnd

the saddle points: φ



(k) = i(x/t + 3k

) = 0 implies that we have two saddle

points, k

= ±i

Next, we determine the steepest descent contour: we wish to ﬁnd the curves

deﬁned by the relations Im{φ(k) − φ(k

)} = 0 and choose one that “makes

sense”, namely that the integral will converge along our choice of contour. In

practice, one can expand φ(k) in a Taylor series near a saddle point, keep the

second-order terms, and use them to determine the steepest descent contour. In

our case, this gives

Im{φ(k) −φ(k

)} = Im



)

(k − k

)

= Im

∓3





1/2

2iθ

= 0

where we have deﬁned k − k

= r

iθ

Let us ﬁrst look at the case k

:WewishtomakeIm

−3





1/2

2iθ

= 0

for all x/t > 0. This requires that Im{e

2iθ

} = 0orsin(2θ) = 0. This is true when

θ = 0, π/2, π,3π/2, 2π,... In order to choose a speciﬁc contour, we must

get a convergent result when integrating along this contour. In particular, we

need Re



−3(x/3t)

1/2

2iθ



< 0or−cos(2θ) < 0 so that we have a decaying

exponential. Therefore, we choose θ = 0,π.

Now, for the k

−

case, the choices for θ are the same as before, namely

Im{φ(k) − φ(k

−

)} = 0 when θ = 0, π/2, π,3π/2, 2π,... But this time, the

convergent integral relation for the real part requires that cos(2θ) < 0, so θ

must be π/2or3π/2. We can rule out these choices by considering the contour

that passes through the point k

−

= −i

. Starting at −∞, it is impossible to

pass through the point k

−

with local angle π/2or3π/2 and continue on to +∞.

There is a “turn” at k

−

that sends the contour down to −i∞ and we cannot reach

+∞ as required.

Our contour locally (near k

) follows the curve C



iθ

∈ C

iθ

k − i

, k ∈ (−∞, ∞)

. Of the two possible choices for θ,wetakeθ = 0so

that we have a positively oriented contour. In order to satisfy Cauchy’s theo-

rem, we must smoothly transition from −∞ up to the curve deﬁned near k

and

then back down to +∞. This is not a problem for us as we are only interested

in what happens on the contour near k

Now that we have found our steepest descent contour, we evaluate the

Fourier integral along this contour using Cauchy’s theorem. Assuming no poles

between the contours C and C



, we deform the contour C to C



and ﬁnd the

58 Asymptotic analysis of wave equations

asymptotic estimate, with the dominant contribution from the saddle point k

to be

u(x, t) ∼

2π





ˆu

tφ(k

)



)(z−k

)

dz,

2π

ˆu





−2





3/2



∞

−∞

−3

dr,

ˆu





2π

√





1/4

−2





3/2



∞

−∞

−s

ds,

ˆu





√

πt





1/4

−2





3/2

. (3.21)

In going from the ﬁrst line to the second line, we made the change of variable

z −k

= r. From the second line to the third, the substitution r = s/





1/2

was made. The last line results from the evaluation of the Gaussian integral



−s

ds =

√

π.Wealsoassumedthatˆu

(k) is analytically extendable in the

upper half-plane. If ˆu

(k) had poles between C and C



, then these contribu-

tions would need to be included; indeed they would be larger than the steepest

descent contribution.

3.4.3 Similarity solution, x/t → 0

Motivated by the formulas (3.20) and (3.21), let us look for a similarity solution

of the linear KdV equation (3.19) with the form

sim

(x, t) =

(3t)



(3t)



Substituting this ansatz into (3.19) and calling η = x/(3t)

, we obtain the

equation



(3t)

p+3q

−

(3t)

p+1

(3pf + 3qη f



) = 0.

To obtain an ODE independent of t requires q = 1/3; for a linear problem; p is

free and is ﬁxed depending on additional (e.g., initial) conditions. The above

asymptotic analysis to the IVP implies (based on asymptotic matching of the

solution – see below) that p = 1/3 as well. Integrating the above equation once

gives



− η f = c

= 0, (3.22)

3.4 Linear KdV equation 59

where we take f → 0asη →∞. This equation is known as Airy’s equation.

The bounded solution to this ODE is a well-known special function of mathe-

matical physics and is denoted by Ai(η) (up to a multiplicative constant), which

has the integral representation (Ablowitz and Fokas, 2003)

Ai(η) =

2π



∞

−∞

i(sη+s

/3)

ds. (3.23)

As with the linear Schr

odinger equation (3.12), we can now write the self-

similar asymptotic solution to the linear KdV equation as

u(x, t) ∼ ˆu

(0)u

sim

(x, t) =

ˆu

(0)

(3t)

1/3



(3t)

1/3



An alternative, and in this case improved, way of doing this is starting with the

Fourier integral solution of this equation (as we have done before)

u(x, t) =

2π



(

(k)e

i(kx+k

and changing the integration variable to s deﬁned by k = s/(3t)

1/3

. This gives

u(x, t) =

2π(3t)

1/3



(



(3t)

1/3



exp



(3t)

1/3

2

ds.

Note that when x/(3t)

1/3

= O(1) (recall x/t is small) the exponent is not rapidly

varying. We assume ˆu(k) is smooth. Therefore, as t →∞we can expand u

inside the integral in a Taylor series, which gives

u(x, t) =

(

(0)

2π(3t)

1/3



i(sη+s

/3)

ds +

(



(0)

2π(3t)

2/3



i(sη+s

/3)

ds + ···,

where η = x/(3t)

1/3

.Using



(η) =

2π



∞

−∞

ise

i(sη+s

/3)

ds,

we arrive at the asymptotic expansion for x/(3t)

1/3

= O(1),

u(x, t) ∼

(

(0) Ai(η)

(3t)

1/3

−

(



(0)Ai



(η)

(3t)

2/3

+ ···. (3.24)

3.4.4 Matched asymptotic expansion

We have succeeded in determining the asymptotic behavior of the solution to

the linear KdV equation (3.19) in three diﬀerent regions: x/t < 0, x/t →

0, and x/t > 0. Each region required a diﬀerent asymptotic technique. Now

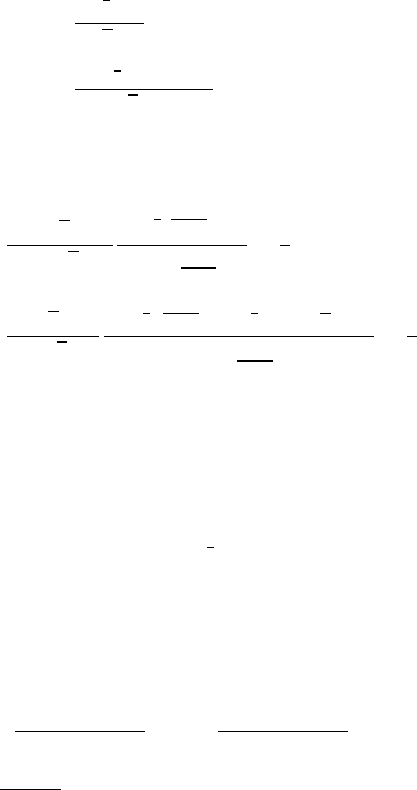
60 Asymptotic analysis of wave equations

we will see how the Airy function matches the seemingly disparate solutions

together.

Either applying the method of steepest descent directly on the integral solu-

tion (3.23) of the Airy equation (Ablowitz and Fokas, 2003) or consulting a

reference such as the Handbook of Mathematical Functions (Abramowitz and

Stegun, 1972) reveals that

Ai(η) ∼

−

3/2

√

πη

1/4

as η → +∞,

Ai(η) ∼

cos



3/2

− π/4



√

π|η|

1/4

as η →−∞.

Then we rewrite (3.20) and (3.21) in the following form:

u(x, t) ∼

ˆu







1/2



√

−



(3t)

1/3



3/2

(3t)

1/3



(3t)

1/3



1/4

> 0

u(x, t) ∼

ˆu



1/2



√

cos



(3t)

1/3

3/2

−

(



1/2



(3t)

1/3

(3t)

1/3

1/4

< 0.

Comparing the previous two sets of equations, we will see that this can be

interpreted as a slowly varying similarity solution involving the Airy function

that matches the asymptotic behavior in all three regions. Calling η = x/(3t)

1/3

weseethattheregimex/t < 0, η →−∞, exhibits oscillatory behavior and

decays like |η|

−1/4

just like the Airy function. When x/t > 0, η →∞,wehave

exponential decay that behaves like e

−

3/2

/η

1/4

. We further notice that the

formulas (3.20) and (3.21) are valid for x/t = O(1) and |η|1. As x/t → 0,

they match to the solution (3.24), which is valid for η = O(1). We also note

that further analysis shows that there is a uniform asymptotic expansion that is

valid for all three regions of



x/(3t)

1/3



u(x, t) ∼

ˆu

) + ˆu

(−k

)

2(3t)

1/3

Ai(η) −

ˆu

) −

(

(−k

)

2ik

(3t)

2/3



(η) + ...,

where k

√

−x/(3t) (see Figure 3.1). There is, in fact, a systematic method

of ﬁnding uniform asymptotic expansions (Chester et al., 1957).

3.5 Discrete equations 61

(3t)

1/3

= O(1)

(3t)

1/3

−x

(3t)

1/3

Figure 3.1 Asymptotic expansion for the linear KdV equation (3.19).

3.5 Discrete equations

It is well known that discrete equations arise in the study of numerical

methods for diﬀerential equations. However, discrete equations also arise in

important physical applications, cf. Ablowitz and Musslimani (2003) and

Christodoulides and Joseph (1998). For example, consider the semidiscrete

linear free Schr

odinger equation for the function u

(t) = u(nh, t)

∂u

∂t

n+1

− 2u

+ u

n−1

= 0, (3.25)

with h > 0 constant and given initial values u

(t = 0) = f

, with f

→ 0suﬃ-

ciently rapidly as |n|→∞. This equation can be used to solve the continuous

free Schr

odinger equation numerically, in which case the parameter h is taken

to be suﬃciently small. However, as described in the references, this semidis-

crete equation also arises in the study of waveguide arrays in optics, in which

case h can be O(1). In either case, we can study this equation using integral

asymptotics (Ablowitz and Segur, 1979, 1981).

3.5.1 Continuous limit

Before deriving the exact solutions of (3.25) and their long-time asymptotics,

it is important to understand the “continuous limit” of this equation as h → 0.

To do that we imagine that x = nh is a continuous variable with n large and

h =Δx small; that is, n →∞, h → 0, and nh → x. We can then formally

expand the solution in a Taylor series around x in the following way:

62 Asymptotic analysis of wave equations

n±1

(t) = u(nh ± h, t) = u(x ± h, t),

≈ u(x, t) ± hu

(x, t) +

(x, t) + ···.

Substituting this expansion into (3.25) and keeping O(1) terms leads to the

continuous free Schr

odinger equation,

+ u

= O(h

The initial conditions can be approximated in a similar manner, i.e., if u

(t =

0) = f

then in the continuous limit u(x, 0) = f (x).

3.5.2 Discrete dispersion relation

In analogy to the continuous case, we can ﬁnd wave solutions to (3.25) that

serve as the basic building blocks for the solution. Similar to the constant coef-

ﬁcient continuous case, we can look for wave solutions (or special solutions)

in the form

(t) = Z

−iωt

where Z = e

ikh

. Note that in the continuous limit i.e., as nh → x,wehave

= e

iknh

→ e

ikx

, so this solution becomes e

i(kx−ωt)

, i.e., the continuous

wave solution. Substituting u

into (3.25) leads to the discrete dispersion

relation

ω +

Z − 2 + 1/Z

= 0.

It is convenient to use Euler’s formula (Z + 1/Z)/2 = cos(kh) to rewrite the

dispersion relation as

ω(k) =

2[1 − cos(kh)]

. (3.26)

This is the dispersion relation for (3.25). Taking the continuous limit h → 0,

k = O(1) ﬁxed, and using a Taylor expansion leads to

ω(k) = k

which is exactly the dispersion relation for the continuous Schr

odinger equa-

tion. But it is important to note that the dispersion relations for the discrete and

continuous problems are markedly diﬀerent for large values of k.

3.5 Discrete equations 63

3.5.3 Z transforms and discrete Fourier transforms

The next step in the analysis is to represent the general solution as an integral

of the special (wave) solutions, in analogy to the Fourier transform. This kind

of representation is sometimes referred to as the Z transform. To understand it

better, let us recall some properties of the Fourier transform. In the continuous

case, recall we have the pair

u(x) =

2π



∞

−∞

(

u(k)e

ikx

dk,

(

u(k) =



∞

−∞

u(x)e

−ikx

dx.

Substituting the second into the ﬁrst and interchanging the integrals yields

u(x) =

2π



∞

−∞





∞

−∞

u(x



−ikx





ikx

dk,

2π



∞

−∞

u(x



)





∞

−∞

ik(x−x



)







∞

−∞

u(x



)δ(x − x



) dx



= u(x), (3.27)

where we have used that the delta function satisﬁes

δ(x) =

2π



∞

−∞

ikx

dk;

see Ablowitz and Fokas (2003) for more details.

Now, the Z transform (ZT) and its inverse (IZT) are given by

2πi

˜u(z)z

n−1

dz, (3.28)

˜u(z) =

∞



m=−∞

−m

, (3.29)

where the contour C is the unit circle in the complex domain. In analogy

with the Fourier transform (FT) pair, we substitute (3.29)into(3.28) and use

complex analysis to get that

64 Asymptotic analysis of wave equations

2πi



∞



m=−∞

−m



n−1

∞



m=−∞

2πi

n−m−1

∞



m=−∞

n,m

= u

, (3.30)

where the Kronecker delta δ

n,m

is 1 when n = m and zero otherwise. Here

we have relied on the fact that

2πi

dz, α integer, is equal to 1 only for a

simple pole, i.e., α = −1, and is otherwise equal to zero. Equation (3.30)using

complex analysis is the analog to (3.27)fortheZT.

In discrete problems it is convenient to put the ZT in a “Fourier dress”. We

can do that by substituting z with k according to z = e

ikh

. Since the contour

of integration is the (counterclockwise) unit circle, k ranges from −π/h to π/h

and z goes from −1 to 1. Thus, the ZT is transformed into the discrete Fourier

transform (DFT)

2πi



π/h

−π/h

˜u(z)e

ik(nh−h)

ihe

ikh

dk =

2π



π/h

−π/h

˜u(z)e

iknh

dk, (3.31)

using z(k) = e

ikh

. In the continuous limit as h → 0, we have h ˜u(z) = h˜u(e

ikh

) →

(

u(k), nh → x, u

= u(nh) → u(x) and we get the continuous FT

u(x) =

2π



∞

−∞

(

u(k)e

ikx

dk.

For the IZT there is a corresponding inverse DFT (IDFT), which can also be

obtained using z(k) = e

ikh

h˜u(z) = h

∞



m=−∞

−m

∞



m=−∞

u(mh)e

−i(mh)k

or, with mh → x, and noting that the Riemann sum tends to an integral with

h =Δx:

(

u(k) =



∞

−∞

u(x)e

−ixk

dx.

Thus, in the continuous limit one obtains the continuous IFT.