Абакумов А.И. Модели Неймана-Гейла
Подождите немного. Документ загружается.

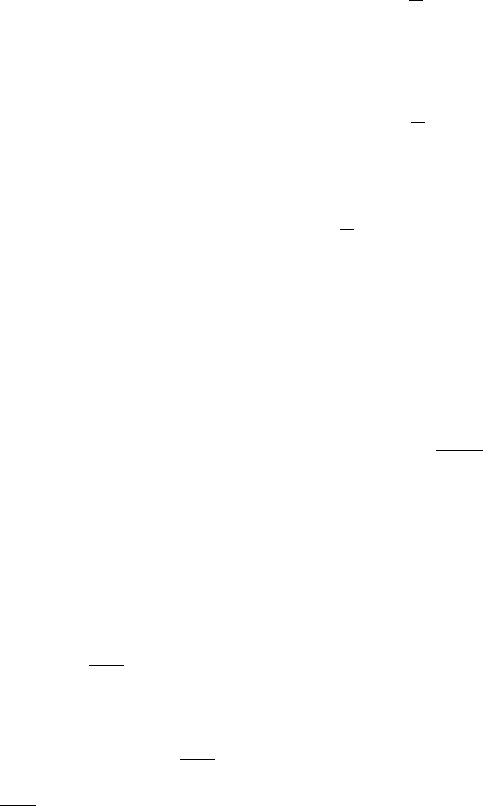
Теперь перейдём к доказательству теоремы о магистрали в сильной
форме.
Доказательство теоремы о магистрали в сильной форме.
Рассмотрим собственное множество A. Выполняются соотношения
G
k
(A) = f
−k
(∂
+
A) ∩ A, k ∈ N,
f
−k
(∂
+
A) ∩ A → G(A).
Выберем малое δ
1
> 0. Тогда из предыдущего следует, что существует
k
0
∈ N, что выполнено включение
f
−k
0
(∂
+
A) ∩ A ⊂ G(A) +
1
4
δ
1
S.
По лемме о множествах B
k
t
для достаточно больших t выполняется
B
k
0
t
⊂
f
−k
0
(∂
+
A) ∩ A
+
1
4
δ
1
S,
тогда
B
k
0
t
⊂ G(A) +
1
2
δ
1
S. (13)
Построим Q(δ
1
, t), Q(δ
1
) по функционалу ϕ ∈ (R
n
+
)
∗
, указанному в п. б)
теоремы.
Докажем, что ∀ t ≥ 0 выполняется включение
Q(δ
1
, t) + δ
1
S
∩ B
t
⊂ Q
δ
1
1 +
kϕk
c
t
, t
!
, (14)
где c
t
= max
y∈B
t
ϕ(y).
Действительно, пусть x ∈ (Q(δ
1
, t)+δ
1
S)∩B
t
. Тогда найдутся такие x
1
, x
2
,
что x = x
1
+ x
2
, ϕ(x
1
) ≥ (1 − δ
1
)c
t
, ϕ(x
2
) ≥ −δ
1
||ϕ||. Отсюда следует
ϕ(x) ≥
1 − δ
1
1 +
||ϕ||
c
t
c
t
, что означает справедливость соотношения
(14).
Обозначим через M = 2 +
||ϕ||
c
. Так как по лемме о множествах Q(δ, t)
c
t
→ c, то 1 +
||ϕ||
c
t
≤ M для достаточно больших t.
Тогда для этих t из (14) получаем
(Q(δ
1
, t) + δ
1
S) ∩ B
t
⊂ Q(Mδ
1
, t). (15)
41
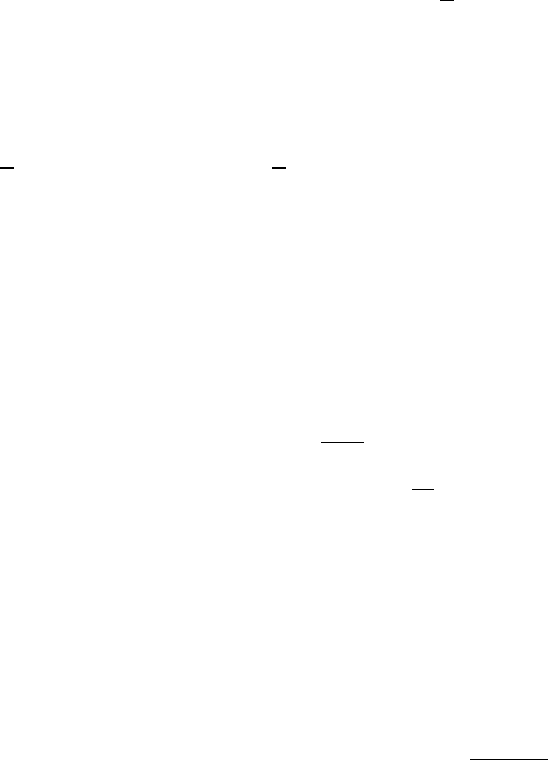
Из условия б) теоремы следует
G(A) ⊂ Q(δ
1
). (16)
Это включение обосновывается соотношениями G(A) ⊂ ∂
+
A, ∂
+
A ⊂
Q(δ
1
). Последнее верно из-за того, что ϕ постоянно на G(A), а это значе-
ние ϕ(G(A)) должно быть равно max
y∈A
ϕ(y) на основе свойств ∂
+
A.
Из леммы о множествах Q(δ, t) следует, что для достаточно больших t
Q(δ
1
) ⊂ Q(δ
1
, t) +
1
2
δ
1
S.
Отсюда и из формул (15), (16) получаем для достаточно больших t сле-
дующие включения:
G(A)+
1
2
δ
1
S
∩B
t
⊂
Q(δ
1
)+
1
2
δ
1
S
∩B
t
⊂
Q(δ
1
, t)+δ
1
S
∩B
t
⊂ Q(Mδ
1
, t).
Так как B
k
0
t
∩ B
t
= B
k
0
t
, то из последних включений и (13) следует суще-
ствование таких t
0
, k
0
, что
B
k
0
t
⊂ Q(Mδ
1
, t) для t ≥ t
0
. (17)
Возьмём произвольное ε > 0. По лемме Мак-Кензи существует такое δ >
0, что ∀ (x, y) ∈ Z с условием ρ
(x,y)
kxk
, N
α
≥ ε выполняется неравенство
ϕ(y) < (1 − δ)ϕ(x). Положим в (17) δ
1
=
1
M
δ
2
. Тогда ∀ t > t
0
выполняется
B
k
0
t
⊂ Q(δ
2
, t). Последовательность (c
t
)
∞
t=0
, где c
t
= max
y∈B
t
ϕ(y), сходится к
c = max
y∈A
ϕ(y). В этом случае t
0
можно считать таким большим, что ∀ t > t
0
max
y∈B
t
ϕ(y) ≤ (1 + δ) max
y∈B
t+1
ϕ(y).
Рассмотрим конечную траекторию (x
t
)
T
t=0
с T > t
0
+ k
0
. Пусть для неко-
торого t, t
0
< t < T − k
0
выполняется ρ
(x
t−1
,x
t
)
kx
t−1
k
, N
α
≥ ε. Тогда по
лемме Мак-Кензи выполняются неравенства ϕ(x
t
) < (1 − δ)ϕ(x
t−1
) ≤
(1 − δ) max
y∈B
t−1
ϕ(y) ≤ (1 − δ
2
) max
y∈B
t
ϕ(y). Получаем x
t
/∈ Q(δ
2
, t), то есть
x
t
/∈ B
k
0
t
.
По определению
B
k
0
t
= G
k
0
(B
t
) = f
−k
0
(∂
+
B
t+k
0
) ∩ B
t
.
42

Так как x
t
∈ B
t
и x
t
/∈ B
k
0
t
, то x
t
/∈ f
−k
0
(∂
+
B
t+k
0
). Отсюда следует, что
f
k
0
(x
t
) ∩ ∂
+
B
t+k
0
= ∅. Это означает, что x
t+k
0
/∈ ∂
+
f
t+k
0
(x
0
), а отсюда сле-
дует, что последовательность (x
τ
)
t+k
0
τ=0
не оптимальна и последовательность
(x
t
)
T
t=0
также не оптимальна. Следовательно, для любой оптимальной ко-
нечной траектории (x
t
)
T
t=0
(T > t
0
+ k
0
) выполняется неравенство
ρ
(x
t−1
, x
t
)
kx
t−1
k
, N
α
!
< ε
для t
0
< t < T − k
0
.
Теорема о магистрали в сильной форме полностью доказана.♦
2.4 Упражнения
Решить следующие задачи, примеры или доказать сформулированные
факты. Соотвествующие обозначения и понятия приведены в тексте раз-
дела.
1. Сформулировать определение полунепрерывности сверху для функ-
ционалов на языке последовательностей.
2. Множество D в доказательстве утверждения 4.5 является выпуклым
замкнутым конусом.
3. Для неймановского показателя роста существует набор
(α(z), (¯x, ¯y), ¯ϕ), для которого выполнены все условия равновесия,
кроме, возможно, ¯ϕ(¯y) > 0.
4. Множество N
α
является гранью конуса Z.
4. kxk
A
удовлетворяет всем условиям нормы.
5. Формула (7) определяет функцию расстояния.
Заключение
Многозначные отображения позволяют создать общее описание про-
цессов экономической динамики. Сюда вкладываются модели Леонтьева
43
"затраты - выпуск"и серия моделей Неймана и Неймана-Гейла. В наиболее
общем виде проявляются свойства магистральности оптимальных траек-
торий. Приведены две формы теоремы о магистралях - слабая и сильная.
В различных постановках моделей экономической динамики теоремы о
магистральных свойствах оптимальных траекторий могут иметь различ-
ную форму, но принципиально эти формы мало отличаются от указанных
здесь вариантов.
Список литературы
1. Канторович Л.В. Математические методы организации и планирова-
ния производства. Л.: Изд-во ЛГУ, 1939.
2. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функцио-
нального анализа. М.: Наука, 1968.
3. Кроновер Р.М. Фракталы и хаос в динамических системах. Основы
теории. М.: Постмаркет, 2000.
4. Ланкастер К. Математическая экономика. М.: Советское радио, 1972.
5. Левин М.И., Макаров В.Л., Рубинов А.М. Математические модели
экономического взаимодействия. М.: Наука, 1993.
6. Макаров В.Л., Рубинов А.М. Математическая теория экономической
динамики и равновесия. М.: Наука, 1973.
7. Никайдо Х. Выпуклые структуры и математическая экономика. М.:
Мир, 1972.
8. Треногин В.А. Функциональный анализ. М.: Наука, 1980.
9. Newmann, J. von. Ub er ein ¨okonomisches Gleichungssystem und ei ne
Verallgemeinerung das Brounerschen Fixpunkt-satzes, Ergebnisse eines
Math. Kolloguiums, No 8, Vienna, 1937.
44
