Абакумов А.И. Модели Неймана-Гейла
Подождите немного. Документ загружается.

двойственности выполняется равенство
max
y∈f
1
(x)
ψ(y) = inf
ϕ∈(f
0
1
)
−1
(ψ)
ϕ(x). (6)
Отсюда следует
p
χ
(x) = inf
ψ(f
0
2
)
−1
(χ)
inf
ϕ∈(f
0
1
)
−1
(ψ)
ϕ(x) =
= inf
ϕ∈(f
0
1
)
−1
◦(f
0
2
)
−1
(χ)
ϕ(x) = inf
ϕ∈(f
0
2
◦f
0
1
)
−1
(χ)
ϕ(x).
Множество (f
0
2
◦ f
0
1
)
−1
(χ) является K-опорным. Из определения следует,
что оно K
∗
-устойчиво (f
0
2
◦ f
0
1
)
−1
(χ) + K
∗
⊂ (f
0
2
◦ f
0
1
)
−1
(χ) и выпукло. Его
замкнутость вытекает из замкнутости отображений f
0
1
и f
0
2
. Из формулы
(6) получаем:
inf
ϕ∈(f
0
2
◦f
0
1
)
−1
(χ)
ϕ(x) > −∞.
Следовательно, (f
0
2
◦ f
0
1
)
−1
(χ) - K-опорное. Из связи опорных функциона-
лов и опорных множеств следует U
p
χ
= (f
0
2
◦f
0
1
)
−1
(χ). С другой стороны, из
определения двойственного отображения следует: U
p
χ
= ((f
2
◦ f
1
)
0
)
−1
(χ).
Отсюда:
(f
0
2
◦ f
0
1
)
−1
(χ) = ((f
2
◦ f
1
)
0
)
−1
(χ),
то есть (f
0
2
◦ f
0
1
)
−1
= ((f
2
◦ f
1
)
0
)
−1
. Отсюда следует равенство f
0
2
◦ f
0
1
=
(f
2
◦ f
1
)
0
. Теорема доказана. ♦
Теорема о втором двойственном отображении. Пусть f ∈
F (K, Q). Тогда f
00
= nf.
Доказательство. Из теоремы двойственности и теоремы Фенхеля сле-
дует, что ∀ ψ ∈ Q
∗
(f
0
)
−1
(ψ) 6= ∅. Для x ∈ K определим функционал на
Q
∗
:
q
x
(ψ) = inf
ϕ∈(f
0
)
−1
(ψ)
ϕ(x).
По теореме двойственности
q
x
(ψ) = max
y∈f(x)
ψ(y). (7)
21
Из формулы (7) следует, что q
x
- сублинейный монотонный функционал
на Q
∗
. Обращаем внимание на разницу в формулах (5) и (7). В формуле
(5) в качестве аргумента выступают элементы конуса K, а в формуле (7)
- элементы конуса Q
∗
.
Пусть V
+
q
x
= V
q
x
∩Q. Напомним, что в данном случае V
+
q
x
=
n
y ∈ Q | ∀ ψ ∈
Q
∗
ψ(y) ≤ q
x
(ψ)
o
.
Предположим, что y ∈ f
00
(x). Тогда ∀ ψ ∈ Q
∗
∀ ϕ ∈ (f
0
)
−1
(ψ) выполняет-
ся ϕ(x) ≥ ψ(y). Отсюда следует, что q
x
(ψ) = inf
ϕ∈(f
0
)
−1
(ψ)
ϕ(x) ≥ ψ(y). Тогда
y ∈ V
+
q
x
. Отсюда следует, что f
00
(x) ⊂ V
+
q
x
.
Пусть, наоборот, y ∈ V
+
q
x
. Тогда ∀ ψ ∈ Q
∗
ψ(y) ≤ q
x
(ψ), y ∈ Q. От-
сюда следует, что ∀ ψ ∈ Q
∗
, ∀ ϕ ∈ K
∗
из условия ψ ∈ f
0
(ϕ) получается
ψ(y) ≤ ϕ(x). Это означает, что y ∈ f
00
(x) и V
+
q
x
⊂ f
00
(x).
Таким образом, доказано, что V
+
q
x
= f
00
(x).
Теперь докажем, что множество V
+
q
x
нормально. Пусть y ∈ V
+
q
x
, 0 ≤ z ≤
Q
y. Тогда z − 0 ∈ Q, т.е. z ∈ Q. Так как y ∈ V
+
q
x
, то ∀ ψ ∈ Q
∗
выполняется
неравенство ψ(y) ≤ q
x
(ψ). Отсюда следует, что 0 ≤ ψ(z) ≤ ψ(y) ≤ q
x
(ψ).
Это означает, что z ∈ V
+
q
x
. Отсюда следует, что множество V
+
q
x
нормально
относительно конуса Q. Равное ему множество f
00
(x) тоже является нор-
мальным.
Теперь докажем, что f
00
= nf. Множество nf(x) − Q является Q
∗
- суб-
опорным. При этом для ψ ∈ Q
∗
выполняется sup
y∈nf(x)−Q
ψ(y) = sup
y∈V
+
q
x
ψ(y).
Это следует из того факта, что sup
y∈nf(x)−Q
ψ(y) = max
y∈nf(x)
ψ(y) = max
y∈f(x)
ψ(y).
Последнее равенство следует из цепочки преобразований max
y∈nf(x)
ψ(y) ≤
max
y∈(f(x)−Q)∩Q
ψ(y) ≤ max
y∈(f(x)−Q)
ψ(y) = max
y∈f(x)
ψ(y) ≤ max
y∈nf(x)
ψ(y).
Отсюда по теореме об отображении h следует, что V
q
x
= nf(x) − Q и
V
+
q
x
= (nf(x) − Q) ∩ Q = nf(x).
Теорема доказана.♦
Следствие. 1. Для f ∈ F (K, Q) равенство f = f
00
выполняется тогда
22
и только тогда, когда f нормально. 2. Если f ∈ F (K, Q), то nf ∈ F (K, Q).
1.6 Упражнения
Решить следующие задачи, примеры или доказать сформулированные
факты. Соотвествующие обозначения и понятия приведены в тексте раз-
дела.
1. Привести примеры выступающих и воспроизводящих конусов в про-
странствах X = R
2
и X = R
3
.
2. Телесный конус является воспроизводящим.
3. Определить условия на конус K, при которых порядок ≤
K
станет
линейным.
4. Конечномерное нормированное пространство является полным.
5. Для выступающего конуса K конус K
∗
является воспроизводящим.
6. Если K - выпуклый конус, то ∀x, y ∈ K выполняется x + y ∈ K.
7. Если линейный функционал ϕ ∈ X
∗
равен нулю на некотором те-
лесном подмножестве пространства X, то ϕ ≡ 0 на всём пространстве
X.
8. Если K - выпуклый замкнутый конус, то K
∗
- также выпуклый за-
мкнутый конус.
9. Если K - выступающий конус, то K
∗
- воспроизводящий конус.
10. Если K - воспроизводящий конус, то K
∗
- выступающий конус.
11. Функционал p
U
является супераддитивным и положительно одно-
родным.
12. Множество Z
p
в доказательстве теоремы Фенхеля является выпук-
лым замкнутым конусом.
13. Если p ∈ Φ(K), то множество U
p
− K-опорное.
14. Если U ⊂ X
∗
, U − K-опорное, то функционал p
U
суперлинеен.
15. Если функционал q сублинеен, то −q суперлинеен.
23
16. Отображение g : P Φ(K) → Φ(K) является взаимно однозначным
отображением на все множество Φ(K).
17. Если q ∈ Ψ(K), то V
q
6= ∅ и ∀ x ∈ K q(x) = sup
ϕ∈V
q
ϕ(x).
18. Отображение h : QΨ(K) → Ψ(K) является взаимно однозначным
отображением на все множество Ψ(K).
19. Множество V
+
q
непусто тогда и только тогда, когда q принимает на
K неотрицательные значения.
20. В доказательстве теоремы о монотонных сублинейных функциона-
лах множество Z
q
является выпуклым замкнутым конусом.
21. В доказательстве теоремы о монотонных сублинейных функциона-
лах множество Z
0
является выпуклым замкнутым, но не конусом.
22. Квазилинейное отображение f : K → P (Q) является ограничен-
ным.
23. Функционал p
ψ
(5) положительно однородный.
24. Построить K
∗
для K = {(x
1
, x
2
) ∈ R
2
+
| x
1
= x
2
}.
25. Множество Z
0
является выпуклым замкнутым конусом.
26. Функционал q
x
(7) является сублинейным и монотонным.
27. В теореме о втором двойственном отображении множество nf(x)−Q
является Q
∗
- субопорным.
24
II Модели Неймана-Гейла
Через X по-прежнему обозначаем конечномерное нормированное про-
странство.
Модель Неймана-Гейла - это такой выпуклый замкнутый конус
Z ⊂ R
n
+
× R
n
+
, что ∀y 6= 0, (0, y) /∈ Z, P r
2
Z ∩ (
o
R
n
+
) 6= ∅. Модель Z назы-
вается правильной, если P r
1
Z = R
n
+
. В дальнейшем мы рассматриваем
правильные модели Неймана - Гейла.
Для пары (x, y) ∈ Z вектор x называется вектором затрат, а y - векто-
ром выпуска. Подчеркивая этот содержательный смысл векторов, иногда
пару (x, y) ∈ Z будем называть процессом.
По конусу Z можно построить многозначное отображение f : K → P (R
n
+
),
где K = P r
1
Z, f(x) = {y | (x, y) ∈ Z}. Отображение f называется про-
изводственным отображением модели Неймана-Гейла.
Утверждение о модели Неймана - Гейла. Конус Z - модель
Неймана-Гейла тогда и только тогда, когда соответствующее отображе-
ние f является квазилинейным многозначным отображением.
Доказательство.
Необходимость. Пусть конус Z - модель Неймана-Гейла. Определим мно-
жество K = P r
1
Z и отображение f: ∀x ∈ K f(x) = {y ∈ R
n
+
| (x, y) ∈
Z}.
Из выпуклости конуса Z получаем, что для: (x, y) ∈ Z, (u, v) ∈ Z спра-
ведливо (x + u, y + v) ∈ Z. Это означает супераддитивность f.
Положительная однородность f следует из определения конуса Z. Осталь-
ные свойства f прямо указаны в определении модели Неймана-Гейла.
Достаточность. Пусть f - квазилинейное многозначное отображение. Обо-
значим через Z график для f. Тогда Z является выпуклым замкнутым
конусом. Остальные свойства Z прямо указаны в определении квазили-
нейного отображения f.♦
25

Состоянием равновесия модели Неймана-Гейла называется набор
элементов σ = (α, (¯x, ¯y), ¯ϕ) с числом α > 0, парой (¯x, ¯y) ∈ Z и функцио-
налом ¯ϕ ∈ (R
n
+
)
∗
, для которых выполняются условия:
1) α¯x ≤ ¯y (неравенство понимается в смысле конуса R
n
+
);
2) ∀ (x, y) ∈ Z выполняется неравенство ¯ϕ(y) ≤ α ¯ϕ(x) и ¯ϕ(¯y) > 0.
Число α = α(σ) называется темпом роста модели Неймана-Гейла Z (или
производственного отображения f).
Утверждение о свойствах пар из модели Z. Для любых (x, y) ∈ Z
выполняются неравенства ¯ϕ(y) ≤ α ¯ϕ(x) и неравенство ¯ϕ(¯y) > 0 тогда и
только тогда, когда
1
α
¯ϕ ∈ f
0
( ¯ϕ).
Доказательство. Вспомним определение f
0
( ¯ϕ). А именно: f
0
( ¯ϕ) =
n
ψ ∈ (R
n
+
)
∗
| ∀x ∈ K ¯ϕ(x) ≥ max
y∈f(x)
ψ(y)
o
. Тогда верна следующая це-
почка эквивалентных преобразований: условие ∀(x, y) ∈ Z ¯ϕ(x) ≥
1
α
¯ϕ(y)
эквивалентно неравенству ¯ϕ(x) ≥ max
y∈f(x)
1
α
¯ϕ(y), а последнее эквивалентно
условию
1
α
¯ϕ ∈ f
0
( ¯ϕ). ♦
2.1 Темпы роста
Если Z модель Неймана - Гейла, то Z
0
также модель Неймана - Гейла
(с заменой R
n
на (R
n
)
∗
). Тогда и для Z
0
можно говорить о темпах роста.
Модель Z
0
будем называть двойственной по отношению к модели Z.
Утверждение о темпах роста двойственных отображений.
Пусть Z - модель Неймана-Гейла, f - производственное отображение в
этой модели, f ∈ F (K, R
n
+
). Тогда число α > 0 является темпом ро-
ста модели Неймана-Гейла в том и только в том случае, когда число
1
α
является темпом роста отображения f
0
.
Доказательство.
Необходимость. Пусть α - темп роста отображения f и (α, (¯x, ¯y), ¯ϕ) - со-
ответствующее равновесие. Тогда α¯x ≤ ¯y, откуда следует условие α¯x ∈
26
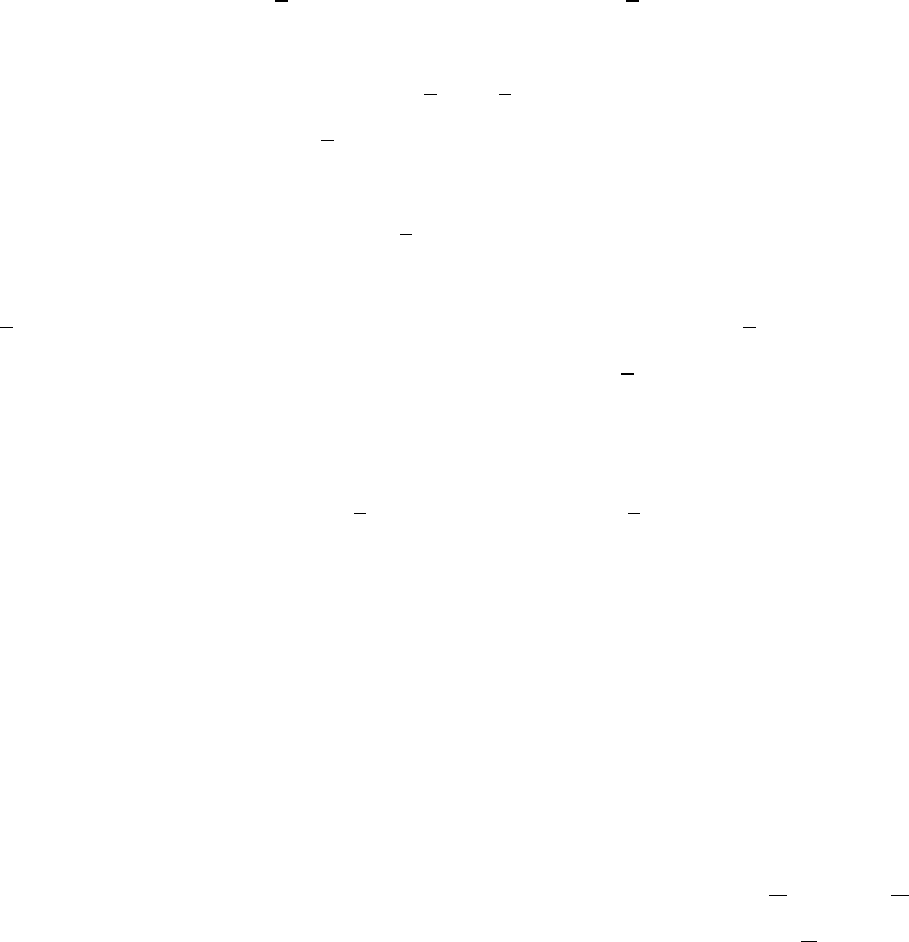
nf(¯x) = f
00
(¯x). Из условий равновесия следует, что ∀ (x, y) ∈ Z ¯ϕ(y) ≤
α ¯ϕ(x), то есть ¯ϕ(x) ≥
1
α
¯ϕ(y). Это влечёт за собой
1
α
¯ϕ ∈ f
0
( ¯ϕ) и ¯ϕ(¯x) > 0.
Из α¯x ∈ f
00
(¯x) следует ∀ ϕ ∈ K
∗
, ∀ψ ∈ f
0
(ϕ) выполняется неравенство
ϕ(¯x) ≥ ψ(α¯x). Это означает, что
1
α
,
¯ϕ,
1
α
¯ϕ
, ¯x
- равновесие для отобра-
жения f
0
. Следовательно,
1
α
- темп роста для отображения f
0
.
Достаточность. Пусть β - темп роста для отображения f
0
. Из доказан-
ной необходимости следует, что
1
β
- темп роста для отображения f
00
. От-
сюда следует существование равновесия для отображения f
00
= nf вида
(
1
β
, (¯x, ¯y), ¯ϕ). Это означает выполнение следующих условий:
1
β
¯x ≤ ¯y, ∀ x, y
при условии y ∈ f
00
(x) выполняется неравенство
1
β
¯ϕ(x) ≥ ¯ϕ(y), а также
выполняется неравенство ¯ϕ(¯y) > 0. Так как ¯y ∈ f
00
(¯x) = nf(¯x), то най-
дётся ¯z ∈ f(¯x) с условием ¯y ≤ ¯z. Так как ¯z ∈ f(¯x) ⊂ nf(¯x) = f
00
(¯x),
то выполняется неравенство
1
β
¯ϕ(¯x) ≥ ¯ϕ(¯z). Тогда (
1
β
, (¯x, ¯z), ¯ϕ) - состояние
равновесия для f.♦
Показателем роста процесса (x, y) ∈ Z называется число α(x, y) =
sup{α | αx ≤ y}.
Напомним, что в R
n
есть стандартный базис и любой x ∈ R
n
пред-
ставляется столбцом своих координат x =
x
1
.
.
.
x
n
!
. Введём обозначения
I = {1, . . . , n}, I
x
= {i ∈ I | x
i
> 0}. Тогда α(x, y) = min
i∈I
y
i
x
i
= min
i∈I
x
y
i
x
i
(условно будем считать, что при y
i
> 0 выполняется равенство
y
i
0
= +∞
и +∞ больше любого действительного числа).
Утверждение об отображении α. Отображение α : (x, y) 7−→
α(x, y) на Z\{0} является полунепрерывным сверху и положительно од-
нородным нулевой степени функционалом.
Доказательство. Положительная однородность нулевой степени оче-
видна. Докажем полунепрерывность сверху. Пусть (x
k
, y
k
) ∈ Z, (x
k
, y
k
) →
(x
0
, y
0
) (считаем x
0
6= 0 без ограничений общности). Пусть ˜α - предельная
27

точка последовательности α(x
k
, y
k
), ˜α = lim
i→∞
α(x
k
i
, y
k
i
). Из определений
следует, что α(x
k
i
, y
k
i
)x
k
i
≤ y
k
i
. Тогда ˜α < ∞ (иначе x
0
= 0), в пре-
деле ˜αx
0
≤ y
0
, откуда ˜α ≤ α(x
0
, y
0
). Это означает, что lim
n→∞
α(x
n
, y
n
) ≤
α(x
0
, y
0
).♦
Число α(Z) = max
(x,y)∈Z, ||(x,y)||=1
α(x, y) = sup
(x,y)∈Z, (x,y)6=0
α(x, y) назовем
неймановским показателем роста модели Z.
Замечание. Неймановский показатель роста α(Z) всегда положителен
и конечен.
Доказательство следует из того, что P r
2
Z∩
o
R
n
+
6= ∅, а неймановский
показатель роста достигается на некотором процессе, и пара (0, y) не при-
надлежит конусу Z ни при каком y 6= 0. ♦
Утверждение о неймановском показателе роста. Пусть Z - мо-
дель Неймана-Гейла. Тогда найдется такой функционал ¯ϕ ∈ (R
n
+
)
∗
, что
∀ (x, y) ∈ Z выполняется неравенство ¯ϕ(y) ≤ α(Z) ¯ϕ(x).
Доказательство. Обозначим D =
y −α(Z)x | (x, y) ∈ Z
. Это выпук-
лый замкнутый конус. Из определения α(Z) следует, что D ∩
o
R
n
+
= ∅. По
теореме отделимости для конуса следует существование такого линейного
функционала ¯ϕ, что ¯ϕ 6= 0 и max
z∈D
¯ϕ(z) = 0 ≤ min
u∈R
n
+
¯ϕ(u). Это означает, что
функционал ¯ϕ является искомым.♦
В работе [6] приводится пример, когда в модели Неймана-Гейла вообще
нет равновесных состояний. Все дело в том, что для неймановского по-
казателя роста α(Z) можно найти набор (α(Z), (¯x, ¯y), ¯ϕ) с выполнением
всех условий для состояния равновесия, кроме ¯ϕ(¯y) > 0. Поэтому даже
для неймановского показателя роста не всегда справедливо то, что он яв-
ляется темпом роста.
Пару (x, y) с α(x, y) = α(Z) назовем неймановским процессом.
Соответствующее неймановскому показателю роста состояние равновесия
28

(если оно существует) назовем неймановским состоянием равнове-
сия.
Неймановским темпом роста назовём неймановский показатель ро-
ста, являющийся темпом роста.
Утверждение о множестве C
α
. Пусть Z - модель Неймана-Гейла и
число α такое, что C
α
=
(x, y) ∈ Z | αx ≤ y
6= ∅, тогда найдется такая
пара (˜x, ˜y) ∈ C
α
, что ∀ (x, y) ∈ C
α
выполняются включения I
˜x
⊃ I
x
, I
˜y
⊃
I
y
.
Доказательство. В множестве C
α
существует конечное число пар
(x
i
, y
i
) (i = 1, m), для которых множества I
x
i
× I
y
i
попарно различны.
Тогда искомая пара есть
m
P
i=1
(x
i
, y
i
).♦
Согласно утверждению о множестве C
α
среди неймановских процессов
модели Z найдется такой процесс (ˆx, ˆy), что его множества I
ˆx
, I
ˆy
включают
в качестве подмножеств такие же множества любого другого неймановско-
го процесса. Тогда пару (ˆx, ˆy) будем называть полным неймановским
процессом. Множество I
ˆy
в этом случае обозначим через I(Z).
Рассмотрим следующую процедуру построения конусов. Пусть Z - мо-
дель Неймана-Гейла. Положим Z
1
= Z, Γ
1
= R
n
. Если I
1
= I(Z
1
) = I, то
останавливаемся. Если же I
1
6= I, то рассматриваем подпространство Γ
2
пространства R
n
на ортах с номерами I \ I
1
. Обозначаем Z
2
= P r
Γ
2
×Γ
2
Z
1
.
Конус Z
2
является моделью Неймана-Гейла в пространстве Γ
2
× Γ
2
. Далее
мы рассматриваем ее в этом пространстве. Если I
2
= I(Z
2
) = I \ I
1
, то
останавливаемся, иначе обозначаем через Γ
3
подпространство простран-
ства R
n
на ортах с номерами I \ (I
1
∪ I
2
) и Z
3
= P r
Γ
3
×Γ
3
Z
2
. Конус Z
3
яв-
ляется моделью Неймана-Гейла в пространстве Γ
3
× Γ
3
. И так далее. Этот
процесс заканчивается на некотором шаге m. Действительно, из опреде-
ления I
j
вытекает, что I
j
6= ∅ при
j−1
S
k=1
I
k
6= I. Отсюда следует конечность
описанной процедуры и существование числа m ≤ n.
Получаем конечную последовательность непустых конусов Z
1
=
29

Z, Z
2
, . . . , Z
m
и множества индексов I
1
. . . I
m
, I
j
= I(Z
j
), I
j
∩ I
j
0
= ∅
для j 6= j
0
, при этом
m
S
j=1
I
j
= I. Из описания конструкции следует, что
каждый из конусов Z
j
представляет из себя модель Неймана-Гейла в со-
ответствующем пространстве Γ
j
× Γ
j
. Через α
j
обозначим неймановский
показатель роста этой модели Z
j
. Непосредственно из способа построе-
ния последовательности конусов Z
j
вытекает неравенство α
j
> 0 для всех
j = 1, . . . , m.
Лемма об экстремальных парах модели Z. Для любого j =
1, . . . , m и любого ε > 0 найдется такая пара (x
j
, y
j
) ∈ Z, что выполня-
ются следующие условия:
1) min
k=1...j
α
k
− min
i∈I
(y
ji
/x
ji
) ≤ ε;
2) для j < m для всех i ∈
m
S
k=j+1
I
k
выполняются равенства x
ji
= y
ji
= 0 и
для всех i ∈
j
S
k=1
I
k
выполняются неравенства y
ji
> 0. При j = m для всех
i ∈ I выполнено y
ji
> 0.
Доказательство. Зафиксируем число j < m. Пусть (ˆx
j
, ˆy
j
) - полный
неймановский процесс модели Z
j
в пространстве Γ
j
× Γ
j
. Тогда найдется
такая пара (¯x
j
, ¯y
j
) из конуса Z, проекция которой на пространство Γ
j
×Γ
j
совпадает с (ˆx
j
, ˆy
j
). Для пары (¯x
j
, ¯y
j
) справедливы неравенства ¯y
ji
> 0
для i ∈ I
j
и ¯x
ji
= ¯y
ji
= 0 для i ∈
m
S
k=j+1
I
k
. При этом выполняется условие:
min
i∈I
j
(¯y
ji
/¯x
ji
) = α
j
.
Теперь будем выбирать искомую пару (x
j
, y
j
) в виде (x
j
, y
j
) =
j
P
k=1
β
k
(¯x
k
, ¯y
k
) со специально подобранными β
1
, ..., β
j
. Пусть min
k=1,...,j
α
k
= α
l
.
Тогда выберем β
k
= 1 для k 6= l и β
l
таким большим, чтобы min
i∈
j
S
k=1
I
k
y
ji
x
ji
≥
α
l
− ε. Тогда пара (x
j
, y
j
) обладает требуемыми свойствами.
Случай j = m рассматривается аналогично с тем отличием, что некоторые
из используемых множеств оказываются пустыми. ♦
30
