Жук М.С., Молочков Ю.Б. Проектирование антенно-фидерных устройств

Подождите немного. Документ загружается.

ристики антенны. Например, КНД систем длиной

0,&к

с а/&=1,05 и а//г=1,1 примерно одинаковы, хотя

основной лепесток ДН во втором случае значительно

уже.

Это становится понятным, если сравнить коэффи-

циенты абок этих систем. В первом случае

абок —

0,25,

во

втором ~0,6

Для решеток с ^<С~з~

можно

пользоваться форму-

лами (5-54) и (5-55) для непрерывных систем с заменой

L па Nd:

(&L=

1+0

;

(A,

>=1,82^-. (5,55а)

5-3.

ЛИНЕЙНЫЕ РЕШЕТКИ С НЕРАВНОМЕРНЫМ

АМПЛИТУДНЫМ РАСПРЕДЕЛЕНИЕМ

Во многих случаях излучение антенны за пределами

главного лепестка оказывается нежелательным. С этой

точки зрения равномерные решетки не являются опти-

мальными, так как обладают довольно значительным

излучением в секторе боковых лепестков Одним из спо-

собов уменьшения бокового излучения является переход

к неравномерному

—

спадающему к краям амплитудно-

му распределению.

В принципе при этом имеется возможность выбрать

такое распределение амплитуд токов в излучателях, что

боковых лепестков вообще не будет. Таким свойством

обладают решеткисбиномиальнымраспреде-

л е

и е

амплитуд токов и с расстоянием между излуча-

телями d<Y> Для синфазных решеток d может рав-

няться Х/2; при

\\>[=/=0

d должно быть меньше Я/2.

Соотношение амплитуд токов в излучателях бино-

миальной решетки определяется той строкой в пирамиде

251

(5-60),

номер которой на единицу

телеи в решетке:

меньше числа излуча-

1 1

1 2 1

13 3 1

14 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 17 31 31 17 7 1

и т. д.

№ строчки

(5-60)

Каждую из этих решеток можно представить состоя-

щей из двух решеток, стоящих в пирамиде (5-60) строч-

кой выше, центры которых сдвинуты на расстояние

между излучателями d. Тогда по теореме умножения ДН

рассматриваемой решетки будет являться произведе-

нием ДН вышестоящей решетки на ДН системы двух

излучателей, расположенных на расстоянии, меньшем

или равном К/2 Последняя при любом ipi имеет только

один лепесток. Применяя теорему умножения и для

определения ДН вышестоящей решетки, приходим к вы-

воду, что ДН любой решетки с биномиальными ампли-

тудами токов может быть получена из ДН пары излуча-

телей, расположенных на расстоянии d<-^ и имеющих

равные амплитуды токов, путем ее возведения в степень.

Показатель степени равен номеру строки в пирамиде

(5-60),

в которой размещаются биномиальные коэффи-

циенты, определяющие распределение амплитуд токов

в излучателях рассматриваемой решетки. А так как

исходная ДН состоит из одного лепестка, то и ДН любой

«биномиальной» решетки не будет иметь боковых лепест-

ков.

Использование биномиальных решеток весьма заман-

чиво,

однако из (5-60) ясно, что при этом соотношения

токов в излучателях весьма велики. Поэтому объем,

занимаемый решеткой, используется расточительно. Для

иллюстрации сказанного на рис. 5-10 приведены ДН

линейных решеток, состоящих из пяти синфазных излуча-

телей, но имеющих различные амплитудные распределе-

ния. Эти диаграммы показывают, что биномиальная

решетка дает самую широкую ДН. По мере приближения

252

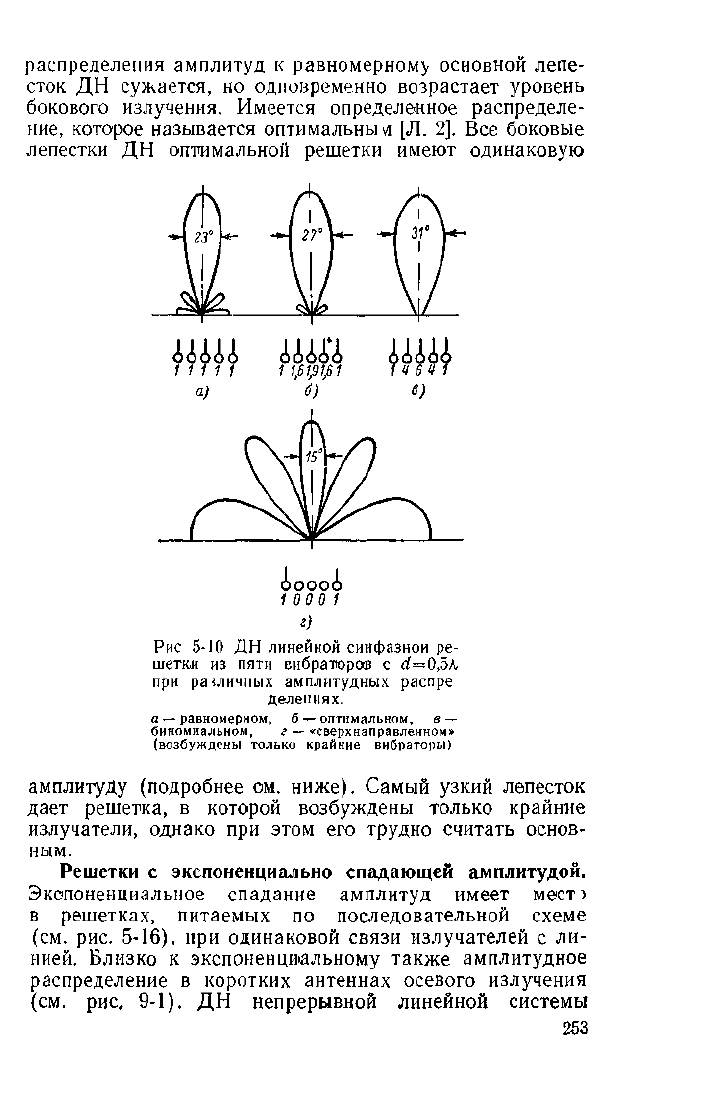
распределения амплитуд к равномерному основной лепе-

сток ДН сужается, но одновременно возрастает уровень

бокового излучения. Имеется определенное распределе-

ние,

которое называется оптимальные [Л. 2]. Все боковые

лепестки ДН оптимальной решетки имеют одинаковую

ШАА

ААШ АШ

11111 1 1,Ы,Щ1 1

6 4 1

а) 6) в)

ооооо

10001

г)

Рис 5-10 ДН линейной синфазной ре-

шетки из пяти вибраторов с d=0,5h

при ра «личных амплитудных распре

делениях.

а — равномерном, б —оптимальном, в —

биномиальном, г — «сверхнаправленном»

(возбуждены только крайние вибраторы)

амплитуду (подробнее ом. ниже). Самый узкий лепесток

дает решетка, в которой возбуждены только крайние

излучатели, однако при этом его трудно считать основ-

ным.

Решетки с экспоненциально спадающей амплитудой.

Экспоненциальное спадание амплитуд имеет мест)

в решетках, питаемых по последовательной схеме

(см.

рис. 5-16), при одинаковой связи излучателей с ли-

нией. Близко к экспоненциальному также амплитудное

распределение в коротких антеннах осевого излучения

(см.

рис. 9-1). ДН непрерывной линейной системы

253

с экспоненциально (е '

) спадающей амплитудой

определяется выражением [ЛО. 1]:

BL —

cos kL

I -г- —

cos 8)

(5-61)

/(-t--)

W '

где

— коэффициент затухания.

Для линейных решеток с <^<С~з"

можно

пользоваться

этой же формулой, полагая а = -р

L~Nd

8^-Lln^;

КНД такой системы в направлении максимального излуче-

ния определяется выражением

2<ch[!L.—

cos

^L f-г- —cos бмаьс) >

= \i

L_1_!_Z (5-62)

["•

("*"-'

;ch

—

cos

\ kL

( -r- — cos

sin

-г cos

Влияние экспоненциального спадания амплитуды вдоль

решетки проявляется в расширении основного лепестка

ДН, в увеличении бокового излучения и в заплывании

нулей в ДН. КНД с увеличением затухания уменьшает-

ся,

что справедливо как для непрерывных систем, так

и для решеток. Эти закономерности справедливы и в том

случае, если непрерывная система или решетка состоит

из направленных излучателей.

Для ориентировки в величинах, характеризующих

направленные свойства таких систем, приводим расчет-

ные данные, относящиеся к системам осевого излучения:

зависимость ширины главного лепестка на нулевом

уровне (рис. 5-11,а) и уровне 0,6 по мощности

254

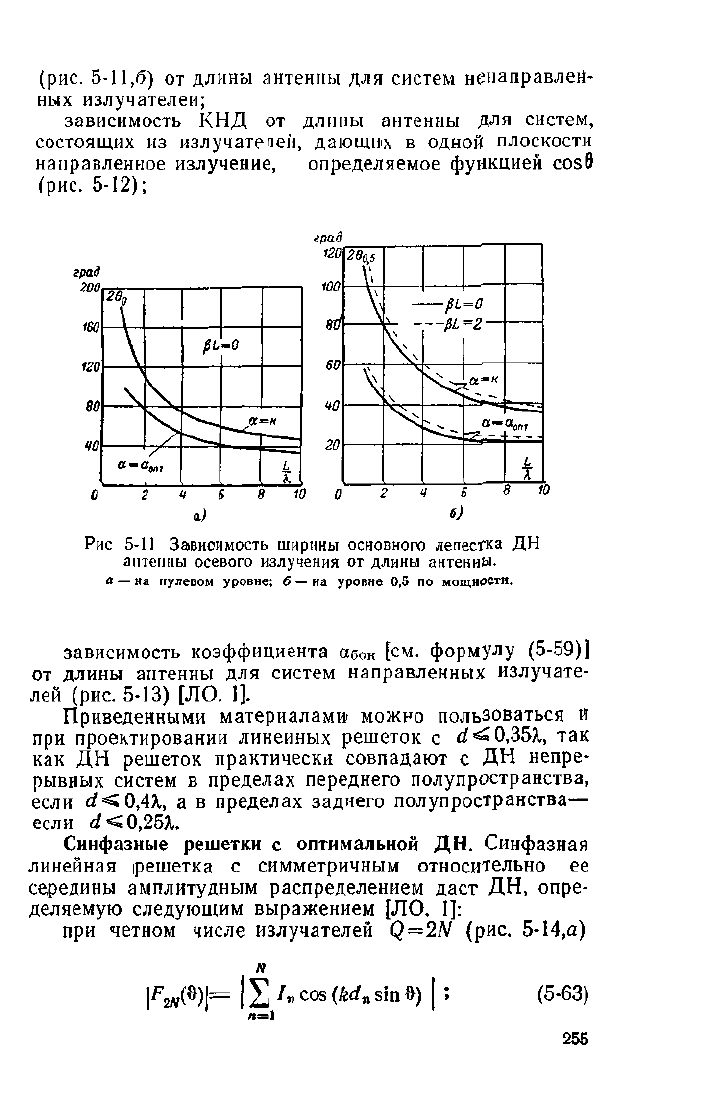
(рис.

5-11,6) от длины антенны для систем ненаправлен-

ных излучателей;

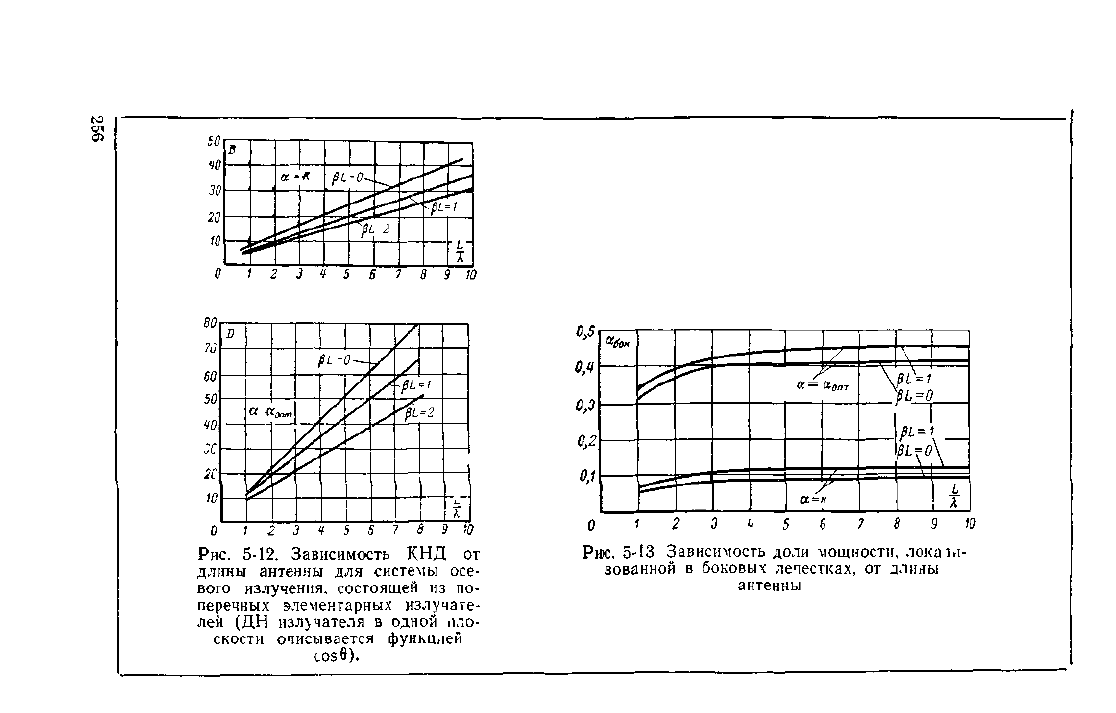
зависимость КНД от длины антенны для систем,

состоящих из излучатечей, дающих в одной плоскости

направленное излучение, определяемое функцией cos6

(рис.

5-12);

град

200

1ВО

120

во

2в

*-<*«,!

рь

*•*—.

-0

= и

ч 6

а)

10 0

Рис 5-11 Зависимость ширины основного лепестка ДН

антенны осевого излучения от длины антенны.

—

на нулевом уровне; б

—

на уровне 0,5 по мощности.

зависимость коэффициента схбок [см. формулу (5-59)]

от длины антенны для систем направленных излучате-

лей (рис. 5-13) [ЛО. 1].

Приведенными материалами можно пользоваться и

при проектировании линейных решеток с

d*£0,35X,

так

как ДН решеток практически совпадают с ДН непре-

рывных систем в пределах переднего полупространства,

если d<0,4K а в пределах заднего полупространства—

если d < 0.25А,.

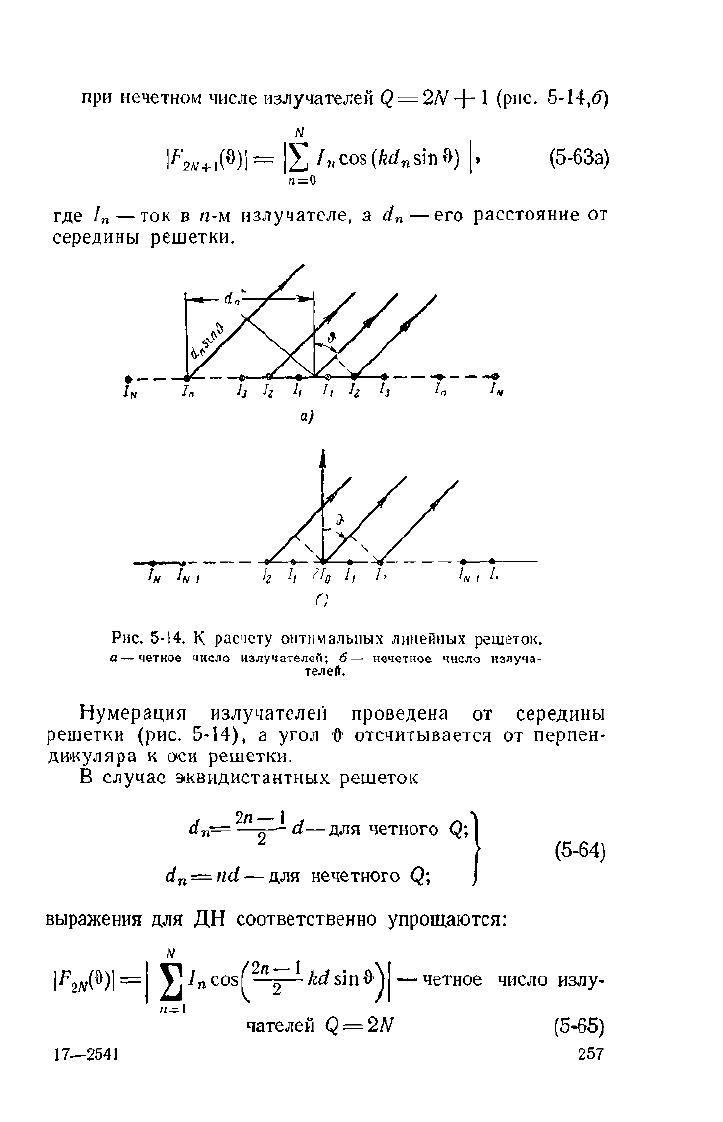
Синфазные решетки с оптимальной ДН. Синфазная

линейная решетка с симметричным относительно ее

середины амплитудным распределением даст ДН, опре-

деляемую следующим выражением [ЛО. 1]:

при четном числе излучателей

Q =

2N (рис. 5-14,а)

I^JVWH

cos

(

sin

)

(5-63)

л=1

255

СЛ

СП

fL-O-

-*?L2

^f-

1 X

/ г з ч s в 7

Рис.

5-12. Зависимость КНД от

длины антенны для системы осе-

вого излучения, состоящей из по-

перечных элементарных излучате-

лей (ДН излучателя в одной пло-

скости описывается функцией

cos

8).

-п

^опт

$1-0 —

~§L-1

•yi'2

0,5

0,4

0,3

0,2

0,1

6t>*

'—I

\ I, !

a„„

. , \

ж=о

fL = 1

pi=o\

)

Рис.

5-13 Зависимость доли мощности, локаъ

зованной в боковых лепестках, от длины

антенны

при нечетном числе излучателей

Q-=2N-{-1

(рис. 5-14,(5")

2N+№)\= Е I„cos(kd

smu) |» (5-63а)

п=й

где /„

—

ток в п-м излучателе, a d„ — его расстояние от

середины решетки.

Рис.

5-14. К расчету оптимальных линейных решеток.

—

четное число излучателе"!; б— нечетное число излуча-

телей.

Нумерация излучателей проведена от середины

решетки (рис. 5-14), а угол •& отсчитывается от перпен-

дикуляра к оси решетки.

В случае эквидистантных решеток

—=—

а—для четного Q;

/2c/

—для нечетного Q;

выражения для ДН соответственно упрощаются:

(5-64)

)I =

J]/nCOs^

-^Hsin^

чателей

п-\

17—2541

•

четное число излу-

(5-65)

257

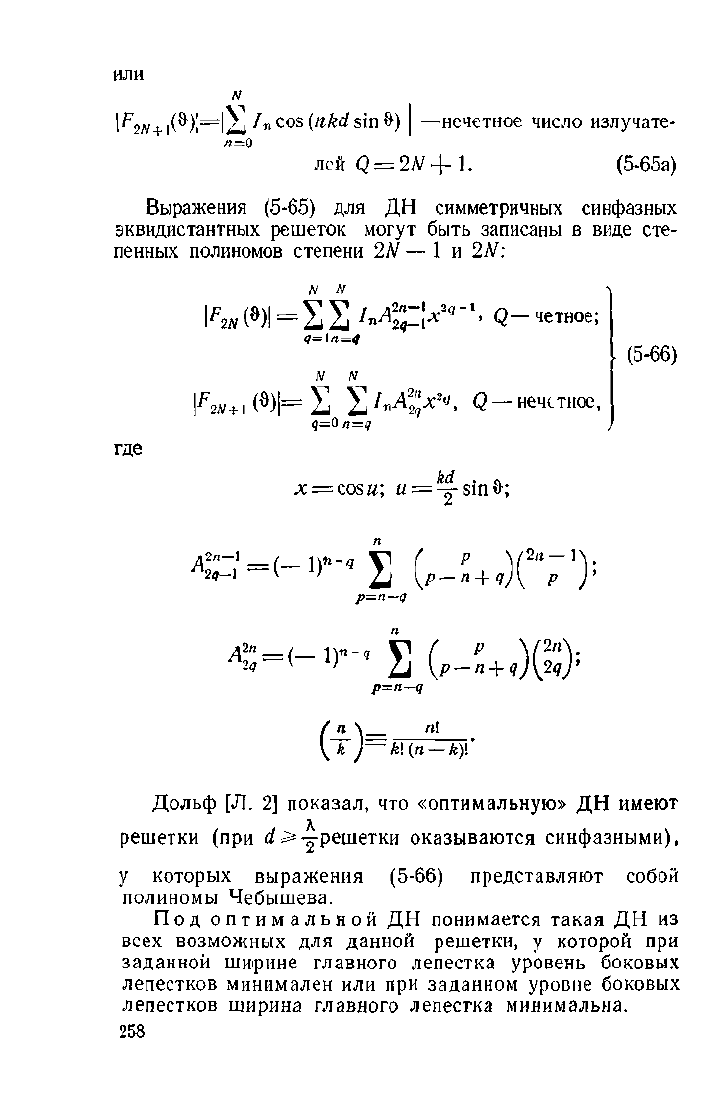
или

(9-)|=|2J/

cos(re&dsin&)

—нечетное число излучате-

ле

лей

= 2N+\.

(5-65а)

Выражения (5-65) для ДН симметричных синфазных

эквидистантных решеток могут быть записаны в виде сте-

пенных полиномов степени 2N

—

и 2N:

где

l^(

)! = SS InA^Z\x

, Q-четное;

q=0

(jr

.x;

cos«;

« = -s-sin»;

<-;=(-if-« S G_s

,)(

-')

/?=n—

•

(5-66)

= (-

(n\_

)—

k\{n

—

k)\

\(2n\

2qj'

Дольф [Л. 2] показал, что «оптимальную» ДН имеют

решетки (при £?5гурешетки оказываются синфазными),

у которых выражения (5-66) представляют собой

полиномы Чебышева.

Под оптимальной ДН понимается такая ДН из

всех возможных для данной решетки, у которой при

заданной ширине главного лепестка уровень боковых

лепестков минимален или при заданном уровне боковых

лепестков ширина главного лепестка минимальна,

258

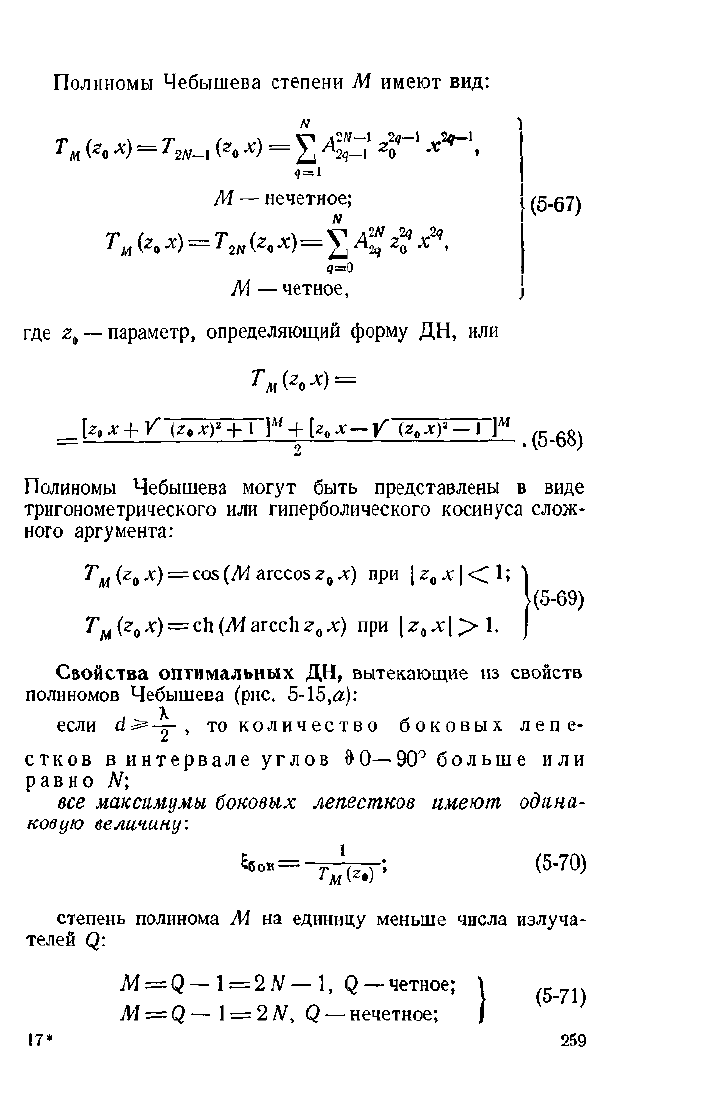
Полиномы Чебышева степени М имеют вид:

Тм (

)

' 2Л/-1 (

) — 2J 2?-1

0 •* >

4=1

Ж — нечетное;

л?

ТМ (

0 •*) = ^2« (

) = 2J ^2q

М —четное,

где z

— параметр, определяющий форму ДН, или

х)

[г,

х + / (z

xy+\~}

+[z

x-V (z

xy-\ ]

(5-67)

, (5-68)

Полиномы Чебышева могут быть представлены в виде

тригонометрического или гиперболического косинуса слож-

ного аргумента:

х)

= cos(М arccosz

х) при |г

л;|< 1;

= ch(Marcchz

x) при

|г

^|>1.

(5-69)

Свойства оптимальных ДН, вытекающие из свойств

полиномов Чебышева (рис. 5-15,а):

если dSz~Y , то количество боковых лепе-

стков в интервале углов 9 0—90° больше или

равно N;

все максимумы боковых лепестков имеют, одина-

ковую величину:

£бок = -~—7—т-; (5-70)

степень полинома М на единицу меньше числа излуча-

телей Q:

M = Q— 1=2JV — 1, Q—четное;

= Q—

= 2 N, Q

—

нечетное

17*

(5-71)

259

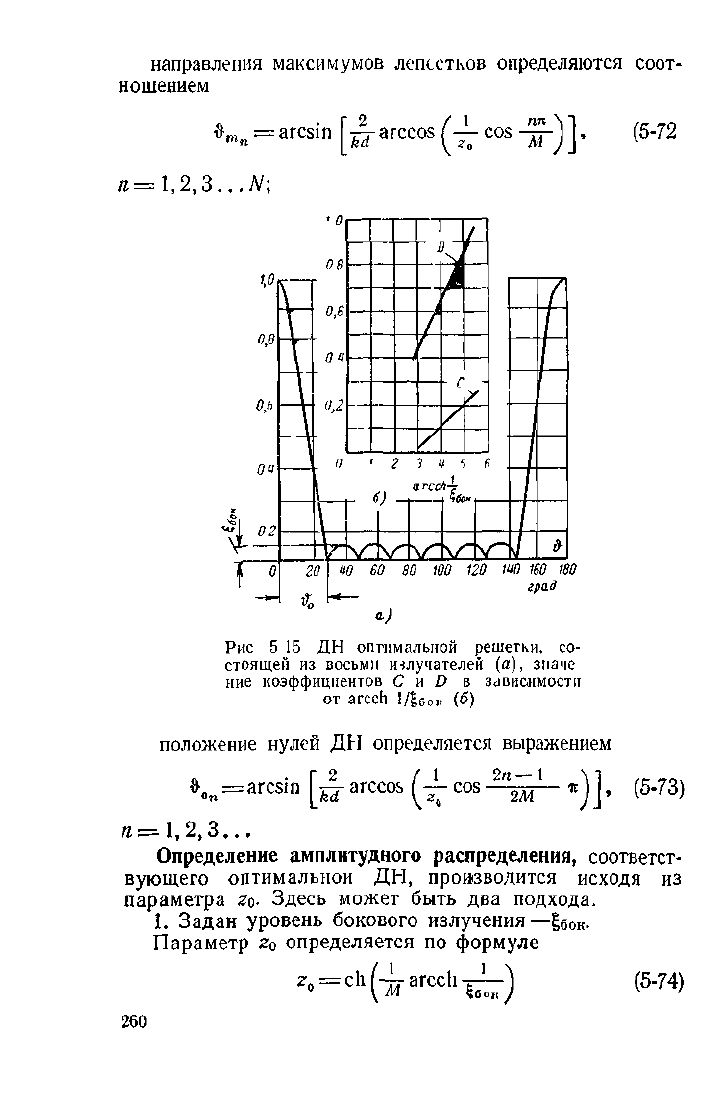
направления максимумов лепестков определяются соот-

ношением

&m„

= arcsin Г^- arccos fj- cos -Jj^-J

(5-72

«=1,2,3...JV;

20 W BO 80 100 120 140 160 180

a.)

Рис 5 15 ДН оптимальной решетки, со-

стоящей из восьми излучателей (а), значе

ние коэффициентов С и D в зависимости

от arcch

1/|бок

(б)

положение нулей ДН определяется выражением

= ^csin [A arccos (J- cos -^i- *) J, (5-73)

/i= 1,

2,3...

Определение амплитудного распределения, соответст-

вующего оптимальной ДН, проивводится исходя из

параметра Zo- Здесь может быть два подхода.

Задан уровень бокового излучения —|бок-

Параметр

определяется по формуле

ch [-гг arcch -

т)

(5-74)

260