Жук М.С., Молочков Ю.Б. Проектирование антенно-фидерных устройств

Подождите немного. Документ загружается.

имеют в ДН один главный максимум. Приводятся так-

же некоторые данные для непрерывных линейных син-

фазных систем. В тех случаях, когда эти данные отсут-

ствуют, соответствующие выражения, как и ранее, могут

быть получены из помещенных формул с помощью рас-

смотренного в § 5-1 предельного 'перехода. При этом

в формулах надо произвести замены:

Nd-+L;

(5-31)

Ширина ДН по нулям находится из общих формул

(5-23) и (5-24):

(

^=2агс8т4~; 28^

2 -г- при L >Я;

,(А?)

2arcsin4i ;2fJ^~2^npn Nd>l.

\ (5-32)

Здесь и ниже значком L отмечаются величины, отно-

сящиеся к непрерывным системам, а значком N— к ре-

шеткам, 'состоящим из N излучателей.

Ширина ДН на уровне 0,5 мощности находится по

формулам:

26<>=2arcsin(^\ 26$* 0,884-

рад

50,8°

при L > Я;

V5~

Ы Nd'

(5-33)

Коэффициент A

находится с помощью решения транс-

цендентного уравнения (5-26) при 5=1 и подстановки его

решения в формулу (5-25). Для

с£

= 0,5Я (fed =

it)

значе-

ния коэффициента А

приведены в табл. 5-2.

а б

л и ца 5-2

Micro излучателей, N

16—2541

54,3

52,6

51,6

50,97

241

Данные таблицы показывают, что даже при сравнительно

большом расстоянии между излучателями, равном Я/2, при

Л/'>4 коэффициент A

отличается от значения аналогич-

ного коэффициента в формуле для непрерывной системы

меньше чем на 5°/

. Поэтому при iV>4 и d<-g- с доста-

точной для практики точностью 26

(

g можно определять

по формуле (5-33) для 26^. То же самое можно сказать и

об уровне боковых лепестков (см. табл. 5-1), но при усло-

вии

> 10.

КНД определяются выражениями:

iL)

--=-

2s in

—

Si (kL)

{N)

/V—1

1+2

n = \

sin (nkd)

nkd

(5-34)

Реальные решетки всегда состоят ив направленных

излучателей, поэтому для каждой из них нужно опре-

делять КНД по общим формулам, приведенным в §2-8.

Для линейной непрерывной системы и решетки, со-

стоящих из элементарных вибраторов, оси которых сов-

падают с осью решетки, КНД определяются выраже-

ниями [ДО. 27]:

,<£>_

(Л>)_

„Го,

,,,, coskL — 2 , sin kL

[

SI(

£)

+—*z"+w

л?—1

. (5-35)

cos(nkd) sin (nkd)

(nkd)

)

При постоянном расстоянии между излучателями КНД

растет примерно пропорционально длине антенны

(рис.

5-6,6). Если же зафиксировано число излучателей,

а меняется расстояние между ними, то существует опти-

мальное d, при котором КНД достигает максимума

242

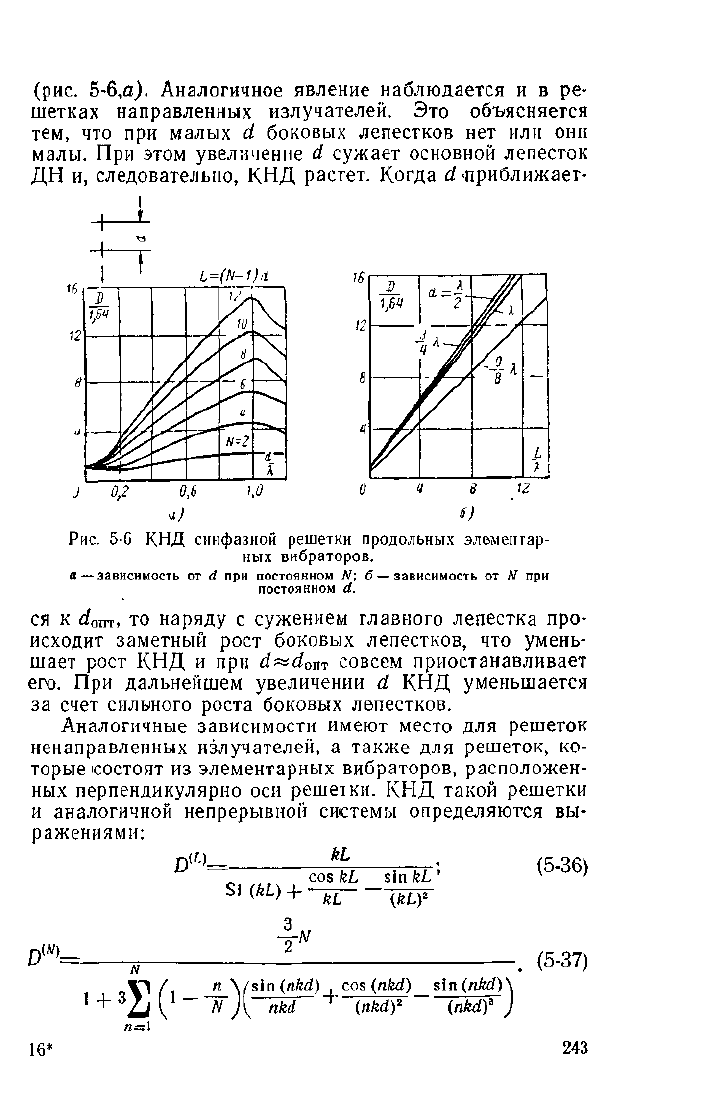
(рис.

5-6,а). Аналогичное явление наблюдается и в ре-

шетках направленных излучателей. Это объясняется

тем, что при малых d боковых лепестков нет или они

малы. При этом увеличение d сужает основной лепесток

ДН и, следовательно, КНД растет. Когда d ириближает-

L=(N-1),1

1,6V

N=2

1,61 2

; А

МГ^

J 0,2

0,6 ',0 О Ч 6

а) 6)

Рис.

5-G КНД синфазной решетки продольных элементар-

ных вибраторов.

—

зависимость от d при постоянном N; б

—

зависимость от N при

постоянном й.

ся к с?опт, то наряду с сужением главного лепестка про-

исходит заметный рост боковых лепестков, что умень-

шает рост КНД и при d~d

m совсем приостанавливает

его.

При дальнейшем увеличении d КНД уменьшается

за счет сильного роста боковых лепестков.

Аналогичные зависимости имеют место для решеток

ненаправленных излучателей, а также для решеток, ко-

торые состоят из элементарных вибраторов, расположен-

ных перпендикулярно оси решетки. КНД такой решетки

и аналогичной непрерывной системы определяются вы-

ражениями:

->('-)

^ .

Si (kL) +

cos kL sin kL '

(5-36)

(Щ

-/v

sin (nkd) . cos (nkd)

nkd

(nkd)

sin(nkd)\

(nkd)

(5-37)

243

Для рассмотренных решеток оптимальные расстояния

имеют следующие величины:

с?опт~0,5А

—

при изотропных излучателях;

й?опт~А

—

при продольных элементар- "j

ных вибраторах; I (5-38)

)

(0,7-^0,9)Я

—

при поперечных элементар-

ных вибраторах.

Если

d=d

our

и L>A, то формулы для КНД прини-

мают простой вид:

iN)

2 -ч изотропные излучатели;

D'^W-^-

-j-

-JT

продольные элементарные

вибраторы;

'=-2—[-

-j-

поперечные элементарные

вибраторы.

Для синфазных линейных решеток с d =

для КНД также значительно упрощаются:

(5-39)

выражения

D ' = N =•

-г-

-j-

1—для

изотропных излучателей;

3/V

Л/—1

+ 6

Ж-*)

(-1)"

iN)

ZJ[

Nj (Л*)» )

— 3

-для продольных вибрато-

ров;

(5-40)

—

для поперечных вибра-

торов.

Приведенные формулы могут быть использованы и

для расчетов КНД решеток симметричных вибраторов,

длина 'которых не превосходит А./2, так как при этом

ДН симметричного вибратора мало огличается от ДН

элементарного вибратора.

Равномерные решетки с осевым излучением имеют

в ДН один главный максимум нулевого порядка. Условии

получения осевого излучения при этом имеют вид:

Ф.

•-k —

для непрерывных систем;

э kd

—

для решеток.

(5-41)

244

Это означает, что здесь У

СР

<С; следовательно, это

системы (решетки) с замедлением.

Для получения одного максимума расстояние между

излучателями решетки должно быть меньше определен-

ной величины, с тем чтобы удовлетворялось неравенство

ил»

* Ы ^- d

(5-42)

Это расстояние зависит от эквивалентного замедле-

ния фазовой скорости, равного

^\/kd,

для решеток, у ко-

торых

Ф,

= М; й!

акс =

-2--

(5-43)

С возрастанием замедления

waKC

уменьшается. График

зависимости

MaK

от tyjkd приведен на рис. 5-7.

Ширина ДН на нулевом уровне определяется по ниж-

ней формуле (5-23). Для длинных антенн можно в пределах

главного лепестка считать, что cos

яг

—~~, тогда фор-

мула (5-23) примет вид:

26«4«2l/2i/—(-J--1) [рад];

(5-44)

Из этих выражений очевидно, что для антенны осево-

го излучения зависимость ширины ДН от относитель-

ной длины ангенны L/X более слабая, чем для синфаз-

ной антенны.

Поэтому одиночные антенны осевого излучения не-

целесообразно 'применять для получения узких ДН.

Соотношения (5-44) показывают, что при увеличении

отношения а/к (или -tyi/kd) можно безгранично сузить

ДН. Однако, как выше было показано, одновременно

с сужением главного лепестка возрастают максимумы

других лепестков. КНД с ростом а/k сначала увеличивает-

ся,

а затем резко падает. Оптимальное отношение а/к

245

(или т|3]/Ы) при £L>

(#Ы> 1 и Ы<1) йМебт вели-

чины:

=1 +

2.94, )

~ТГ''

2,94

Nkd'

(5-45)

При оптимальном замедлении ширина основного лепе-

стка на нулевом уровне оказывается равной:

2f)'

£)

~2,06j/A;

(5-46)

Таким образом, увеличение замедления от единицы

(a =

k) до оптимального уменьшает ширину главного ле-

пестка на нулевом уровне примерно в 1,4 раза.

и,ь

4,3

0,2

0 /

ймамс^***

' Л

ч»

Рис 5-7. Зависимость максимального

расстояния между излучателями от ча

медления D решетке осевого излучения,

при котором ДН все еще имеет только

один главный максимум

Ширина основного лепестка на уровне 0,5 по мощно-

сти определяется по формуле (5-28). При a=k, хо,5=1,39,

а при а = а

пг, хо,5=

1,945.

Подстановка в формулу (5-28)

этих значении приводит к выражениям:

26^= 2arccos(

•—~J при

= k;

26^=2arccosM ~\ при а=а

оП

246

(5-47)

Для длинных систем можно пользоваться приближенными

формулами:

20^»

1,881/-£-

при

} (5-48)

2fj

UOJ/ ~ при <x=a

0IlT

. j

Таким образом, увеличение замедления до оптималь-

ного сужает ДН на уровне половинной мощности при-

мерно в 1,7 раза, т. е. значительно сильнее, чем на ну-

левом уровне.

Это объясняется тем, что при увеличении замедле-

ния основной лепесток заостряется (см. рис. 5-5).

В случае дискретной решетки величина x

0i5

зависит

также и от N, поэтому йаписать выражение для

</V)

в общем виде невозможно. В случае малых kd и боль-

ших N, когда в пределах главного лепестка можно по-

ложить:

sin (kd cos

—

<]>!)»*

kd cos

б — <J»„

(549)

для определения 26^ можно пользоваться формулами (5-47)

и (5-48), заменив в них L и Nd. Для случая d==— эти

формулы принимают вид:

ойМ

л 215,5° Ф, , 1

26„,*» —= рад=-—-=- при — =

для

-5~-

(

°)

ой(

1) 2,2 , 126° Ф, /Ф, \

26*

;* —= рад=-

=. при ^ = (—

]

}

При

i])i

= ftd величины боковых максимумов ДН такие

же,

как и у синфазной решегки (формулы (5-Ю) и

(5-П)].

В решетке с замедлением значение F (0) умень-

шается, и поэтому относительные уровни боковых лепе-

стков растут. В случае непрерывных систем с оптималь-

ной фазовой скоростью, а также для решеток, у которых

в пределах основного лепестка можно считать

sini|7~i|;, F(0) —0,677. При этом максимумы боковых

лепестков по мощности возрастают в 2,18 раза. Мак-

симум первого бокового лепестка по мощности! возра-

стает до 10,8% максимума главного лепестка.

КНД равномерной линейной решетки с осевым изле-

чением определяется по формулам (5-29) и (5-30). В ча-

247

стном случае

= ^(jdi —* )

после

ние

принимают вид:

(W)

я=1

при

<!>!

= &d;

/г "\sin (Inkd)

nkd

iL)

Si (2ftL)+

cos 2/feZ, — 1

2ftZ

при

— k.

(5-51)

Для достаточно длинных систем

(

4L .

-у- при а =;

(5-52)

Для решетки с излучателями, расположенными на

расстояниях d

X/4:

£)W«iV при 1|л = М.

(5-53)

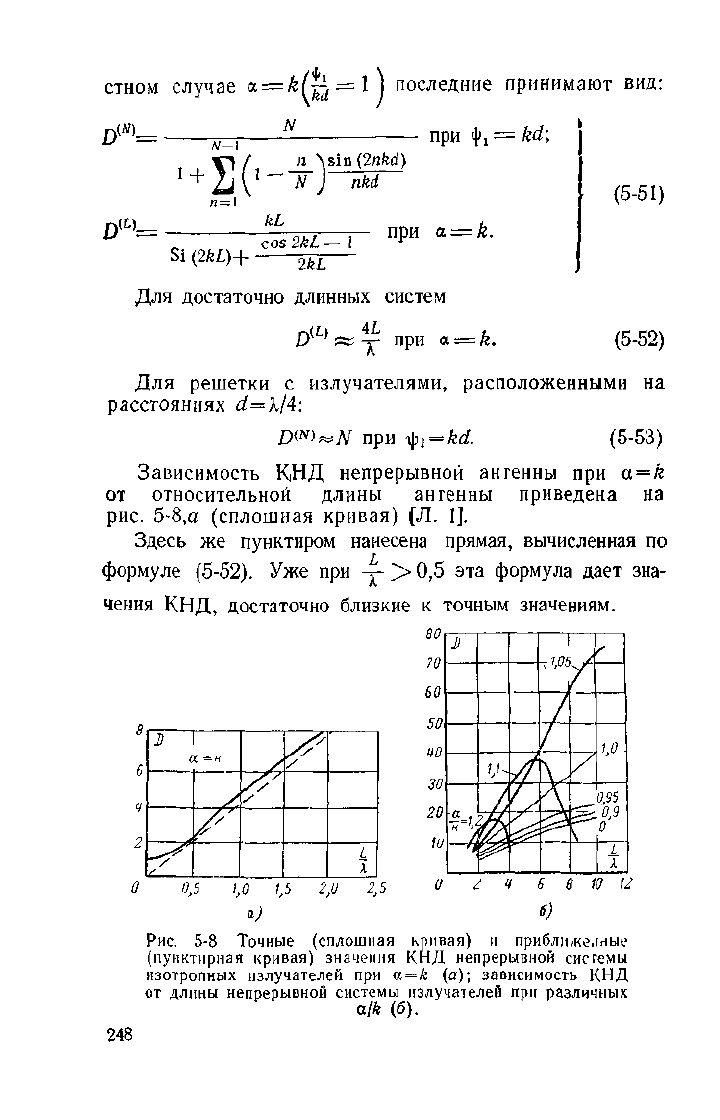
Зависимость КНД непрерывной ангенны при

<х

/е

от относительной длины ангенны приведена на

рис.

5-8,а (сплошная кривая) [Л. 1].

Здесь же пунктиром нанесена прямая, вычисленная по

формуле (5-52). Уже при -д~>0,5 эта формула дает зна-

чения КНД, достаточно близкие к точным значениям.

го

1и

-J?

/у

{У

уГУ

/У

уУу

/у

])

^ч

V-

?/•£.

105 X

\,у

,о

0,95

^ 0,9

\ °

0,5 1,0 1,5

а)

2,0

2,5

10 12

Рис.

5-8 Точные (сплошная кривая) и приближенные

(пунктирная кривая) значения КНД непрерывной системы

изотропных излучателей при a—k (а); зависимость КНД

от длины непрерывной системы излучателей при различных

а/к (б).

248

Зависимости КНД непрерывной системы от относитель

ной длины антенны при различных отношениях a/k приве

дены на рис.

5-8,6.

При

0<~<1,

т. е. в антеннах

с ускорением, КПД (при -у->• 0,3

—

0,5) линейно свя-

зан с Ljl, при этом чем больше a/k, тем больше КНД

при данной длине антенны. В этом случае КНД прибли-

женно можно определить по формуле

при-^-<1,

(5-54)

где коэффициент А лежит в пределах 0,5 < А

<•

и зави-

сит от а//г; при -^-< 0,8

—

0,9 он близок к 0,5 при

-^—»-1;

В антеннах с замедлением (а > k) КНД достигает для

заданного a/k максимума при некоторой относительной

длине (L/A.)

OI]T

. Графики, приведенные на рис. 5-8,6 для

-г->1,

показывают, что

{L/l)

0Ilr

быстро падает с увели-

чением замедления. Это ограничивает возможное увеличе-

ние КНД по сравнении с незамедленной антенной (а = £).

Физика этого явления рассмотрена ранее (см. рис. 5-5).

Величина оптимального замедления связана с дли-

ной антенны соотношением (5-45), которое можно запи-

сать в виде

(т)„„=

+°-

468

Г- (5-55)

Для коротких антенн численный коэффициент в этой

формуле должен быть увеличен до 0,5. Чем длиннее

антенна, тем меньше оптимальное замедление.

Для антенн с оптимальным замедлением КНД можно

вычисли7ь по формуле (5-54), причем коэффициент А

имеет следующие значения:

при

0,3

< 4-<

0,5;

А =1,82 при —> 0,5; } (5-56)

Л=1 при-=- -оо.

249

Для равномерной линейной системы, состоящей из по-

перечных токов (этот случай близок к применяемым на

практике антеннам осевого излучения), при оптималь-

ном замедлении справедливо соотношение

В такой антенне может быть достигнут следующий

максимальный КНД (при а = а

0П

т):

Я ^ 2,7 + Л ~, (5-58)

где

=2,1.

Полезной характеристикой антенны является коэф-

фициент абок, показывающий, какая доля излучаемой

мощности попадает в боковые лепестки ДН:

«бок = ^-

. (5-59)

На рис. 5-9 приведены зависимости абок от длины антен-

ны при различных замедлениях: они показывают, как

резко растет мощность, теряемая в боковых лепестках,

с увеличением замедления. При "r^l в боковые ле-

пестки попадает ~ 10% мощности; при оптимальном за-

медлении уже 50% мощности рассеивается на боковое

излучение.

Графики, приведенные на рис. 5-8 и 5-9, позволяют

проследить влияние изменения формы ДН на характе-

2 Ц 6 8 10 1Z

Рис.

5 9 Доля мощности, локализо-

ванной в боковых лепестках, в зави-

симости

о г

длины антенны при раз-

личных замедлениях ujk.

250