Zhu J. Applications of Fourier Transform to Smile Modeling: Theory and Implementation

Подождите немного. Документ загружается.

48 3 Stochastic Volatility Models

lution which allows for a correlation between stock returns and variance and even

admits multiple lags in the GARCH process. However, since we focus on contin-

uous time valuation in this book, econometric models will not be in consideration

here.

3.2 The Heston Model

3.2.1 Model Setup and Properties

The Heston model (1993) is the ﬁrst stochastic volatility model that systematically

deal with the valuation of options with CFs and provides a quasi closed-form solu-

tion for options. Heston does not model stochastic volatility directly, but stochastic

variance. In this section, we denote V(t)=v

(t) as variance. The risk-neutral Heston

model consists of the following two processes

dS(t)

S(t)

= rdt +



V(t)dW

(t), (3.3)

dV(t)=

(

−V(t))dt +



V(t)dW

(t),

(t)dW

(t)=

dt.

The process specifying the variance is identical to the one that Cox-Ingersoll-Ross

apply to model short interest rates, and is called mean-reverting square root process.

The mean-reversion is a desired property for stochastic volatility or variance and is

well documented by many empirical studies. The parameter

marks the long-term

level that variance gradually converges to. The parameter

controls the speed of

variance’s reverting to

. The parameter

is refereed to as the volatility of variance

since it scales the diffusion term of variance process.

As noted by Heston, the volatility v(t) in the Heston model initially follows an

Ornstein-Uhlenbeck process with a mean-reverting level as zero, that is

dv(t)=−

v(t)dt +

(t). (3.4)

To obtain a risk-neutral process for variance, a market price of volatility risk

must be intro-

duced, which depends on the assumption about the risk aversion. A common way to determine

is to assume

dt =

Cov[dv, dC/C] where

and C is the relative-risk aversion and consumption

respectively. From the well-known Cox, Ingersoll and Ross (1985a) equilibrium model, one can

get a consumption process [also see equation (8) in Heston]:

dC =

V(t)Cdt +



V(t)CdW

(t).

Consequently, the risk premium is proportional to V (t),

(V )=

V with

a constant. With the

adjustment, the original process and adjusted process have the same structure.

The true volatility of variance should be



V(t) since it is the coefﬁcient of the diffusion term.

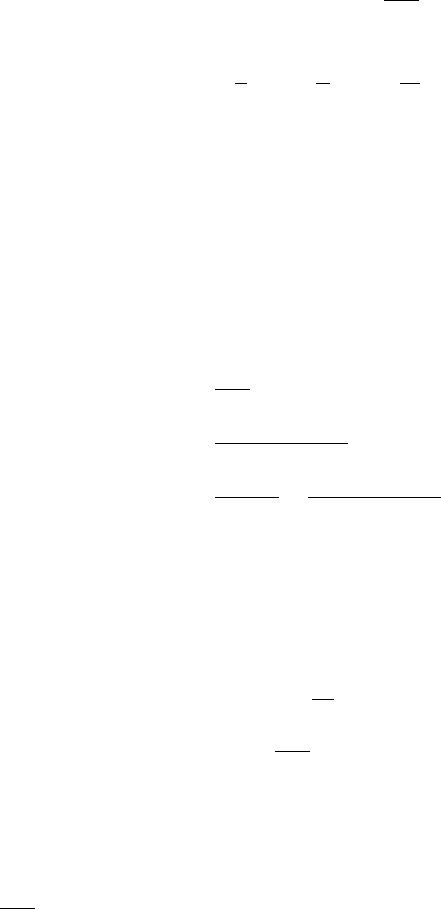
3.2 The Heston Model 49

So by applying It

o’s lemma, the square of volatility V(t)=v

(t), namely the vari-

ance of the instantaneous stock return, follows a square-root process which is given

dV(t)=

[

−V(t)]dt +



V(t)dW

(t) (3.5)

with

. (3.6)

and

satisfy the following conditions,

κθ

, V

> 0, (3.7)

it can be shown that variances V (t) are always positive and the variance process

given in (3.5) is then well-deﬁned under above condition. The condition (3.7)is

also referred to as Feller’s condition for square root process. Let

(x,d,n) denote

a non-central chi-square distribution with d as the degrees of freedom and n as

non-centrality parameter. The variance V(t) conditional on V (s) is distributed as a

non-central chi-square distribution F

(aV (t), d, n) where

d =

κθ

n =

−

(t−s)

(1−e

−

(t−s)

)

a =

−

(t−s)

(1−e

−

(t−s)

)

Based on the properties of a non-central chi-square distribution, V (t) has the fol-

lowing two conditional moments,

E[V(t)|V (s)] =

+(V (s)−

−

(t−s)

, (3.8)

Var[V (t)|V (s)] = V(s)

−

(t−s)



1 −e

(t−s)





1 −e

(t−s)



. (3.9)

As mentioned above, the positive values of the square root process can be only guar-

anteed under the condition (3.7) which unfortunately is not always given in practi-

cal applications. Even under the condition (3.7), if we simulate a mean-reverting

square root process, it is very possible to generate some negative paths due to the

nature of Monte-Carlo simulation, and the negative V (t) makes the computation of



V(t)dW

(t) impossible and leads to error. Hence, a satisfactory simulation of the

mean-reverting square root process is a challenging issue in computational ﬁnance.

We will return to this issue in Chapter 5 with more detailed discussions.

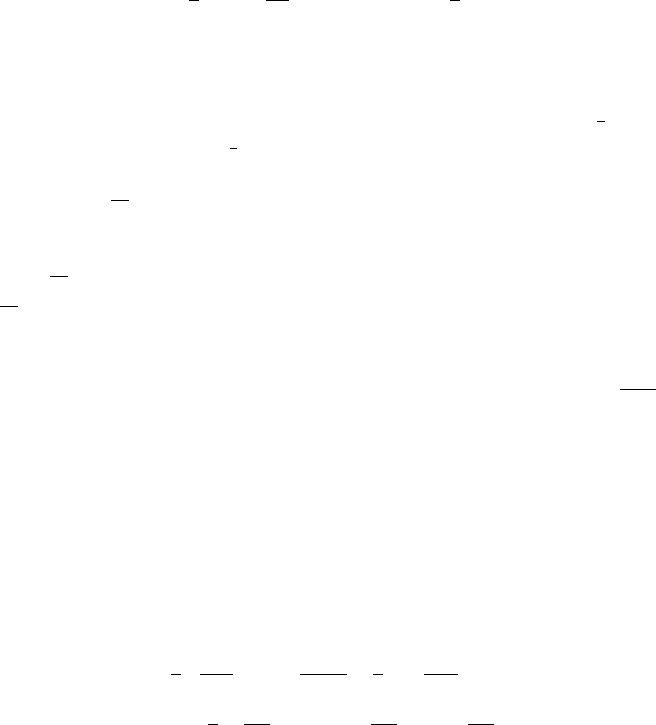
50 3 Stochastic Volatility Models

Again applying It

o’s lemma, we obtain the following stochastic process for the

volatility v(t) from the variance V(t),

dv(t)=



(

−

−1

(t) −v(t)



dt +

(t). (3.10)

Obviously, with the parameter setting given in (3.6), the above process is reduced

to an Ornstein-Uhlenbeck process with zero mean level. Compared with the pro-

cess of V(t) given in (3.5), we can observe that the process of v(t) perseveres the

mean-reversion structure. However, the mean-reversion speed of v(t) is

, and

the volatility of volatility is

, equivalent to the half value of the corresponding

variance process V(t). More worthy to mention is the mean level of v(t) which

−

−1

(t) − v(t). Firstly, the mean level

is not deterministic as

for variance, but stochastic. This means we can not expect the volatility will con-

verges to a given value in the Heston model. Secondly,

has two terms

−1

(t)

and −

−1

(t). While the ﬁrst term

−1

(t) is of a order of v(t), the second term

−1

(t) could be very large. These two effects together makes the mean level of

volatility in the Heston model could be very small, even negative. The condition

that

keeps positive is 4

κθ

. Obviously, Feller’s condition (3.7) for positive

variance V(t) is sufﬁcient for a positive mean level of volatility v(t) in the Hes-

ton model. For more discussions on the properties of the density of v(t)=



V(t),

please see Lipton and Sepp (2008).

3.2.2 PDE Approach to Pricing Formula

Now we demonstrate the original approach with which Heston has derived his pric-

ing formula. Based on the risk-neutral processes in (3.5), we can apply the Feynman-

Kac theorem and derive a two-dimensional pricing PDE for option as follows:

∂

ρσ

∂

(r −

∂

(

−V)

∂

−rC =

∂

, (3.11)

where x(t)=lnS(t) and T is the maturity of the option. To obtain a closed-form

pricing formula for European-style options in the Heston model, we suggest that the

searched formula takes a same form as in the Black-Scholes formula, that is

= S

−Ke

−rT

where F

,i = 1,2, are two exercise probabilities under the respective measures.

Inserting this equation into the PDE (3.11) yields two PDEs for F

and F

re-

spectively. This ﬁrst one is

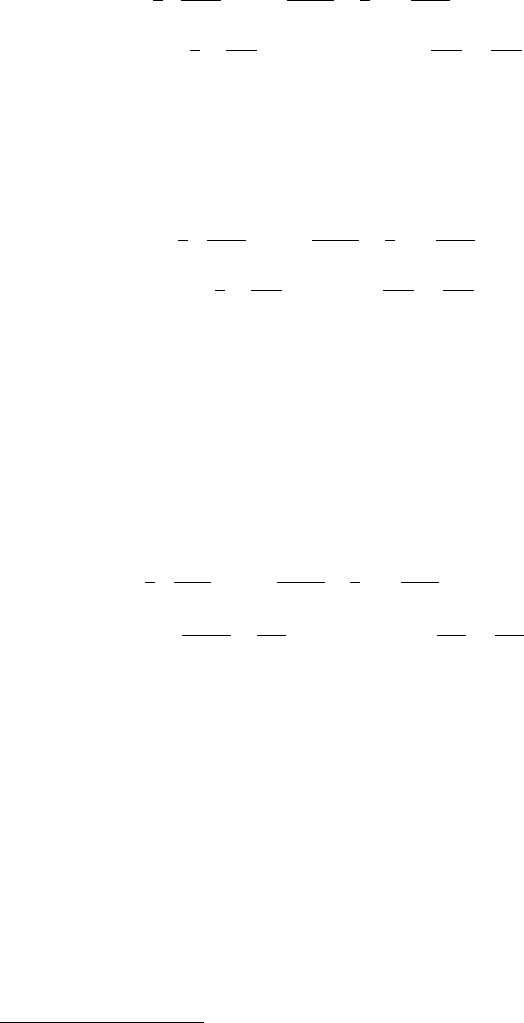
3.2 The Heston Model 51

∂

ρσ

∂

(r +

∂

(

−V)+

ρσ

∂

(3.12)

with a boundary condition

)=1

>lnK)

The second PDE is

∂

ρσ

∂

(r −

∂

(

−V)

∂

(3.13)

with a boundary condition

)=1

>lnK)

This means that two exercise probabilities satisfy a similar PDE as the one for

call price. According to Kolmogorov’s backward equations, a moment-generating

function must satisfy the same PDE as its probability, but with different boundary

condition. Since the characteristic function is a special case of moment-generating

function, we have two PDEs for the CFs f

(

), j = 1,2,

∂

ρσ

∂

(r −

(−1)

∂

(

−V)+a

]

∂

, (3.14)

where a

ρσ

V and a

= 0. The boundary conditions are

,T = 0)=exp(i

), j = 1,2.

We propose a guess for the solution for f

which takes the following exponential

form

(

,T)=exp



+ rT) −s

2 j

κθ

T)+H

(T)V

+ H

(T)



= exp



+ rT)



Heston

(

) (3.15)

with

Heston

(

)=exp



−s

2 j

κθ

T)+H

(T)V

+ H

(T)



. (3.16)

By plunging this guess into the PDE in (3.14), we can arrive at two different

ODEs for H

and H

. Solving these ODEs yields the following functions,

The proposed solution here is a bit different from the Heston’s original one.

52 3 Stochastic Volatility Models

(T)=



2 j

(1+e

−

) −(1 −e

−

)(2s

1 j

2 j

)



(T)=

κθ



exp(

(

−

)T)



, (3.17)



+ 2

1 j

= 2

−

2 j

)(1−e

−

For the ﬁrst CF f

, we have the parameters s

and s

= −(1 + i

)



ρκ

−

(1+i

)(1−

)



=(1 + i

)

Similarly for the second CF f

,wehaves

and s

= −i



ρκ

−

(1−

)



= i

Note the above expressions for CFs are not identical to Heston’s original ones. It

can be shown that the both expressions are equivalent.

3.2.3 Expectation Approach to Pricing Formula

As shown above, Heston’s original method is to derive CFs via two-dimensional

PDEs. But the derivation of a closed-form solution by solving a PDE is generally

not a trivial task, and can not be always successful. Here we present an alternative

and more general way to obtain the same closed-form solution for CFs in the Heston

model. Namely, we calculate CF directly by reducing two-dimensional problem into

one-dimensional problem. Zhu (2000) has shown this method in details. Now let us

consider the ﬁrst CF.

(

)=E

(T)exp(i

x(T))] = E

[exp(−rT −x

+(1 + i)

x(T))]

= exp[i

+ rT)]

× E



exp



(1+i

)



−



V(t)dt +





V(t)dW

(t)





Decomposing W

into two parts



1 −

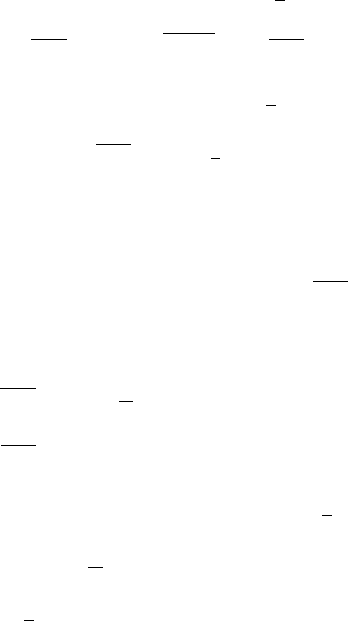
3.2 The Heston Model 53

where W is not correlated with W

and W

. Now we can rewrite the above equation

(

)=exp[i

+ rT)]E



exp



(1+i

)



−



V(t)dt





V(t)dW

(t)+



1 −





V(t)dW(t)





= exp[i

+ rT)]E



exp



−(1+ i

)



V(t)dt

+(1 + i

)





V(t)dW

(t)+

(1−

)(1+i

)



V(t)dt



(3.18)

At the same time, we integrate V (t) and obtain

V(T ) −V

κθ

T −



V(t)dt +





V(t)dW

(t).

Rearranging this equation yields





V(t)dW

(t)=



V(T ) −V

−

κθ

T +



V(t)dt



By inserting





V(t)dW

(t) into (3.18)wehave

(

)=exp[i

+ rT)]E



exp



−(1+ i

)



V(t)dt

+(1 + i

)



V(T ) −V

−

κθ

T +



V(t)dt



(1−

)(1+i

)



V(t)dt



= exp[i

+ rT) −s

κθ

T)]

× E



exp



−s



V(t)dt + s

V(T )



, (3.19)

where s

and s

are already given above.

So far we have changed the two-dimensional expectation into a one-dimensional

expectation where S(T) has vanished. To obtain the ﬁnal form of f

(

), we need

only to calculate the following expectation

y(V

,T)=E



exp



−s



V(t)dt + s

V(T )



. (3.20)

According to the Feynman-Kac theorem, the expected value y(V

,T) should fulﬁll

the following one-dimensional PDE,

54 3 Stochastic Volatility Models

∂

= −s

Vy+

(

−V)

∂

(3.21)

with a boundary condition

y(V

,0)=exp(s

We can show easily that the solution to this PDE is

y = exp(H

(T)V

+ H

(T)), (3.22)

where the functions H

(T) and H

(T) are given in (3.17). Plunging the solution of

y into f

(

) yields the analytical solution of the ﬁrst CF f

(

The above procedure shows the basic idea of the expectation approach: the di-

mension reduction via stochastic calculus. Finally we only need to solve a one-

dimensional PDE instead of two two-dimensional PDE in a straightforward PDE

approach. The derivation of f

(

) follows exactly the same way.

3.2.4 Various Representations of CFs

The CFs derived above are one of some representations in ﬁnancial literature. In fact,

the original CFs given in Heston (1993) take an other form. For readers’s reference,

we give the original Heston’s representation as follows:

Heston

(

)=exp



∗

(T)V

+ H

∗

(T)



, j = 1,2, (3.23)

with

∗

(T)=

+ d

−

ρσ



1 −e

1 −g



, (3.24)

∗

(T)=

κθ



+ d

−

ρσ

)T −2ln



1 −g



, (3.25)

where

+ d

−

ρσ

−d

−

ρσ



(

ρσ

−b

)

(

−i



(

ρσ

−b

)

(

+ i

−

ρσ

, b

Straightforward but involved calculation can verify that H

∗

(T) is equal to H

(T)+

2 j

, and H

∗

(T) is equal to H

(T)+s

2 j

κθ

T in (3.15).

3.3 The Sch

obel-Zhu Model 55

A similar representation of CFs is given by Schoutens-Simons-Tistaert (2004)

and Gatheral (2005), which reads

∗

(T)=

−d

−

ρσ



1 −e

1 −q

−d



(3.26)

and

∗

(T)=

κθ



−d

−

ρσ

)T −2ln



1 −q

−d

1 −q



(3.27)

with

= 1/g

To verify the equivalence between these two representations, we just utilize the fol-

lowing facts,

+ d

−

ρσ



1 −e

1 −g



+ d

−

ρσ



1 −e

−d

1 −e

−d



−d

−

ρσ



1 −e

1 −q

−d



and

T −2ln



1 −g



= d

T −2ln



−d

−g

)

1 −g



= d

T −2d

T −2ln



−d

−1)

1/g

−1



= −d

T −2ln



(1−q

−d

)

1 −q



At a ﬁrst glance the difference between two representations is very small.

However, as discussed in Albrechter-Mayer-Schoutens-Tidtaert (2006), Roger-Kahl

(2008), with the small modiﬁcations von H

∗

(T) in (3.26) and H

∗

(T) in (3.27) pos-

sible discontinuity of the CFs in the Heston model can be circumvented. We will

discuss this topic in details in Chapter 4.

3.3 The Sch

obel-Zhu Model

3.3.1 Model Setup and Properties

Besides the mean-reverting square root process in the Heston model, a mean-

reverting Ornstein-Uhlenbeck process is an other popular process in ﬁnancial mod-

eling. The ﬁrst short interest rate model, Vasicek model (1973), is based on a mean-

56 3 Stochastic Volatility Models

reverting Ornstein-Uhlenbeck process. Generally, compared with a mean-reverting

square root process, a mean-reverting Ornstein-Uhlenbeck process is Gaussian and

has nice analytical tractability. Many ﬁnancial economists applied also the mean-

reverting Ornstein-Uhlenbeck process to model stochastic volatility, for example,

Wiggins (1987), Stein and Stein (1991). Stein and Stein derived a quasi-closed form

solution for option where the underlying asset S(t) and its volatility v(t) are not cor-

related. As we know, the volatility skew is mainly caused by the correlation between

the underlying asset and its volatility. Therefore with respect to the correlation, Stein

and Stein’s solution is very restrictive and is not able to explain the most smile ef-

fects observed in option markets. Sch

obel and Zhu (1999) extended the Stein and

Stein’s formulation to a general case and derived an analytic solution for options.

Sch

obel and Zhu model consists of the following two correlated processes,

dS(t)

S(t)

= rdt + v(t)dW

(t),

dv(t)=

(

−v(t))dt +

(t), (3.28)

dt.

Differently from the Heston model, the modeling object is volatility v(t), not

variance. The volatility process is mean-reverting with a mean level of

and

a reverting speed parameter

. The parameter

is the volatility of volatility

and controls the variation of v(t). Therefore volatility speciﬁed to be a mean-

reverting Ornstein-Uhlenbeck process satisﬁes almost all desired requirements for

the stochastic volatility, which are well documented in empirical studies.

Additionally, conditional on v(s),v(t) is distributed according to Gaussian law,

namely,

v(t) ∼ N





(3.29)

with

= E[v(t)|v(s)] =

+(v(s) −

−

(t−s)

= Var[v(t)|v(s)] =

(1−e

−2

(t−s)

We observe that the conditional means of a mean-reverting square root process and a

mean-reverting Ornstein-Uhlenbeck process are identical. However, the conditional

variance m

is independent of the initial value v(s), and keeps constant over all time

interval [s,t] irrespective of how large the volatility v(s) is. Due to the Gaussian

property, the volatility v(t) can be negative. The probability for the volatility to be

negative is N(−m

√

). Using the parameter values that match to market data, we

ﬁnd that this probability is very small.

But even in the case that the negative volatil-

ity occurs, the asset process S(t) is still well-deﬁned. From the point of mathematical

The probability that v(T) becomes negative is given by P = N(−m

). For example, setting

= 4,

= 0.2,

= 0.1,T −t = 0.3andv

= 0.2givesP = 1.50×10

−9

. Setting

= 1,

= 0.2,

0.1,T −t = 0.5andv

= 0.2givesP = 1.87 ×10

−4

. These probabilities are so small that it does

not raise any serious problem at all in practical applications.

3.3 The Sch

obel-Zhu Model 57

view, a negative volatility leads to a reﬂected Brownian motion and a sign change

of the correlation term S(t)v(t)

dt. In this sense, negative volatility does not raise

any severe issue for option pricing. In practical applications, the mean-reverting

Ornstein-Uhlenbeck process can be easily and exactly simulated without any so-

phisticated techniques. A convenient simulation is a point that most researchers un-

derestimate and is very important for practitioners.

Now we compare this stochastic volatility model with Heston’s model. Looking

at the processes (3.28) and (3.4) again, we ﬁnd that the only difference between them

is the mean-reversion parameter

. While

in (3.28) generally differs from zero,

in (3.4) is zero. Since

gives a level that a volatility approaches in a long run,

process (3.4) does not seem to be very reasonable. Therefore, this restricted Heston

model can be considered as a special case of Sch

obel and Zhu model in terms of

equations (3.5) and (3.6). Sch

obel and Zhu model is reduced to the Heston model

by setting the following parameters:

= 0,

, (3.30)

where

and

stand for the parameters in process (3.4). However, note that

the parameters in process (3.5) are over-determined by (3.30), then for a wide range

of the values of

and

, the volatility process (3.4) can not be derived from

(3.5). This means that (3.4) and (3.5) are not mutually consistent in many cases.

Hence in this sense, the Heston model is not a special case of the Sch

obel and Zhu

model.

There are some confusing explanations about the above model setup in (3.28)in

literature. For example, Ball and Roma (1994) discussed the difference between the

absolute value process of v(t) and the reﬂected process of v(t), and claimed that the

above model setup in (3.28) implied the absolute value process since “the volatility

enters option pricing only as v

(t)” in Stein and Stein’s solution. Unfortunately, their

claim is incorrect. If we are working with an absolute value process, we can expect

the same option prices for

v(t)

= v(t). But we can not get the same option prices

for this case. Most rigorously, As shown in Sch

obel and Zhu (1999), for arbitrary

values of the long-term mean

= 0, the absolute value Ornstein-Uhlenbeck process,

the reﬂected Ornstein-Uhlenbeck process and the unrestricted Ornstein-Uhlenbeck

process are substantially different. Only for the special (symmetric) case

= 0the

reﬂecting barrier process coincides with the absolute value process. Furthermore,

we also can verify that the density function of the above Ornstein-Uhlenbeck pro-

cess process in (3.28) is identical to the one of the unrestricted Ornstein-Uhlenbeck

process and does not satisfy the boundary condition which is necessary for an abso-

lute value process.