Zhu J. Applications of Fourier Transform to Smile Modeling: Theory and Implementation
Подождите немного. Документ загружается.

16 1 Option Valuation and the Volatility Smile
As S
0
and r are given by markets, for each pair (K,T ) that are determined by an op-
tion contract, we can find a corresponding implied volatility. However, if we retrieve
the implied volatilities from a number of option prices with different strikes and
maturities, they often are not same. This phenomena called the volatility smile con-
tradicts the assumption in the Black-Scholes model that volatility is constant over
all strikes and maturities, and at the same time, indicates that the constant volatil-
ity in the Black-Scholes model should be too restrictive to capture the true market
movements. Implied volatility is then a “wrong” quantity generated by a “wrong”
pricing tool with a right market price.
Generally, volatility smile has two basic patterns: symmetric smile and skew.
Symmetric smile is referred to as the case where implied volatility increases if strike
moves away from the stock spot price. Down-sloping skew, also called sneer, cor-
responds the case of decreasing implied volatilities with increasing strikes. Corre-
spondingly, up-sloping skew stands for increasing implied volatilities with increas-
ing strikes. For a fixed strike, implied volatilities over different maturities may dis-
play a certain term structure which is called the volatility term structure. Expressing
all implied volatilities over strikes and maturities in a matrix form yields a smile
matrix or a smile surface.
1.3.2 Market Quotations
Due to the one-to-one correspondence between option price and its implied volatil-
ity, implied volatilities should content the same market information as the option
prices. However, option markets seem prefer to the implied volatilities for mar-
ket quotations. Compared with quoting directly with prices, quoting with implied
volatilities has the following advantages:
1. Quotations with implied volatilities clarify market situation and deliver a more
clear and transparent picture about market sentiments because implied volatility
standardizes option price in year, and is independent of the absolute values of
spot stock prices. Usually it is quoted in terms of strike (or moneyness K/S
0
)
and maturity.
2. Market participants can compare the relative expenses of different options easily
via implied volatility and can check the arbitrage conditions more conveniently.
3. Implied volatility allows us to gauge the historical movements of option prices
consistently and transparently, and also allows us to measure the deviation be-
tween the underlying and option markets by comparing implied volatility and
statistical volatility.
4. It is straightforward to estimate market volatilities for the options that are traded
less actively and less liquidly. Using some interpolation techniques and models
we can retrieve implied volatility for any strike and maturity based on smile
surface.
1.3 Volatility Quotations in Markets 17
However, oppositely to these advantages in valuing European-style options, im-
plied volatilities can not be applied to soundly value exotic derivatives involving
more than one strikes, for example, barrier options and clique options. Since im-
plied volatilities are generated by a “wrong” pricing machine, there is no natural
and reliable dynamics of the implied volatility. As a result, implied volatilities serve
only as market quotations for options, not as market observations for true volatili-
ties.
In stock option markets, a volatility surface is usually spanned by strike K (or
moneyness K/S
0
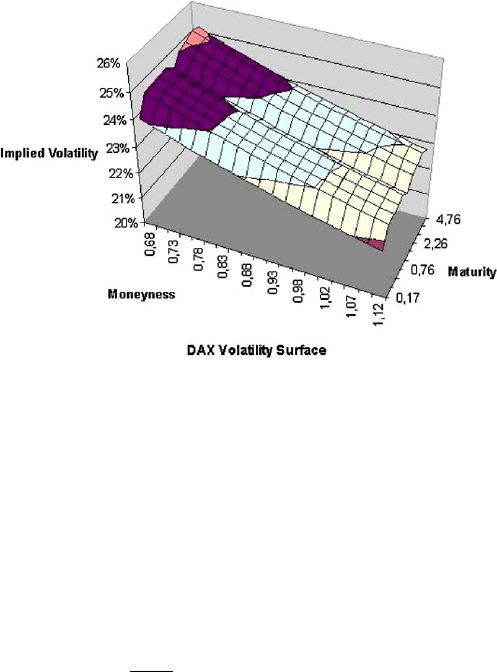
) and maturity T . In Figure (1.1), a volatility surface of DAX index
illustrates strong down-sloping smiles for all maturities with the higher out-of-the-
money (OTM) call volatilities and the lower in-the-money (ITM) call volatilities,
reflecting the clear market fear of a further decline of DAX prices during the finan-
cial crisis in 2009.
Fig. 1.1 The implied volatility surface of DAX index, as of March 12, 2009.
1.3.3 Special Case: FX Market
In FX option (foreign exchange option) markets, a volatility surface is given in terms
of Delta and maturity. This special quotation convention is popular for traders and
brokers, but not welcome for quants. We recall the risk-neutral FX process as fol-
lows:
dS(t)
S(t)
=(r −r
∗
)dt +
σ
dW(t), (1.34)

18 1 Option Valuation and the Volatility Smile
where r and r
∗
are the domestic and foreign interest rates respectively. Garman-
Kohlhagen (1983) derived a pricing formula for FX options within the Black-
Scholes framework, it reads
C
0
= S
0
e
−r
∗
T
N(d
1
) −Ke
−rT
N(d
2
), (1.35)
with
d
1
=
ln(S
0
/K)+(r −r
∗
+
1
2
σ
2
)T
σ
√
T
,
d
2
=
ln(S
0
/K)+(r −r
∗
−
1
2
σ
2
)T
σ
√
T
.
Delta is the first derivative of an option with respective to its underlying, and for FX
options it is equal to
Δ
= e
−r
∗
T
N(d
1
),
which again is a function of stock price, strike, maturity and volatility. Therefore
there is no clear functional relation between volatility and price if implied volatility
is given in terms of Delta. For example, if a quoted implied volatility at the point of
0.15 Delta (call) is equal to 0.12, we have
Δ
(
σ
= 0.12)=e
−r
∗
T
N(d
1
,
σ
= 0.12)=0.15.
FX option markets quote usually three most liquid options for a given maturity,
they are −0.15 Delta put, ATM call and 0.15 Delta call where ATM means that strike
K is equal to FX forward price, not spot price, namely K = S
0
e
(r−r
∗
)T
.LetK
1
,K
2
and K
3
correspond to the volatilities
σ
15P
,
σ
AT M
and
σ
15C
of the quoted options
respectively, we have the following relations,
−0.15 = −e
−r
∗
T
N
−
ln(S
0
/K
1
)+(r −r
∗
+
1
2
σ
2
15P
T)
σ
15P
√
T
, (1.36)
Δ
= −e
−r
∗
T
N
1
2
σ
AT M
√
T
≈ 0.5, K
2
= S
0
e
(r−r
∗
)T
, (1.37)
0.15 = e
−r
∗
T
N
ln(S
0
/K
3
)+(r −r
∗
+
1
2
σ
2
15C
T)
σ
15C
√
T
. (1.38)
Note that the Delta of short-maturity ATM option is approximately equal to 0.5.
Given (
σ
15P
,
σ
AT M
,
σ
15C
), we can numerically calculate (K
1
,K
2
,K
3
), and then estab-
lish a conventional volatility smile surface in terms of strike and maturity. However,
If the quoted Delta volatilities have changed, the corresponding strikes change too.
The translated FX volatility surface spanned by strike and maturity will be shifted
correspondingly. Meanwhile, some data sponsors and brokers such as Reuters pro-
vide a large range of Delta volatilities for puts with −0.10 Delta, −0.15 Delta,
−0.20 Delta, ···, −0.45 Delta, for calls with 0.45 Delta, 0.40 Delta, 0.35 Delta, ···,

1.3 Volatility Quotations in Markets 19
0.10 Delta. Given so many Delta volatilities, we can therefore establish a fine FX
volatility surface.
More interestingly, some data sponsors and brokers do not deliver directly Delta
volatilities, but the so-called butterfly volatility
σ
BF
, the so-called risk-reversal
volatility
σ
BF
and ATM volatility
σ
AT M
. The market conventions of the butterfly
volatility
σ
BF
and the risk-reversal volatility
σ
BF
are parallel to the trading strate-
gies named butterfly and risk-reversal, and given by
σ
RR
=
σ
15C
−
σ
15P
,
σ
BF
=
1
2
(
σ
15P
+
σ
15C
) −
σ
AT M
.
Therefore, we can express the Delta volatilities with
σ
BF
and
σ
RR
, and have
σ
15P
=
σ
AT M
+
σ
BF
−
1
2
σ
RR
, (1.39)
σ
15C
=
σ
AT M
+
σ
BF
+
1
2
σ
RR
. (1.40)
In this sense, the quotations with the butterfly volatility
σ
BF
and the risk-reversal
volatility
σ
BF
are equivalent to the quotation with two Delta volatilities. For more
details on FX option markets, please see Wystup (2006).

Chapter 2
Characteristic Functions in Option Pricing
We consider in this chapter a general It
ˆ
o process for stock prices. In a generalized
valuation framework for options, the distribution function of stock price is analyti-
cally unknown. To express (quasi-) closed-form exercise probabilities and valuation
formula, characteristic functions of the underlying stock returns (logarithms) are
proven to be not only a powerful and convenient tool to achieve analytical tractabil-
ity, but also a large accommodation for different stochastic processes and factors. In
first section, we derive two important characteristic functions under Delta measure
and forward measure respectively, under which two exercise probabilities can be
calculated. The pricing formula for European-style options may be expressed in a
form of inverse Fourier transform. As a result, we obtain a generalized principle for
valuing options under the risk-neutral measure via characteristic functions. There is
a corresponding extension for FX options.
Next in Section 2.2.1, we first demonstrate some nice properties of characteristic
function. As conditional expected value, characteristic function shares all proper-
ties of integration operator and expectation operator. The most important property
of characteristic function with respect to setting up a comprehensive option pricing
framework is that if stochastic factors are mutually independent, the characteris-
tic function of the sum of stochastic factors is just a product of the characteris-
tic function of each stochastic factor. In Section 2.2.2, we follow an approach of
Bakshi and Madan (2000) and interpret characteristic functions as Arrow-Debreu
prices in a Fourier-transformed space. As shown in Section 2.2.3 by some examples,
most popular pricing models, particularly, stochastic volatility models, admit ana-
lytical solutions for characteristic functions, and therefore, also analytical solutions
for valuation formulas in terms of inverse Fourier transform. The Black-Scholes
formula can be easily verified with the characteristic functions of normal distribu-
tion. Additionally, we can establish an equivalence between the Fourier transform
approach and the traditional PDE approach where the Feynman-Kac theorem and
Kolmogorov’s backward equation play a central role. Finally, as one of many advan-
tages of the Fourier transform approach, it allows us a modular valuation for options,
with which all relevant independent stochastic factors such as interest rates, volatil-
ities and jumps may be dealt with as a module in an unified valuation procedure.
J. Zhu, Applications of Fourier Transform to Smile Modeling, Springer Finance,
DOI 10.1007/978-3-642-01808-4
2,
c
Springer-Verlag Berlin Heidelberg 2000, 2010
21

22 2 Characteristic Functions in Option Pricing
The approach of the modular pricing will be discussed later in details throughout
this book, and provides us with large efficiency and rich flexibility in practical ap-
plications.
2.1 Constructing Characteristic Functions (CFs)
2.1.1 A General Process for Stock Price
We start with a rather general setting where the processes of two important financial
factors: stock price process (risky asset process) and risk-free short rate process.
Stock price S(t) is governed by the following It
ˆ
o process,
dS(t)
S(t)
= a(u(t),t)dt + b(v(t),t)dW
1
(t), (2.1)
where a(·,t) ∈ L : R
k
×[0,T] → R , b(·,t) ∈ L
2
: R
m
×[0,T] → R
n
and dW
1
is
a n-dimensional standard Brownian motion. L and L
2
denote the set of functions
y(t) such that
T
0
|
y(t)
|
dt < ∞ almost surely and
T
0
y
2
(t)dt < ∞ almost surely, re-
spectively. u(t) ∈ R
k
and v(t) ∈ R
m
could also follow It
ˆ
o processes and control the
process S(t). Defining x(t) ≡ lnS(t) and applying It
ˆ
o’s lemma yield
dx(t)=
a(u(t),t) −
1
2
b
2
(v(t),t)
dt +b(v(t),t)dW
1
(t). (2.2)
In fact, a(·,t) is irrelevant for the risk-neutral processes of dS(t) and dx(t).
For simplicity, we consider only a one-factor version of risk-free short rate pro-
cess r(t) which is defined by
dr(t)=c(r,t)dt + e(r,t)dW
2
(t), (2.3)
where c(·,t) ∈ L : R×[0,T ] → R, e(·,t) ∈ L
2
: R×[0,T ] → R and dW
2
is a one-
dimensional Brownian motion. All of the functions a,b,c and e satisfy the technical
conditions
1
that guarantee the existence of a solution of the above two SDEs. Under
the risk-neutral valuation, we have a simplified process for x(t),
1
The technical conditions sufficient for the existence of unique solution of stochastic differential
equation are the Lipschitz and the growth conditions. A function y(x,t) satisfies the Lipschitz
condition in x if there is a constant k such that for any x
1
and x
2
and any time t
y(x
1
,t) −y(x
2
,t) ≤k x
1
−x
2
.
Similarly, y(x,t) satisfies the growth condition in x if there is a constant k such that for any x
and any t
y(x,t)
2
≤ k(1+ x
2
).
2.1 Constructing Characteristic Functions (CFs) 23
dx(t)=
r(t) −
1
2
b
2
(v(t),t)
dt +b(v(t),t)dW
1
. (2.4)
In this general setting, the dynamics of the stock price S(t) are driven by a pure
diffusion W(t) as in the simple Black-Scholes model. The essential extensions here
are a stochastic interest rate r(t) and a stochastic volatility term b(·), that will be
specified in a more correct modeling. As documented in a number of empirical
studies, pure diffusive movements are not good enough to capture all statistical and
implied characteristics of asset prices. Different types of jumps may be a good com-
plement to the above setting, and will be discussed later.
To value FX options, we can adapt the process of x(t) by utilizing the interest
rate parity of FX rates, and obtain the following process for the FX rate x(t),
dx(t)=
r(t) −r
∗
(t) −
1
2
b
2
(v(t),t)
dt +b(v(t),t)dW
1
(2.5)
with r(t) and r
∗
(t) as the domestic and foreign interest rate respectively. The foreign
interest rate r
∗
(t) is governed by a similar process as r(t).
In the following, we use a simple functional form of b(v(t),t) for general discus-
sion, namely b(v(t),t)=v(t). A popular choice for b(·) may be b(v(t),t)=
V(t)
as in the Heston model (1993). Another more complicated and still tractable form
for b(·) may be the linear affine structure suggested by Dai and Singleton (2000).
2.1.2 Valuation of European-style Options via CFs
The general process for stock price given above includes the Black-Scholes world,
stochastic interest rates, stochastic volatilities, and can be extended by adding ran-
dom jumps. We know that the common property of the pricing formulas `alaBlack-
Scholes is the (log-) normal distribution of exercise probabilities. Obviously, in the
extended framework the exercise probabilities are no longer strictly (log-) normally
distributed. However, they can be expressed by the Fourier inversion of the associ-
ated CFs which may often have closed-form solutions with different specifications
of stochastic factors. Consequently, we can also express option pricing formula in a
(quasi) closed-form within this new framework.
In coherence with the existing financial literature, we assume that a European-
style option of the underlying stock S with strike price K can be valued by
C(S
0
,T;K)=E
Q
exp
−
T
0
r(t)dt
(S(T) −K) ·1
(S(T)>K)
= E
Q
exp
−
T
0
r(t)dt
S(T) ·1
(S(T)>K)
−E
Q
exp
−
T
0
r(t)dt
K ·1
(S(T)>K)
,
(2.6)
where Q denotes the risk-neutral (equivalent martingale) measure at the time T .Ac-
cording to Geman, El Karoui and Rochet (1995), Bj
¨
ork (1996) and others, in order

24 2 Characteristic Functions in Option Pricing
to simplify the calculations in the above equation, we can change the numeraire. For
the first term in the second equality, we choose the stock price S(t) as numeraire and
switch the measure Q to Q
1
, and for the second term we use the zero-coupon bond
to switch Q to the so-called T-forward measure Q
2
.
We first consider the change of the risk-neutral measure Q to the new measure Q
1
associated with numeraire S(t). According to the definition of equivalent measures
and the Girsanov theorem given in Section 1.2.4, we should construct a Radon-
Nikodym derivative using the corresponding numeraires,
dQ
1
dQ
(t)=
S(t)H(0)
H(t)S(0)
= exp
−
t
0
r(u)du
S(t)
S
0
= g
1
(t), (2.7)
where the numeraire underlying the risk-neutral measure is, as shown in Section
1.2.4, the money market account,
H(t)=exp
t
0
r(u)du
.
Obviously H(t) is equal to 1 at time 0, namely H(0)=1. It is easy to verify g
1
(t)
is a martingale with an expected value of one, and has the Del
´
eans exponential as
follows:
M(t)=exp
−
1
2
t
0
v(u)
2
du+
t
0
v(u)dW(u)
.
Applying Girsanov’s theorem yields
dW
∗
= dW −v(t)dt.
The risk-neutral process x(t) under the measure Q
1
is then changed to
dx(t)=
r −
1
2
v(t)
2
dt +v(t)dW(t)
=
r −
1
2
v(t)
2
dt +v(t)(dW
∗
(t)+v(t)dt)
=
r +
1
2
v(t)
2
dt +v(t)dW
∗
(t), (2.8)
where we can see that the drift term becomes r +
1
2
v(t)
2
under the new measure.
As shown in the Black-Scholes model, the risk sensitivity Delta, defined as the first
derivative of call price to spot price, namely
∂
C
∂
S
, could be interpreted as an exercise
probability under the measure Q
1
. In this sense, we label Q
1
as the Delta measure.
The second change of measures takes place between two numeraires: the money
market account H(t) and the zero-coupon bond B(t, T ). Given the process of the
risk-free short rate r(t), a zero-coupon bond maturing at time T is defined by
2.1 Constructing Characteristic Functions (CFs) 25
B(t, T )=E
exp(−
T
t
r(u)du)
.
The Radon-Nikodym derivative for a change of the risk-neutral measure Q toanew
measure Q
2
is given by
dQ
2
dQ
(t)=
B(t, T )H(0)
B(0,T)H(t)
= exp
−
t
0
r(u)du
B(t, T )
B(0,T)
= g
2
(t). (2.9)
It can be shown that g
2
(t) is a martingale with an expected value of one, and its
Dol
´
eans exponential is
M(t)=exp
−
1
2
t
0
σ
2
B
(u)du−
t
0
σ
B
(u)dW(u)
, (2.10)
where
σ
B
(u) is the volatility of B(t, T ). Dependently on the specification of the
short-rate process, one can derive a pricing formula for B(t, T ). Since any risky asset
under the measure Q
2
takes the zero-coupon bond B(t, T ) as numeraire, therefore
an asset under the measure Q
2
can be regarded as the forward price of this asset for
time T under the measure Q. In this sense, the measure Q
2
is called a forward T −
measure, or for short, forward measure. At time T , the Radon-Nikodym derivative
g
2
(t) has a special simplified form
g
2
(T)=
exp(−
T
0
r(u)du)
B(0,T)
=
1
H(T )B(0,T )
. (2.11)
As a property of Radon-Nikodym derivative, g
j
(t), j = 1,2, define two density
functions at t. We can also call {g
1
(t)}
t0
the unit discounted stock process and
{g
2
(t)}
t0
the unit discounted bond process due to their martingale property.
2
Under
these new measures, the option pricing representation (2.6) can be restated as
C
0
= S
0
E
Q
1
1
(x(T)>lnK)
−B(0,T)KE
Q
2
1
(x(T)>lnK)
(2.12)
= S
0
F
Q
1
1
(x(T) > lnK) −B(0,T )KF
Q
2
2
(x(T) > lnK).
This representation for an option pricing formula is similar to the Black-Scholes
formula where the probabilities F
Q
j
, j = 1,2, in the latter case are two standard
normal distributions. Now we express these probabilities by the Fourier transform.
The characteristic functions of F
Q
j
j
are defined by
f
j
(
φ
) ≡ E
Q
j
[exp(i
φ
x(T))] for j = 1, 2. (2.13)
2
These two processes are also termed as likelihood processes because they imply two probabilities.

26 2 Characteristic Functions in Option Pricing
By using the above two Radon-Nikodym derivatives again, we obtain new expres-
sions for the CFs f
j
(
φ
), j = 1,2, under the original risk-neutral measure Q:
f
1
(
φ
) ≡ E
Q
1
[exp(i
φ
x(T))] = E
Q
[g
1
(T)exp(i
φ
x(T))] (2.14)
and
f
2
(
φ
) ≡ E
Q
2
[exp(i
φ
x(T))] = E
Q
[g
2
(T) exp(i
φ
x(T))] . (2.15)
Given the CFs f
j
(
φ
) of x(T) under the two different measures Q
j
, the density
function y
j
(x(T)) of x(T ) is simply the inverse Fourier transform,
y
j
(x(T)) =
1
2
π
R
f
j
(
φ
)e
−i
φ
x(T)
d
φ
, j = 1,2. (2.16)
Using the density function y
j
(x(T)) and denoting a = lnK, we can calculate the
exercise probability F
j
as follows:
F
j
(x(T) > a)=
∞
a
y
j
(x)dx
=
∞
a
1
2
π
R
f
j
(
φ
)e
−i
φ
x
d
φ
dx
=
1
2
π
R
f
j
(
φ
)
∞
a
e
−i
φ
x
dx
d
φ
,
where we have changed the order of two integrations by applying the Fubini theo-
rem. A further straightforward calculation yields
F
j
=
1
2
+
1
2
π
R
f
j
(
φ
)
e
−i
φ
a
i
φ
d
φ
. (2.17)
Note that the probability F
j
must be real, the above expression can be rewritten as
(see Stuart and Ord, 1994),
F
j
=
1
2
+
1
π
∞
0
Im( f
j
)cos(
φ
a) −Re( f
j
)sin(
φ
a)
φ
d
φ
,
=
1
2
+
1
π
∞
0
Re
f
j
(
φ
)
exp(−i
φ
lnK)
i
φ
d
φ
, j = 1,2, (2.18)
where Im and Re denote the imaginary and real part of complex number respec-
tively. The last expression of F
j
allows us to carry out the integration over the half
real line, instead of over the whole real domain.
This new expression for the probabilities F
j
has some advantages: Firstly, we can
show later that in the most existing and new option pricing models the CF f
j
(
φ
) can
be expressed by elementary functions, and have analytical solutions. Secondly, F
j
contains only a single integral which can be calculated in an efficient way. Finally,
these expressions are independent of the specifications of the processes of individual
stochastic factors. Therefore, the above pricing approach offers us a comprehensive
