Zhu J. Applications of Fourier Transform to Smile Modeling: Theory and Implementation

Подождите немного. Документ загружается.

282 11 Libor Market Model with Stochastic Volatilities

A simple and useful parametrization for a time-homogeneous volatility term struc-

ture is the following

(t)=v

(t, a, b, c, d) :=[a(T

−t)+b]e

−c(T

−t)

+ d. (11.16)

With this formulation, the caplet volatility ˆv

maybeexpressedby

ˆv





[a(T

−t)+b]e

−c(T

−t)

+ d



dt.

As ˆv

,0 < j < M + 1, have been retrieved from the market data, the parameters

{a,b,c,d} may be calibrated to ﬁt the caplet volatilities. A favorite feature of this

ABCD parametrization is its ability to capture the different forms of the volatil-

ity term structure. For example, the ATM caplet volatility curve in Figure (11.1)

displays an inverse humped form with higher short-term and long-term volatilities

and lower medium-term volatilities, due to the credit crunch since 2007.

Brigo and

Mercurio (2006) provided an excellent discussion how to describe v

(t) with various

parametric formulations.

Applying the retrieved forward or instantaneous volatilities to the processes in

(11.11), we are able to simulate LMM in a simple manner. The simulation of LMM

is a multi-factor simulation that we have brieﬂy examined in Chapter 5 in the con-

text of a multi-asset model for assets. The key for such simulation is to generate

correlated Gaussian random variables, perhaps with the help of the Cholesky de-

composition. For more advanced topics on the simulation of LMM, the readers are

referred to Glasserman (2004).

11.3 Swap Market Model

11.3.1 Model Setup

Interest rate swaps are very liquid instruments and allow two trade participants to

exchange ﬁxed cash-ﬂows against ﬂoating cash-ﬂows. A swaption allows its holder

to enter a pre-determined swap in its maturity. Therefore, besides strike and option

maturity, the length of underlying swap is also an important parameter for swaption

contract. The payoff of a payer (receiver) swap is given by

SW (t;n,m)=

m−1

∑

j=n

(t) −K]B(t,T

j+1

)

where

= 1 for payer swap and

= −1 for receiver swap. In a reset date when a

swap contract is signed, the strike K is chosen to set the present value of the swap

In usual cases, caplet volatility curves are hump-shaped as a camel’s back with with lower short-

term and long-term volatilities and higher medium-term volatilities.

11.3 Swap Market Model 283

Fig. 11.1 The market ﬂat volatility surface of caps, as of as of February 11, 2009.

Fig. 11.2 The retrieved implied volatility surface of caplets, as of February 11, 2009.

284 11 Libor Market Model with Stochastic Volatilities

equal to zero. Such a strike making the value of a swap equal to zero is referred to

as swap rate, and may be easily expressed as

n,m

(t)=

∑

m−1

j=n

(t)B(t,T

j+1

)

∑

m−1

j=n

B(t, T

j+1

)

B(t, T

) −B(t,T

)

A(t;n, m)

, (11.17)

with

A(t;n, m)=

m−1

∑

j=n

B(t, T

j+1

that is termed as swap annuity or as the present value of a basis point (PVBP), and

may be interpreted as a weighted sum of (m −n −1) discount factors during the

swap period. Correspondingly, a payer (receiver) swaption has the following payoff

SW T (t;n, m)=max[SW (t;n,m),0]

= max



m−1

∑

j=n

(t) −K]B(t,T

j+1

),0



= max



A(t;n, m)[S

n,m

(t) −K], 0



. (11.18)

In the light of the above equation, swaption may be considered as an option with

swap rate S

n,m

(t) as the underlying, and swap annuity as an effective discount factor.

In fact, Swap Market Model (SMM) is based on swap measure with swap annuity

as numeraire, and the corresponding Radon-Nikodym derivative between the risk-

neutral measure and the swap measure is given by

(t)=

H(t)A(0;n,m)

H(0)A(t;n,m)

H(t)A(0;n,m)

A(t;n, m)

. (11.19)

Furthermore, we assume that the swap rate S

n,m

(t) under the swap measure follows

a driftless geometric Brownian motion,

n,m

(t)

n,m

(t)

= v

dW(t). (11.20)

A straightforward application of the above numeraire change leads to a Black76-

like pricing formula for payer swaption,

SW P(0;n,m)=E



H(T

)

max



A(T

;n,m)[S

n,m

) −K], 0





= A(0;n, m)E



max[S

n,m

) −K, 0]



= A(0;n, m)



n,m

(0)N(d

) −KN(d

)] (11.21)

with

11.3 Swap Market Model 285

ln(S

n,m

(0)/K)+

√

ln(S

n,m

(0)/K) −

√

This is the broadly applied pricing formula for plain-vanilla swaptions in market,

the corresponding implied volatilities are used as market quotations.

There are some important implications of SMM, which may help us better un-

derstand the essence of SMM and its relationship to LMM.

1. Firstly, swap measure Q

associated with the particular numeraire A(t;n,m) de-

pends on n and m, this means that each swap measure is so particular that a SMM

is only valid for a single swap rate. It is immensely tedious and involved to unify

all swap rates in an unique swap measure.

2. Secondly, it is relatively easy to build up an uniﬁed market model for swap rates

with a same tenor (see Musiela and Rutkowski (2006), Zhu (2007b)). Since Libor

can be regarded as a swap rate with the tenor of one period, such a generalized

SMM embraces LMM as a special case.

3. Next, swaptions can be classiﬁed into three subgroups according to n and m.

As mentioned above, one group is the swaptions with constant tenor, it means

that (m −n) is equal to a constant, this group is called co-sliding swaptions or

constant-tenor swaptions. Most CMS (Constant Maturity Swap) products use

constant-tenor swap rates as underlying index. The second group includes all

swaptions with the same terminal date T

, and is called co-terminal swaptions.

For examples, the underlyings of a Bermudan swaption are co-terminal swap

rates. The so-called co-initial swaptions is a set of swaptions with the same start

date T

. A few interest rate products use co-initial swap rates as the underly-

ing.

4. Finally, swap rate S

n,m

(t) is a function of (m −n) Libors, and therefore, depen-

dent on the correlations between these Libors. In this sense, swaptions are also

the correlation products of Libors, and the market quotations of swaptions pro-

vide us with the information on the correlation structure of Libors. As a result,

swaption variance may be approximated by the covariance of the weighted log

returns of successive Libors (see Brigo and Mercurio (2006)).

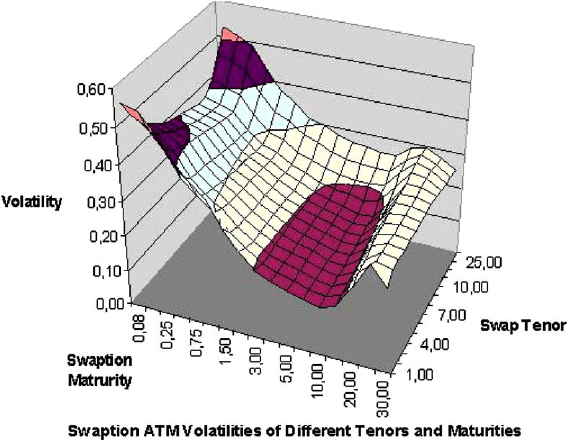
Since swaps could last from one year to 30 years, the market quotations for swap-

tions have one dimension more than for caps, namely the length of underlying swap,

or sometimes called the tenor of swap. Figure (11.3) shows the market ATM swap-

tion volatilities as of February 11, 2009, that also shapes a surface of two dimen-

sions of option maturity and swap tenor. For a certain swap tenor, we can draw an

ATM swaption volatility curve from an ATM swaption surface. As shown in Fig-

ure (11.3), such a swaption volatility curve, as its caplet counterpart, is inversely

humped in February, 2009.

286 11 Libor Market Model with Stochastic Volatilities

Fig. 11.3 Market ATM swaption volatilities, as of February 11, 2009.

11.3.2 Correlation Structure

We now brieﬂy examine how to value a swaption in a standard Libor Market Model,

and by this way, we may better expound how the correlation structure of Libors af-

fects the pricing of swaptions. As seen in the pricing formula for caplet/ﬂoorlet in

LMM, the values of caps and ﬂoors are independent of the correlation coefﬁcients

,0 < i, j < M+1. Therefore, caps and ﬂoors are insensitive to correlations, and do

not provide any information on correlations. However, many interest rate derivatives

are sensitive to the correlations between Libors, and the simulation of LMM requires

a well-deﬁned correlation matrix. On the other hand, we know that swaptions imply

such information. As the number of the correlation coefﬁcients is M(M −1)/2, a

parametrization of the correlation matrix is necessary, in order to make an efﬁcient

retrieving of correlations from swaptions feasible. Before we propose a parameter-

ized correlation matrix, we may observe the following stylized facts:

1. Two closely neighbored Libors are more highly correlated than two distanced

Libors. This implies that a change of an interest rate in a yield curve causes more

changes in its near segment than in distanced segments.

2. The correlation of two Libors should be positive. As a result, a positive shift of

an interest rate might leads to positive shifts of other interest rates.

To formulate these facts quantitatively, denote

as the matrix of instantaneous

correlations,

11.3 Swap Market Model 287

⎛

⎜

⎝

···

1 ···

··· ··· 1 ···

··· 1

⎞

⎟

⎠

= W

. (11.22)

The ﬁrst parameterization of

is simple and based on a single parameter q,

= e

−q|T

−T

, q > 0. (11.23)

The resulting correlations

satisfy the above stylized facts. Additionally, for a

suitable q, the correlation matrix

may be positive semi-deﬁnite, and makes sense.

The formulation (11.23) is then a simple and still reasonable parameterization.

A small extension of the formulation (11.23) may be the following,

+(1 −

−q|T

−T

. (11.24)

Obviously, when T

is far away from T

, their correlation

approaches to

asymp-

totically, whereas

in the formulation (11.23) goes to zero. Therefore, the param-

eter

is interpreted as the asymptotical instantaneous correlation. Rebonato (1999)

proposed a similar formulation with three parameters,

+(1 −

−|i−j|(p−q(max(i, j)−1))

. (11.25)

However, the correlation matrix of this parameterization is often not positive semi-

deﬁnite. Additional repair of the correlation matrix

via correcting eigenvalues of

is then necessary.

Schoenmakers and Coffey (2000) suggested several full rank formulations for the

correlation matrix. The favorite features of the resulting matrix are always positive

semi-deﬁnite, and parsimonious in parameters. The following two formulations are

of particular interest in practical applications.

1. Robust full-rank formulation:

= exp



−

|i − j|

M −1



−ln

+ q

M −1 −i− j

M −2





. (11.26)

2. Improved robust full-rank formulation:

= exp



−

|i − j|

M −1

(−ln

+ q

+ j

+ ij−3Mi+ 3Mj+ 3i + 3 j +2M

−M −4

(M −2)(M −3)



(11.27)

It should be emphasized that the correlation matrix

describes the correlations

of the Brownian motions in Libor process L

(t), not the correlations between Libors

themselves. The correlations of Libors involve not only Libors themselves, but also

288 11 Libor Market Model with Stochastic Volatilities

their volatilities. As shown in Brigo-Mercurio (2006) and Rebonato (1999), such

Libor correlation could be approximated by

),L

)) ≈



(t)v

(t)dt





(t)dt





(t)dt

, k  min(i, j), (11.28)

that is also called terminal correlation in ﬁnancial literature. It is easy to observe that

even if

is equal to 1,

),L

)) may not be 1. Additionally, the volatilities

of L

(t) and L

(t) have a signiﬁcant effect on

),L

)). An extreme example

may be the case where two volatility functions v

(t) and v

(t) are nearly orthogonal

and makes the terminal correlation near to zero. Therefore, the parametrization of

volatility functions has an immediate and direct impact on the values of terminal

correlations.

Now we recall the deﬁnition of swap rate S

n,m

(t) in (11.17) and rewrite it as

follows

n,m

(t)=

∑

m−1

j=n

(t)B(t,T

j+1

)

∑

m−1

j=n

B(t, T

j+1

)

m−1

∑

j=n

(t)L

(t) (11.29)

with

(t)=

B(t, T

j+1

)

A(t;n, m)

Obviously,

(t) itself is stochastic. In order to express swap rate as a linear combi-

nation of Libors, we perform the following approximation

n,m

(t) ≈

m−1

∑

j=n

(0)L

(t),

with the weights frozen at the origin,

(0)=

B(0,T

j+1

)

A(0;n,m)

Note that

(t) itself depends on zero-coupon bond and therefore also on L(t),Hull

and White (1999), Andersen and Andreasen (2000) give the more sophisticated for-

mulations of the weights

(t) by deriving the complete dynamics of S

n,m

(t) depen-

dently on L(t).

Without the detailed derivation of these two formulations for

(t),

we just give them for reference:

Many numerical examples conducted by author have shown that the difference between all three

versions of w

(t) is negligible in most cases.

11.3 Swap Market Model 289

Hull and White (1999):

(t)=

(t)+

m−1

∑

i=n

(t)

∂ω

(t)

∂

(t)

. (11.30)

Andersen and Andreasen (2000):

(t)=

∂

n,m

(t)L

(t)

∂

(t)S

n,m

(t)

. (11.31)

It is clear that the swaption annuity A(t;n,m) is a weighted sum of different

zero-coupon bonds B(t,T

j+1

), which are used as numeraire for forward measure

in LMM. By intuition, a swap measure should be also a weighted sum of differ-

ent forward measures Q

j+1

. This indicates that the process of a swap rate can be

appropriately approximated by a weighted sum of different Libor processes under

their own measures Q

j+1

and does not involve some speciﬁc forward measures. As

a consequence, if we approximate the swaption volatility v

by caplet volatilities,

is uniquely determined by the volatilities v

(t) of Libors L

(t) and their correla-

tions, and is independent of the drift adjustments

(t). This feature distinguishes

the pricing of a swaption from the pricing of a CMS derivatives. This subtle dif-

ference between swap rate and CMS rate leads to the different expression of their

stochastic processes, and will be discussed later in more details. Consequently we

have the following process for S

n,m

(t),

n,m

(t) ≈

m−1

∑

j=n

(0)dL

(t)

m−1

∑

j=n

(0)L

(t)v

(t)dW

The next step is re-formulate dS

n,m

(t) in a log-normal process as follows:

n,m

(t)

n,m

(t)

= S

n,m

(0)

−1

m−1

∑

j=n

(0)L

(0)v

(t)dW

= v

(t)dW

(t), (11.32)

where the volatility of swap rate takes the following form

(t)=

m−1

∑

i=n

m−1

∑

j=n

(0)

(0)L

(0)

n,m

(0)

(t)v

(t). (11.33)

The approximated swap rate process in (11.32) has no drift and coincides with the

one in SMM.

By freezing the dynamics S

n,m

(t) partially to S

n,m

(0), we can clearly see the

effects of the correlation coefﬁcient

on the volatility of a swap rate, and at the

290 11 Libor Market Model with Stochastic Volatilities

same time, can conclude that the forward measure Q

does not change the volatility

(t). The formula (11.33) is referred to as the Rebonato formula, and establishes

a close relationship between Libors and swaptions within LMM. Given the term

structure of Libor volatility v

(t) and swaption volatilities v

for different tenor and

maturity pair (n,m), we are able to estimate the correlation parameters in the above

various correlation formulations by considering the following optimization:

= argmin

∑

(

) −(v

Market

)

|, (11.34)

where

denotes the set of the parameters for correlation matrix. v

(

) and v

Market

are the theoretical and market swaption volatilities respectively.

Another immediate application of the Rebonato formula is to bootstrap the

volatility v

(t) of Libor dynamics given an endogenous correlation matrix. To this

end, we assume that v

(t) is piecewise constant, the Rebonato formula may be

rewritten in the following discrete form,

m−1

∑

i=n

m−1

∑

j=n

(0)

(0)L

(0)

n,m

(0)

n−1

∑

h=0

)

. (11.35)

Based on this formulation, we have a forward bootstrapping procedure to retrieve

the volatility v

(t), 0 < j < M + 1:

• Step 1: For the ﬁrst Libor L

, v

) is just the caplet volatility of L

. No further

calculation is required.

• Step 2: This step includes two small steps.

1. Step 2a: The volatility v

;1,2) of swap rate S(t;1,2) has to do with v

)

and v

) only. Given v

;1,2) and v

), we can simply compute v

)

by applying the formula (11.35).

2. Step 2b: For the caplet volatility ˆv

, we recall the following relationship

ˆv

(

)=v

)

+ v

)

which allows us to obtain v

) immediately. This step in fact ﬁts the caplet

volatility of a Libor.

• Step 3: This step includes three small steps.

1. Step 3a: After v

),1  i  M −1,1  j  M −2, are derived, we attempt to

solve v

). To this end, we use the volatility v

;1,n) of S(t;1, M).Itis

easy to see now that v

) is the only variable that is unknown in Rebonato’s

formula (11.35). The ﬁnal equation for v

) is a quadratic equation. To

ensure the solution to be positive, it is reasonable to take the bigger one of

two solutions.

2. Step 3b: We repeat step 3a and use the volatility v

; j,M), 0 < j < M −1,

of swap rates S(t; j, M) to obtain v

11.3 Swap Market Model 291

3. Step 3c: Similar to Step 2b. We compute v

M−1

) of L

via the caplet

volatility ˆv

By denoting v

j−1

) as v

, the above bootstrapping procedure delivers a time-

inhomogeneous volatility term structure for each Libor, which can be illustrated by

the following matrix:

] (T

] ······ (T

M+1

]

(t) v

No ······ No

(t) v

······ No

······

(t) v

······ v

M,M

The bootstrapping method is also called the cascade calibration, and performs a

self-calibration to caps and swaption markets. Its advantages lie in the good ﬁtting

of LMM to the ATM swaption volatilities and the easy implementation without the

application of extensive optimization methods. But the drawbacks of the cascade

calibration are also obvious. Firstly, there is often no real solution in Step 3a and

3b. Secondly, the retrieved volatilities often oscillate strongly. As a result, the term

structure of volatility is not smooth, and by nature, is not time-homogeneous.

11.3.3 Convexity Adjustments for CMS

Many interest derivatives use the constant-tenor swap rate S

n,m

) for a constant

c = m −n as the underlying index, and pay it at another time T

k+1

. Generally, a

swap rate discounted with a zero-coupon bond instead of a swap annuity is called a

constant maturity swap (CMS) rate. In other words, a CMS rate is a swap rate under

a forward measure. Applying It

o’s lemma, we can derive the process of S

n,m

(t)

under an arbitrary forward measure Q

k+1

n,m

(t) ≈

m−1

∑

j=n

(0)dL

(t)

≈

m−1

∑

j=n

(0)L

(t)

dt +

m−1

∑

j=n

(0)L

(t)

(t)dW

≈ S

n,m

(t)[

(0)dt +v

(0)dW

with

(0)=S

n,m

(0)

−1

m−1

∑

j=n

(0)L

(0)

To avoid notational confusion, we denote y(t) as CMS rate in this subsection, the

process of CMS rate then reads