Зенкевич Н.А. Практикум по исследованию операций
Подождите немного. Документ загружается.

3.1. ЗАДАЧА О МАКСИМАЛЬНОМ ПОТОКЕ 81
Строим множество S
2
= {s, 2, s
′
}, s
′
∈ S
2
. Выбираем путь P
2
(x, y), ненасыщенный
относительно потока f
2
: P
2
(x, y) = {(s, 2), (2, s
′
)}. Величина Θ
2
= min{2, 1} = 2. Пере-
считываем матрицу в соответствии алгоритмом, получаем матрицу C
3
:
s 1 2 3 4 5 6 s’
s 0 1 4
1 2 0 1 2
2 7 0 0
3 2 4 0
4 1 3 1
5 4 3 1
6 2 6 1 3
s’ 2 1 9
Строим множество S
3
= {s, 5, s
′
}, s
′
∈ S
3
. Выбираем путь P
3
(x, y), ненасыщенный
относительно потока f
3
. P
3
(x, y) = {(s, 5), (5, s
′
)}. Величина Θ
3
= min{4, 1} = 1. Пере-
считываем матрицу в соответствии алгоритмом, получаем матрицу C
4
:
s 1 2 3 4 5 6 s’
s 0 1 5
1 2 0 1 2
2 7 0 0
3 2 4 0
4 1 3 1
5 5 3 0
6 2 6 1 3
s’ 2 1 9
Строим множество S
4
= {s, 5, 4, 6, s
′
}, s
′
∈ S
4
. Выбираем путь P
4
(x, y), ненасы-
щенный относительно потока f
4
: P
4
(x, y) = {(s, 5), (5, 4), (4, 6), (6, s
′
)}. Величина Θ
4
=
min{3, 3, 1, 3} = 1. Пересчитываем матрицу в соответствии алгоритмом, получаем мат-
рицу C
5
:

82 Глава 3. СЕТИ
s 1 2 3 4 5 6 s’
s 0 1 2
−
1 2 0 1 2
2 7 0 0
3 2 4 0
4 1 4
+
0
5 6 2 0
6 2 6 1 2
s’ 2 1 10
Строим множество S
5
= {s, 5, 4, 1, 6, s
′
}, s
′
∈ S
5
. Выбираем путь P
5
(x, y), ненасы-
щенный относительно потока f
5
. P
5
(x, y) = {(s, 5), (5, 4), (4, 1), (1, 6), (6, s
′
)}. Величина
Θ
5
= min{2, 2, 1, 2, 2} = 1. Пересчитываем матрицу в соответствии алгоритмом, получа-
ем матрицу C
6
:
s 1 2 3 4 5 6 s’
s 0 1 1
1 2 0 2 1
2 7 0 0
3 2 4 0
4 0 5 0
5 7 1 0
6 3 6 2 1
s’ 2 2 11
Строим множество S
6
= {s, 2, 5, 4}, s
′
/∈ S
6
, следовательно мы не можем построить
путь P
6
(x, y), ненасыщенный относительно потока f
6
. Поток f
6
– максимальный.
Величину максимального потока можно найти по формуле f
6
= C
0
− C
6
:
3.2. ЗАДАЧА МИНИМИЗАЦИИ СЕТИ 83
s 1 2 3 4 5 6 s’
s 1 3 3
1 -1 1 −1 1
2 −3 2 1
3 -1 -2 3
4 1 −2 1
5 −3 2 1
6 −1 -3 −1 5
s’ −1 −1 −5
Просуммировав значения элементов первой строки матрицы потока f
6
или последнего
столбца, получим мощность максимального потока f
max
= 1 + 3 + 3 = 1 + 1 + 5 = 7.
Строим минимальное сечение (S, S
′
). Для этого находим множество S = {1, 2, 4, 5},
тогда S
′
= N \ S = {3, 6}. По сети находим пропускные способности ребер, соединяющих
узлы из множеств S и S
′
и считаем пропускную способность сечения u(S, S
′
).
u(S, S
′
) = u(1, 3) + u(2, 3) + u(1, 6) + u(4, 6) + u(5, S
′
) + u(2, S
′
) = 1 + 2 + 2 + 1 + 1 = 7,
что подтверждает справедливость теоремы о максимальном потоке.
3.2 Задача минимизации сети
Задача минимизации сети состоит в нахождении ребер, соединяющих все узлы сети и
имеющих минимальную суммарную длину. Очевидно, что решение задачи не должно
содержать циклов.
Отсутствие циклов в минимальной сети привело к ее названию – минимальное дерево-
остов. В любой сети минимальное дерево-остов можно определить следующим итера-
тивным процессом. Начать с любого узла и соединить его с ближайшим узлом сети.
Соединенные два узла образуют связное множество, а остальные узлы – несвязное
множество. Далее в несвязном множестве выбрать узел, который расположен ближе
других (на кратчайшем расстоянии) к любому из узлов связного множества. Скоррек-
тировать соответствующим образом связное и несвязное множества и повторять процесс
до тех пор, пока в связное множество не попадут все узлы сети. В случае одинаково уда-
ленных узлов выбирать любой из них, что указывает на неоднозначность минимального
дерева-остова.
84 Глава 3. СЕТИ
Пример 3.2.1.
Интернет провайдер
”
NetTel“ планирует создание оптоволоконной сети (рис. 3.2.1)
для обслуживания семи районов-новостроек. Числа на ребрах указывают длину опто-
волоконного кабеля, соединяющего соответствующие узлы. Узел S представляет точ-
ку подключения к сети интернет, а остальные узлы (1-7) соответствуют семи районам.
Отсутствие ребра между двумя узлами означает, что соединение соответствующих но-
востроек либо связано со слишком большими затратами, либо физически невозможно.
Нужно найти такие ребра, которые потребуют кабель минимальной длины для связи
(прямой или через другие пункты) всех районов с точкой подключения к сети интернет.
1
S
2
3
7
7
4
5
4
2
4
5
2
8
6
6
7
3
1
6
3
Рис 3.2.1. Оптоволоконная сеть для обслуживания семи районов-новостроек
Начальный этап итерационного процесса решения этой задачи представлен на рис.
3.2.2. При любом выборе начального узла получается одно и то же оптимальное ре-
шение. В данном примере логично начинать вычисления с узла S, т. е. в начальный
момент он соответствует множеству "связных узлов". Множество "несвязных узлов"
представлено узлами 1, 2, 3, 4, 5, 6, 7. Формально это можно записать как T = {S},
T = {1, 2, 3, 4, 5, 6, 7}.
1
S
2
3
7
7
4
5
4
2
4
5
2
8
6
6
7
1
6
3
3
Рис 3.2.2. Итерационный процесс построения минимальной сети
3.2. ЗАДАЧА МИНИМИЗАЦИИ СЕТИ 85
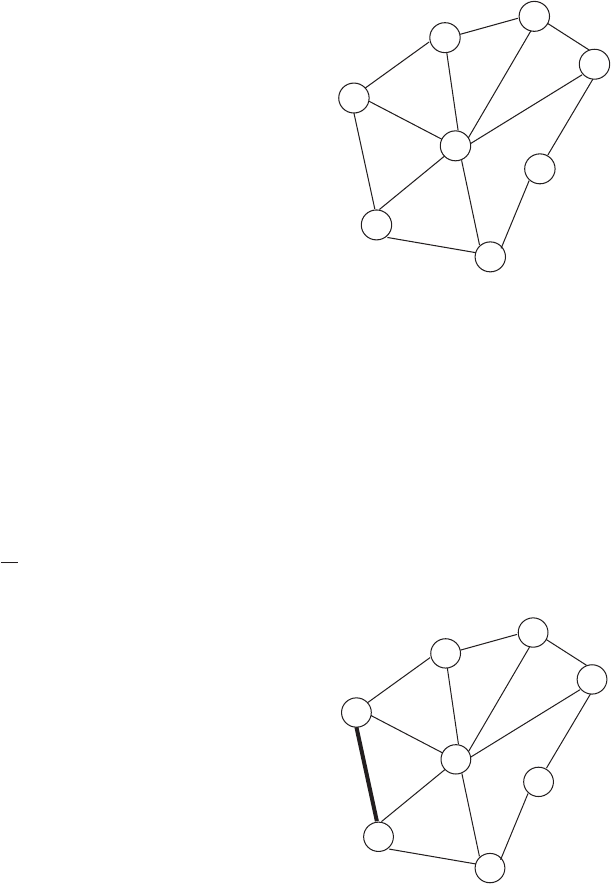
Итерация 1. Узел S соединить с узлом 2, ближайшим к S в множестве
T = {1, 2, 3, 4, 5, 6, 7}. Результаты итерации 1 на рис. 3.2.2 показывают, что T = {S, 2},
T = {1, 3, 4, 5, 6, 7}.
Итерация 2. Узлы S и 2 (из множества T ) связаны. На итерации 2 выбрать узел в
T = {1, 3, 4, 5, 6, 7}, ближайший к одному из узлов в T = {S, 2}, Поскольку кратчайшим
оказывается расстояние 2 между узлами 2 и 4 (см. итерацию 1 на рис. 3.2.2), получим
T = {S, 2, 4}, T = {1, 3, 5, 6, 7}.
6
1
S
2
3
7
7
4
5
4
2
4
5
2
8
6
7
1
6
3
3
6
Рис 3.2.3. Итерационный процесс построения минимальной сети
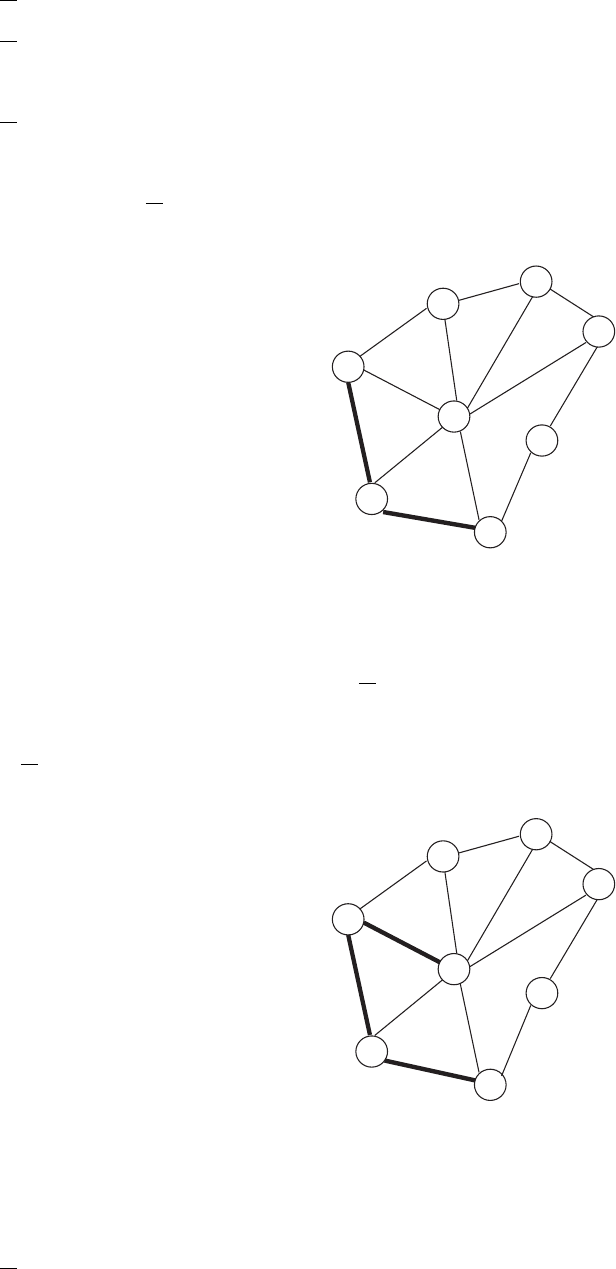
Итерация 3. На итерации 2 (рис. 3.2.3) выбираем кратчайшее расстояние от узлов
из T = {S, 2, 3} до всех узлов из T = {1, 4, 5, 6, 7}. Таким образом, можем связать узлы
S и 3, таким обрезом получаем на итерации 3 новые связные множества T = {S, 2, 4, 3}
и T = {1, 5, 6, 7}.
2
1
S
2
3
7
7
4
5
4
4
5
2
8
6
7
1
6
3
3
6
Рис 3.2.4. Итерационный процесс построения минимальной сети
Итерация 4. Результаты, полученные на итерации 3 см. рис. 3.2.4 показывают, что
следует связать узлы 3 и 5, т. е. новые связные множества имеют вид T = {S, 2, 3, 4, 5},
T = {1, 6, 7}.
86 Глава 3. СЕТИ
6
1
S
2
3
7
7
4
5
4
2
4
5
2
8
6
7
1
6
3
3
6
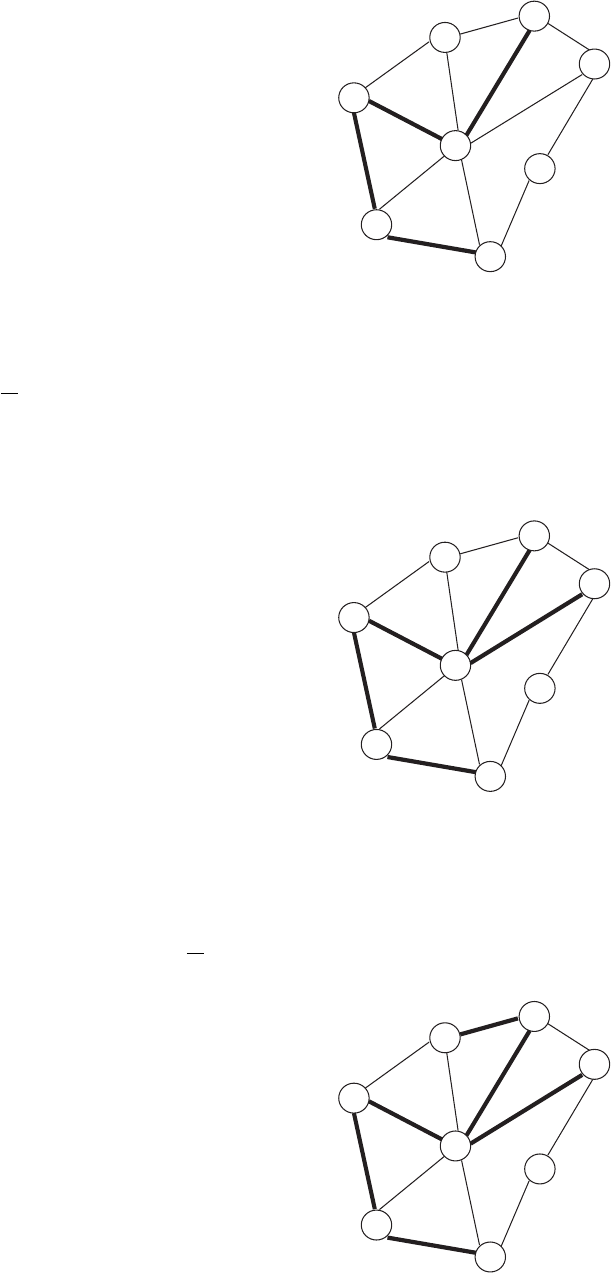
Рис 3.2.5. Итерационный процесс построения минимальной сети
Итерация 5. На итерации 4 были получены связные множества T = {S, 2, 3, 4, 5},
T = {1, 6, 7}. Оценивая расстояния между узлами, входящими в эти множества, получим,
что следует связать узлы 3 и 6. На итерации 5 получаем T = {S, 2, 3, 4, 5, 6} и T = {1, 7}.
Переходим к итерации 6.
6
1
S
2
3
7
7
4
5
4
2
4
5
2
8
6
7
1
6
3
3
6
Рис 3.2.6. Итерационный процесс построения минимальной сети
Итерация 6. Результаты итерации 5, представленные на рис. 3.2.6 показывают, что
следует связать узлы 5 и 1, на итерации 6 получаем новые связные множества: T =
{S, 2, 3, 4, 5, 6, 1},
T = {7}.
6
1
S
2
3
7
7
4
5
4
2
4
5
2
8
6
7
1
6
3
3
6
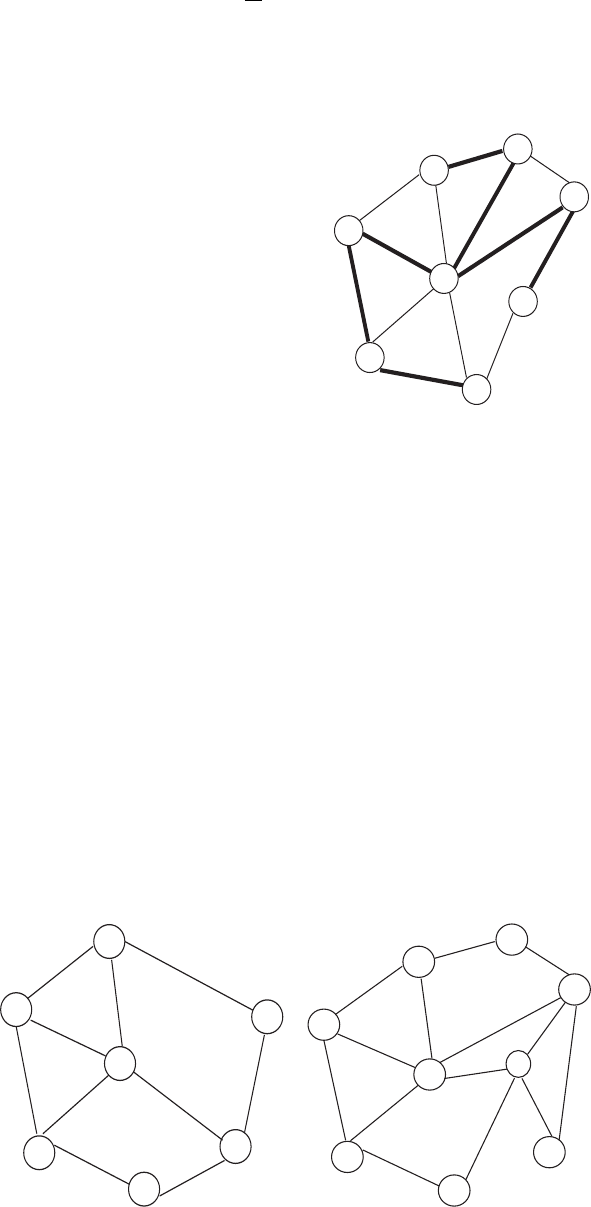
Рис 3.2.7. Итерационный процесс построения минимальной сети
3.3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 87
Итерация 7. Итерационный процесс дает на итерации 5 следующие результаты,
необходимо связать множество T и узел {7}. Получаем связные множества
T = {S, 2, 3, 4, 5, 6, 1, 7}, T = {∅}.
6
1
S
2
3
7
7
4
5
4
2
4
5
2
8
6
7
1
6
3
3
6
Рис 3.2.8. Итерационный процесс построения минимальной сети
Поскольку все узлы связаны, процедура завершается. Минимальная длина кабеля,
соединяющего точку подключения к сети интернет с районами-новостройками, равна
2 + 2 + 3 + 1 + 3 + 4 + 6 = 21 километрам.
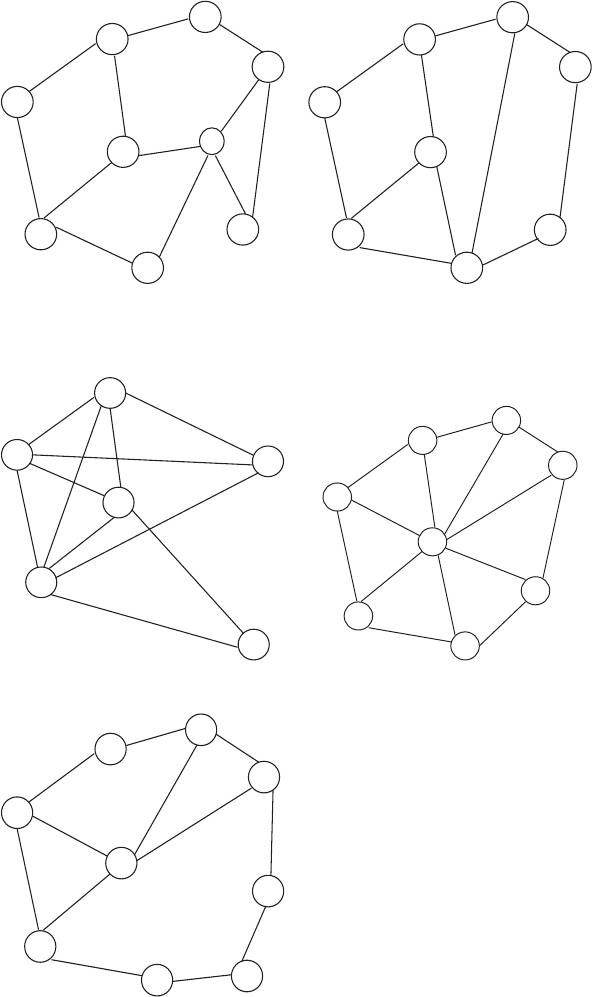
3.3 Задачи для самостоятельного решения
3.3.1 3.3.2
1
S
2
3
S’
7
4
3
5
5
4
2
4
5
4
8
6
1
S
2
3
S’
7
4
7
5
5
4
2
4
5
4
8
6
6
7
8
5
5
10
88 Глава 3. СЕТИ
3.3.3 3.3.4
1
S
2
3
S’
7
4
7
5
4
2
4
5
4
8
6
6
7
8
5
10
1
S
2
3
S’
7
4
2
5
4
2
4
5
4
8
6
1
6
7
3.3.5 3.3.6
2
1
3
4
5
6
7
8
9
10
5
5
6
3
3
1
1
S
2
3
S’
12
10
5
4
10
4
5
6
8
6
6
7
22
8
9
5
15
3.3.7
4
10
1
S
2
3
S’
12
10
4
6
8
6
10
5
22
8
9
7
9
5
Глава 4
Дискретное программирование
4.1 Схема метода ветвей и границ
Метод ветвей и границ применяется при решении задач дискретного программирования
вида:
min
x∈G
φ(x) = φ(x
∗
) = φ
∗
,
где G конечное множество, x
∗
– оптимальное решение, φ
∗
– значение задачи дискретного
программирования.
Метод ветвей и границ относится к группе комбинаторных методов оптимизации.
В основе метода ветвей и границ лежит построение дерева ветвлений. При этом эффек-
тивность применения метода в конкретной задаче определяется тем, насколько оконча-
тельное дерево ветвления отличается от полного дерева.
При реализации метода ветвей и границ необходимо провести следующие построения.
• Оценки. Для любого конечного множества G необходимо уметь строить нижнюю
оценку ε(G), т.е. такую оценку, что
ε(G) ≤ min
x∈G
φ(x).
• Ветвление. Для реализации метода ветвей и границ необходимо разработать про-
цедуру ветвления, т.е. процедуру разбиения множества на систему подмножеств.
Эта процедура задается итеративно.
ИТЕРАЦИЯ 1. Полагаем G
(0)
= G.
89
90 Глава 4. ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ
ИТЕРАЦИЯ 2. Множество G
(0)
заданным способом разбивают на систему подмно-
жеств G
(0)
1
, . . . , G
(0)
r
1
, G
(0)
=
r
1
S
i=1
G
(0)
i
, где
n
G
(0)
i
o
– попарно непересекающаяся система
подмножеств.
ИТЕРАЦИЯ k + 1. Имеются множества G
(k)
1
, . . . , G
(k)
r
, еще не подвергавшиеся ветв-
лению. Выделяем множество G
(k)
i
перспективное для дальнейшего ветвления. По
заданному правилу G
(k)
i
разбивается на систему подмножеств G
(k)
i
1
, . . . , G
(k)
i
r
, G
(k)
i
=
r
S
j=1
G
(k)
i
j
,
n
G
(k)
i
j
o
– попарно непересекающаяся система подмножеств.
Переобозначим множества, не подвергавшиеся ветвлению, как
n
G
(k+1)
p
o
. Перехо-
дим к новой итерации.
Заметим, что на любой итерации объединение множеств, не подвергавшихся ветв-
лению, всегда дает G
(0)
. Понятно, что процедура ветвления завершится за конечное
число итераций, поскольку G
(0)
= G – конечное множество.
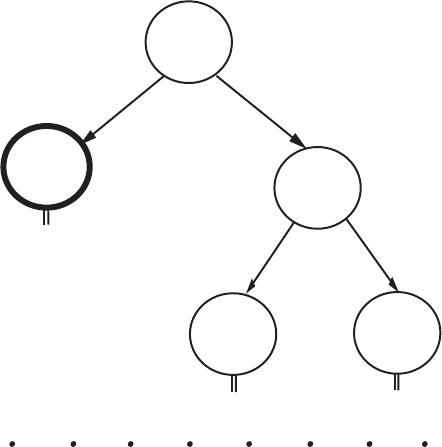
Графически процедура ветвления может быть проиллюстрирована деревом ветв-
ления (рис. 4.1.1).
G
(0)
G
(1)
G
(2)
G
(2)
G
(1)
1
2
21
22
Рис 4.1.1. Дерево ветвления.
• Границы. В процессе ветвления появляются множества, которые не могут быть
подвержены дальнейшему ветвлению. Такие множества называются граничными.
Они являются концевыми вершинами дерева ветвления.
