Зенкевич Н.А. Практикум по исследованию операций
Подождите немного. Документ загружается.


2.4. ПРИМЕРЫ 51
Построим опорный план методом минимального элемента.
Найдем ячейки с минимальными затратами на перевозку единицы продукции, в на-
шем случае это c
12
= c
31
= 5. Этой стоимости сответствуют ячейкам с номерами (1,2) и
(3,1).
Наибольшее значение, которое можно присвоить ячейкам (1, 2) и (3, 1) равно 20. В
этом случае удовлетворяются ограничения, соответствующие первой строке и второ-
му столбцу. Вычеркиваем второй столбец, предложение первой строки и спрос второго
столбца принимают нулевые значения.
Предложение
15 5 25 16 20\ 0
x
11
20 x
13
x
14
17 12 14 25 35
x
21
0 x
23
x
24
5 19 21 23 10
x
31
0 x
33
x
34
Спрос 10\ 20\ 20 15
0 0
Табл.2.4.2. Транспортная таблица.
Следующей ячейкой в незачеркнутой части таблицы становится элемент (3,1). При-
своим ячейке (3,1) значение 10 и вычеркиваем третью строку. Предложение третьей
строки и спрос первого столбца принимают нулевые значения.
Предложение
15 5 25 16 20\
x
11
20 x
13
x
14
17 12 14 25 35
x
21
0 x
23
x
24
5 19 21 23 10\ 0
10 0 0 0
Спрос 10\ 20\ 20 15
0 0
Табл.2.4.3. Транспортная таблица.
Продолжая процедуру далее, присваиваем ячейке (2,3) значение 20. Вычеркиваем

52 Глава 2. ЗАДАЧИ ТРАНСПОРТНОГО ТИПА
третий столбце, корректируем ограничение на предложение, соответствующее второй
строке, 35-20=15.
Продолжая действовать по алгоритму, получаем опорный план X
0
в таблицы таб-
личном виде.
Предложение
15 5 25 16 20\ 0
0 20 0 0
17 12 14 25 35\ 15\ 0
0 0 20 15
5 19 21 23 10\ 0
10 0 0 0
Спрос 10\ 20\ 20\ 15\
0 0 0 0
Табл.2.4.4. Транспортная таблица.
Опорный план X
0
имеет вид:
X
0
=
0 20 0 0
0 0 20 15
10 0 0 0
Суммарные затраты по плану X
0
равны 5 · 20 + 5 · 10 + 14 · 20 + 25 · 15 = 805.
Пример 2.4.2.
Пусть транспортная задача задана транспортной таблицей:
Предложение
15 5 25 16 20
17 12 14 25 35
5 19 21 23 10
Спрос 10 20 20 15
Табл.2.4.5. Транспортная таблица.
Построим опорный план приближенным методом Фогеля (ПМФ). В приведенной ни-
же таблице содержится первый набор штрафов для строк и столбцов.
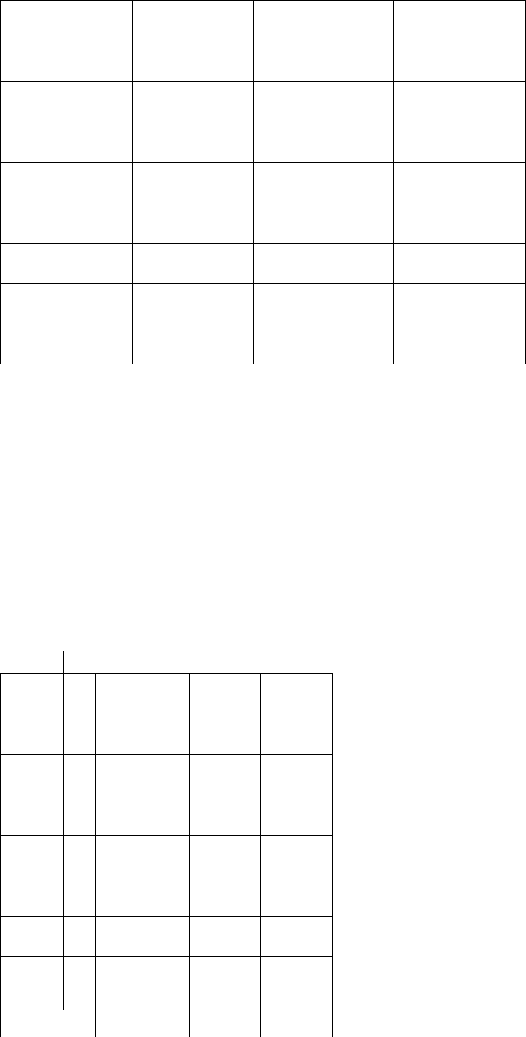
2.4. ПРИМЕРЫ 53
Штрафы для
строк
15 5 25 16 20 15-5=10
17 12 14 25 35 14-12=2
5 19 21 23 10 19-5=14
10 20 20 15
Штрафы
для столбцов 15-5=10 12-5=7 21-14= 7 23-16=7
Табл.2.4.6. Транспортная таблица.
Поскольку третья строка имеет наибольший штраф (=14) и в этой строке ячейка
(3,1) является элементом с наименьшими затратами на перевозку. Этой ячейке присва-
ивается значение 10, при этом полностью выполняются ограничения первого столбца,
его вычеркиваем. Остаток объема производства для третьей строки равен нулю. Новый
набор штрафов представлен в следующей таблице.
Штрафы для строк
15 5 25 16 20 11
0 20
17 12 14 25 35\ 10 2
0
5 19 21 23 10 0 -
10
0 20 20 15
Штрафы
для столбцов – 7 7 9
Табл.2.4.7. Транспортная таблица.
Первой строке соответствует максимальный штраф. Присвоим ячейке (1,2) значе-
ние 20. При этом одновременно выполняются ограничения для первой строки и второго
столбца. Вычеркиваем второй столбец, объем предложения a
1
, соответствующий первой
строке, становится равным нулю.

54 Глава 2. ЗАДАЧИ ТРАНСПОРТНОГО ТИПА
Штрафы для строк
15 5 25 16 0 8
0 20
17 12 14 25 35 11
0 0
5 19 21 23 0 2
10 0
0 20 20 15
Штрафы
для столбцов – - 7 7
Табл.2.4.8. Транспортная таблица.
Максимальные штраф для первой равен 11. Предложение во второй строке равно
35, поэтому полагаем x
23
= 20. Объем предложения, соответствующий второй строке
становится равным 15 (35-20=15). Вычеркиваем третий столбец, так как спрос полностью
удовлетворен.
Применяя метод минимального элемента к последнему столбцу получаем x
24
= 15.
В результате построили опорный план X
0
заданный в виде таблицы.
15 5 25 16
0 20 0 0
17 12 14 25
0 0 20 15
5 19 21 23
10 0 0 0
Табл.2.4.9. Транспортная таблица.
Начальный опорный план X
0
, построенный методом Фогеля имеет вид:
X
0
=
0 20 0 0
0 0 20 15
10 0 0 0
Суммарные затраты по плану X
0
равны 5 · 20 + 5 · 10 + 14 · 20 + 25 · 15 = 805.

2.4. ПРИМЕРЫ 55
Пример 2.4.3.
Заданы вектор производства a = (100, 150, 200, 100), и вектор потребления
b = (120, 200, 100, 30, 100) и матрица C стоимостей перевозки единицы продукта из i
пункта производства A
i
в пункт потребления B
j
:
C =
0, 7 0, 5 0, 6 0, 9 0, 5
0, 4 0, 5 0, 8 0, 8 1, 0
0, 3 0, 2 0, 5 0, 4 0, 4
0, 9 1, 1 1, 0 0, 8 1, 1
Проверяем баланс: 550=550.
Построим начальный опорный план методом северо-западного элемента. В результате
получим:
100\ 0,7 0,5 0,6 0,9 0,5
0 100 0 0 0 0
150\ 0,4 0,5 0,8 0,8 1,0
0 20 130 0 0 0
200\ 0,3 0,2 0,5 0,4 0,4
0 0 70 100 30 0
∗
100\ 0,9 1,1 1,0 0,8 1,1
0 0 0 0 0 100
120\ 200\ 100\ 30\ 100\
0 70 0 0 0
Табл.2.4.10. Транспортная таблица.
Таким образом начальный опорный план задачи X
0
выглядит следующим образом:
X
0
=
100 0 0 0 0
20 130 0 0 0
0 70 100 30 0
0 0 0 0 100
В нашем случае в опорном плане семь положительных элементов, следовательно по-
лученный опорный план является вырожденным, так опорный план является невырож-
денным если число положительных элементов матрицы равно m + n − 1 = 8. В случае

56 Глава 2. ЗАДАЧИ ТРАНСПОРТНОГО ТИПА
вырожденности выделяем среди нулей – базисный ноль, так чтобы могли быть опреде-
лены потенциалы u
i
, v
j
. Пусть в нашем случае это будет элемент x
35
. В транспортной
таблице будем его обозначать как 0
∗
.
Строим множество S
0
= {(i, j)|x
0
ij
> 0} = {(1, 2), (2, 1), (2, 2), (3, 2), (3, 3), (3, 4), (3, 5), (4, 5)}.
Строим систему потенциалов для начального опорного плана. Вводим переменные-
потенциалы u
i
, i = 1, 4 и v
j
, j = 1, 5. Для каждой базисной переменной x
ij
, (i, j) ∈ S
0
потенциалы u
i
и v
j
должны удовлетворять системе уравнений:
v
j
− u
i
= c
ij
, (i, j) ∈ S
0
;
В нашем случае получаем следующую систему потенциалов:
v
1
− v
1
= 0, 7, v
0
1
− u
0
2
= 0, 4,
v
0
2
− u
0
2
= 0, 5, v
0
2
− u
0
3
= 0, 2,
v
0
3
− u
0
3
= 0, 5, v
0
4
− u
0
3
= 0, 4,
v
0
5
− u
0
3
= 0, 4, v
0
5
− u
0
4
= 1, 1.
Находим v
0
i
, j =
1, n, u
j
, i = 1, m – решение данной системы потенциалов. Тогда потен-
циалы плана X
0
= {x
0
ij
} равны:
u
0
1
= 0, v
0
1
= 0, 7, v
0
2
= 0, 8,
v
0
3
= 1, 1, v
0
4
= 1, 0, v
0
5
= 1, 0,
u
0
2
= 0, 3, u
0
3
= 0, 6, u
0
4
= −0, 1.
Для всех небазисных x
ij
, (i, j) /∈ S
0
построим оценки ∆
ij
= c
ij
− (v
0
j
− u
0
i
). После вычис-
лений получаем матрицу невязок ∆
0
= {δ
0
ij
}:
∆
0
=
0 −0, 3 −0, 5 −0, 1 −0, 5,
0 0 0 0, 1 0, 3,
0, 2 0 0 0 0
0, 1 0, 2 −0, 2 −0, 3 0
Если бы δ
ij
≥ 0, i =
1, m, j = 1, n, то X
0
= {x
0
ij
} – оптимальный план транспорт-
ной задачи. Однако у нас имеются отрицательные δ
ij
. Следовательно план не является
оптимальным.
Найдем минимальный отрицательный элемент в матрице невязок ∆
0
= {δ
0
ij
} =
= {c
ij
− (v
0
j
− u
0
i
)}, (переменная, соответствующая этому элементу вводится в число
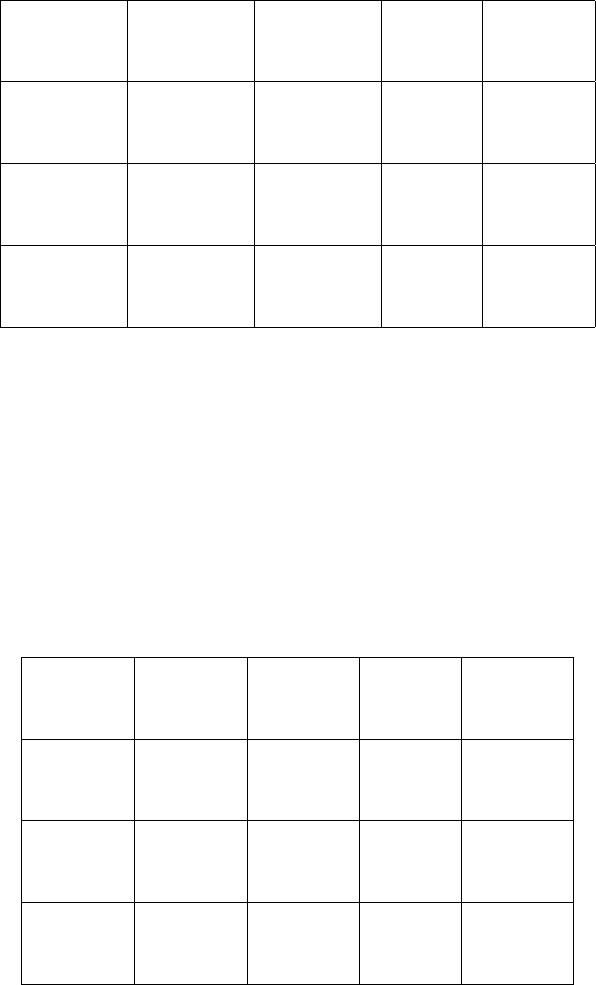
2.4. ПРИМЕРЫ 57
базисных переменных). Минимальный отрицательный элемент матрицы есть δ
0
13
= −0, 5
(если есть несколько одинаковых значений).
Рассматриваем этот элемент и все базисные перевозки плана X
0
= {x
0
ij
}. Элемент
транспортной таблицы x
13
= Θ
+
, который соответствует оценке δ
13
, будет базовым для
построения цикла. Элементы, входящие в цикл отмечены знаками "+"и "−"на следу-
ющей транспортной таблице. В каждой строке и каждом столбце должен быть только
один элемент с "+"и один элемент с "−".
0,7 0,5 0,6 0,9 0,5
100
−
0 Θ
+
0 0
0,4 0,5 0,8 0,8 1,0
20
+
130
−
0 0 0
0,3 0,2 0,5 0,4 0,4
0 70
+
100
−
30 0
∗
0,9 1,1 1,0 0,8 1,1
0 0 0 0 100
Табл.2.4.11. Построение цикла в плане X
0
= {x
0
ij
}.
Пропускаем максимально возможный поток по построенному циклу в плане X
0
=
{x
0
ij
}. Получаем новый план X
1
= {x
1
ij
}.
Величина максимально возможного транспортного потока Θ
+
= min{100, 130, 100} =
100, пропустим Θ
+
= 100 через цикл, то есть прибавим к элементам со знаком "+"и
вычтем из элементов со знаком "−". В результате получим новую транспортную таблицу,
соответствующую плану X
1
= {x
1
ij
}:
0,7 0,5 0,6 0,9 0,5
0
∗
0 100 0 0
0,4 0,5 0,8 0,8 1,0
120 30 0 0 0
0,3 0,2 0,5 0,4 0,4
0 170 0 30 0
∗
0,9 1,1 1,0 0,8 1,1
0 0 0 0 100
Табл.2.4.12. План перевозок X
1
= {x
1
ij
}.
58 Глава 2. ЗАДАЧИ ТРАНСПОРТНОГО ТИПА
Переходим к рассмотрению следующей итерации, начинающейся в п.1, но только с
планом X
1
= {x
1
ij
}.
План X
1
= {x
1
ij
} является врожденным, введем еще один базисный ноль. В качестве
еще одного базисного нулевого элемента возьмем элемент x
11
.
Строим множество S
1
= {(i, j)|x
1
ij
> 0} = {(1, 1), (1, 3), (2, 1), (2, 2), (3, 2), (3, 4),
(3, 5), (4, 5)}.
Для новой транспортной таблицы строим систему потенциалов:
v
1
1
− u
1
1
= 0, 7, v
1
1
− u
1
2
= 0, 4
v
1
2
− u
1
2
= 0, 5, v
1
2
− u
1
3
= 0, 2
v
1
3
− u
1
1
= 0, 6, v
1
4
− u
1
3
= 0, 4
v
1
5
− u
1
3
= 0, 4, v
1
5
− u
1
4
= 1, 1.
Потенциалы плана X
1
= {x
1
ij
} равны:
u
1
1
= 0, v
1
1
= 0, 7, v
1
2
= 0, 8,
v
1
3
= 0, 6, v
1
4
= 1, v
1
5
= 1,
u
1
2
= 0, 3, u
1
3
= 0, 6, u
1
4
= −0, 1.
Для всех небазисных x
ij
, (i, j) /∈ S
0
построим оценки ∆
ij
= c
ij
− (v
0
j
− u
0
i
). После
вычислений получаем матрицу невязок ∆
1
= {δ
1
ij
}:
∆
ij
=
0 −0, 3 0 −0, 1 −0, 5
0 0 0, 5 0, 1 0, 3
0, 2 0 0, 5 0 0
0, 1 0, 2 0, 3 −0, 3 0
Минимальный отрицательный элемент матрицы невязок есть δ
1
15
= −0, 5, следовательно
в клетку (1,5) записываем Θ
+
.
Пропускаем максимально возможный поток Θ
+
= 0 по построенному циклу в плане
X
1
= {x
1
ij
}.

2.4. ПРИМЕРЫ 59
0,7 0,5 0,6 0,9 0,5
0
∗
−
0 100 0 Θ
+
0,4 0,5 0,8 0,8 1,0
120
+
30
−
0 0 0
0,3 0,2 0,5 0,4 0,4
0 170
+
0 30 0
∗
−
0,9 1,1 1,0 0,8 1,1
0 0 0 0 100
Табл.2.4.13. Построение цикла в плане X
1
= {x
1
ij
}.
В результате получим транспортную таблицу, соответствующую плану X
2
= {x
2
ij
}:
0,7 0,5 0,6 0,9 0,5
0
∗
0 100 0 0
∗
0,4 0,5 0,8 0,8 1,0
120 30 0 0 0
0,3 0,2 0,5 0,4 0,4
0 170 0 30 0
0,9 1,1 1,0 0,8 1,1
0 0 0 0 100
Табл.2.4.14. План перевозок X
2
= {x
2
ij
}.
X
2
= {x
2
ij
} – вырожденный план, в качества базисных нулевых элементов используем
элементы x
15
, x
35
.
Строим множество S
2
= {(i, j)|x
2
ij
> 0} = {(1, 3), (1, 5), (2, 1), (2, 2), (3, 2), (3, 4), (3, 5), (4, 5)}
Продолжая итерационный процесс строим систему потенциалов для плана перевозок
X
2
= {x
2
ij
}:
v
2
3
− u
2
1
= 0, 6, v
2
5
− u
2
1
= 0, 5,
v
2
1
− u
2
2
= 0, 4 v
2
2
− u
2
2
= 0, 5,
v
2
2
− u
2
3
= 0, 2, v
2
4
− u
2
3
= 0, 4,
v
2
5
− u
2
3
= 0, 4, v
2
5
− u
2
4
= 1, 1.
Потенциалы плана X
2
= {x
2
ij
} равны:
u
2
1
= 0, v
2
1
= 0, 2, v
2
2
= 0, 3,
v
2
3
= 0, 7, v
2
4
= 0, 5, v
2
5
= 0, 5,
u
2
2
= −0, 2, u
2
3
= 0, 1, u
2
4
= −0, 6.

60 Глава 2. ЗАДАЧИ ТРАНСПОРТНОГО ТИПА
Строим матрицу невязок ∆
2
= {δ
2
ij
}:
0, 5 0, 2 0 0, 4 0
0 0 −0, 1 0, 1 0, 3
0, 2 0 −0, 1 0 0
0, 1 0, 2 −0, 3 −0, 3 0
Возьмем в качестве минимального отрицательного элемента матрицы невязок δ
2
44
=
−0, 3, на место элемента x
44
помещаем Θ
+
строим цикл:
0,7 0,5 0,6 0,9 0,5
0
−
0 100 0 0
∗
0,4 0,5 0,8 0,8 1,0
120 30 0 0 0
0,3 0,2 0,5 0,4 0,4
0 170 0 30
−
0
∗
+
0,9 1,1 1,0 0,8 1,1
0 0 0 Θ
+
100
−
Табл.2.4.15. Построение цикла в плане X
2
= {x
2
ij
}.
Пропускаем максимально возможный поток Θ
+
= 30 по построенному циклу в плане
X
2
= {x
2
ij
}. Новый план X
3
= {x
3
ij
}:
0,7 0,5 0,6 0,9 0,5
0 0 100 0 0
∗
0,4 0,5 0,8 0,8 1,0
120 30 0 0 0
0,3 0,2 0,5 0,4 0,4
0 170 0 0 30
0,9 1,1 1,0 0,8 1,1
0 0 0 30 70
Табл.2.4.16. План перевозок X
2
= {x
2
ij
}
План перевозок X
3
= {x
2
ij
} – вырожденный, в качестве базисного нулевого элемента
оставляем x
15
.
Строим множество S
3
= {(i, j)|x
3
ij
> 0} = {(1, 3), (1, 5), (2, 1), (2, 2), (3, 2), (3, 5), (4, 4), (4, 5)}
