Зенкевич Н.А. Практикум по исследованию операций
Подождите немного. Документ загружается.

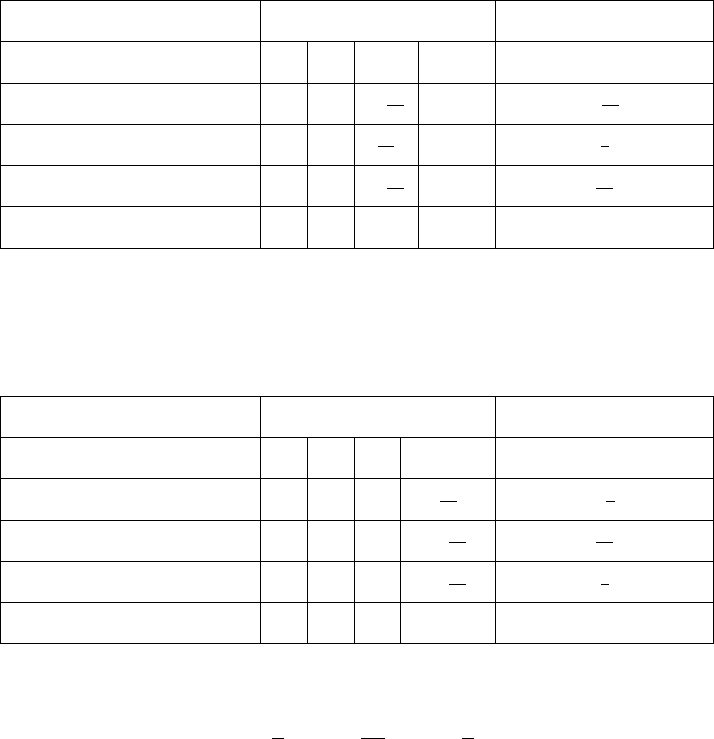
1.4. ДВУХФАЗНЫЙ СИМПЛЕКС-МЕТОД 31
После вычеркивания строки, соответствующей функции −r, и столбцов, соответству-
ющих искусственным переменным, получаем таблицу для второй фазы.
Фаза 2.
Переменные задачи
Базисные переменные x
1
x
2
x
3
x
4
Базисное решение
−z 0 0 −
1
10
0 3
3
10
x
1
1 0
1
10
0
4
5
x
2
0 1 −
3
10
0
1
10
x
4
0 0 1 1 1
Полученная симплексная таблица не двойственно-допустима, переменная x
3
подле-
жит введению в базис, получаем новую таблицу.
Переменные задачи
Базисные переменные x
1
x
2
x
3
x
4
Базисное решение
−z 0 0 0
1
10
3
1
5
x
1
1 0 0 −
1
10
7
10
x
2
0 1 0 −
3
10
2
5
x
3
0 0 1 1 1
После одной итерации симплекс-метода имеем оптимальную таблицу, содержащую
оптимальное решение z
∗
= 3
1
5
; x
∗
1
=
7
10
, x
∗
2
=
2
5
, x
∗
3
= 1.
1.4.2 Задачи для самостоятельного решения
1.4.1 1.4.2
max z = max(2x
1
+ 3x
2
− 5x
3
);
x
1
+ x
2
+ x
3
= 7;
2x
1
− 5x
2
+ x
3
≥ 10;
x
i
≥ 0, i = 1, 2, 3.
min z = min(2x
1
+ 3x
2
− 5x
3
);
x
1
+ x
2
+ x
3
= 7;
2x
1
− 5x
2
+ x
3
≥ 10;
x
i
≥ 0, i = 1, 2, 3.
32 Глава 1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
1.4.3 1.4.4
max z = max(2x
1
+ 4x
2
+ 4x
3
− 3x
4
);
x
1
+ x
2
+ x
3
= 4;
x
1
+ 4x
2
+ x
4
= 8;
x
i
≥ 0, i = 1, 2, 3, 4.
max z = max(x
1
+ 5x
2
+ 3x
3
);
x
1
+ 2x
2
+ x
3
= 3;
2x
1
− x
2
= 4;
x
i
≥ 0, i = 1, 2, 3.
1.4.5 1.4.6
min z = min(−3x
1
+ 6x
2
);
5x
1
− 2x
2
≤ 4,
4x
1
− 2x
2
≥ −4,
x
1
+ x
6
≥ 4;
x
i
≥ 0, i = 1, 2, 3.
min z = min(−2x
1
+ x
2
);
2x
1
+ x
2
≤ 8,
3x
1
+ 3x
2
≥ 6,
3x
1
+ x
2
≥ 3;
x
i
≥ 0, i = 1, 2.
1.4.7 1.4.8
min z = min(−2x
1
+ x
2
);
2x
1
+ x
2
≤ 8,
x
1
+ x
2
≥ 6,
−3x
1
+ 2x
2
≥ 3;
x
i
≥ 0, i = 1, 2.
min z = min(−3x
1
+ 2x
2
);
x
1
+ 2x
2
≥ 10,
3x
1
+ x
2
≥ 15;
x
i
≥ 0, i = 1, 2.
1.4.9 1.4.10
max z = max(3x
1
+ 3x
2
);
x
1
+ x
2
≤ 4;
3x
1
+ x
2
≥ 4;
x
1
+ 5x
2
≥ 4;
0 ≥ x
1
≤ 3,
0 ≥ x
2
≤ 3.
max z = max(x
1
+ x
2
);
5x
1
− 2x
2
≤ 4;
x
1
− 2x
2
≥ −4;
x + x
2
≥ 4;
x
1
, x
2
≥ 0.
1.4.11 1.4.12
max z = max(2x
1
− x
2
);
x
1
− x
2
≥ −3,
6x
1
+ 7x
2
≤ 42,
2x
1
− 3x
2
≤ 6;
x
1
, x
2
≥ 0.
max z = max(7x
1
+ 5x
2
);
7x
1
+ 5x
2
≥ 7,
7x
1
− 5x
2
≥ 35,
x
1
− 5x
2
≤ 0;
x
1
, x
2
≥ 0.
1.4. ДВУХФАЗНЫЙ СИМПЛЕКС-МЕТОД 33
1.4.13 1.4.14
max z = max(2x
1
− 3x
2
);
5x
1
+ 2x
2
≥ 10,
x
1
+ 3x
2
≤ 12;
x
1
, x
2
≥ 0.
min z = min(−2x
1
+ x
2
);
x
1
+ x
2
≤ 6,
−3x
1
+ 2x
2
≥ 3,
x
1
, x
2
≥ 0.
1.4.15 1.4.16
min z = min(6x
1
+ 4x
2
);
2x
1
+ x
2
≥ 3,
x
1
− x
2
≤ 1;
x
1
, x
2
≥ 0.
min z = min(4x
1
+ 15x
2
+ 12x
3
+ 2x
4
);
2x
2
+ 3x
3
+ x
4
≥ 1,
x
1
+ 3x
2
+ x
3
− x
4
≥ 1,
x
1
, x
2
, x
3
, x
4
≥ 0.

34 Глава 1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
1.5 Двойственность в линейном программировании
Для каждой задачи ЛП ( прямой задачи) можно однозначно построить другую задачу
ЛП, называемую двойственной задачей, которая строится по следующим правилам:
1. Каждому ограничению прямой задачи (ПЗ) соответствует переменная двойствен-
ной задачи (ДЗ) и наоборот.
2. Коэффициенты целевой функции прямой задачи становятся свободными членами
ограничений двойственной задачи и наоборот.
3. Если прямая задача – задача максимизации, то двойственная – задача минимиза-
ции.
Переменные Переменные ПЗ Коэффициенты
ДЗ x
1
. . . x
j
. . . x
n
целевой функции
ДЗ
Коэффициенты целевой функции ПЗ
c
1
. . . c
j
. . . c
n
y
1
a
11
. . . a
1j
. . . a
1n
b
1
. . . . . . . . .
y
i
a
i1
. . . a
ij
. . . a
in
b
i
. . . . . . . . .
y
m
a
m1
. . . a
mj
. . . a
mn
b
m
ПЗ – задача максимизации ДЗ – задача минимизации
Табл.1.5.1. Соответствие элементов прямой и двойственной задач
4. Ограничениям типа стандартных неравенств ПЗ соответствуют неотрицательные
переменные ДЗ, ограничениям типа равенств ПЗ – переменные ДЗ, на знак которых
не наложены ограничения и наоборот.

1.5. ДВОЙСТВЕННОСТЬ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ 35
Задача максимизации Задача минимизации
Ограничения Переменные
≥ ≤ 0
≤ ≥ 0
= переменная не имеет ограничений
на знак
Переменные Ограничения
≥ 0 ≥
≤ 0 ≤
переменная не имеет ограничений =
на знак
Табл.1.5.2. Соответствие знаков переменных и ограничений прямой задачи и двой-
ственной задачи.
Пусть прямая задача линейного программирования представляет собой общую задачу
максимизации:
max z = max(c
1
x
1
+ c
2
x
2
+ . . . + c
n
x
n
); (1.5.1)
a
i1
x
1
+ a
i2
x
2
+ . . . + a
in
x
n
= b
i
, i = 1, k;
a
i1
x
1
+ a
i2
x
2
+ . . . + a
in
x
n
≤ b
i
, i =
k + 1, m.
x
j
≥ 0, j =
1, p, x
j
≥≤ 0, j = p + 1, n,
(1.5.2)
где x
j
– переменные прямой задачи.
Применяя правила написания двойственной задачи, получаем следующую двойствен-
ную задачу:
min ω = min(b
1
y
1
+ b
2
y
2
+ . . . + b
m
y
m
); (1.5.3)
a
1j
y
1
+ a
2j
y
2
+ . . . + a
mj
y
n
≥ c
j
, j = 1, p;
a
1j
y
1
+ a
2j
y
2
+ . . . + a
mj
y
n
= c
j
, i = p + 1, n.
y
i
≥≤ 0, i =
1, k, y
i
≥ 0, i = k + 1, m,
(1.5.4)
где y
i
– переменные двойственной задачи.
Понятно, что двойственной для двойственной задачи будет прямая задача.
Пример.
Рассмотрим прямую задачу ЛП:

36 Глава 1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
max z = max(5x
1
+ 12x
2
+ 4x
3
);
x
1
+ 2x
2
+ x
3
≤ 10;
x
1
− x
2
+ 2x
3
= 8;
3x
1
+ 2x
2
≥ 3;
x
2
≤ 0, x
3
≥ 0.
Тогда двойственной задачей будет следующая:
min z = min(10y
1
+ 8y
2
+ 3y
3
);
y
1
+ y
2
+ 3y
3
= 5;
2y
1
− y
2
+ 2y
3
≤ 12;
y
1
+ 2y
2
≥ 4;
y
1
≥ 0, y
3
≤ 0.
Частные случаи прямой и двойственной задач в векторной форме
Прямая задача ЛП Двойственная задача ЛП
max z = max CX
AX ≤ B
X ≥ 0
min w = min BY
Y A ≥ C
Y ≥ 0
max z = max CX
AX = B
X ≥ 0
min w = min BY
Y A ≥ C
min z = min CX
AX ≤ B
max w = max BY
Y A = C
Y ≤ 0
min z = min CX
AX = B
X ≥ 0
max w = max BY
Y A ≤ C
min z = min CX
AX ≥ B
X ≥ 0
max w = max BY
Y A ≤ C
Y ≥ 0
1.5. ДВОЙСТВЕННОСТЬ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ 37
Рассмотрим пару двойственных задач, например в стандартной форме:
max z = max CX
AX ≤ B
X ≥ 0
↔
min w = min BY
Y A ≥ C
Y ≥ 0
Свойство допустимых решений пары двойственных задач.
Пусть X и Y – допустимые решения задач ЛП в стандартной форме. Тогда для
значений целевых функций справедливо неравенство: CX ≤ BY .
Теорема двойственности в линейном программировании
Теорема 1.5.1 Если обе задачи прямая и двойственная имеют допустимые решения,
то обе зад ачи прямая и двойственная имеют оптимальные решения, причем z
∗
=
w
∗
, где z
∗
= CX
∗
, ω
∗
= BY
∗
.
Если хотя бы одна из задач прямая или двойственная не имеет допустимого реше-
ния, то обе задачи прямая и двойственная не имеют оптимального решения.
Критерий оптимальности (следствие теоремы двойственности).
Для того чтобы пара допустимых решений X
∗
и Y
∗
двойственных задач была па-
рой оптимальных решений соответствующих задач необходимо и достаточно, чтобы
выполнялось равенство CX
∗
= BY
∗
.
Стандартная теорема равновесия (критерий оптимальности)
Теорема 1.5.2 Для того чтобы пара допустимых решений X
∗
и Y
∗
двойственных за-
дач в стандартной форме была парой оптимальных решений соответствующих зада ч
необходимо и достаточно, чтобы выполнялись равенства:
Y
∗
(B − AX
∗
) = 0;
(Y
∗
A − C)X
∗
= 0.
Рассмотрим пару двойственных задач вида, (прямая задача в канонической форме):
max z = max CX
AX = B
X ≥ 0
↔
min w = min BY
Y A ≥ C

38 Глава 1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Каноническая теорема равновесия (критерий оптимальности)
Теорема 1.5.3 Для того чтобы пара допустимых решений X
∗
и Y
∗
данной пары двой-
ственных задач была парой оптимальных решений соответствующих задач необходи-
мо и достаточно, чтобы выполнялось равенство:
(Y
∗
A − C)X
∗
= 0.
1.6 Двойственный симплекс-метод
Рассмотрим каноническую задачу ЛП максимизации:
max z = max(c
1
x
1
+ c
2
x
2
+ . . . + c
n
x
n
); (1.6.1)
a
i1
x
1
+ a
i2
x
2
+ . . . + a
in
x
n
= b
i
, i =
1, m;
x
j
≥ 0, j = 1, n.
(1.6.2)
Тогда соответствующая система линейных уравнений имеет вид:
z − (
c
1
x
1
+ c
2
x
2
+ . . . + c
n
x
n
) = 0; (1.6.3)
a
i1
x
1
+ a
i2
x
2
+ . . . + a
in
x
n
= b
i
, i = 1, m;
x
j
≥ 0, j =
1, n.
(1.6.4)
Приводим систему к диагональной форме по переменным z
0
, x
1
, . . . , x
m
:
z + . . . + c
m+1
x
m+1
+ . . . + c
s
x
s
+ . . . + c
n
x
n
= z
0
x
1
+ . . . + a
1,m+1
x
1,m+1
+ . . . + a
1,s
x
1,s
+ . . . + a
1,n
x
1,n
= b
1
;
. . . . . . . . .
x
r
+ . . . + a
r,m+1
x
r,m+1
+ . . . + a
r,s
x
r,s
+ . . . + a
r,n
x
r,n
= b
r
;
. . . . . . . . .
x
m
+ . . . + a
m,m+1
x
m,m+1
+ . . . + a
m,s
x
m,s
+ . . . + a
m,n
x
m,n
= b
m
.
(1.6.5)
Составим из коэффициентов диагональной формы симплексную таблицу:

1.6. ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД 39
z x
1
. . . x
r
. . . x
m
x
m+1
. . . x
s
. . . x
n
z z
0
1 . . . 0 . . . 0 c
m+1
. . . c
s
. . . c
s
x
1
b
1
0 . . . 1 . . . 0 a
1,m+1
. . . a
1,s
. . . a
1,n
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
x
r
b
r
0 . . . 0 . . . 0 a
r,m+1
. . . a
r,s
. . . a
r,n
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
x
m
b
m
0 . . . 0 . . . 1 a
m,m+1
. . . a
m,s
. . . a
m,n
Двойственный симплекс-метод начинает вычисления с двойственно допустимой
симплексной таблицы и сохраняет таблицу двойственно допустимой на протяжении всех
итераций. Двойственный симплекс-метод реализуется посредством таких же таблиц, что
и прямой симплекс-метод.
Алгоритм двойственного симплекс-метода.
0. Условие двойственной допустимости. Начать вычисления с двойственно-допустимой
симплексной таблицы, т.е. таблицы, в которой все элементы нулевой строки неотрица-
тельны:
c
j
≥ 0, j =
1, n.
Двойственная допустимость сохраняется в процессе всех вычислений (на всех итераци-
ях).
ИТЕРАЦИЯ
1. Проверка оптимальности или нахождение ведущей строки симплексной
таблицы.
• Если b
i
≥ 0, i =
1, m, (таблица прямо допустима), то текущее решение опти-
мально.
• в задаче ЛП в качестве выводимой из базиса переменной x
r
выбирается та
переменная для которой выполняется:
b
r
= min
b
i
<0
b
i
.
Строка с номером r называется ведущей строка симплексной таблицы.

40 Глава 1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
2. Проверка неограниченности решения и выбор ведущего столбца (веду-
щего элемента) симплексной таблицы.
Если в ведущей строке все коэффициенты a
rj
≥ 0, то задача ЛП не имеет опти-
мального решения.
3. В противном случае следует выбрать ведущий столбец s из условия:
¯
¯
¯
¯
c
s
a
rs
¯
¯
¯
¯
= min
a
rj
<0
¯
¯
¯
¯
c
j
a
rj
¯
¯
¯
¯
Переменная x
s
– вводится в число базисных переменных. Элемент a
rs
называется
ведущим элементом симплексной таблицы.
4. Преобразование таблицы. С помощью эквивалентных преобразований (метод
Гаусса) сделать так, чтобы ведущий элемент таблицы стал равен 1, а остальные
элементы в ведущем столбце равны 0. Базисная переменная x
r
заменяется на x
s
.
После получения новой симплексной таблицы переходим к пункту 1 новой итера-
ции.
Пример:
min z = min(4x
1
+ 2x
2
);
6x
1
+ 2x
2
≥ 5;
4x
1
+ 3x
2
≥ 7;
x
1
+ 2x
2
≤ 3;
x
1
, x
2
≥ 0.
Приведем задачу к каноническому виду, для этого умножаем первые два неравенства
на -1 и введем слабые переменные в первые два ограничения. В результате получим:
min z = min(4x
1
+ 2x
2
);
−6x
1
− 2x
2
≤ −5;
−4x
1
− 3x
2
≤ −7;
x
1
+ 2x
2
≤ 3;
x
1
, x
2
≥ 0.
