Зенкевич Н.А. Практикум по исследованию операций

Подождите немного. Документ загружается.

4.2. ЗАДАЧА О КОММИВОЯЖЕРЕ 101

будет не меньше n. Из них выберем пару (i

∗

, j

∗

) так, чтобы множество G

, предположи-

тельно содержало оптимальный цикл, а множество G

его не содержало. По построению

, по любому из его циклов путь переходит из города i

∗

в некоторый промежуточный

город k (k 6= i

∗

), а в город j

∗

попадают только из города l (l 6= i

∗

Длина этого пути будет не меньше, чем

Θ(i, j) = min

k6=j

+ min

l6=i

= α

+ β

Остается выбрать пару (i

∗

, j

∗

) так, чтобы Θ(i

∗

, j

∗

) было максимальным:

Θ(i

∗

, j

∗

) = max

i,j

(α

+ β

3. Пересчет оценок и преобразование матрицы расстояний при ветвлении.

В множестве G

запрещен непосредственный переезд из i

∗

в j

∗

. Поэтому матрица,

соответствующая этому множеству, отличается от C

элементом c

∗

, который следует

положить равным ∞. Кроме того, следует запретить возможность образования замкну-

тых подциклов, содержащих меньше чем n городов.

Оценка для множества G

вычисляются по следущей формуле:

ξ(G

) = ξ(G

) + Θ(i

∗

, j

∗

Множество G

по построению содержит непосредственный переход из i

∗

в j

∗

. По-

этому в матрице C

, соответствующей G

, следует вычеркнуть строку i

∗

и столбец j

∗

Применив процедуру приведения к матрице C

, вычислим сумму приводящих констант

. Тогда оценка для множества G

будет равна

ξ(G

) = ξ(G

) + H

Далее для ветвления из множеств G

и G

выбираем то, которое имеет наименьшую

оценку.

102 Глава 4. ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ

4.2.2 Пример 4.2.1.

1 2 3 4 5 6

1 ∞ 27 43 26 30 26

2 7 ∞ 16 1 30 25

3 20 13 ∞ 35 5 0

4 21 16 25 ∞ 18 18

5 12 46 27 48 ∞ 5

6 23 5 5 9 5 ∞

Выполним поцедуру приведения матрицы. Находим приводящие константы h

1 2 3 4 5 6 h

1 ∞ 27 43 16 30 26 16

2 7 ∞ 16 1 30 25 1

3 20 13 ∞ 35 5 0 0

4 21 16 25 ∞ 18 18 16

5 12 46 27 48 ∞ 5 5

6 23 5 5 9 5 ∞ 5

Вычитаем h

из всех элементов соответствующей строк. В результате получим таб-

лицу:

1 2 3 4 5 6

1 ∞ 11 27 0 14 10

2 6 ∞ 15 0 29 24

3 20 13 ∞ 35 5 0

4 5 0 9 ∞ 2 2

5 7 41 22 43 ∞ 0

6 18 0 0 4 0 ∞

5 0 0 0 0 0

В получившейся матрице находим h

в каждом столбце и вычитаем их из каждо-

го элемента соответствующего столбца. В результате процедуры приведения получаем

таблицу:

4.2. ЗАДАЧА О КОММИВОЯЖЕРЕ 103

1 2 3 4 5 6

1 ∞ 11 27 0 14 10

2 1 ∞ 15 0 29 24

3 15 13 ∞ 35 5 0

4 0 0 9 ∞ 2 2

5 2 41 22 43 ∞ 0

6 13 0 0 4 0 ∞

Просуммируем все приводящие константы H

= (16 + 1 + 0 + 16 + 5 + 5) + 5 = 28, это

нижняя оценка всех возможных циклов.

Выбираем все элементы c

матрицы издержек которые равны нулю. В нашем случае

это элементы: c

, c

. Для всех таких элементов построим

длины Θ(i, j) по правилу 2. (Закрываем элемент для которого строим оценку и склады-

ваем минимальный элемент строки и столбца на пересечении которых он находится). В

результате получим:

Θ(1, 4) = 10, Θ(2, 4) = 1, Θ(3, 6) = 5, Θ(4, 1) = 1, Θ(4, 2) = 0, Θ(5, 6) = 2, Θ(6, 2) =

0, Θ(6, 3) = 9, Θ(6, 5) = 2.

Выбираем первую пару городов (1,4), т.к. Θ

∗

(1, 4) = 10 максимальное значение среди

всех Θ

∗

(i, j).Множество G

содержит переход из города 1 в город 4. Множество G

не

содержит непосредственного переходи из первого города в четвертый.

Построим оценки множеств G

, G

и G

ξ(G

) = H

= 48

ξ(G

) = H

+ Θ

∗

(1, 4) = 48 + 10 = 58.

Вычеркиваем первую строку и четвертый столбец в матрице соответствующей мно-

жеству G

, на элемент (4,1) ставим знак запрета ∞, для того чтобы на следующем шаге

не мог образоваться подцикл. Например, если бы на следующем шаге получилась бы

пара городов (4,1), тогда коммивояжер вернулся бы в пункт 1 и не имел возможности

совершить весь маршрут.

Переходим к первому шагу алгоритма, то есть к процедуре приведения матрицы, но

уже для матрицы меньшей размерности.

104 Глава 4. ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ

1 2 3 5 6

2 1 ∞ 15 29 24

3 15 13 ∞ 5 0

4 ∞ 0 9 2 2

5 2 41 22 ∞ 0

6 13 0 0 0 ∞

В результате процедуры приведения на этой итерации получим таблицу:

1 2 3 5 6

2 0 ∞ 14 28 23

3 15 13 ∞ 5 0

4 ∞ 0 9 2 2

5 2 41 22 ∞ 0

6 13 0 0 0 ∞

Сумма приводящих констант H

= 1.

Снова выбираем нулевые элементы c

, c

и вычисляем для них

длины Θ(i, j): Θ(3, 6) = 5, Θ(4, 2) = 2, Θ(5, 6) = 2, Θ(6, 2) = 9, Θ(6, 5) = 2.

Следующая пара городов (2,1), т.к. Θ

∗

(2, 1) = 16 – максимальная из величин Θ(i, j).

Множество G

содержит переход из города 2 в город 1. Множество G

не содержит

непосредственного переходи из второго города в первый.

Строим оценки множеств G

и G

ξ(G

) = ξ(G

) + H

= 48 + 1 = 49

ξ(G

) = ξ(G

) + Θ

∗

(2, 1) = 49 + 16 = 65.

Вычеркиваем вторую строку и первый столбец в матрице, соответствующей множе-

ству G

, ставим запрет на элемент (4,2), иначе на следующей итерации может получиться

подцикл: ((1,4)(4,2)(2,1)).

2 3 5 6

3 13 ∞ 5 0

4 0 9 2 2

5 41 22 ∞ 0

6 0 0 0 ∞

4.2. ЗАДАЧА О КОММИВОЯЖЕРЕ 105

Выполняем процедуру приведения, результате которой получаем приведенную таб-

лицу на второй итерации.

2 3 5 6

3 13 ∞ 5 0

4 ∞ 7 0 0

5 41 22 ∞ 0

6 0 0 0 ∞

Сумма приводящих констант H

= 2. Нулевые элементы приведенной матрицы

, c

. Вычисляем длины: Θ(3, 5) = 5, Θ(4, 5) = 0, Θ(4, 6) = 0,

Θ(5, 6) = 22, Θ(6, 2) = 13, Θ(6, 3) = 7, Θ(6, 5) = 0. Максимальная длина перехода Θ

∗

(5, 6) =

22, следовательно следующая пара городов (5,6).

Множество G

содержит переход из города 5 в город 6. Множество G

не содержит

непосредственного переходи из пятого города в шестой.

На этой итерации получили следующие оценки для множеств G

, G

ξ(G

) = ξ(G

) + H

= 49 + 2 = 51

ξ(G

) = ξ(G

) + Θ

∗

(5, 6) = 51 + 22 = 73.

Вычеркиваем пятую строку и шестой столбец и ставим запрет на элемент ( 6,5).

На новой итерации таблица издержек имеет вид:

2 3 5

3 13 ∞ 5

4 ∞ 7 0

6 0 0 ∞

Процедура приведения дает следующий результат:

2 3 5

3 7 ∞ 0

4 ∞ 7 0

6 0 0 ∞

Сумма приводящих констант H

= 5. Выбираем нулевые элементы на этой итерации:

, c

. Вычисляем длины: Θ(3, 5) = 8, Θ(4, 5) = 7, Θ(6, 2) = 8, Θ(6, 3) = 7, в

106 Глава 4. ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ

случае одинаковых величин Θ(i, j), имеющих максимальное значение выбираем любую.

В нашем случае максимальными являются Θ

∗

(3, 5) = 8 и Θ(6, 2) = 8. Выберем пару

городов городов (3,5), соответствующую Θ

∗

(3, 5) = 8.

Строим оценки множеств G

и G

ξ(G

) = ξ(G

) + H

= 51 + 5 = 56

ξ(G

) = ξ(G

) + Θ

∗

(2, 1) = 56 + 8 = 64.

Вычеркиваем третью строку и пятый столбец и ставим запрет на (6,3), так как име-

ются пары городов (5,6) и (3,6), которые вместе с парой (6,3) могут образовать подцикл.

Новая таблица:

2 3

4 ∞ 7

6 0 ∞

Выполняем приведение и получаем таблицу:

2 3

4 ∞ 0

6 0 ∞

Сумма приводящих констант H

= 7. На этой итерации у нас остались две пары

городов (4,3) и (6,2).

Строим оценки для множеств G

и G

ξ(G

) = ξ(G

) + H

= 56 + 7 = 63

ξ(G

) = ξ(G

) + Θ

∗

(4, 2) = ξ(G

) + Θ

∗

(6, 2) = ∞.

Вычисляем цикл t = ((6, 2), (4, 3), (3, 5), (5, 6), (2, 1), (1, 4)) с суммарными издержками

L(t) = 63.

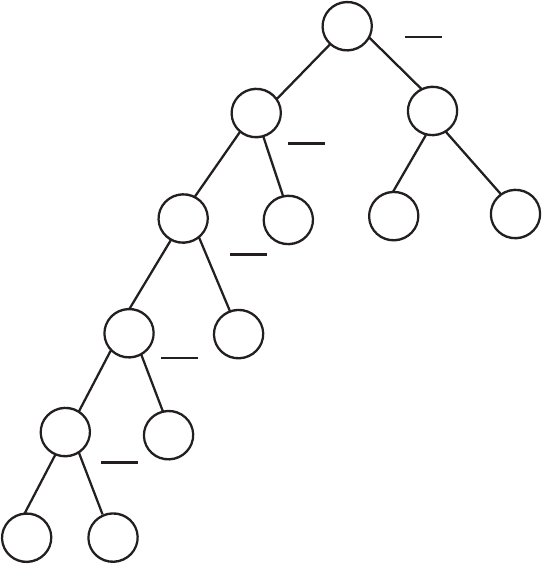
Строим дерево ветвления см. рис. 4.2.1.

Условие оптимальности. Для проверки сравним суммарные издержки на всем марш-

руте с нижними границами концевых множеств в концевой схеме ветвления. При срав-

нении могут получиться два сдучая.

• Суммарные издержки меньше граничных значений. Это означает что найденный

маршрут является искомым и имеет минимальные издержки (минимальную дли-

ну).

4.2. ЗАДАЧА О КОММИВОЯЖЕРЕ 107

• Есть такие концевые множества G

нижние границы которых меньше суммарных

издержек найденного маршрута. В этом случае выбирается множество G

с наи-

меньшей нижней границей и применяем алгоритм начиная с шага 1, предваритель-

но поставив новый запрет в исходную матрицу на место того элемента, который

соответсвует участку маршрута, для концевого множества которого нарушается

условие оптимальности.

В нашем примере условие оптимальности не выполнено, так как значение суммарных

издержек 63 больше, чем стоимость проезда по запрещенному участку (4,1), которая

равна 58, поэтому возвращаемся на этот этап, ставим запрет на (1,4), и в этих условиях

решаем исходную задачу. Начинаем ветвить множество G

1 2 3 4 5 6

1 ∞ 27 43 ∞ 30 26

2 7 ∞ 16 1 30 15

3 20 13 ∞ 35 5 0

4 21 16 25 ∞ 18 18

5 12 46 27 48 ∞ 5

6 23 5 5 9 5 ∞

Процедура приведения:

1 2 3 4 5 6 h

1 ∞ 27 43 ∞ 30 26 26

2 7 ∞ 16 1 30 15 1

3 20 13 ∞ 35 5 0 0

4 21 16 25 ∞ 18 18 16

5 12 46 27 48 ∞ 5 5

6 23 5 5 9 5 ∞ 5

1 2 3 4 5 6

1 ∞ 1 17 ∞ 4 0

2 6 ∞ 15 0 29 24

3 20 13 ∞ 35 5 0

4 5 0 9 ∞ 2 2

5 7 41 22 43 ∞ 0

6 18 0 0 4 0 ∞

5 0 0 0 0 0

В результате приведения матрицы издержек получили:

108 Глава 4. ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ

1 2 3 4 5 6

1 ∞ 1 17 ∞ 4 0

2 1 ∞ 15 0 29 24

3 15 13 ∞ 35 5 0

4 0 0 9 ∞ 2 2

5 2 41 22 43 ∞ 0

6 13 0 0 4 0 ∞

Сумма новых приводящих констант H

= 58, нулевые элементы в этом случае следу-

ющие: c

, c

. Строим длины: Θ(1, 6) = 1, Θ(2, 4) = 5, Θ(3, 6) =

5, Θ(4, 1) = 1, Θ(4, 2) = 0, Θ(5, 6) = 2, Θ(6, 2) = 0, Θ(6, 3) = 9, Θ(6, 5) = 2.

В этом случае первая пара городов (6,3), т.к. этой паре городов соответствует макси-

мальная длина Θ

∗

(6, 3) = 9.

Множество G

содержит переход из города 6 в город 3. Множество G

не содержит

непосредственного переходи из шестого города в третий.

Следовательно вычеркиваем шестую строку и третий столбец, и ставим запрет на

элемент (3,6).

Вычисляем оценки для множеств G

и G

ξ(G

) = H

= 58

ξ(G

) = ξ(G

) + Θ

∗

(6, 3) = 67.

Снова выполняем процедуру приведения и получаем таблицу:

1 2 4 5 6

1 ∞ 1 ∞ 4 0 0

2 1 ∞ 0 29 24 0

3 15 13 35 5 ∞ 5

4 0 0 ∞ 2 2 0

5 2 41 43 ∞ 0 0

Сумма приводящих констант H

= 5.

Вычислим оценки G

и G

ξ(G

) = ξ(G

) + H

= 58 + 5 = 63

4.2. ЗАДАЧА О КОММИВОЯЖЕРЕ 109

Мы видим, что оценка ξ уже равна 63, хотя пройден не весь маршрут, и значит в

дальнейшем оценки ξ(G

) будут возрастать. Значит построенный ранее цикл является

оптимальным.

(1,4)

(2,1)

(5,6)

(3,5)

(6,3)

(1,4)

(2,1)

(5,6)

(3,5)

(6,3)

∞

Рис 4.2.1. Дерево ветвления.

4.2.3 Задачи для самостоятельного решения

4.2.1







∞ 68 73 24 70 9

58 ∞ 16 44 11 92

63 9 ∞ 86 13 18

17 34 76 ∞ 52 70

60 18 3 45 ∞ 58

16 82 11 60 48 ∞







4.2.2







∞ 4 10 13 4 8

2 ∞ 9 7 6 7

8 5 ∞ 5 5 9

5 8 5 ∞ 7 10

6 4 4 9 ∞ 4

5 1 4 8 3 ∞







4.2.3







∞ 21 40 28 60 52

58 ∞ 11 39 22 56

22 12 ∞ 23 14 19

25 47 51 ∞ 20 54

47 43 18 42 ∞ 52

44 49 50 52 29 ∞







4.2.4







∞ 6 56 35 48 29

34 ∞ 46 46 55 26

29 31 ∞ 32 13 42

26 34 12 ∞ 17 7

38 35 40 13 ∞ 47

60 25 59 36 31 ∞







110 Глава 4. ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ

4.2.5







∞ 44 60 54 29 39

53 ∞ 46 19 42 6

36 7 ∞ 37 44 3

21 47 49 ∞ 14 26

15 12 38 46 ∞ 24

19 6 45 57 11 ∞







4.2.6







∞ 14 40 33 16 51

48 ∞ 34 4 11 24

57 35 ∞ 24 38 52

30 50 44 ∞ 9 31

18 42 24 31 ∞ 30

1 38 31 19 32 ∞







4.2.7







∞ 41 60 39 46 10

31 ∞ 59 16 1 51

29 51 ∞ 14 42 50

35 12 52 ∞ 16 26

16 39 15 60 ∞ 57

15 30 38 47 36 ∞







4.2.8







∞ 4 39 22 10 47

58 ∞ 56 18 4 35

34 29 ∞ 17 57 18

52 4 22 ∞ 15 37

41 44 25 11 ∞ 32

11 6 19 2 58 ∞







4.2.9







∞ 56 48 39 3 40

47 ∞ 50 4 10 49

48 50 ∞ 42 19 16

24 44 47 ∞ 23 33

38 17 6 51 ∞ 26

29 56 55 34 18 ∞







4.2.10







∞ 16 13 35 41 52

19 ∞ 29 31 26 18

57 51 ∞ 44 51 7

5 40 32 ∞ 14 16

33 41 28 3 ∞ 53

19 54 24 10 41 ∞







4.2.11







∞ 22 26 56 38 60

34 ∞ 12 51 37 27

45 33 ∞ 44 47 37

39 7 16 ∞ 57 8

35 56 40 58 ∞ 27

9 20 36 31 18 ∞







4.2.12







∞ 41 27 54 46 5

42 ∞ 11 32 58 21

36 5 ∞ 33 22 33

46 24 59 ∞ 49 59

48 58 11 44 ∞ 47

26 50 35 19 27 ∞





