Zdunkowski W., Trautmann T., Bott A. Radiation in the atmosphere: A course in Theoretical Meteorology
Подождите немного. Документ загружается.


8.4 Vibrations and rotations of molecules 315
It turns out that the harmonic oscillator approximation is a good approximation
only in the neighborhood of the equilibrium value of r. A more refined approx-
imation is the Morse function as introduced in (8.146). Substituting (8.146) into
(8.187) yields a new solution for the frequency
˜ν =
E
hc
= ˜ν
e
v +
1
2
− x
e
˜ν
e
v +
1
2
2
+ J(J + 1)B
e
− J
2
(J + 1)
2
D
e
− α
e
v +
1
2
J (J + 1)
(8.189)
where
˜ν
e
=
β
2πc
2D
µ
1/2
, D
e
=
h
3
128π
6
µ
3
˜ν
2
e
c
3
r
6
e
, B
e
=
h
8π
2
Ic
x
e
=
h ˜ν
e
c
4D
, α
e
=
3h
2
˜ν
e
16π
2
µr
2
e
D
1
βr
e
−
1
β
2
r
2
e
(8.190)
Since we have divided the energy E by hc, (8.189) is expressed in wave numbers.
For most diatomic molecules this equation gives rather accurate values of the energy
levels.
The first term of (8.189) represents the harmonic oscillator approximation, the
second is the correction for the anharmonicity due to the Morse function. The third
and the fourth terms describe the rotational part of the energy. The fifth term takes the
interaction of vibration and rotation into account. If still greater accuracy is desired,
a term proportional to (v + 1/2)
3
or even higher powers may be introduced. The
selection rule for J , that is J =±1, is still obeyed in this more complicated model.
The vibrational transitions, however, are not restricted to v =±1 but may also
differ by larger integral amounts. The transitions due to v =±2, v =±3,...
are very weak. As a matter of terminology, transitions for which v =±1 are
known as the fundamental transitions, v =±2 as the first overtone transition or
second harmonic, v =±3 as the second overtone or third harmonics and so on.
Now we discuss an energy level diagram of the diatomic molecule on the assump-
tion that the molecular motion can be approximated as a harmonic oscillator and a
rigid rotator. First we introduce the definition
˜ν
0
= ˜ν
e
(v
− v
) − x
e
˜ν
e
v
+
1
2
2
−
v
+
1
2
2
, v
>v
(8.191)
describing the vibrational energy difference due to the transition v
to v
with
v
>v
. We consider an absorption or emission process between levels having
quantum numbers v
and J
and v
and J
where v
and v
have fixed values. For
J
− J
= 1wefind
˜ν
R
= ˜ν
0
+ 2(J + 1)B
e
(8.192)
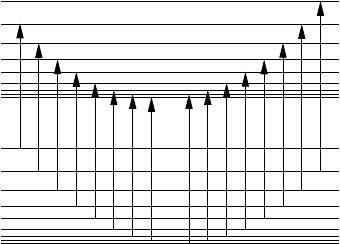
316 Absorption by gases
1234567812345678
2
4
6
8
2
4
6
8
P branch R branch
J
′
v′
v′′
J′′
Fig. 8.10 Schematic representation of the first few P and R transitions of the
vibration–rotation spectrum (rigid rotator and harmonic oscillator approximation)
of a diatomic molecule. After Houghton and Smith (1966).
where J
has been replaced by J for simplicity. The final two terms in (8.189)
have been omitted for simplicity. This transition results in the so-called R branch
as shown in Figure 8.10. If the rotational transition is J
− J
=−1 then we find
˜ν
P
= ˜ν
0
− 2JB
e
(8.193)
describing the P branch.
The fine structure consists of nearly equally spaced lines on each side of the band
center where a line is missing since J = 0. The line spacing has been exaggerated
compared with the spacing of the vibrational levels.
In a very few molecules transitions corresponding to J = 0 are also allowed
giving a group of lines which is called the Q branch. When discussing rotation
of the molecule we have implicitly assumed that there is no angular momentum
about the internuclear axis. It is possible, however, that the electrons surrounding
the nucleus possess angular momentum about this axis resulting in the selection
rule J = 0 so that the Q branch occurs. Since all lines with J = 0 are located
at nearly the same frequency, a strong line is produced at the center of the band.
For additional details see, for example, Houghton and Smith (1966) and Herzberg
(1964a,b).
8.5 Matrix elements, selection rules and line intensities
Without derivations we have previously given the selection rules for the one-
dimensional harmonic oscillator and the rigid rotator. We will now show in which
way these may be obtained.
8.5 Matrix elements, selection rules and line intensities 317
8.5.1 The harmonic oscillator
In the harmonic oscillator approximation the dipole moment varies linearly with
the internuclear distance
M = M
0
+ M
1
(r − r
e
) = M
0
+ M
1
x = M
0
+
M
1
√
β
ξ (8.194)
Here, M
0
is the dipole moment in equilibrium position while x = r − r
e
is the
change of the internuclear distance. The quantity M
1
is the rate of change of the
dipole moment with internuclear distance and ξ =
√
βx. The defining relation
(8.105) for the matrix element is rewritten as
R(v
,v
) = M
0
∞
−∞
ψ
0∗
v
(x)ψ
0
v
(x)dx + M
1
∞
−∞
xψ
0∗
v
(x)ψ
0
v
(x) dx (8.195)
now using the vibrational quantum numbers (v
,v
). From (8.145) we repeat the
complete time-independent one-dimensional harmonic oscillator wave function
ψ
v
(ξ) = N
v
H
v
(ξ)exp
−
ξ
2
2
with N
v
=
%
β
π
1
2
v
v!
1/2
(8.196)
This wave function will be introduced into (8.195) in place of the unperturbed wave
functions. These form a complete orthonormal set. Thus we find
R(v
,v
) = M
0
N
v
N
v
∞
−∞
exp(−ξ
2
)H
v
(ξ)H
v
(ξ)
dξ
√
β
+M
1
N
v
N
v
√
β
∞
−∞
ξ exp(−ξ
2
)H
v
(ξ)H
v
(ξ)
dξ
√
β
(8.197)
Due to the orthogonality relations
∞
−∞
ψ
0∗
v
ψ
0
v
dx = δ
v
,v
(8.198)
the first integral vanishes if v
= v
. In order to evaluate the second integral we
introduce the recursion formula for the Hermite polynomials as given by
ξ H
v
(ξ) = v H
v−1
(ξ) +
1
2
H
v+1
(ξ) (8.199)
Due to the orthogonality of the wave functions we immediately find the selection
rules
v
= v
+ 1,v
= v
− 1, or v
− v
= v =±1
(8.200)
Details of the calculations are left to the exercises.

318 Absorption by gases
We are now ready to calculate the matrix elements for the two transitions v =
±1. We recall from (8.126) that the line intensity is proportional to the square of
the matrix elements. For the one-dimensional harmonic oscillator they are given by
the following two equations
|R(v
,v
)|
2
= M
2
1
v
+ 1
2β
for v =+1
v
2β
for v =−1
(8.201)
More complicated problems do not have an exact solution and approximate methods
must be used. By considering, for example, the harmonic oscillator wave functions
as the unperturbed functions it is possible to tackle the anharmonic oscillator as a
perturbation problem. We are not going to discuss the procedure which is explained
in textbooks on quantum mechanics.
8.5.2 The rigid rotator
For rotational transitions the matrix element may be expressed in the form
R(J
, M
, J
, M
) =
ψ
0∗
J
,M
Mψ
0
J
,M
dτ (8.202)
where J
, M
, J
, M
are the rotational and magnetic quantum numbers of the
upper and lower states. The Cartesian components of the dipole moment in the x,
y and z directions are given by
M
x
=
¯
M sin θ cos ϕ, M
y
=
¯
M sin θ sin ϕ, M
z
=
¯
M cos θ (8.203)
so that the component matrix elements can be written as follows
(a) R
x
(J
, M
, J
, M
) =
¯
M
2π
0
π
0
ψ
0∗
J
,M
ψ
0
J
,M
sin θ cos ϕ sin θ dθ dϕ
(b) R
y
(J
, M
, J
, M
) =
¯
M
2π
0
π
0
ψ
0∗
J
,M
ψ
0
J
,M
sin θ sin ϕ sin θ dθ dϕ
(c) R
z
(J
, M
, J
, M
) =
¯
M
2π
0
π
0
ψ
0∗
J
,M
ψ
0
J
,M
cos θ sin θ dθ dϕ
(8.204)
We recognize immediately that R
x
, R
y
, R
z
differ from zero, that is emission or
absorption by the rotator can occur only when the dipole moment
¯
M is different
from zero.
8.5 Matrix elements, selection rules and line intensities 319
As an example, we will now consider (8.204c) in some detail by substituting the
complete time-independent rigid rotator wave function. Using (8.183) we obtain
R
z
(J
, M
, J
, M
) =
¯
M
N
R
N
R
2π
π
0
P
|M
|
J
(cos θ ) cos θ P
|M
|
J
(cos θ ) sin θdθ
×
2π
0
e
−i(M
−M
)ϕ
dϕ (8.205)
where N
R
and N
R
are the normalization factors of the two states described by the
first integral. The second integral in (8.205) is zero unless M
= M
= M and the
integral is 2π. To evaluate the first integral we employ the recursion formula for
the associated Legendre polynomials
cos θ P
|M|
J
(cos θ ) =
J +|M|
2J + 1
P
|M|
J −1
(cos θ ) +
J −|M|+1
2J + 1
P
|M|
J +1
(cos θ ) (8.206)
and obtain the following equation
R
z
(J
, M
, J
, M
) =
¯
MN
R
N
R
J
+|M|
2J
+ 1
π
0
P
|M|
J
P
|M|
J
−1
sin θ dθ
+
J
−|M|+1
2J
+ 1
π
0
P
|M|
J
P
|M|
J
+1
sin θ dθ
(8.207)
Now we recognize immediately that the matrix elements R
z
(J
, M, J
, M)
vanish unless
J
− J
=−1, J
− J
=+1, or J =±1 (8.208)
and at the same time M
= M
= M or M = 0. Omitting details, for the remain-
ing directions we find the selection rules M =±1,J =±1 which show that
the selection rules for J are the same for the light polarized in each direction.
In order to obtain the line intensity we must calculate the square of the matrix
elements. If J
= J
+ 1 then the second integral on the right-hand side of (8.207)
is zero and we obtain
R
z
(J
, |M|, J
+ 1, |M|) =
¯
MN
R
N
R
N
R
N
R
J
+ 1 +|M|
2(J
+ 1) + 1
π
0
P
|M|
J
P
|M|
J
sin θ dθ
=
¯
M
N
R
N
R
J
+ 1 +|M|
2(J
+ 1) + 1
(8.209)
=
¯
M
&
(J
+ 1 −|M|)(J
+ 1 +|M|)
(2J
+ 1)(2J
+ 3)
320 Absorption by gases
For simplicity we replace J
by J and finally obtain
R
z
(J, |M|, J + 1, |M|) =
¯
M
&
(J + 1 −|M|)(J + 1 +|M|)
(2J + 1)(2J + 3)
(8.210)
Setting J
= J
− 1, the first integral is zero and we obtain the expression
R
z
(J, |M|, J − 1, |M|) =
¯
M
&
(J +|M|)(J −|M|)
(2J + 1)(2J − 1)
(8.211)
By using proper recursion relations R
x
and R
y
can be found analogously. The
results are given, for example, in Penner (1959). The square of the total matrix
element may be evaluated by summing over the components and over all allowed
values of M
and M
as stated in
M
,M
|R(J
, M
, J
, M
)|
2
=
¯
M
2
(J
+ 1) for J =+1
¯
M
2
J
for J =−1
(8.212)
For the pure rotation spectrum, transitions in absorption always result from
J =+1.
Equations (8.201) and (8.212) referring to the harmonic oscillator and the rigid
rotator can be superimposed. We consider the case that absorption takes place from
the vibrational state v
. Thus for the combined transition (rotator plus oscillator)
we may write
M
,M
|R(v
, J
, M
,v
+ 1, J
, M
)|
2
= M
2
1
(v
+ 1)
2β
(J
+ 1) R branch
J
P branch
(8.213)
For additional details see, for example, Penner’s (1959) description of the matrix
elements for the rotational lines belonging to the rotation–vibration bands.
8.6 Influence of thermal distribution of quantum states on line intensities
Now we return to equation (8.113) which requires information on the population
of the energy levels. The population N
i
of a level having an energy E
i
above the
ground state of the molecule is given by the Maxwell–Boltzmann distribution
N
i
=
g
i
Z
N exp
−
E
i
kT
with Z =
i
g
i
exp
−
E
i
kT
(8.214)

8.6 Distribution of quantum states and line intensities 321
Here, N is the total number of molecules and Z the sum over all states usually called
the partition function. The quantity g
i
is the statistical weight of the energy level
E
i
. Herzberg (1964a) provides a table showing that for most diatomic molecules
at atmospheric temperatures the number of molecules in the first vibrational level
is very small compared to the ground state. Hence practically all transitions in
absorption observed in the infrared spectrum have v
= 0 as the initial state. For
vibrational transitions it is often possible to ignore the ratio N
n
/g
n
in comparison
to N
m
/g
m
in (8.126).
From (8.181) follows that the number of molecules N
J
in the rotational level J
of the lowest vibrational state is given by
N
J
=
2J + 1
Z
R
N exp
−
BJ(J + 1)hc
kT
(8.215)
where 2J + 1 is the statistical weight, B = h/(8π
2
Ic) is the so-called rotational
constant and
Z
R
=
J
(2J + 1) exp
−
BJ(J + 1)hc
kT
(8.216)
is the rotational partition function. The quantity E
i
was obtained from (8.181)
which was divided by hc so that E
i
is expressed in cm
−1
. Since B is usu-
ally quite small, for sufficiently large T , Z
R
may be expressed by an integral
which can be evaluated analytically. Setting x = J (J + 1) we find the approximate
expression
Z
R
≈
∞
0
exp
−
Bhcx
kT
dx =
kT
Bhc
(8.217)
resulting for N
J
in the simplified expression
N
J
≈
NhcB
kT
(2J + 1) exp
−
BJ(J + 1)hc
kT
(8.218)
We may now substitute (8.215) into (8.126), remembering that g
n
= 2J
+ 1,
and find for the line intensity the expression
S ≈
2π
2
ν N
3hε
0
cZ
R
i
k
|R(m
i
, n
k
)|
2
exp
−
BJ
(J
+ 1)hc
kT
(8.219)
which is identical with the corresponding expression given by Herzberg (1964b).
Observing that Z
R
is approximately given by (8.217) and by replacing the double
322 Absorption by gases
123456789101112
1.0
2.0
3.0
4.0
J
ψ(J)
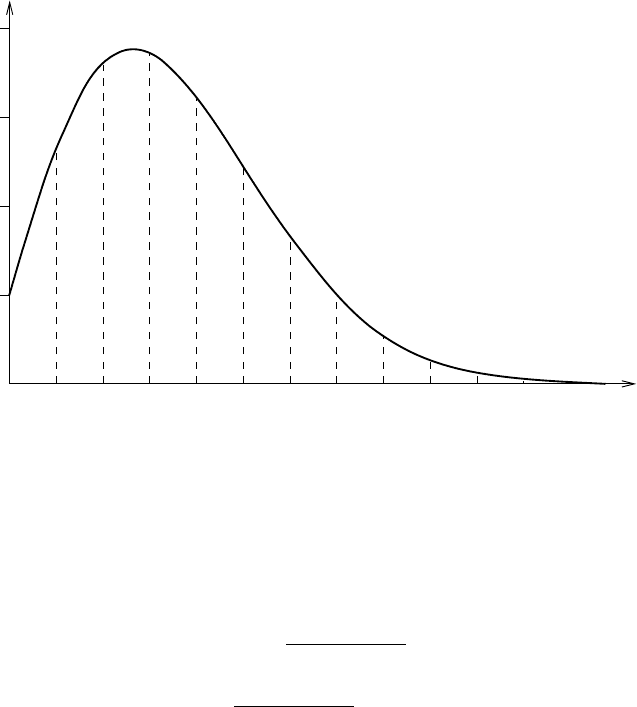
Fig. 8.11 Schematic picture of the thermal distribution of the rotational lev-
els of the HCl molecule in the vibrational ground state, T = 300 K. ψ(J ) =
(2J + 1) exp[−BJ ( J + 1)hc/(kT)]. After Herzberg (1964a) Spectra of Diatomic
Molecules.
sum expression in (8.219) by (8.213) we find that the part of S depending on J
is
given by
S
J
=
(J + 1) exp
−
BJ(J + 1)hc
kT
R branch
J exp
−
BJ(J + 1)hc
kT
P branch
(8.220)
where we have replaced J
by J for brevity. Inspection shows that S
J
varies with
J almost in the same manner as the population density N
J
defined by equation
(8.215). For the HCl molecule this variation is depicted in Figure 8.11. Since the
factor (2J + 1) varies linearly with J , the number of molecules in the different
rotational levels does not from the beginning decrease with the rotational quantum
number but goes through a maximum.
8.7 Rotational energy levels of polyatomic molecules
Let us consider the rotation of a polyatomic molecule assuming that it is a rigid struc-
ture. By expanding the angular momentum vector (8.12) we find for the vector com-
ponents J
x
, J
y
, J
z
expressions containing terms of the type I
x
=
i
m
i
(y
2
i
+ z
2
i
)
8.7 Rotational energy levels of polyatomic molecules 323
H
H
H
H
H
H
I
A
I
B
I
C
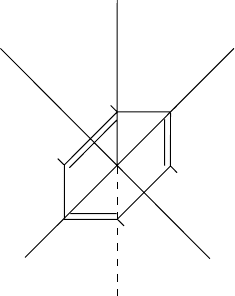
Fig. 8.12 Example of a symmetric top molecule. After Barrow (1962).
and P
xy
=
i
m
i
x
i
y
i
. The I
x
, I
y
, I
z
are the moments of inertia about the coordinate
axes. The coordinate axes are called principal axes for the body at the origin if all
the products of inertia P
xy
, P
yz
, P
zx
vanish. If the body (molecule) has symmetry,
the direction of one or more of the principal axes going through the center of mass
can be found, since axes of symmetry are always principal axes and a plane of
symmetry is perpendicular to a principal axis.
The number of rotational quantum numbers which are needed to specify a given
rotational state depends on the particular molecular geometry. Only a very brief
and incomplete description can be reviewed here. A detailed account is given in
Infrared and Raman Spectra by Herzberg (1964b).
We will now briefly describe the pure rotation of polyatomic molecules, i.e. we
consider non-vibrating molecules in a fixed electronic state. There are four basic
types which are distinguished according to their three principal moments of inertia
which are denoted by I
A
, I
B
, I
C
. We will give a few atmospheric examples which
are taken from Goody (1964a).
(i) Linear molecules (CO
2
,N
2
O, O
2
,N
2
, CO): I
A
= 0, I
B
= I
C
= 0
(ii) Symmetric top molecules (no common atmospheric gases): I
A
= 0, I
B
= I
C
= 0
(iii) Spherical top molecules (CH
4
): I
A
= I
B
= I
C
(iv) Asymmetric top molecules (H
2
O, O
3
): I
A
= I
B
= I
C
Of the listed molecules only H
2
O has an important pure rotation spectrum. The
symmetry property is best demonstrated in case of the benzene molecule which is
a symmetric top molecule, see Figure 8.12. The unique moment of inertia of the
molecule is usually represented by I
A
while the two equal moments of inertia are
I
B
and I
C
.
324 Absorption by gases
2(h/2π)
1(h/2π)
−1(h/2π)
−2(h/2π)
0(h/2π)
2(2 + 1)(h
/
2
π
)
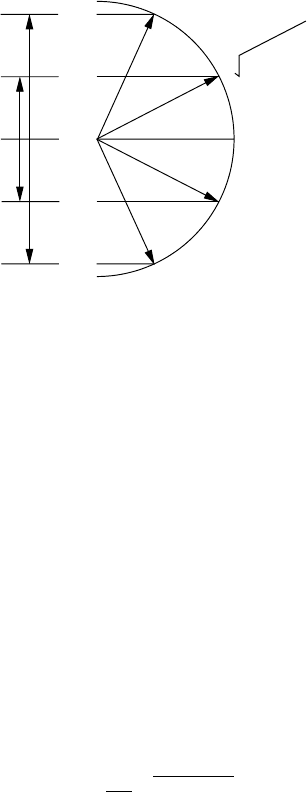
Fig. 8.13 Total and component angular momentum vectors for J = 2. The applied
field reveals 2J + 1 = 5 components. Left part: Angular momentum component in
direction of an applied field. Right part: angular momentum of rotating molecule.
Illustration of the degeneracy 2J + 1. After Barrow (1962).
8.7.1 Linear molecules
In case of linear molecules and spherical top molecules only one quantum number
J is required to describe the rotational state. For linear molecules the solution of
Schr¨odinger’s equation for rotation is the same as that for the diatomic molecule.
The same selection rules J =±1 are obeyed for dipole transitions. As stated
before, unless the molecule possesses a permanent dipole moment no transitions
are possible as in case of carbon dioxide which is a symmetrical molecule O–C–O.
The N
2
O molecule (N–N–O) possesses a permanent dipole moment so that purely
rotational transitions are allowed.
As we have previously seen, the rotational energy of the diatomic molecule
depends only on the angular momentum quantum number J . The magnitude of the
angular momentum itself is given by
|J|=
h
2π
-
J (J + 1) (8.221)
In addition to J , there exists the quantum number M = 0, ±1,...± J . Thus
a total of 2J + 1 wave functions can be constructed. This is called the 2J + 1
degeneracy of the Jth energy level. If J = 2, for example, M assumes the val-
ues −2, −1, 0, 1, 2 so that five different wave functions can be written down with
the help of (8.183). The quantum numbers M enumerate the possible compo-
nents of the angular momentum J of the rotating molecule in the direction of
an applied (magnetic or electric) field. The resulting angle between J and the
field is not arbitrary, but it is described by the rule that the components in the
direction of the applied field are ±Mh/2π.ForJ = 2 this is demonstrated in
Figure 8.13. The figure implies that the angular momentum vector J is never in
