Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань
Подождите немного. Документ загружается.

Методи врівноваження багатьох виміряних величин
З і
Та
СІЛІ
НІ
а]
Ь]
с]
d]
F\
2]
W
І;
W
4,00
2,00 0,00 0,56
-0,56 6,00
-1,24
4//
И
-1,0000 -0,5000 0,0000
-0,1405 0,1413
-1,4992 0,3100
-I.I!
к\
1.0605 0,7763
0,0000 -0,0258
0,3100
\Ь
4,00 2,00 -2,48
0,30 5,82 4,43
Ю.
п
-1,0000
0,0000 -0,2810 0,2827 -2,9983 0,6200
-2,3
[М
3,0000 2,0000 -2,7585 0,5761
2,8176 5,0500
7,K<
е2
-1,0000 -0,6667 0,9195 -0,1920
-0,9392
-1,6833
-2,h
к2
-1,5525 -0,0379 0,1687
-1,6833
\с
4,00 -0,50
-0,09
5,41
2,97
8..
П
0,0000 0,0000 0,0000
0,0000 0,0000
().()(
ПІ
-1,3333 1,8390 -0,3841
-1,8784
-3,3667
-5,2
\с2 2,ті
1,3358 -0,4720
3,5304
-0,3967
З,І:
еЗ
-1,0000
-0,5009
0,1770 -1,3239 0,1488
-I.I
кЗ
0,0568 -0,0919
0,1448
\d 15,65
1,54 14,77 -7,29 7,.
П
-0,0790
0,0794 -0,8426 0,1742
-0,6
ПІ
-2,5365 0,5297 2,5908 4,6435
7,2
П2
-0,6691 0,2364 -1,7685 0,1987
-1,5
\d3
12,3655 2,3860
14,7515
-2,2687
12/
е4
-1,0000 -0,1930
-1,1930
0,1835
-1,(
к4
0,1835
1,47 2,65
0,1835
W
-0,0799 0,8476
П
-0,1106
-0,5411
ПІ
-0,0836 0,6249
П2
-0,4604 -2,8464
[F4
1
PF
0,7395
0,7395
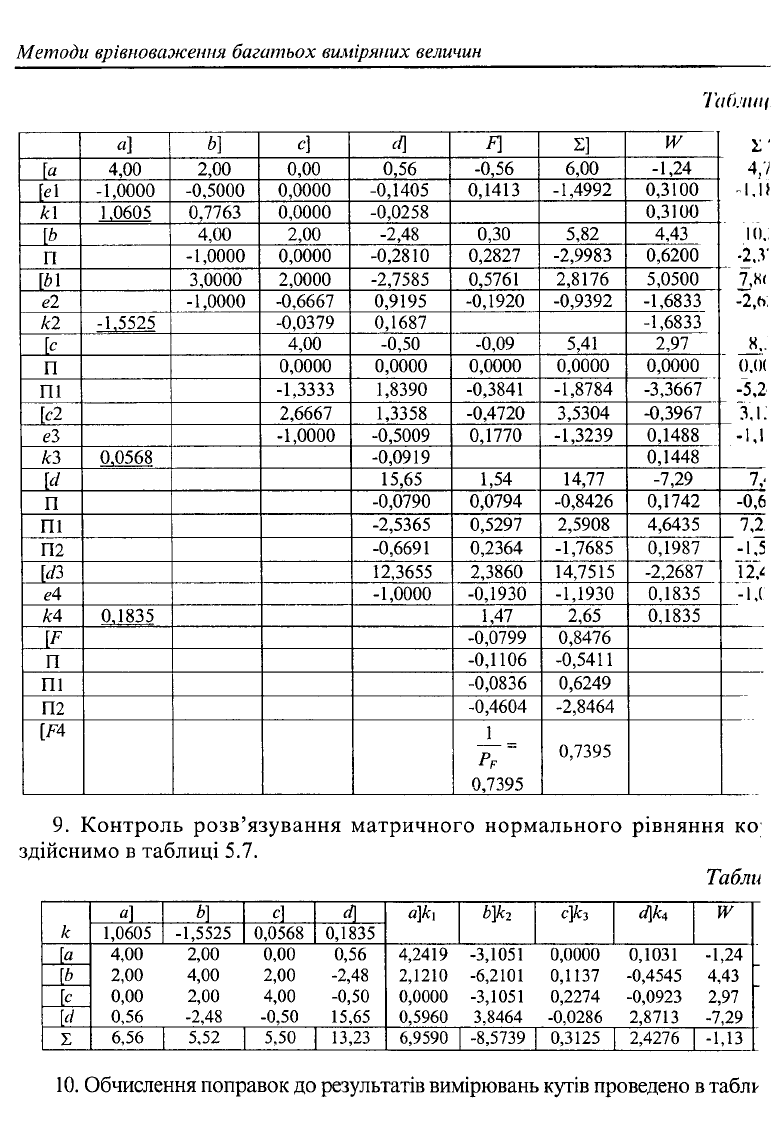
9.
Контроль розв'язування матричного нормального рівняння
ко
здійснимо
в
таблиці
5.7.
Табли
«1
b\
c]
d\
a]k\
b]k
2
Фз
d\k
A
W
k
1,0605 -1,5525 0,0568 0,1835
f«
4,00 2,00 0,00 0,56
4,2419 -3,1051 0,0000 0,1031
-1,24
\b
2,00 4,00 2,00 -2,48
2,1210
-6,2101 0,1137 -0,4545
4,43
\c 0,00 2,00 4,00 -0,50
0,0000
-3,1051
0,2274
-0,0923
2,97
\d 0,56
-2,48 -0,50
15,65
0,5960 3,8464 -0,0286
2,8713
-7,29
S
6,56 5,52 5,50
13,23
6,9590 -8,5739 0,3125
2,4276
-1,13
10.
Обчислення поправок
до
результатів вимірювань кутів проведено
в
таблг
354
Розділ
V
Таблиця
5.8
№
а b
с d V V?
кута
1,0605 -1,5525
0,0568 0,1835
1 1
0 0 2,45
1,509
2,2777
2 1 0
0 -0,66
0,940 0,8841
3 1 1
0 0,38
-0,422 0,1782
4
1 1 0 -1,61
-0,787 0,6199
5
0
1 1 0,76
-1,355 1,8371
6 0 1 1 -2,01
-1,865 3,4786
7
0
0 1
1,26
0,289 0,0833
8 0 0 1 -0,52
-0,038 0,0015
W
-1,24 4,43
2, 97 -7,29 [v
2
] =
9,3605
kW
-1,3150 -6,8777
0,1688 -1,3366
-fv
2
l
=
-9,3605
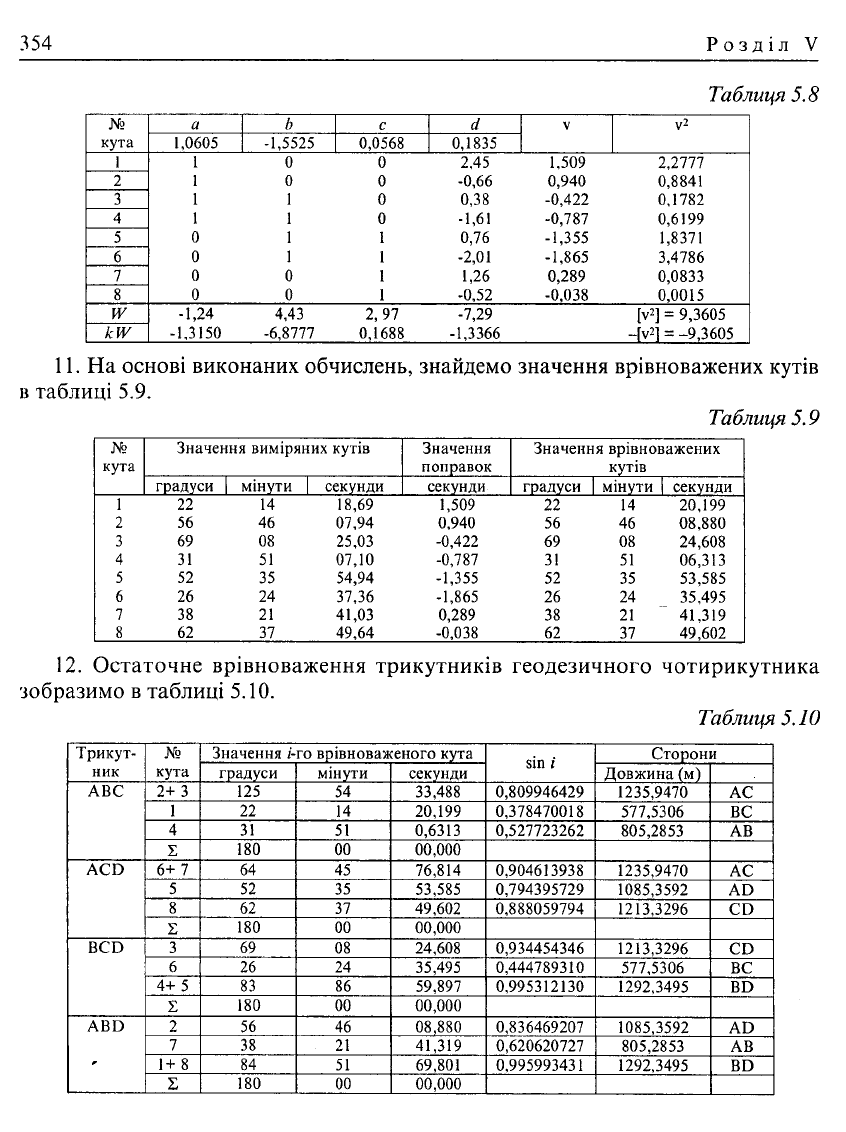
11. На
основі виконаних обчислень, знайдемо значення врівноважених кутів
в
таблиці
5.9.
Таблиця
5.9
№
Значення виміряних кутів Значення
Значення врівноважених
кута
поправок кутів
градуси мінути секунди
секунди градуси мінути
секунди
1 22 14 18,69
1,509 22 14
20,199
2 56
46
07,94 0,940
56
46
08,880
3 69 08
25,03 -0,422
69 08
24,608
4
31 51 07,10
-0,787
31
51
06,313
5 52
35
54,94
-1,355
52
35
53,585
6
26
24
37,36 -1,865
26 24
35,495
7 38 21
41,03
0,289
38 21
41,319
8 62
37
49,64 -0,038
62
37
49,602
12.
Остаточне врівноваження трикутників геодезичного чотирикутника
зобразимо
в
таблиці
5.10.
Таблиця
5.10
Трикут-
ник
№
кута
Значення
/'-го
врівноваженого кута
sin і
Сторони
Трикут-
ник
№
кута
градуси мінути
секунди
sin і
Довжина
(м)
ABC 2+ 3 125 54
33,488 0,809946429
1235,9470
АС
ABC
1 22 14
20,199
0,378470018 577,5306
ВС
ABC
4
31 51
0,6313
0,527723262
805,2853
АВ
ABC
£
180 00
00,000
ACD
6+ 7 64
45
76,814
0,904613938 1235,9470
АС
ACD
5 52 35
53,585 0,794395729
1085,3592
AD
ACD
8
62 37
49,602 0,888059794
1213,3296
CD
ACD
180 00
00,000
BCD 3
69 08
24,608 0,934454346
1213,3296
CD
BCD
6 26 24
35,495 0,444789310
577,5306
ВС
BCD
4+ 5
83
86
59,897 0,995312130
1292,3495
BD
BCD
£
180
00
00,000
ABD
2 56
46
08,880
0,836469207
1085,3592
AD
ABD
7
38 21
41,319 0,620620727
805,2853
АВ
ABD
1+ 8 84
51
69,801
0,995993431
1292,3495
BD
ABD
2
180
00
00,000
Методи врівноваження багатьох виміряних величин З і
13. Виконаємо оцінку точності отриманих результатів врівноваження. Для ці
а) обчислимо середню квадратичну похибку одиниці ваги
б) знайдемо середню квадратичну похибку довжини сторони BD
m
BD
=±\BD\^l^ = ±1292,3495V0J395 -±0,0082(м).
р \ P
F
206265
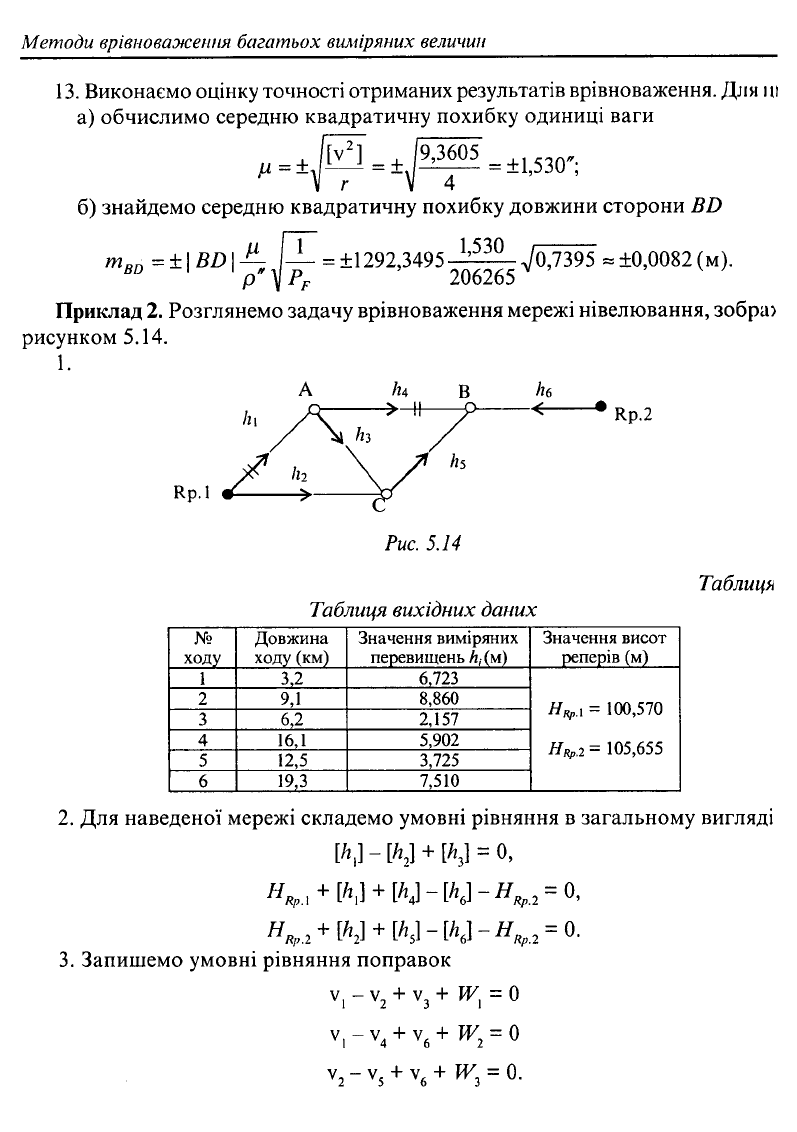
Приклад 2. Розглянемо задачу врівноваження мережі нівелювання, зобра>
рисунком 5.14.
1.
Rp.l
/н В h
6
< * Rp.2
h
' hi
Рис.
5.14
Таблиця вихідних даних
Таблиця
№
ходу
Довжина
ходу (км)
Значення виміряних
перевищень А/( м)
Значення висот
реперів (м)
1
3.2 6,723
2
9,1
8,860
Я*,
і
= 100,570
3 6,2 2,157
Я*,
і
= 100,570
4 16,1
5,902
Я*.2 = 105,655
5
12,5 3,725
Я*.2 = 105,655
6 19,3
7,510
2. Для наведеної мережі складемо умовні рівняння в загальному вигляді
[А,]-[/у+ [й
3
] = 0,
H^ + W + W-W-H^o,
H
R
,
2
+
[h
2
]
+ [h
s
]-[h
6
]-H
Rp2
= 0.
3. Запишемо умовні рівняння поправок
у,-У
2
+ У
3
+Ж, = 0
v,-v
4
+ v
6
+^
2
= 0
v
2
-v
5
+ v
6
+^
3
= 0.

356
Розділ V
4. Обчислимо нев'язки Щ(і = 1,3) в умовних рівняннях поправок
Ж, = (/?,) - (h
2
) + (h
3
) = 6,723 - 8,860 + 2,157 = 0,020 (м);
Ж, = Н^, - Н
Щі2
+ (h) + (/g -
(Л
6
)
= 100,570 -105,655 + 6,723 + 5,902 - 7,510 = 0,030 (м);
Ж
3
= Н^ -H
Rp2
+ (Л
2
) + (h) -
(h
6
)
= 100,570 -105,655 + 8,860 + 3,725 - 7,510 = -0,010 (м);
5. Складаємо вагову функцію. Нею буде висота точки В відносно Н ,
тобто
F= (Л,) + (h
4
).
6. Ваги результатів вимірювань визначаємо так:
РІ =-- = -—0 = 1,6),
d
i
d
i
де
б?.
- відповідні довжини ходів.
7. Побудуємо таблицю 5.12 коефіцієнтів умовних рівнянь поправок та вагової
функції.
\ Таблиця 5.12
№
ходу
а b
с
/
І 1/р а/р Ь/р с/р F/p
s/p
1 1 1 0 1 3 0,32 0,32
0,32 0,00 0,32
0,96
2
-1
0 1 0 0
0,91 -0,91 0,00 0,91 0,00
0,00
3
1
0 0 0 1 0,62
0,62 0,00 0,00
0,00 0,62
4 0 1 0 1
2 1,61 0,00 1,61 0,00
1,61 3,22
5
0 0 1
0 1 1,25 0,00 0,00
1,25 0,00
1,25
6
0 -1 -1
0 -2 1,93 0,00
-1,93 -1,93 0,00
-3,86
2
1 1 1
2
5 0,03 0,00
0,23 1,93 2,19
8.Коефіцієнти нормального матричного рівняння корелат помістимо в
таблицю 5.13.
Таблиця 5.13
Ф1
b/p\
1 c/p]
F/p1
s/p]
f«
1,85 0,32
-0,91 0,32
1,58
\b 3,86 1,93
1,93
8,04
\c
4,09 0,00
5,11
\f
1,93 4,18
\s 18,91
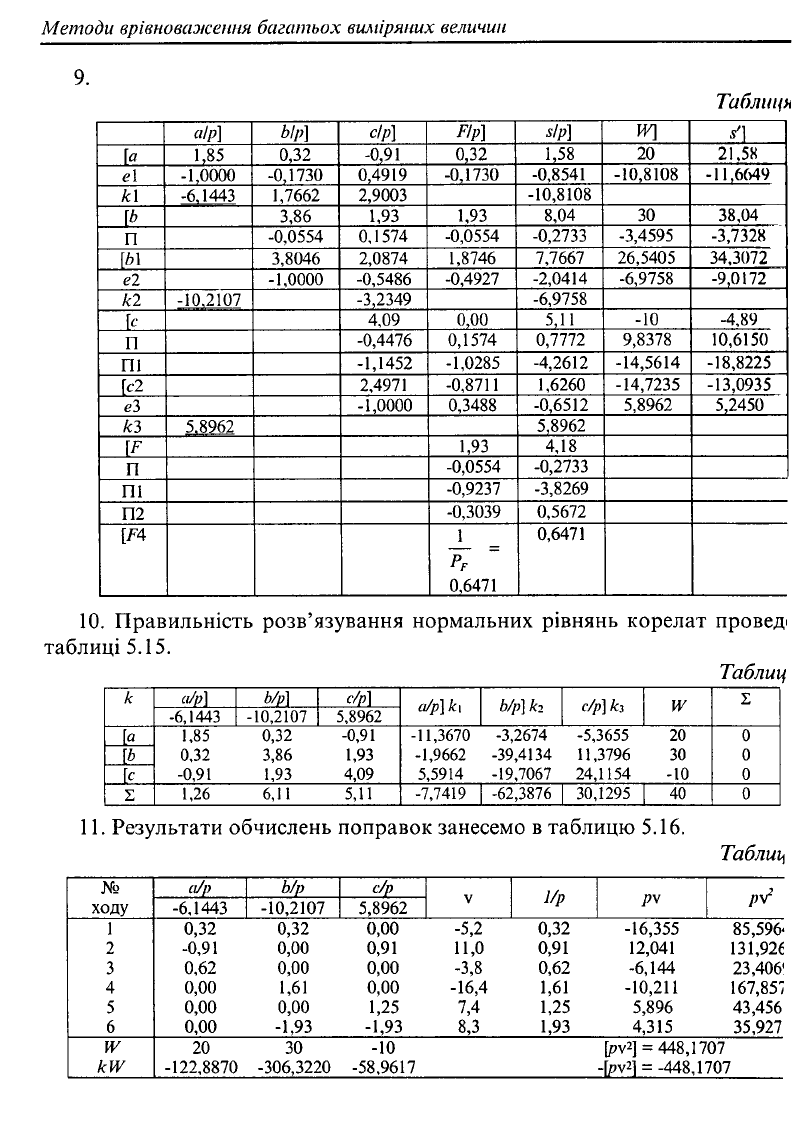
Для розв'язування нормального матричного рівняння корелат, аналогічно,
як і в попередньому прикладі, скористаємося схемою Ґаусса-Дулітля і результати
обчислень запишемо в таблицю 5.14.
Методи врівноваження багатьох виміряних величин
З і
Таблиця
аїр]
ЬІР)
Ф]
Flp]
sip] W]
\а
1,85
0,32
-0,91 0,32
1,58 20
21,58
el
-1,0000
-0,1730 0,4919
-0,1730
-0,8541 -10,8108
-11,6649
кі
-6.1443
1,7662 2,9003
-10,8108
\ь
3,86 1,93
1,93
8,04 30
38,04
п
-0,0554
0,1574 -0,0554 -0,2733
-3,4595 -3,7328
ЇМ
3,8046
2,0874 1,8746
7,7667 26,5405
34,3072
е2
-1,0000 -0,5486
-0,4927
-2,0414 -6,9758 -9,0172
к2
-10.2107
-3,2349
-6,9758
\с
4,09
0,00
5,11
-10 -4,89
П
-0,4476
0,1574 0,7772
9,8378
10,6150
ПІ
-1,1452
-1,0285 -4,2612
-14,5614
-18,8225
\с2
2,4971
-0,8711 1,6260
-14,7235
-13,0935
еЗ
-1,0000 0,3488
-0,6512 5,8962 5,2450
кЗ
5.8962
5,8962
\F
1,93
4,18
П
-0,0554 -0,2733
ПІ
-0,9237 -3,8269
П2
-0,3039
0,5672
[F4
1
Pf
0,6471
0,6471
10.
Правильність розв'язування нормальних рівнянь корелат проведі
таблиці
5.15.
Таблиц
k
afp\
b/p] c/p]
a/p]k\
b/p]
кг
c/p]
кг W
I
-6,1443
-10,2107 5,8962
a/p]k\
b/p]
кг
c/p]
кг W
[«
1,85
0,32 -0,91
-11,3670
-3,2674
-5,3655
20
0
f ь
0,32
3,86
1,93
-1,9662
-39,4134
11,3796
30 0
\<=
-0,91
1,93 4,09
5,5914
-19,7067
24,1154
-10 0
s
1,26 6,11
5,11
-7,7419
-62,3876 30,1295
40 0
11.
Результати обчислень поправок занесемо
в
таблицю
5.16.
Таблиц
№
ci/p b/p
c/p
I/n
py
ходу
-6,1443 -10,2107
5,8962
1/p
py
pyr
1 0,32 0,32 0,00
-5,2 0,32
-16,355
85,596-
2
-0,91
0,00 0,91 11,0 0,91
12,041 131,926
3
0,62 0,00 0,00 -3,8 0,62
-6,144
23,406'
4 0,00
1,61
0,00 -16,4
1,61
-10,211
167,857
5 0,00 0,00 1,25 7,4 1,25
5,896 43,456
6 0,00 -1,93 -1,93 8,3 1,93 4,315
35,927
W
20 30 -10
\pw
2
]- 448,1707
kW
-122,8870 -306,3220 -58,9617
-И
2
] =
-448,1707

358 Розділ V
12. Врівноважені перевищення та визначені висоти реперів А, В, С подамо
таблицею 5.17.
Таблиця 5.17
№
ходу
Значення перевищень (м)
Значення висот реперів (м)
№
ходу
Виміряні Поправки
Врівноважені
Репери Обчислення
Висота
1 6,723 -0,0052 6,7178
Rp. і
- 100,5700
2
8,860 0,0110
8,8710
Rp. 2
-
105,6550
3
2,157 -0,0038 2,1532 Значення висот точок (м)
4
5,902 -0,0164
5,8856 А
Al 107,2878
5 3,725
0,0074
3,7324
В
Я ^
2+
h
113,1733
6
7,510
0,0083 7,5183 С
Я
Яр
,+
h
2
109,4410
13. Виконаємо оцінку точності врівноважених перевищень та отриманих висот
реперів, для чого
а) обчислимо середню квадратичну похибку одиниці ваги
б) визначимо середню квадратичну похибку функції врівноважених величин
= ±/л ^ = ±12,8^/0,6471 = ±10,3 (мм);
в) знайдемо середню квадратичну похибку на один кілометр ходу
т = ±-^ = ±Ц£ = ± 4,0 (мм).
л/Я л/10
§ 5.13. Умовні рівняння поправок у геодезичних мережах при
використанні параметричного методу врівноваження
1. Розглянемо мережу, зображену рисунком 5.15, у якій виміряно шість кутів

Методи врівноваження багатьох виміряних величин
З і
За параметри можна вибрати кути а.(/ = 1,3). Тоді рівняння поправок
загальному вигляді можна записати так:
t. = [а], / = 1,3,
+
*2
= [«J.
t
2
+ t
3
= [a
5
], (5.123)
І'/=[а
6
]-
/=і
де /.(/ = 1,3) - параметри.
Введемо поправки г
і
(і = 1,3) до найближених значень параметрів tf (/ = 1,3) та
до виміряних кутів а. (/ = 1,6) мережі. У результаті система рівнянь (5.123)набу,
вигляду
+т, =а,- +v,.,/ = 1,3,
+т, + /
2
= (a
4
) + v
4
,
t
2
+т
2
+
/
3
°
+ т
3
=(a
5
) + v
5
,
£(/" +т,) = (а
6
) + у
6
,
/=і
або остаточно отримаємо лінійні рівняння поправок
т, +/,• =v
(
-,/ = l,3,
Т, +Т 2 +/
4
=v
4
,
т
2
+ т
3
+/
5
= v
5
,
+/
6 =
v
6,
(=1
де /. = /° -(а,.)(/ = й),/
4
=/,° +/
2
° -(«
4
),/
5
=/
2
° + /
3
° -(a
5
),/
6
=hf -(a
6
).
і=і
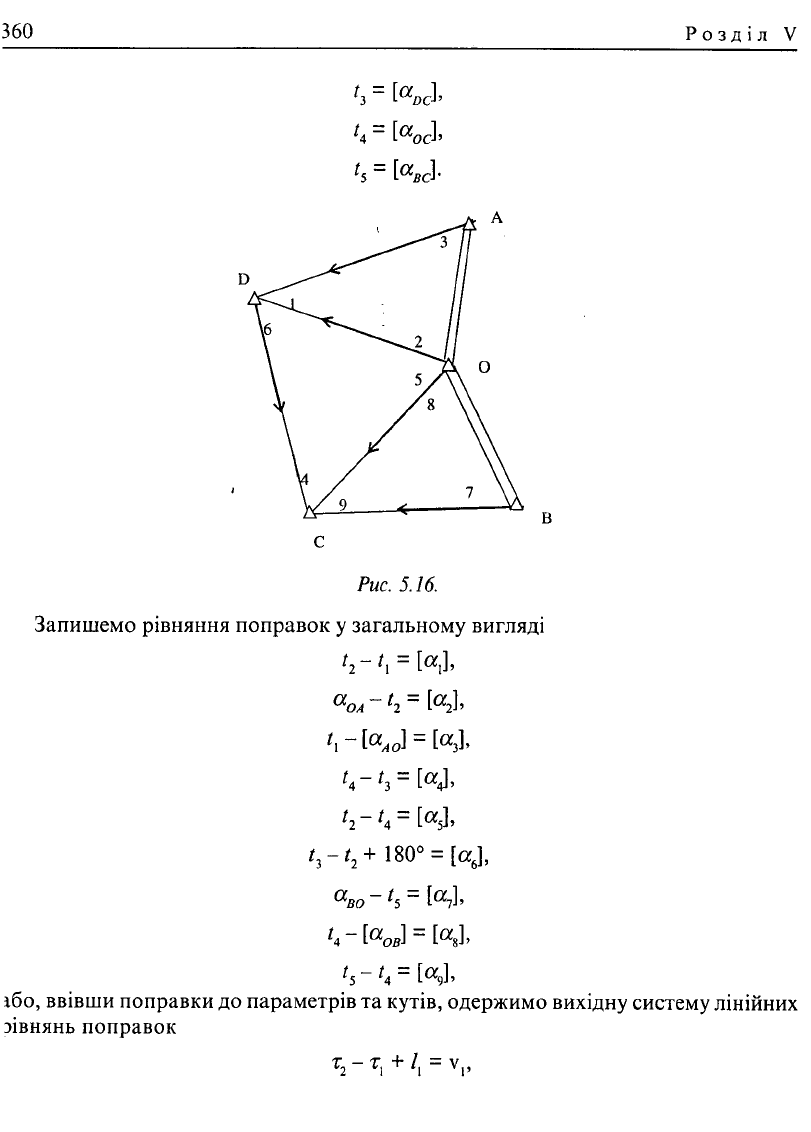
2. Побудуємо систему лінійних рівнянь поправок для мережі, поданої рисунк<
5.16 у якій є виміряними дев'ять кутів і два вихідні дирекційні кути сторін OA та О
У наведеній мережі параметрами будуть дирекційні кути сторін AD, OD, D
ОС і ВС, тобто
= [«J>
t
2
= [«О j'
360
Розділ V
>3
=
KcJ>
'4 = [«осі»
'$ = [««:]•
С
/V. 5.16.
Запишемо рівняння поправок у загальному вигляді
h - = [а,],
- [aj = [од,
'
4
-'з = [aj>
'2-'
4
= [aj.
/
3
-ґ
2
+ 180° = [«
6
]
3
'
4
-[«
0
J = K].
'5 " '4
=
[«J'
160, ввівши поправки до параметрів та кутів, одержимо вихідну систему лінійних
зівнянь поправок
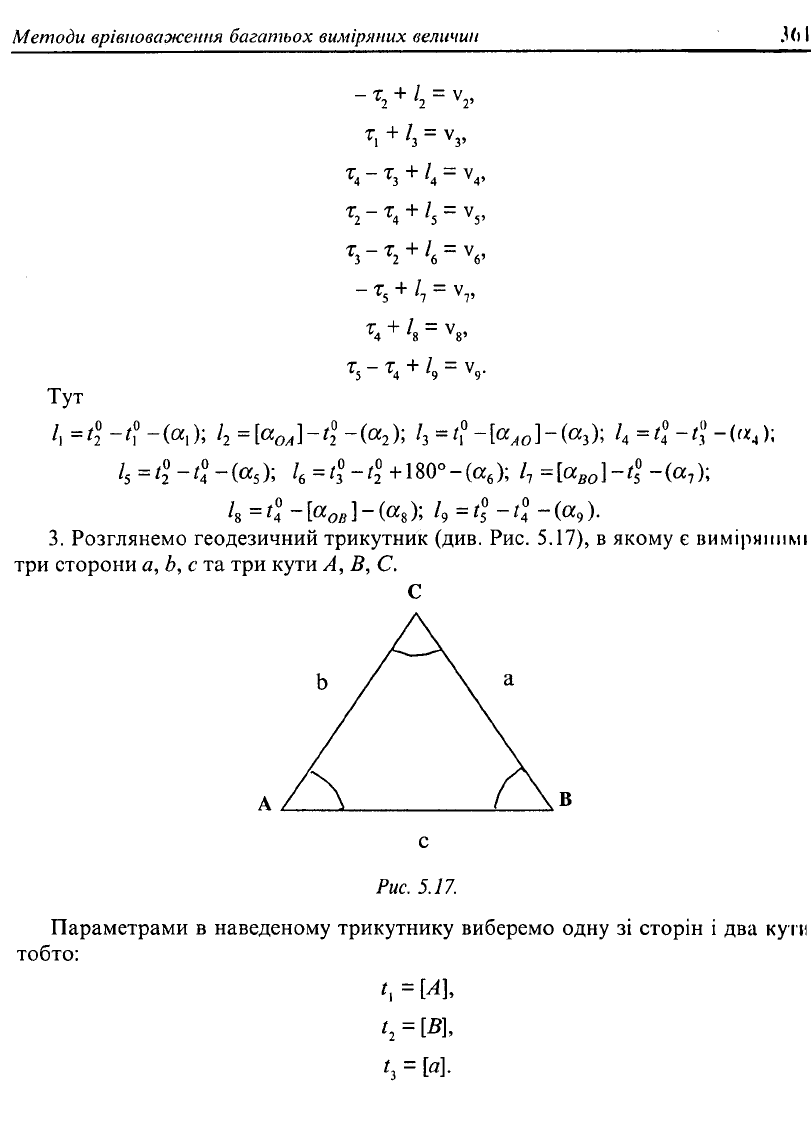
Методи врівноваження багатьох виміряних величин З і
- Т
2
+ /
2
= V
2
,
т, + /3 = V,,
*4-
T
3
+ /
4
= V
4>
T
2-
T
4
+ /
5
= V
5>
T
3-
T
2
+ /
6
= V
6'
- r
5
+ /
7
= v
7
,
*4
+ h =
V
8'
T
5-
T
4
+ /
9 = V
Тут
/, =
r
2
°
- - (a,); /
2
= [a
OA
]-t°
2
- (a
2
); /
3
= ~[a
AO
]~ (a
3
); /
4
= -
*
3
°
- («
4
);
l
5
=t°
2
-t°
4
-(a
5
)- l
6
=(3 -t
2
+180°-(a
6
); /
7
=[a
B0
]-r
5
° -(a
7
);
4 =
'4
0
- [«ся
]
- («8); h =
(5
~ $ - («9 )•
3. Розглянемо геодезичний трикутник (див. Рис. 5.17), в якому є виміриішмі
три сторони a, b, с та три кути А, В, С.
С
Параметрами в наведеному трикутнику виберемо одну зі сторін і два кути
тобто:
t
2
= [B],
h = [а].

362
Розділ V
Загальний вигляд рівнянь поправок буде таким:
t,=[A],
t
2
= [В],
n-t
x
-t
2
= [C\,
t
3
= [а],
sin и
(5.124)
sm t.
sin(?r
—
r, ~t
2
)
sin
t
x
h =W-
Перші чотири рівняння системи (5.124) є лінійними. Лінеаризуємо два останні
рівняння.
_ sin t
2
Введемо позначення — t
3
= J(t
x
,t
2
,t
3
) і знайдемо часткові похідні функції/
sin?,
за змінними t
v
t
2
, t
3
V
dt
x
sin t
2
cos
t, =—
sin?.
• 5 ч
sm /, sin?,
•hctgt
x
\
3/ _ cos t
2
at
2
sin
3/ _ sin t
2
dt
3
sin
t
x
Використавши формулу Тейлора та обмежившись лінійними членами
розкладу, отримаємо
4
a
S
т,+
т
2
+
3L
dt,
v
J
у
т
3
=
sin t
1
1°
sm t
2 ,0
smt
0 'з ч
sm t;
nctgq +
sin?? COSt, о
+ ^2 • о . \tl+Ti
sin t
x
sin t
2
sm(
2 ,0
sin q t
3
h о ~/o
1
- ctgt
x
z
x
+ ctgt
2
x
2
+ -4-т
3
Де Jo =-—^t
3
.
sm t?
