Юсевич А.И. Расчет химико-технологических систем средствами Mathcad
Подождите немного. Документ загружается.


51
CA
CB
t
tck
Odesolve
CA
CB
t
tck
400
CA
CB
t
tck
Odesolve
CA
CB
t
tck
400
tck 0
tck0t 0
t0CB 0
CB0CA 0
CA0
K F t
tcn tck
2
Gc Cc tck
tcn
K F t
tcn tck
2
V CA
CMA CB
CMB CD0 CMD
G CG
t
d
d
V H t
r2 CA
CB
t
r1 CA
CB
t
V CA
CMA CB
CMB CD0 CMD
G CG
CB
d
d
r1 CA
CB
t
r2 CA
CB
t
CA
d
d
r1 CA
CB
t
r2 CA
CB
t
Given
Решение системы дифференциальных уравнений
покомпонентных материальных и теплового балансов реактора:
tck0 7.098tck0 Find tck0( )
K F t0
tcn tck0
2
Gc Cc tck0 tcn( )
Giventck0 1
Нахождение температуры теплоносителя
на выходе из реактора в начальный момент времени:
52
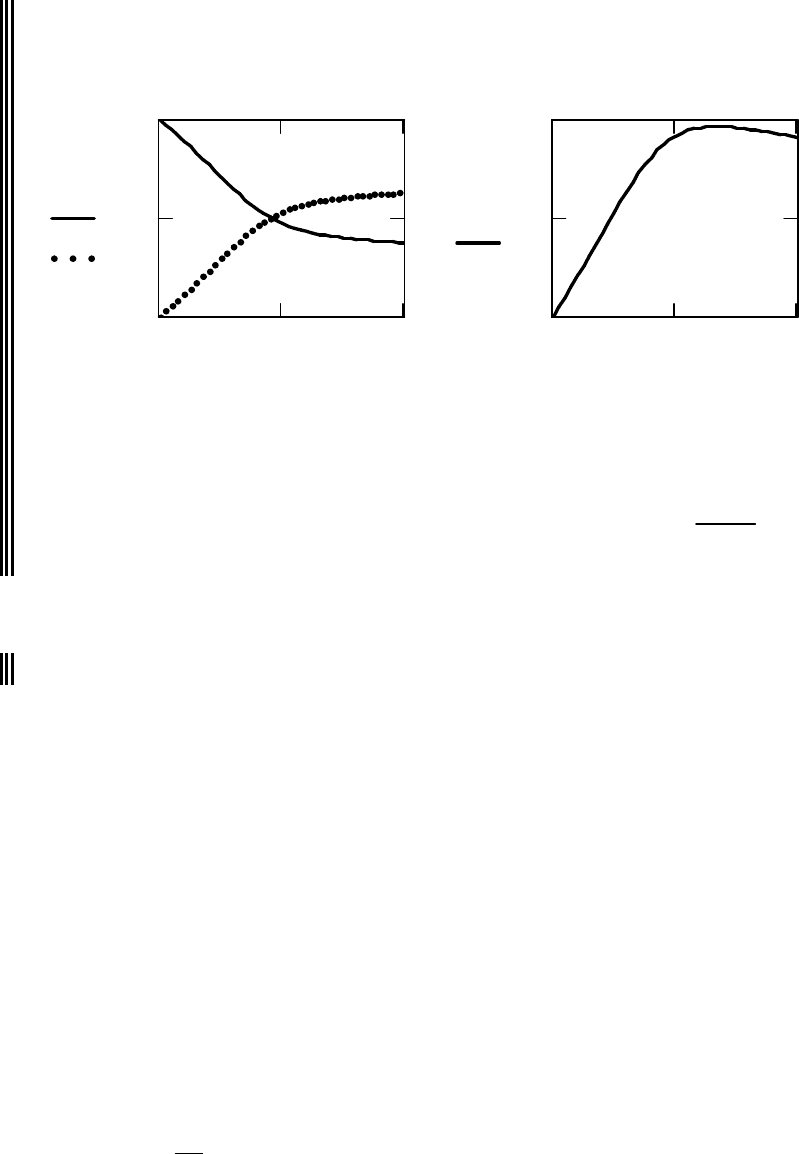
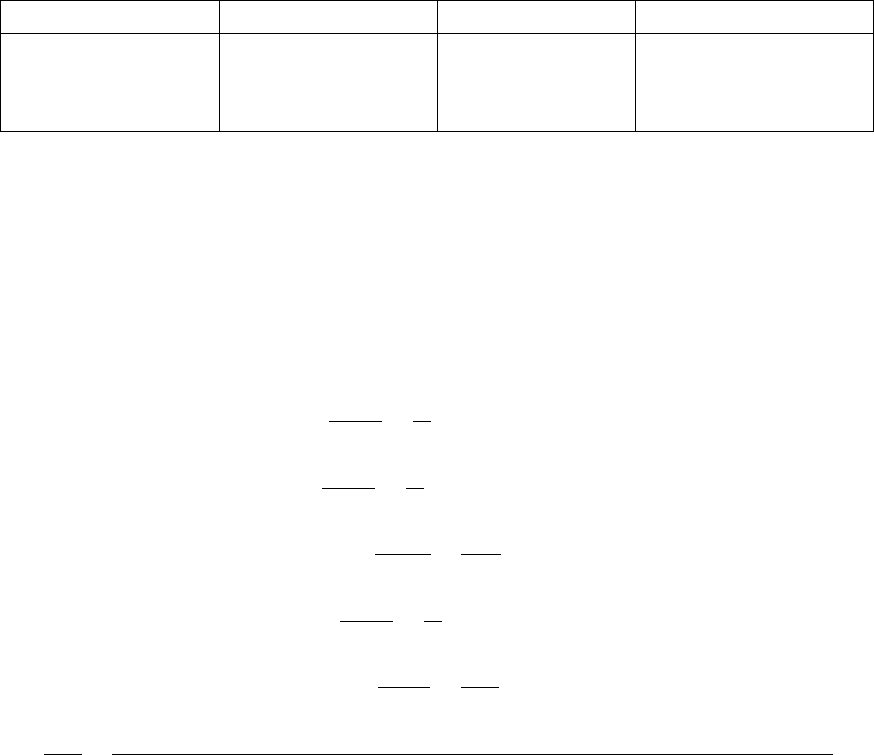
Зависимости концентраций
реагирующих веществ
от времени реакции
Зависимость температуры
реакционной смеси
от времени реакции
0 200 400
0
0.5
1
CA ( )
CB ( )
0 200 400
20
30
40
t ( )
Температура реакционной смеси в конце процесса:
t 1
38.3 C
Концентрация вещества B
в реакционной смеси в конце процесса:
CB 1
0.5
кмоль
м
3
В рассмотренном примере продемонстрирован метод решения
систем дифференциальных с использованием функции
Odesolve([Vf], x, Vb/b, [step]) ,
которая возвращает функцию (или вектор функций Vf) переменной х,
являющуюся(щийся) решением ОДУ (или системы ОДУ) при задан-
ных начальных условиях. Vf требуется лишь в том случае, когда ре-
шается система дифференциальных уравнений, для определения оче-
редности вывода искомых функций. Vb – это двухэлементный вектор-
столбец, который определяет начальную и конечную точку интервала
интегрирования; альтернативно b задает конечную точку интервала
интегрирования, подразумевая, что начальная точка – нулевая. step
(задается, если необходимо) – число шагов.
Указанная функция реализует метод Рунге-Кутта с фиксирован-
ным шагом, причем результатом решения сразу являются функции,
интерполирующие табличные значения.
Следует обратить внимание на то, что в приведенном примере вы-
ражение для
d
dt
записано в двух строках лишь потому, что в силу своей
громоздкости оно не вмещается на страницу целиком. Однако в Mathcad
его следует вводить целиком в одну строку без каких-либо пропусков.
53
3.1.2. Математическая модель проточного реактора полного
смешения
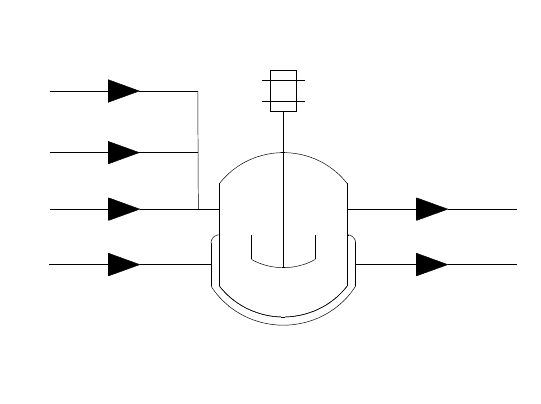
Проточный реактор полного смешения – это открытая система,
имеющая тепломассообмен с окружающей средой, в которой гидро-
динамический режим близок к модели идеального смешения. Матема-
тическая модель такого реактора основана на допущении о безгради-
ентности – отсутствии градиента параметров состояния и свойств ре-
акционного потока во
всем объеме реакционно-
го пространства в любой
момент времени. Приня-
тие такого допущения об
идеальной однородности
потока справедливо в ус-
ловиях высокой интен-
сивности перемешивания
реакционной среды в ем-
костных аппаратах с со-
отношением H/D 1
(рис. 10).
Для политропического реактора математическая модель пред-
ставляет собой следующую совокупность уравнений:
– уравнение общего материального баланса
p
k
kk
1
00
, (13)
где
k0
– объемный расход k-го входного потока, [объем/время];
k0
– плотность k-го входного потока, [масса/объем]; p – число вход-
ных потоков; – объемный расход выходного потока, [объем/время];
– плотность выходного потока, [масса/объем];
– уравнения покомпонентных материальных балансов
m
j
jjii
p
k
kik
rVCC
11
00
, (14)
где
ki
C
0
– концентрация i-го вещества в k-м входном потоке, [количе-
ство вещества/объем];
i
C – концентрация i-го вещества в реакторе и
на выходе из него, [количество вещества/объем]; при стехиометриче-
V, t, C
i
Gc, Cc, tcн Gc, Cc, tcк
,
t, C
i
01
,
t
01
, C
01i
02
,
t
02
, C
02 i
0k
,
t
0k
, C
0k i
Рис. 10. Проточный реактор полного смешения

54
ском коэффициенте знак «+» ставится, если i-е вещество расходуется
по j-й реакции, знак «–» – в противном случае;
– уравнение теплового баланса при использовании теплоносите-
ля, изменяющего агрегатное состояние
p
k
m
j
n
i
cMiijj
n
i
Mikikk
ttKFCCtrqVCCt
1 1 11
000
, (15)
где
k
t
0
– температура k-го входного потока, С; t – температура реак-
ционной смеси в реакторе и на выходе из него, С; при тепловом эф-
фекте реакции знак «+» ставится, если j-я реакция экзотермическая,
знак «–» – в противном случае;
– уравнение теплового баланса при использовании теплоносите-
ля, не изменяющего агрегатное состояние
p
k
m
j
n
i
сс
Miijj
n
i
Mikikk
tt
tKFCCtrqVCCt
1 1 1
к,н,
1
000
2
.(16)
В случае адиабатического реактора уравнение теплового балан-
са перепишется в виде
p
k
m
j
n
i
Miijj
n
i
Mikikk
CCtrqVCCt
1 1 11
000
. (17)
В случае, если исходные реагенты подаются при температуре
процесса, а тепловой эффект химических реакций полностью компен-
сируется теплообменом с теплоносителем (или окружающей средой),
либо реакции протекают в среде кипящего растворителя, для матема-
тического описания реактора достаточно составить систему уравне-
ний (13), (14).
Пример. Определить производительность реактора, описанного
в примере в подразделе 3.1.1, если он будет работать в непрерывном
режиме и в нем будет протекать та же система реакций. Смесь посту-
пает в реактор при температуре t
0
= 20С, время пребывания = 200 с.
Решение. Реактор работает в политропических условиях, при-
чем в него поступает лишь один входной поток. При допущении, что
плотность реакционной смеси не изменяется значительно в ходе про-
цесса, математическая модель реактора будет иметь вид

55
н,к,
к,н,
к,н,
0
120000
120
210
2
2
)(
ссcc
сс
сс
MDDMBBMAA
MDDMBBMAA
BB
AA
ttCG
tt
tKF
tt
tKFCCCCCCt
rrHVCCCCCCt
rrVCC
rrVCC
K F t
tcn tck
2
Gc Cc tck tcn( )
t CA CMA CB CMB CD0CMD( ) K F t
tcn tck
2
t0 CA0 CMA CB0CMB CD0 CMD( ) V H CA CB t( ) r2 CA CB t( ) r1 CA CB t( )( )
CB 0CA 0 CB0 CB( ) V r2 CA CB t( ) r1 CA CB t( )( )
CA CB 1 CA0 CA( ) V r1 CA CB t( ) r1 CA CB t( )( )
Given
- задаем начальные приближения
искомых переменных
tck 10t 20CB 0CA 1
Решение системы алгебраических уравнений
покомпонентных материальных и теплового балансов реактора:
- определяем объемный расход
реакционной смеси
м
3
c
4 10
3
V
c 200
При расчете будем использовать исходные данные
и вспомогательные функции, заданные в примере расчета
периодического реактора в подразделе 3.1.1.
Производительность
реактора по веществу B:
CA
CB
t
tck
MinErr CA CB t tck( )
CA
CB
t
tck
0.543
0.457
38.304
9.657
CB 10
3
1.826
моль
c

56
3.1.3. Математическая модель проточного реактора полного
вытеснения
Проточный реактор полного вытеснения – это открытая систе-
ма, имеющая тепломассообмен с окружающей средой, в которой гид-
родинамический режим близок к модели идеального вытеснения. Эта
модель основана на следующих допущениях:
1) реакционная смесь идеально перемешана в сечении, перпен-
дикулярном движению потока (т.е. состав и температура в сечении
одинаковы);
2) перемешивание в направлении движения потока (продольное
перемешивание) отсутствует.
Первое допущение справедливо в условиях высоких скоростей
потока (Re>10
4
); второе – выполняется при условии, что высота (дли-
на) реактора значительно больше его диаметра (H/D>20), либо в слу-
чае, когда поток движется через слой зернистого материала.
Принятым допущениям удовлетворяют такие промышленные
реакторы как пустотелый трубчатый (рис. 11, а), кожухотрубчатый со
стационарным слоем гетерогенного катализатора в трубах (рис. 11, б),
колонного типа со стационарным слоем гетерогенного катализатора
(рис. 11, в).
0
,
t
0
, C
0i
,
t, C
i
0
,
t
0
, C
0i
,
t, C
i
0
,
t
0
, C
0i
,
t, C
i
Gc, Cc, tcн
Gc, Cc, tcк
а) б) в)
Рис. 10. Типы проточных реакторов полного вытеснения
Поскольку значения параметров состояния и свойств изменяют-
ся по длине реактора, его математическое описание составляется для
57
элементарного объема реакционного пространства
Sdx
dV
, где S –
площадь поперечного сечения потока.
Рассмотрим проточный реактор полного вытеснения, в котором
протекают химические превращения в жидкой фазе. В этом случае
можно принять, что объемный расход реакционной массы не изменя-
ется по длине реактора ( const
0
), и система уравнений МТБ с
учетом химической кинетики будет иметь вид:
– уравнения покомпонентных материальных балансов
m
j
jji
i
r
dV
dC
1
1
, (18)
где при стехиометрическом коэффициенте знак «+» ставится, если i-е
вещество образуется по j-й реакции, знак «–» – в противном случае;
– уравнение теплового баланса для политропического реактора
при использовании теплоносителя, изменяющего агрегатное состоя-
ние (рис. 11, б: const
к,н,
cсс
ttt ), либо при существенных тепло-
потерях в окружающую среду (рис. 11, а, в:
c
t – температура окру-
жающей среды)
n
i
Mii
c
n
i
Mii
m
j
jj
CCd
ttK
CC
rq
dV
dt
1
вн
1
1
4
, (19)
где d
вн
– внутренний диаметр реактора (труб реактора), м; при тепло-
вом эффекте реакции знак «+» ставится, если j-я реакция экзотермиче-
ская, знак «–» – в противном случае;
– уравнение теплового баланса для политропического реактора
при использовании теплоносителя, не изменяющего агрегатное со-
стояние (рис. 11, б), должно быть дополнено уравнением, описываю-
щим изменение температуры теплоносителя
cc
cc
CGd
ttK
dV
dt
вн
4
. (20)
– уравнение теплового баланса для адиабатического реактора
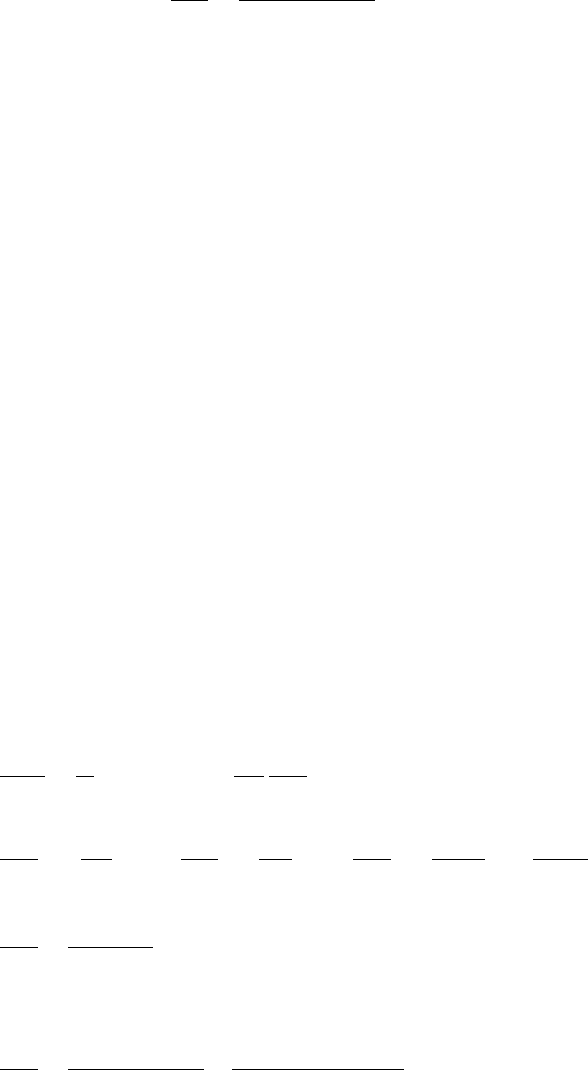
58
n
i
Mii
m
j
jj
CC
rq
dV
dt
1
1
. (21)
В случае, если в реакторе соблюдается изотермический тепло-
вой режим, математическое описание ограничивается уравнениями
материального баланса (18).
Представленная математическая модель может быть использо-
вана и для описания газофазного процесса, если он протекает в изо-
термическом режиме, без изменения общего числа молей компонен-
тов реакционной смеси, а потеря давления на преодоление гидравли-
ческих сопротивлений при прохождении смеси через реактор пренеб-
режительно мала по сравнению с общим давлением в системе.
Однако для большинства газофазных процессов, протекающих в
проточном реакторе полного вытеснения, приходится учитывать из-
менение объемного расхода потока по длине аппарата, обусловленное
изменением температуры, давления и (или) числа газовых молей ре-
акционной смеси при движении через аппарат. Взаимосвязь между
указанными параметрами состояния газового потока при относитель-
но невысоких давлениях (до 1 МПа) с удовлетворительной точностью
описывается уравнением Менделеева–Клапейрона.
С учетом вышесказанного, математическую модель реактора
вытеснения для газофазных процессов в общем виде можно предста-
вить следующим образом:
;
4
,
2
,
,
1
11
1
1
3
2
,
,,
1
n
i
Miiвн
c
n
i
Mii
m
j
jj
n
i
ii
вн
Pt
tCPC
i
m
j
jji
i
CCd
ttK
CC
rq
dV
dt
MC
Sd
dV
dP
dV
dC
CdV
dP
PdV
dt
tdV
d
dV
d
C
r
dV
dC
(22)

59
где
P
RC
t
PC
,
; (23)
2
,
273
P
tRC
P
tC
; (24)
P
tR
C
Pt
273
,
; (25)
P – общее давление, Па;
n
i
i
CC
1
, моль/м
3
; – коэффициент трения;
M
i
– молярная масса i-го компонента реакционной смеси, кг/моль;
R=8.31 Дж/(моль·К) – универсальная газовая постоянная.
В справочной литературе скорости газофазных химических ре-
акций часто выражены через парциальные давления реагирующих
веществ, однако кинетические уравнения в такой форме не всегда
пригодны для составления математических моделей реакторов. По-
этому целесообразно осуществлять переход от парциальных давлений
(p
i
) реагирующих веществ к их концентрациям (C
i
) по формуле
273
tRCp
ii
. (26)
Расчет реакторов полного вытеснения поясним на следующих
примерах.
Пример А. В проточном реакторе полного вытеснения адиаба-
тического типа протекает система жидкофазных реакций
A
+ B
r
1
R
2S
+ 2B
r
3
2U
r
2
скорости которых описываются формальной кинетикой. Кинетиче-
ские и термодинамические параметры реакций представлены в
табл. 1.
Начальные концентрации веществ: С
0А
= 1 кмоль/м
3
, С
0В
=
0.5 кмоль/м
3
, С
0U
= С
0R
= С
0S
= 0, концентрация инертного вещества
(растворителя) С
0D
= 15 кмоль/м
3
; теплоемкости веществ
[кДж/(кмоль·К)]: С
МА
= 74, С
МВ
= 68, С
МU
= 70, С
МR
= 78, С
МS
= 85,
60
Таблица 1
Кинетические и термодинамические параметры реакций
Номер реакции k
0
, кмоль
(1–n)
·c
–1
E, кДж/кмоль ΔH
293
, кДж/кмоль
1 10
8
49860 – 45000
2 10
7
53240 52500
3 10
9
64790 – 64000
С
МD
= 61 (не являются функцией температуры). Начальная температу-
ра реакционной смеси t
0
= 40С. Объемный расход реакционной смеси
υ = 0.5 м
3
/с.
Определить объем реактора, при котором выход вещества R
наибольший.
Решение. С соответствии с уравнениями (18) и (21) математи-
ческая модель реактора будет иметь вид
,
,
2
,
1
,
2
,2
1
,
1
0
332211
3
31
2
31
21
MDDMSSMRRMUUMBBMAA
S
R
U
B
A
CCCCCCCCCCCC
rHrHrH
dV
dt
r
dV
dC
rr
dV
dC
r
dV
dC
rr
dV
dC
rr
dV
dC
при следующих начальных условиях:
.0
,0
,0
,0
,0
,0
0
0
0
0
0
0
tt
CC
CC
CC
CC
CC
SS
RR
UU
BB
AA
