Яревский Е.А. Численные методы для дифференциальных уравнений в частных производных
Подождите немного. Документ загружается.


values at two corresponding vertexes only. Therefore, the basis function are
continuous.
The biquadratic Lagrange elemental functions Any function U(ξ, η)
on the rectangle is approximated with the biquadratic basis as
U(ξ, η) =
3
X
i=1
3
X
j=1
c
i,j
N
i,j
(ξ, η),
where
N
i,j
(ξ, η) = N
2
i
(ξ)N
2
j
(η), i, j = 1, 2, 3.
Figure 18: The biquadratic elemental functions for the vertex, edge and
surface.
The one-dimensional elemental functions are given by
N
2
1
(ξ) = −ξ(1 − ξ)/2, N
2
2
(ξ) = ξ(1 + ξ)/2,
59
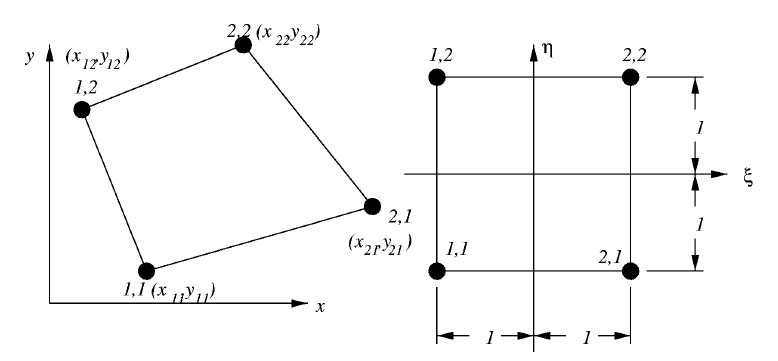
N
2
3
(ξ) = (1 − ξ
2
), −1 ≤ ξ ≤ 1.
So we can see that the biquadratic function N
i,j
(ξ, η) is generally written as
N
i,j
(ξ, η) = a
1
+ a
2
ξ + a
3
η + a
4
ξ
2
+ a
5
ξη + a
6
η
2
+
+a
7
ξ
2
η + a
8
ξη
2
+ a
9
ξ
2
η
2
.
It contains s ome terms of the order higher than two, they ale collected in the
second line. However, an arbitrary polynomial of the second degree only can
be represented by N
i,j
(ξ, η). According to Theorem 4-2, we have here the
approximation of the second order. The higher degree terms do not improve
the approximation. In fact, they are redundant, and might even result in the
degradation of the numerical accuracy and stability.
We have constructed the basis function on the computational plane, and
need to transform them into the physical plane. The mapping of the canonical
square onto the physical rectangle (x
ij
, y
ij
) is given with the functions N
1
i
x
y
=
2
X
i=1
2
X
j=1
x
ij
y
ij
N
1
i
(ξ)N
1
j
(η).
Figure 19: The mapping of the canonical square onto the physical rectangle.
60

For example, the edge η = −1 maps onto the edge (x
11
, y
11
) − (x
21
, y
21
):
x
y
=
x
11
y
11
1 − ξ
2
+
x
21
y
21
1 + ξ
2
. (54)
It is important that the vertexes (x
12
, y
12
) and (x
22
, y
22
) do not enter Eq.(54)
and do not affect this transformation. Therefore, the continuity of the basis
functions is preserved with this mapping.
61

Lecture 6
Multidimensional FEM. The hierarchical finite elements. Three-dimensional
elements. The interpolation errors.
16 The hierarchical elements
In order to study the methods for the construction of the multidimensional
hierarchical finite elements, we restrict ourselves to the simpler case of the
rectangles. We describe the hierarchical basis for the square. These functions
can be then recalculated for an arbitrary rectangle with the transformation
described in the previous lecture.
The order p basis consists of the different types of functions. Those
functions are linked with the vertices, edges and the center of the square.
Let us describe them.
Elemental functions for the vertices (4 bilinear functions):
N
1
ij
(ξ, η) = N
1
i
(ξ)N
1
j
(η), i, j = 1, 2.
Elemental functions for the edges (linked with the center of edges, 4(p − 1)
functions existing for p ≥ 2):
N
k
31
(ξ, η) = N
1
1
(η)N
k
(ξ), N
k
13
(ξ, η) = N
1
1
(ξ)N
k
(η),
N
k
32
(ξ, η) = N
1
2
(η)N
k
(ξ), N
k
23
(ξ, η) = N
1
2
(ξ)N
k
(η).
In the last equations the index k spans the values k = 2, 3...p. The function
N
k
(y) are defined as
N
k
(y) =
r
2k − 1
2
Z
y
−1
P
k−1
(t) dt.
Here P
k−1
(t) is the Legendre polynomial of the de gree k − 1. It is easy to
check that N
k
(−1) = N
k
(1) = 0, so each elemental function for the edges is
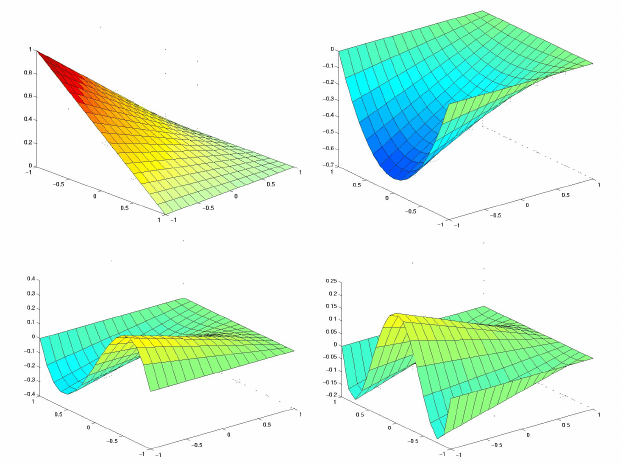
identically zero on three edges out of four. Few of these functions are plotted
in Fig. 20.
62
Elemental functions linked with the center of the square (3,3). These (p −
2)(p − 3)/2 functions existing for p ≥ 4) can be described in terms of the
function N
400
33
:
N
400
33
= (1 − ξ
2
)(1 − η
2
).
For p = 4, only this f unction enters the expansion. For the polynomial
degrees p = 5, 6, the hierarchical functions are defined as
N
510
33
= N
400
33
P
1
(ξ), N
501
33
= N
400
33
P
1
(η),
N
620
33
= N
400
33
P
2
(ξ), N
611
33
= N
400
33
P
1
(ξ)P
1
(η), N
602
33
= N
400
33
P
2
(η).
The upper index kλµ of the function consists of the total polynomial degree
and the degrees of the additional polynomials in ξ and η coordinates so that
k = λ + µ + 4. Few of these functions are plotted in Fig. 21. For the higher
polynomial degrees p > 6, the functions are introduced in the similar way.
Figure 20: The hierarchical functions for the vertex and for the edges (k =
1, 2, 3, 4).
63

The solution in terms of the hierarchical basis is expanded as follows:
U(ξ, η) =
2
X
i=1
2
X
j=1
c
1
ij
N
1
ij
+
p
X
k=2
"
2
X
j=1
c
k
3j
N
k
3j
+
2
X
i=1
c
k
i3
N
k
i3
#
+
p
X
k=4
X
λ+µ=k−4
c
kλµ
33
N
kλµ
33
.
The total number of the functions in this representation can be calculated as
4 + 4(p − 1)
+
+
(p − 2)
+
(p − 3)
+
2
, where q
+
= max(q, 0).
It is interesting to compare the total number of the function for three
basises of the order p: the direct product basis and the hierarchical basis in
the canonical square, and the minimally admissible set which coincides with
the basis in the canonical triangle. These number are presented in the table:
degree p 1 2 3 4
the triangle basis 3 6 10 15
the direct product basis 4 9 16 25
the hierarchical basis 4 8 12 17
One can see that both basises for the square are not optimal with respect to
the number of functions. For the low polynomial degrees p = 1, 2, they are
very similar, and the number of the functions essentially exceeds that for the
triangle. For higher p, however, quality of the hierarchical basis improves
and the number of the functions asymptotically converges to the optimal
value. Quality of the direct product basis stays the same, the number of the
functions essentially exceeds the optimal value.
17 The three-dimensional elements
17.1 The tetrahedron
For the three-dimensional case, the number of polynomials of the degree p is
equal to
n
p
=
(p + 1)(p + 2)(p + 3)
6
.
64
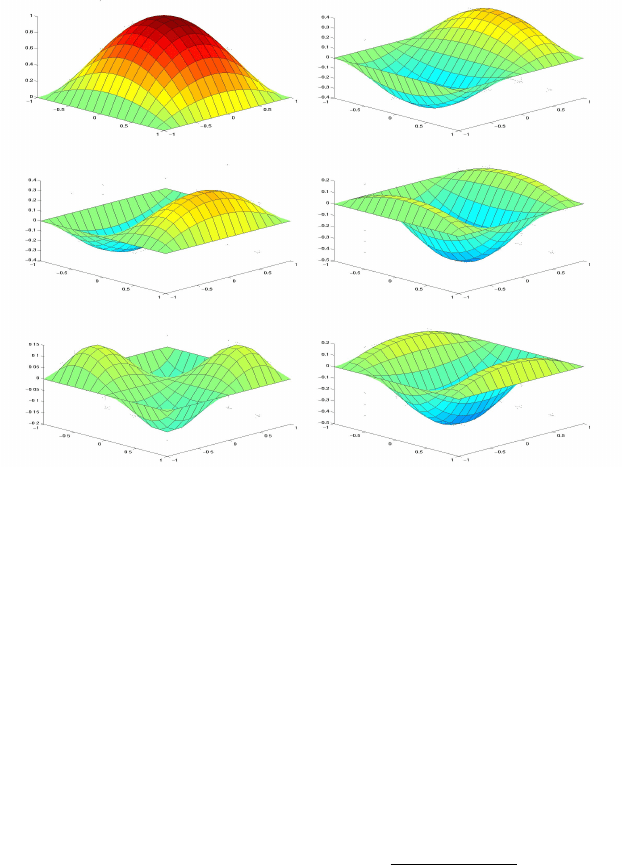
Figure 21: The hierarchical elemental functions linked with the center of the
square N
kλµ
33
, λ + µ = k − 4 (k = 4, 5, 6).
The construction of the elemental functions is done in the same way as for
the two-dimensional case s o we give here the formulas for the linear Lagrange
elements only.
For the tetrahedron, the Lagrange conditions
N
j
(x
k
, y
k
, z
k
) = δ
jk
, j, k = 1, 2, 3, 4,
lead to the following representation for the linear functions:
N
j
(x, y, z) =
D
klm
(x, y, z)
C
jklm
.
Here (jklm) is a permutation of (1,2,3,4) numbers, and the determinants
D
klm
and C
jklm
are written as
D
klm
= det
1 x y z
1 x
k
y
k
z
k
1 x
l
y
l
z
l
1 x
m
y
m
z
m
, C
jklm
= det
1 x
j
y
j
z
j
1 x
k
y
k
z
k
1 x
l
y
l
z
l
1 x
m
y
m
z
m
.
65
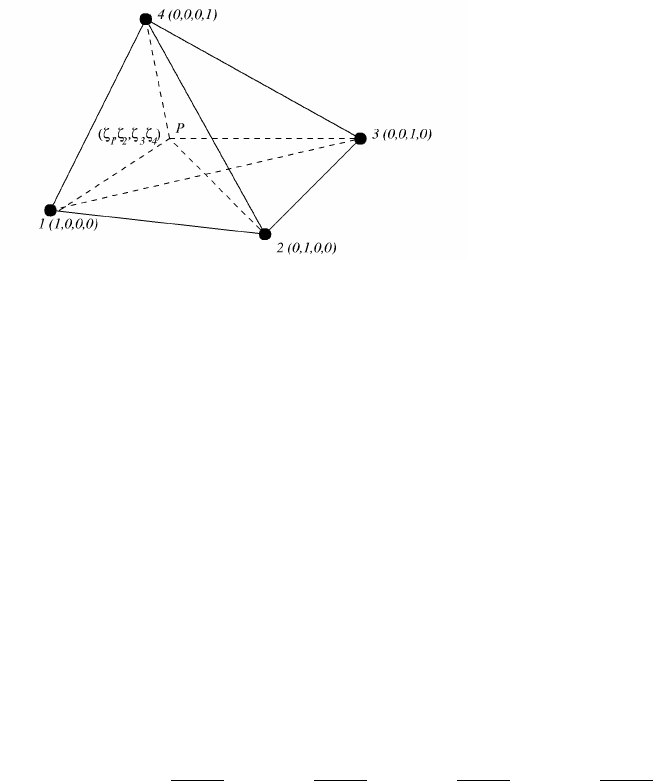
Figure 22: The nodes for the linear elemental function on the tetrahedron
and barycentric coordinates.
The projection of the solution U on the element can be expanded in terms
of these functions as
U(x, y, z) =
4
X
j=1
c
j
N
j
(x, y, z).
The barycentric coordinates (also known as the volume coordinates) are
defined as
ζ
j
= N
j
(x, y, z), j = 1, 2, 3, 4.
These coordinates also give the volumes of the corresponding tetrahedrons
with the vertex at the point P :
ζ
1
=
V
P 234
V
1234
, ζ
2
=
V
P 134
V
1234
, ζ
3
=
V
P 124
V
1234
, ζ
4
=
V
P 123
V
1234
.
As in the two-dimensional case, the barycentric coordinates are redundant.
The inverse coordinate transformation can be defined with the formula
x
y
z
1
=
x
1
x
2
x
3
x
4
y
1
y
2
y
3
y
4
z
1
z
2
z
3
z
4
1 1 1 1
ζ
1
ζ
2
ζ
3
ζ
4
.
The last line in this equation shows us the redundancy of the barycentric
coordinates.
66
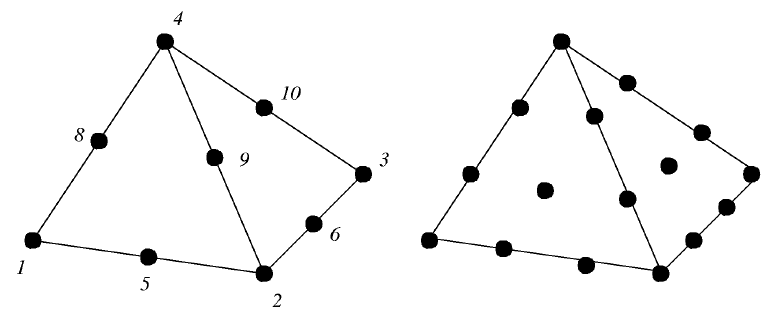
Figure 23: The nodes for the quadratic and cubic elemental functions on the
tetrahedron.
17.2 The cube
The canonical cube is defined as
{(ξ, η, ζ) : −1 ≤ ξ, η, ζ ≤ 1}.
The elemental function for the node (ijk) is written as the direct product of
the one-dimensional linear functions:
N
ijk
= N
i
(ξ)N
j
(η)N
k
(ζ).
18 The interpolation error
The estimation of the interpolation errors will b e done in two steps:
• the interpolation error estimation with polynomials on the canonical
element
• the recalculation of the interpolation errors from the canonical to the
physical element.
67

Figure 24: The nodes for the tri-linear tri-quadratic elemental functions on
the cube.
For the sake of simplicity, let us consider the two-dimensional case. We
expand a function on the canonical element in terms of the elemental func-
tions
U(ξ, η) =
n
X
j=1
c
j
N
j
(ξ, η). (55)
Then the interpolation error on the canonical element is estimated with the
following
Theorem 1: Let p be the maximal integer number, such that Eq.(55) is exact
for any polynimial of the degree p. Then for the canonical element Ω
0
there
exists C > 0 such that
|u − U|
s,Ω
0
≤ C|u|
p+1,Ω
0
,
∀u ∈ H
p+1
(Ω
0
), s = 0, 1...p + 1.
where |u|
s,Ω
0
stands for the Sobolev quasinorm.
68
