Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.

5.3 Fanno and Rayleigh Lines
0
1
2
11
0
°
¿
°
¾
½
°
¯
°
®
¸
¸
¹
·
¨
¨
©
§
hh
k
h
c
dh
ds
v
(5.3.8)
This gives the entropy
s
maximum for
12
0
khh . Furthermore, this
12
0
khh is substituted into Eq. (5.3.2) to give
kRT
kTc
khu
p
1
1
2
(
5.3.9)
Equation (5.3.9) shows that at the maximum entropy, the flow is at the
sonic, i.e.
1
2222
aukRTuM . Similarly, we can write the gradient
of the
line from Eq. (5.3.8) in terms of the Mach number
»
¼
º
«
¬
ª
2
2
2
11
M
M
a
k
dh
ds
(5.3.10)
and as a result Eq. (5.3.10) yields the following relations for 1!k
0!
dh
ds
, 1!
M
(supersonic)
0
dh
ds
, 1
M
(sonic)
0
dh
ds
, 1
M
(subsonic)
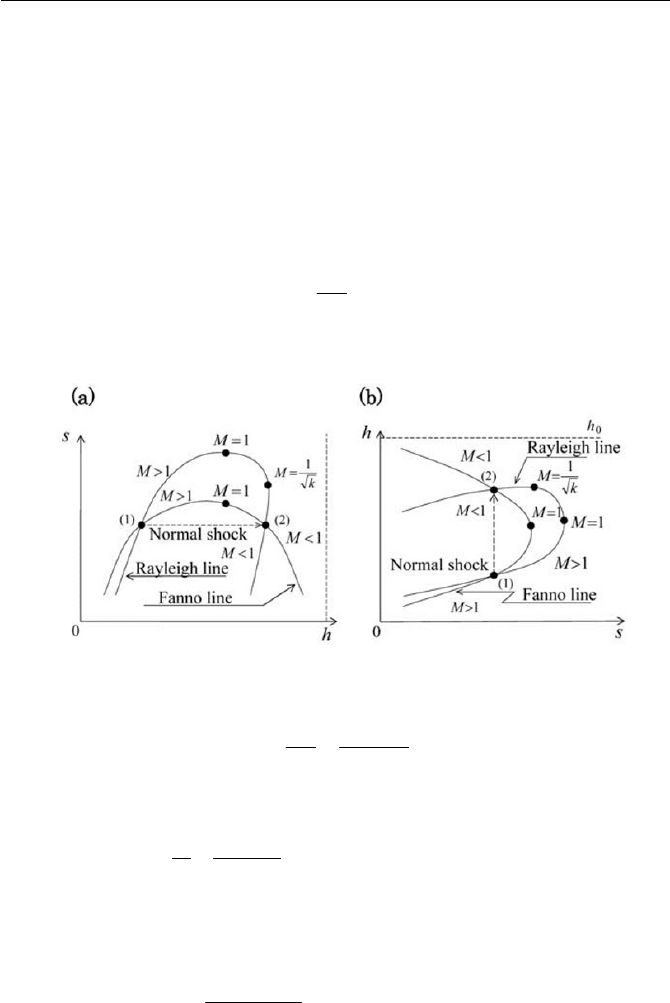
as indicated in Fig. 5.8(a) and (b). The relations characterize the Fanno line.
The equations of the Rayleigh line are also derived, on the other hand,
from the mass continuity and the momentum equation for frictionless flow,
lifting the adiabatic condition. The flow under consideration is similarly
one dimensional with steady internal flow. Instead of the energy equation,
we use the momentum equation per unit area (the momentum flux) from
Eq. (4.1.47), i.e.
Appuum
2112
2112
ppuuu
U
243
5 Compressible Flow
and by the mass continuity of Eq. (5.3.1);
12
uu
U
U
, we have the expres-
sion
.const fpuu
U
(5.3.11)
where f is called the impulse or thrust function as it is kept constant for
frictionless flow through the channel. Using the continuity of Eq. (5.3.1)
again, we may be able to modify Eq. (5.3.11) to write
p
explicitly with
the formula that follows
U
2
G
fp
(5.3.12)
For an ideal gas, the enthalpy is written by the following formula
Fig. 5.8 Fanno and Rayleigh lines
1
k
kp
R
p
cTch
pp
UU
(5.3.13)
so that
k
hk
p
1
U
(5.3.14)
Combining Eq. (5.3.12) with Eq. (5.3.14) and eliminating
U
, we can ob-
tain an expression for enthalpy as
2
2
1 Gk
pfpk
h
(5.3.15)
Nevertheless to convey the essence of the subject, it is required to write
p
in Eq. (5.3.15) in terms of the entropy in a thermodynamic system. For
244
5.3 Fanno and Rayleigh Lines
an ideal gas, the pressure
p
is a function of any two thermodynamics pa-
rameters, i.e.
shpp , . Considering Eqs. (2.5.6) with (2.5.17) by inte-
grating between the state points, we have
°
¿
°
¾
½
°
¯
°
®
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
k
v
p
p
css
U
U
2
2
2
ln
(5.3.16)
and it follows that
¸
¸
¹
·
¨
¨
©
§
¸
¹
·
¨
©
§
¸
¸
¹
·
¨
¨
©
§
p
c
ss
k
k
e
p
p
h
h
2
1
22
(5.3.17)
where we have used,
22
TThh . Equation (5.3.17) can be further sim-
plified into
1
2
¸
¸
¹
·
¨
¨
©
§
°
¿
°
¾
½
°
¯
°
®
k
k
c
s
p
ehCp
(5.3.18)
where
2C is a constant defined at one state point. The equation of the
Rayleigh line is now to be derived by substituting Eq. (5.3.18) into Eq.
(5.3.15) to give
0
1
2
2
2
1
2
1
2
¸
¹
·
¨
©
§
°
¿
°
¾
½
°
¯
°
®
°
¿
°
¾
½
°
¯
°
®
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
h
k
k
C
a
eh
C
f
eh
k
k
c
s
k
k
c
s
pp
(5.3.19)
In Fig. 5.8(a) and (b), Rayleigh lines are displayed, having common states
with the Fanno lines. As in the case of Fanno lines, we are similarly able to
obtain the condition at
s
to be a maximum by differentiating
s
in Eq.
(5.3.19) with respect to h as
¸
¹
·
¨
©
§
TkM
M
dh
ds 11
2
2
(5.3.20)
where we used the relation in Eq. (5.3.9) similar to the case of the Fanno
line. It is denoted that Eq. (5.3.20) is readily obtained by Eqs. (5.3.14)
and (10) in Exercises 5.3 together with the thermodynamics relation
245
5 Compressible Flow
Tdsdhdp
U
derived from Eq. (2.5.15). As shown in Fig. 5.8(a) and (b),
at 1
M
the entropy
s
reaches the maximum, yielding the flow character-
istics for
1
2
!kM as follows
0!
dh
ds
, 1!
M
(supersonic)
0
dh
ds
, 1
M
(sonic)
0
dh
ds
, 11 Mk (subsonic)
It is readily confirmed that at
kM 1
, the enthalpy becomes maximum
and for
11 Mk ,
dsdh
is negative, while everything other than this
region
dsdh
is positive. In Rayleigh flows, as indicated by the Rayleigh
line, the increase of entropy is due to heat given from outside the system,
since no friction is assumed. Therefore, in comparison with the Fanno flow,
which is represented by the Fanno line, self-heating of a compressible flow
has an effect to encourage the flow to reach 1
M
, and this implicitly
suggests the friction effect of the Fanno flow.
As we will see later in this chapter, a normal shock is characterized
with the mass continuity equation, the momentum equation and the energy
equation. Thus, the thermodynamic states represented at points (1) and (2)
in Fig. 5.8(a) and (b), where the Fanno and Rayleigh lines across for a
given mass flux
G
, satisfy the three equations for a normal shock. This
fact represents that through the occurrence of the normal shock the entropy
increases from points (1) to (2) of the thermodynamic states behind and
ahead of the normal shock respectively.
5.4 Normal Shock Waves
In a Laval tube, as studied in the previous section, when the exit pressure
is well below the reservoir pressure, there is a discontinuity in pressure as
observed in Fig. 5.5(a) and (b). The discontinuity of pressure, density and
temperature that occurs in the direction of compressible flow is a promi-
nent feature of normal shock. Also for the points where Fanno and
Rayleigh lines cross, there is an entropy increase as verified in Fig. 5.8(a)
and (b). The points (1) and (2) in Fig. 5.8(a) and (b) meet the following
conditions
246
5.4 Normal Shock Waves
(2) constant cross sectional area through the shock
(3) ideal gas
(4) steady state flow
(5) adiabatic and frictionless
It may be further stated that for the points of cross-lines, the mass con-
tinuity, the momentum and the energy equations are simultaneously satis-
fied. The normal shock, the simplest case of a shock wave, is regarded and
is observed in experiments as a surface perpendicular to the direction of
flow. Through the shock there is sudden occurrence of discontinuous
change of flow properties and the flow is irreversible, so that, although the
adiabatic condition is held, the isentropic equations cannot be used. A state
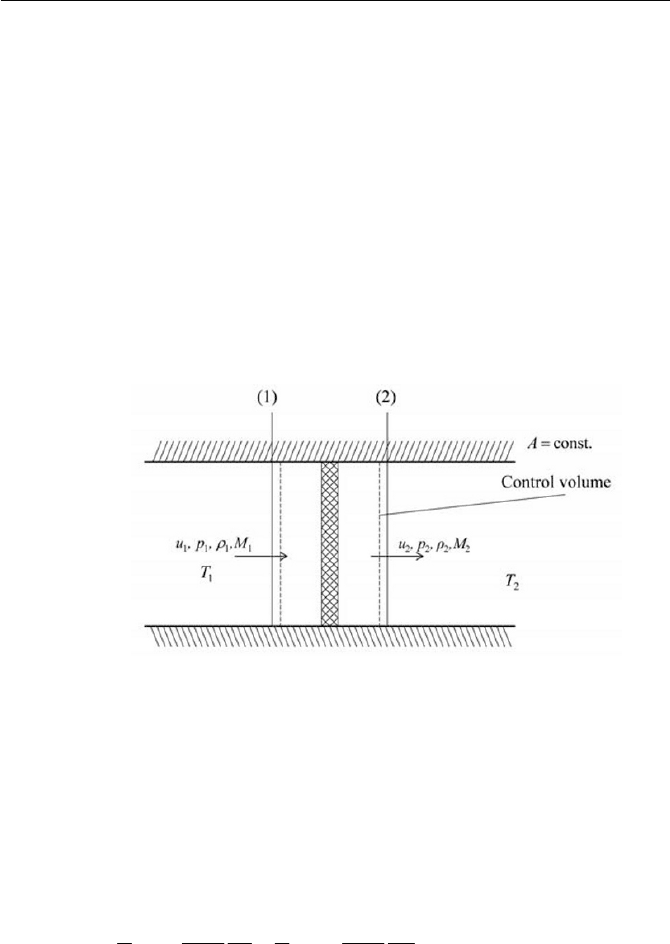
of flow for a normal shock is depicted in Fig. 5.9.
Fig. 5.9 Normal shock
The equations of mass continuity, momentum and energy are repeat-
edly written for a normal shock as
2211
uu
U
U
(5.4.1)
2
2
221
2
11
pupu
UU
(5.4.2)
2
2
2
2
1
1
2
1
12
1
12
1
UU
p
k
k
u
p
k
k
u
(5.4.3)
From Eqs. (5.4.1–5.4.3), we have a relationship among the flow properties
between states (1) and (2), respectively in front of and behind the normal
shock as follows
(1) one dimensional
247
5 Compressible Flow
1
2
1
2
2
1
1
2
11
11
ppkk
ppkk
u
u
U
U
(5.4.4)
With a definition of the speed of sound as Eq. (5.1.25), we can write Eq.
(5.4.4) in terms of a Mach number and its relevant forms such that
2
1
2
1
2
1
1
2
1
12
Mk
Mk
u
u
U
U
(5.4.5)
1
12
1
1
2
1
2
2
2
1
1
2
k
kkM
kM
kM
p
p
(5.4.6)
2
1
2
2
1
2
1
2
2
2
1
1
2
1
1212
1
2
1
1
1
2
1
1
Mk
MkkkM
Mk
Mk
T
T
(5.4.7)
The formula of Eq. (5.4.4) that relates to pressure and density across a
normal shock is known as the Rankine-Hugoniot relationship. This rela-
tionship stands for a normal shock wave of any strength without taking in
account of any internal structure of the wave.
The equation of a state combined with the thermodynamic expression
for entropy change is given as Eq. (5.3.16) and causes the entropy increase
as
»
¼
º
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
1
2
1
2
12
lnln
U
U
k
p
p
css
v
(5.4.8)
Substituting Eq. (5.4.4) into Eq. (5.4.8), and denoting
1
2
ppp
G
and
12
sss
G
, we can expand Eq. (5.4.8) to give
4
3
1
2
2
0
12
1
p
p
p
k
k
cs
v
G
G
G
¸
¸
¹
·
¨
¨
©
§
(5.4.9)
Since in the normal shock wave, the entropy increases 0!s
G
, it gives a
condition that from Eq. (5.4.9), 0!p
G
. This for 0!p
G
implies that, from
Eqs. (5.4.4) to (5.4.7), the following relations must be met
248
5.4 Normal Shock Waves
2
1
u
u
,
1
2
p
p
,
1
2
T
T
,
1
2
U
U
1!
(5.4.10)
It is noted that
1
pp
G
in Eq. (5.4.9) is sometimes called the shock
strength and for 0!p
G
, the thermodynamic process is called the compres-
sion. That is to say, the normal shock wave is the compression wave and
the following conditions are to be thought:
(i) If the shock strength is small, i.e.
1
1
pp
G
, from Eq. (5.4.8) the flow
through the shock is isentropic, i.e. 0|s
G
.
(ii) Equation (5.4.4) may be written in the following form, by setting
1
2
ppp
G
and
1
2
U
U
G
U
2
1
21
UUGU
G
ppkp
(5.4.11)
and from the momentum equation of Eq. (5.4.2), we have
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
1
1
2
1
1
2
1
2
21
21
1
1
1
U
U
U
U
U
UU
p
k
p
p
ppk
u
(5.4.12)
Consequently according to Eq. (5.4.11), we can identify two conditions
for a normal shock wave: for a weak shock, i.e.
21
U
U
| and
21
pp | , Eq.
(5.4.12), which becomes
const.
2
2
1
1
1
|
UU
kpkp
u
(5.4.13)
which is the speed of sound, meaning that the shock propagates with the
speed of sound; for a very strong shock, i.e.
21
pp
and
21
U
U
, Eq.
(5.4.12) is certainly greater than the speed of sound, indicating that a very
strong shock may propagate faster than a weak shock.
When we consider the critical velocity
*
u , i.e. the velocity for the flow
reaching the speed of sound a , it will prove useful to write the energy
equation Eq. (5.4.3) as
2
2
2
2
2
1
1
2
1
12
1
12
1
12
1
*
a
k
k
p
k
k
u
p
k
k
u
UU
(5.4.14)
249
5 Compressible Flow
where
*
a is invariant between behind and ahead of a normal shock. It is
now desired to derive a useful expression for a normal shock. Eliminating
p
and
U
from Eqs. (5.4.1), (5.4.2) and (5.4.14), we can obtain a simple
expression as
2
21
*
auu
(5.4.15)
This is called as Prandtl relation. As an alternative, Eq. (5.4.15) can also be
written by
1
21
**
MM
(5.4.16)
Thus, from relationships in Eqs. (5.4.10) and (5.4.16), we have
1
1
!M
and
2
M , since
1
!
M
and
1
!
*
M
is respectively true. This indicates that a
normal wave can occur only if the upstream flow is supersonic.
It also appears, according to Eq. (5.4.16), that fo
1
M leads to
2112
uu
U
U
to reach an asymptote of
11 kk . If the value of
4.1 k
represents air, the maximum (the asymptote) is 6, meaning that air
cannot be compressed more than 6 times its original density by normal
shock, while
12
pp and
12
TT increase infinitely.
Mach number relations across a normal shock wave may be found in
the following relation
2
1
2
1
2
2
1
2
2
T
T
u
u
M
M
¸
¸
¹
·
¨
¨
©
§
(5.4.17)
so that with the aid of Eqs. (5.4.5) and (5.4.7) we have
12
21
2
1
2
1
2
2
kkM
Mk
M
(5.4.18)
Equation (5.4.18) also indicates that for 1
1
!M and
1!k
the flow is sub-
sonic behind a normal shock wave. As for air, for example, with 4.1
k ,
Eq. (5.4.18) can be reduced to
17
5
2
1
2
1
2
2
M
M
M
(5.4.19)
1
250
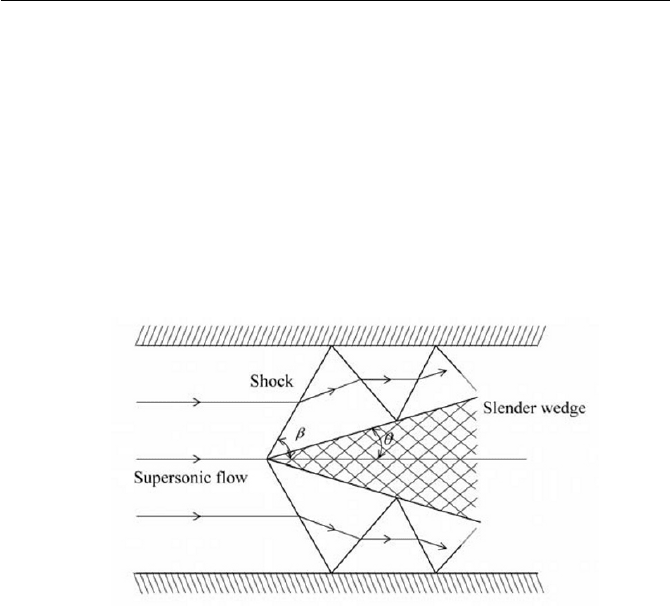
5.5 Oblique Shock Wave
5.5 Oblique Shock Wave
plane of the shock wave is inclined by an angle of
E
with respect to the
incoming flow direction. This plane shock wave, termed an oblique shock
wave, is attached to the nose of the wedge, and acts to turn the flow
through a semi-vertex angle (wedge angle) of
T
so that the flow becomes
parallel to the wedge downstream from the shock. An oblique shock wave
is often observed at the nose of a supersonic aircraft.
Fig. 5.10 Supersonic flow past a wedge
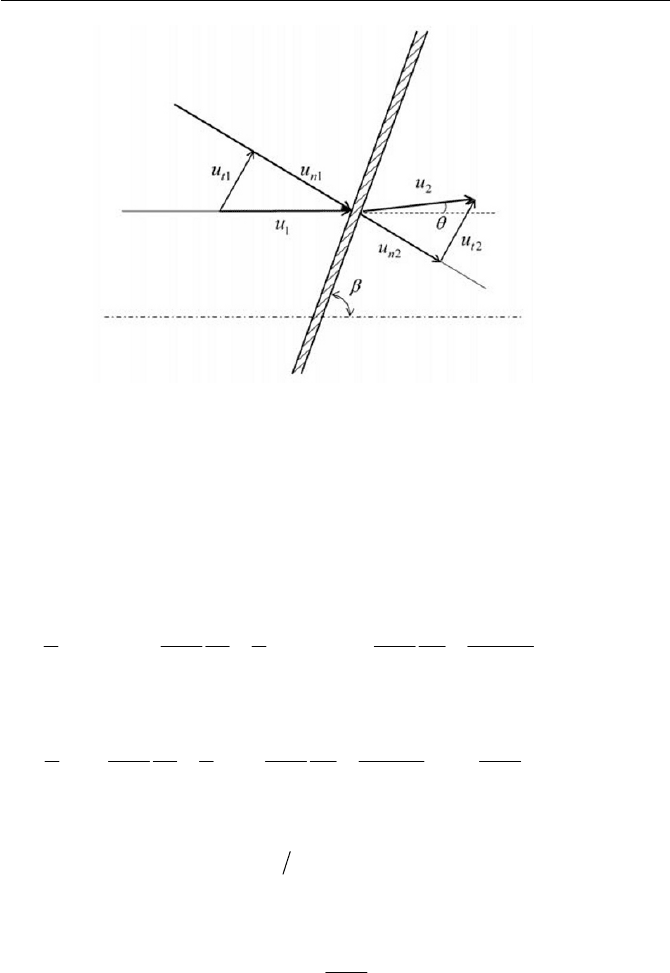
Figure 5.11 shows a schematic diagram of an oblique shock wave that
has been assigned kinematic properties. In dealing with an oblique shock
wave, mass continuity, momentum, and energy equations are to be solved
in the same manner as a normal shock wave. However, it should be kept in
mind that by conservation of momentum, since there is no pressure change
along the shock wave and there is no force acting on the fluid along the
shock wave plane, the tangential component of velocity
t
u is continuous
across the shock wave
222111 tntn
uuuu
U
U
(5.5.1)
Thus, with the aid of the relation
2211 nn
uu
U
U
(Eq. 5.4.1), we have
ttt
uuu
21
(5.5.2)
When a supersonic incompressible flow passes over a slender wedge, as
shown in Fig. 5.10, for example a plane shock wave is formed, when the
251
5 Compressible Flow
Fig. 5.11 The oblique shock
The normal components of velocity
1n
u and
2n
u are related to the normal
shock relations of the previous section. Therefore, the mass continuity,
momentum and energy equations in the normal direction to the shock are
written identically for an oblique shock when the flow properties, such as
pressure, density, temperature and etc, are related in the same way as with
the normal shock. Thus, it would be useful to write the energy equation as
2
2
2
2
2
2
2
1
1
2
1
2
1
1
1
12
1
12
1
*
a
kk
kp
k
k
uu
p
k
k
uu
tntn
UU
(5.5.3)
Furthermore, with the condition of Eq. (5.5.2) we have
¸
¹
·
¨
©
§
22
2
2
2
2
1
1
2
1
1
1
12
1
12
1
12
1
tnn
u
k
k
a
k
kp
k
k
u
p
k
k
u
*
UU
(5.5.4)
Equation (5.5.4) is exactly the same as Eq. (5.4.14) by replacing
2
*
a from
Eq. (5.4.14) with
11
22
kuka
t
*
, so that the Rankine-Hugoniot rela-
tionship of a normal shock wave can still be valid for the oblique shock.
The Prandtl relation for the oblique shock is also written as follows
22
21
1
1
tnn
u
k
k
auu
*
(5.5.5)
With the aid of the velocity diagram in Fig. 5.11, the velocity ratios for
n
u and
t
u are expressed in terms of the shock inclination angle
E
and the
velocity deflection angle
T
as
252
