Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.

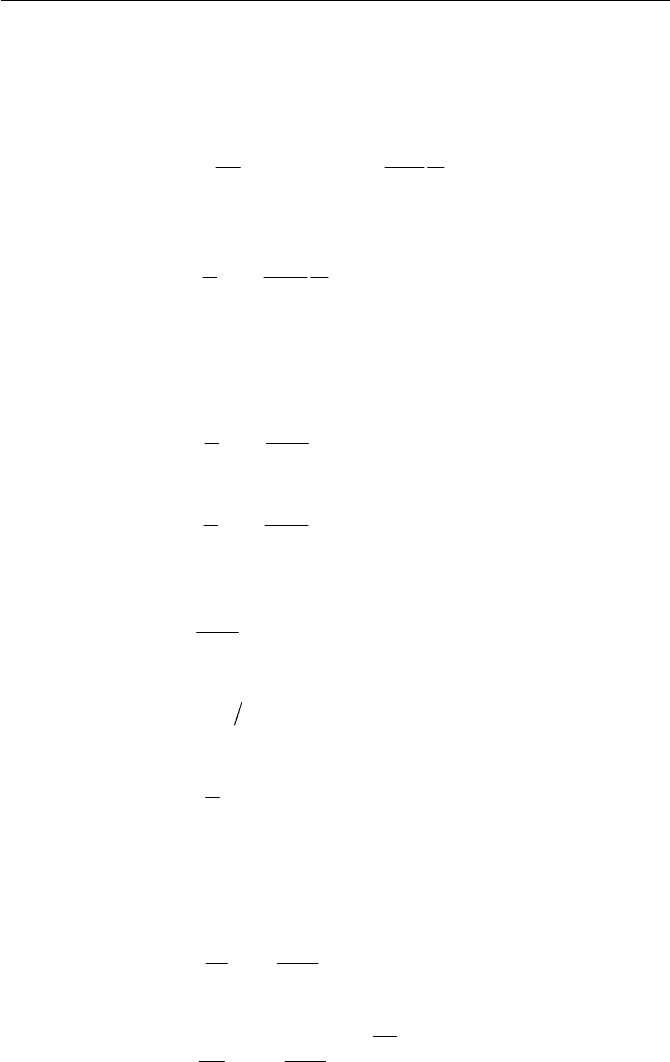
5.2 Isentropic Flow
batic, the pressure function (the second term of Eq. (5.2.7)) can be ex-
pressed in terms of the specific heat ratio
k
in the following manner, us-
ing Eq. (5.1.22)
U
UU
U
p
k
k
dkc
dp
k
1
2
0
³³
(5.2.8)
Therefore, more importantly, we discover that Eq. (5.2.7) is expressed by
.const
12
1
2
U
p
k
k
u
(5.2.9)
Equation (5.2.7) is also written in various forms, using the speed of sound
with Eq. (5.1.24) and the ideal gas relationship with Eq. (5.1.25) respec-
tively as follows
.const
12
1
2
2
k
a
u
(5.2.10)
.const
12
1
2
RT
k
k
u
(5.2.11)
and with the Mach number
const.1
2
1
2
M
k
(5.2.12)
It may prove useful to extend Eq. (5.2.12) further by recognizing that
the specific heat
1 kkRc
p
and the enthalpy
Tch
p
given in Eq.
(2.5.17), so as to write the energy equation with an equivalent form as
.const
2
1
2
hu
(5.2.13)
When we apply Eqs. (5.2.10–5.2.12) between the reservoir
0
0
u
and at an appoint
x
along the channel, subjecting to the adiabatic change
for an ideal gas, we have
2
0
2
1
1
M
k
T
T
(5.2.14)
1
2
0
2
1
1
¸
¹
·
¨
©
§
k
k
M
k
p
p
(5.2.15)
The flow is isentropic, when the thermodynamic process is kept adia-
233

5 Compressible Flow
1
1
2
0
2
1
1
¸
¹
·
¨
©
§
k
M
k
U
U
(5.2.16)
where we have used the following thermodynamic relations
1
00
¸
¹
·
¨
©
§
k
k
T
T
p
p
and
k
p
p
¸
¸
¹
·
¨
¨
©
§
U
U
00
(5.2.17)
The mass flow rate m
through the channel is expressed in the continuity
equation of Eq. (5.2.1) as
Aum
U
(5.2.18)
and
***
uAAu
UU
(5.2.19)
Note that
*
U
,
*
A
and
*
u
are the properties where the flow reaches to the
speed of sound, i.e. where the critical values at 1
M
**
au namely . As
a result of Eq. (5.2.19), we have
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
u
u
A
A
**
*
U
U
(5.2.20)
Equation (5.2.20) is another form of the continuity equation, which has to
be satisfied along the channel. This can be done with following procedure.
For
U
U
*
in Eq. (5.2.20), we can expand Eq. (5.2.16), by setting
1
M
to give
1
1
0
1
2
¸
¹
·
¨
©
§
k
k
U
U
*
(5.2.21)
so that
1
1
2
1
1
0
0
2
1
1
1
2
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
kk
M
k
k
U
U
U
U
U
U
**
(5.2.22)
Similarly for
uu
*
in Eq. (5.2.20), the critical state can be related by
the energy equation of Eq. (5.2.10), by setting
**
au
to write
234

5.2 Isentropic Flow
2
*
2
2
12
1
12
1
u
k
k
k
a
u
(5.2.23)
By dividing the both sides of this equation by
u
, we have
¸
¸
¹
·
¨
¨
©
§
2
2
2
2
12
1
1
1
2
1
u
u
k
k
u
a
k
*
(5.2.24)
and thus
2
1
2
2
11
1
1
1
12
»
¼
º
«
¬
ª
¿
¾
½
¯
®
Mkk
k
u
u
(5.2.25)
Substitution of Eqs. (5.2.22) and (5.2.25) into Eq. (5.2.20) yields the fol-
lowing relationship
12
1
2
2
1
1
1
21
¿
¾
½
¯
®
¸
¹
·
¨
©
§
k
k
M
k
kM
A
A
(5.2.26)
Equation (5.2.26) shows that
AA
becomes minimum
1
AA
for 1
M
,
while
1!
AA
for
1!
M
and
1M
. This leads the fact that for
1!
AA
there are two possible states: one is
1
M
(subsonic) and the another is
1!
M
(supersonic). Plots of
0
pp ,
AA versus
M
are displayed for
41
. k in Fig. 5.4.
The Mach number M is also eliminated by combining Eqs. (5.2.15)
and (5.2.26), yielding
»
»
»
»
¼
º
«
«
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
°
¿
°
¾
½
°
¯
°
®
¸
¸
¹
·
¨
¨
©
§
»
»
»
¼
º
«
«
«
¬
ª
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
kk
k
k
k
p
p
p
p
k
k
A
A
1
0
2
1
1
0
12
1
2
1
1
1
2
2
1
(5.2.27)
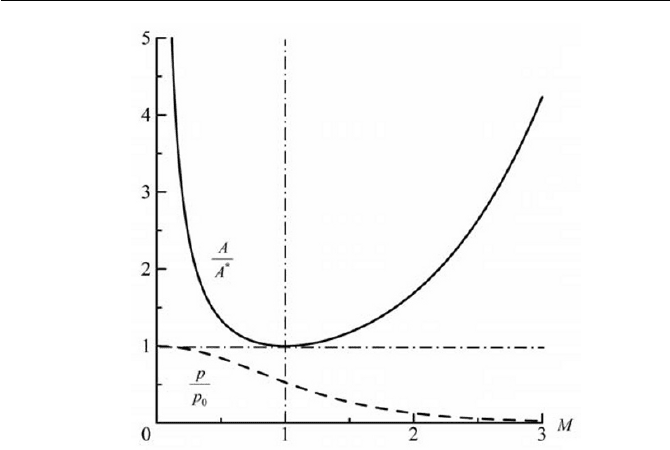
In order to make supersonic flow possible, the Laval tube is considered
as previously mentioned, taking into account the pressure variation in Eq.
(5.2.27) along the tube, where the stagnation pressure
0
p and all relevant
quantities are supposed to be given. With Eq. (5.2.27), the pressure varia-
tion
p
for the tube area A will be obtained as
A being a variable parame-
ter. The states of pressure variations are displayed in Fig. 5.5(a) and (b),
where the area of the throat is denoted as
t
A
.
235
5 Compressible Flow
Fig. 5.4 Plots of representative quantities,
4.1 k
With reference to Fig. 5.5(a), the flow regimes of those appeared
through the tube are dependent upon the pressure
e
p and the condition of
A , where
e
p is the receiver pressure that is kept constant during the de-
velopment of flow through the tube.
e
p can be altered to produce various
states of flow as schematically displayed in Fig 5.5(b). Line (1) is one that
implies
t
AA
*
, in which the flow appeared throughout the tube is kept
with a subsonic flow. The tube functions as a nozzle and a diffuser. When
e
p is further decreased with the condition of
t
AA
*
, line (2) to line (4)
appear, depending on the receiver pressure:
2e
p to
5e
p . If the receiver
pressure is reduced to
2e
p , the pressure at the throat reaches a minimum,
the critical state in which the flow reaches the speed of sound. However,
the flow in the diverging section is still subsonic.
When the receiver pressure is further reduced to
3e
p
, the flow after the
throat in some distance becomes supersonic. Then a non-isentropic flow
appears followed by a discontinuity in pressure, the normal shock, which
renders the isentropic assumption invalid. The flow will be subsonic for
the remaining distance to the exit, as indicated by line (3) in Fig. 5.5(a), and
schematically in Fig. 5.5(b). The pressure
4e
p is the condition of the shock
that exists at the exit of the Laval tube. There is a receiver pressure
5e
p
with which the flow is isentropic and supersonic in the diverging section.
The Mach number associated with
5e
p
is called the design Mach number.
236
5.2 Isentropic Flow
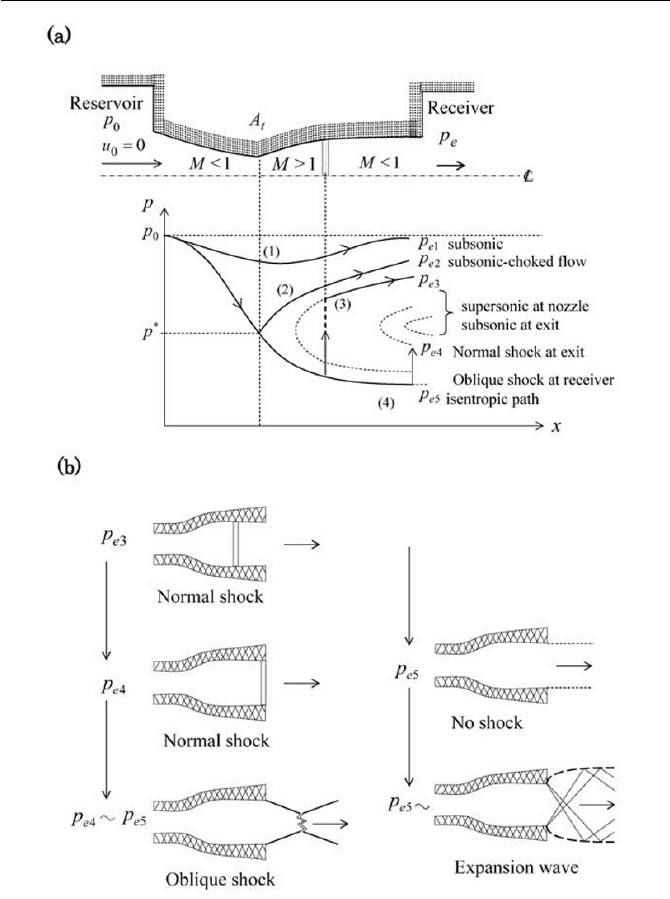
Fig. 5.5 Flow regimes of Laval tube
The pressure variation along the tube follows the isentropic path as in-
dicated in Fig. 5.5(a). Oblique shock patterns occur outside the tube (in the
receiver) due to the pressure between
4e
p ~
5e
p
, where the Laval tube is in
237
5 Compressible Flow
its so-called, over-expanded condition. As pressure
e
p approaches to
5e
p
,
the oblique shock patters tend to fade away. For the pressure below
5e
p
,
Fig. 5.5(b) represents a very complicated flow that exists outside the tube
(at the abrupt part of receiver), where expansion waves are formed.
The mass flow rate m
through the channel in Fig. 5.5(a) increases
from line (1) up to line (2). However, at the receiver pressure of
2e
p
and
that below line (2), no increase in mass flow is observed to occur, and this
situation of flow is said to be choked flow, where the Mach number at the
throat is in unity.
In order to verify the chocked flow, let us consider a simple converging
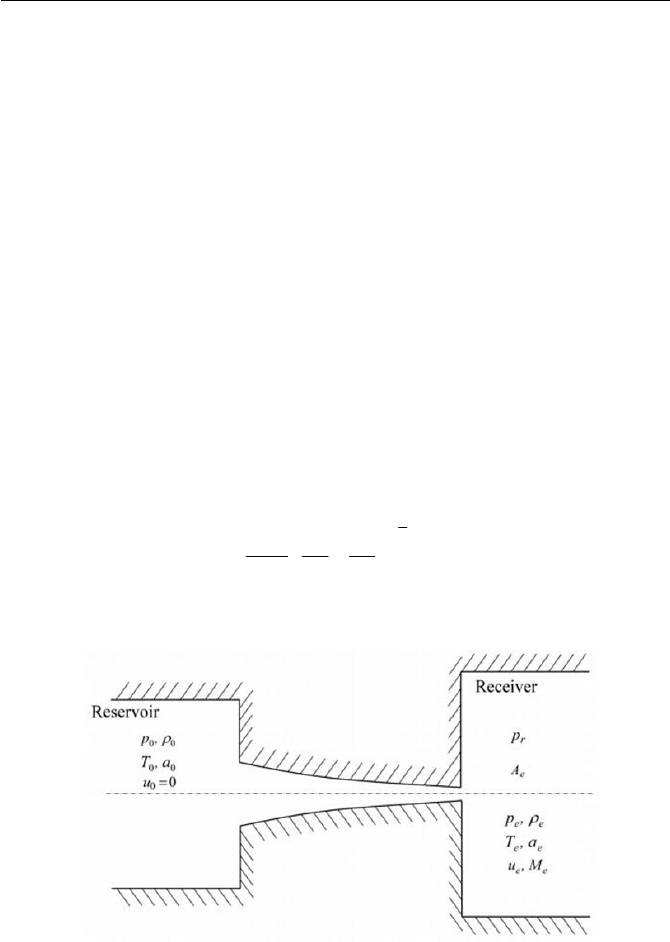
gas nozzle (as often seen on gas turbines), as shown in Fig. 5.6. The mass
flow rate m
at the exit of the nozzle can be obtained by the mass continuity
eee
Aum
U
(5.2.28)
The key to establishing a kinematic relationship between the reservoir
and receiver is achieved by setting the energy equation between the reser-
voir and the nozzle exit in Eq. (5.2.9), where we have
2
1
0
0
1
2
¿
¾
½
¯
®
¸
¸
¹
·
¨
¨
©
§
e
e
e
pp
k
k
u
UU
(
5.2.29)
Fig. 5.6 Converging nozzle
238
5.2 Isentropic Flow
so that Eq. (5.2.28) becomes
2
1
00
2
0
2
0
1
1
2
°
¿
°
¾
½
°
¯
°
®
¸
¸
¹
·
¨
¨
©
§
p
p
RTk
k
Am
eee
ee
U
U
U
U
U
(5.2.30)
Since we assume the isentropic process in the nozzle, denoting that
0
0
pp
e
k
e
UU
in Eq. (5.2.17), we can write Eq. (5.2.30) in the follow-
ing form
2
1
1
0
2
00
0
1
1
2
»
»
»
¼
º
«
«
«
¬
ª
°
¿
°
¾
½
°
¯
°
®
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
k
k
e
k
e
e
p
p
p
p
RTk
k
pAm
(5.2.31)
Equation (5.2.31) indicates that, if we take the receiver conditions as fixed,
the mass flow rate m
only function as
e
p for a given
e
A . The plotted line
in Fig. 5.7 is a curve of Eq. (5.2.31). In actual flow, there is some discrep-
ancy between Eq. (5.2.31) and reality, as indicated in Fig. 5.7 by a solid
line. By differentiating Eq. (5.2.31) in terms of
0
pp
e
and setting the re-
sult equal to zero, we found the maximum of
max
m
and its corresponding
pressure
0
pp
c
;
k
k
c
k
p
p
¸
¹
·
¨
©
§
1
0
2
1
(5.2.32)
where
c
p is called the critical pressure. It is mentioned that experiments
show that the nozzle exist (the throat) pressure
e
p is never less than the
value for the actual maximum pressure. As this is indicated in Fig. 5.7 by
the solid line, if the receiver pressure
r
p is reduced below
c
p , the mass
flow rate
m
will not increase, where the condition of choked flow occurs.
Upon the condition of choked flow, the mass flow remains at the maxi-
mum value and on the exist of the converging nozzle (Fig. 5.6) the fluid
undergoes an unrestrained and irreversible expansion to
e
p
. In practice the
flow becomes no longer amendable to simple one dimensional treatment
after the onset of the choking condition.
In order to derive an equation of mass flow rate
m
in terms of Mach
number, the terms containing
0
pp
e
in Eq. (5.2.31) are eliminated with
the aid of Eq. (5.2.15), thereby giving
239
5 Compressible Flow
Fig. 5.7 Mass flow rate for variation of
e
p
k
k
e
M
k
M
RT
k
pAm
¸
¹
·
¨
©
§
12
1
2
0
0
2
1
1
(5.2.33)
If we choose the critical area
*
A
for
1
*
M
, we have
k
k
k
RT
k
pAm
¸
¹
·
¨
©
§
12
1
0
0
max
2
1
*
(5.2.34)
or
k
k
k
kpAm
¸
¹
·
¨
©
§
12
1
00
max
2
1
U
*
(5.2.35)
Thus, the mass flow rate is only dependent upon the reservoir condition
and the throat area
A . For air, the critical pressure ratio corresponding to
240

5.3 Fanno and Rayleigh Lines
4.1 k can be calculated from Eq. (5.2.32) to give
528.0
0
pp
c
, and
the maximum flow rate at the chocking condition will be given as
0
0
max
6850
U
pAm
*
.
(5.2.36)
Therefore, further reduction of
r
p in a receiver below
c
p results in no ef-
fect on the upstream, since any disturbances caused in the receiver do not
travel upstream in the nozzle throat where the Mach number is kept 1. In
order to increase the Mach number above its unity through the channel, a
diverging section is needed to the converging nozzle section, forming the
Laval tube previously discussed.
5.3 Fanno and Rayleigh Lines
There are some flows through a pipe that have friction, whereas the ther-
modynamic state is kept as isothermal. The situation is often encountered
in a gas form, for example natural gas, in a long pipeline. We will treat this
problem for an ideal gas in constant cross section channels, where the flow
is assumed to be one dimensional and steady. The thermodynamic behav-
ior of such a flow can be obtained by considering a diagram of enthalpy
h
(or temperature
T
) versus entropy
s
. In analyzing a chocked flow and
shock wave characteristics, the Fanno and Rayleigh lines (curves) plotted
on the enthalpy
h – entropy
s
diagram are useful in consideration of a
graphical interpretation of the process.
The equations of the Fanno line are derived from the mass continuity,
the energy equation and the thermodynamic relations between the stagna-
tion condition and a point in the channel, as long as the channel section is
kept adiabatic regardless of the friction.
In Eq. (5.2.18) where
.const A , the continuity equation is written as
const.
uG
U
(5.3.1)
where G is the mass flux. The energy equation of Eq. (5.2.13) is written
for an ideal gas, i.e.
Tch
p
, as
0
2
2
1
hhu
(5.3.2)
The thermodynamic relations, Eq. (2.5.6) and Eqs. (2.5.15–2.5.17),
with the adiabatic process, i.e.
.const1
k
p
U
, are given in terms of the
entropy change as follows
241

5 Compressible Flow
°
¿
°
¾
½
°
¯
°
®
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
P
p
T
T
Rss
k
1
1
1
1
1
ln
(5.3.3)
and
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
1
1
1
1
ln
k
v
P
p
h
h
css
(5.3.4)
where
(1)
suffix is the reference state point with known values of enthalpy
1
h , entropy
1
s , density
1
U
and temperature
1
T on the
sh
diagram.
In Eqs. (5.3.1–5.3.4), the stagnation condition is defined for the enthalpy
0
h , while at an arbitrary point in the channel the quantities are defined
without suffix. Combining Eqs. (5.3.1) and (5.3.2), we can write Eq.
(5.3.4) as the relation between the enthalpy and the entropy as
°
¿
°
¾
½
°
¯
°
®
¸
¸
¹
·
¨
¨
©
§
2
1
0
1
1
1
1
2
ln
k
k
v
hh
h
h
G
css
U
(5.3.5)
Further simplified, we can say
°
¿
°
¾
½
°
¯
°
®
2
1
101
2
1
0
1
ln
k
k
v
hhh
hhh
css
(5.3.6)
Some simplifications are expressed in Eq. (5.3.6), and it maybe written for
h as follows
¸
¸
¹
·
¨
¨
©
§
s
c
k
k
k
p
eGChhh
1
1
2
1
0
(5.3.7)
where
1
C is a constant defined as state point (1) in the sh diagram and
is calculated with
1
G ,
1
h and
1
s .
The line of either Eqs. (5.3.6) or (5.3.7) drawn in the
sh
diagram is
labeled as the Fanno line (or Fanno curve). The Fanno lines given by the
function of Eqs. (5.3.6) or (5.3.7) are plotted exaggeratingly in Fig. 5.8(a)
and (b) respectively. We can find that
s
reaches a maximum when
s
in Eq.
(5.3.6) is differentiated with respect to
h and setting dhds to zero, i.e.
242
