Xing Zh., Zhou Sh. Neutrinos in Particle Physics, Astronomy and Cosmology
Подождите немного. Документ загружается.

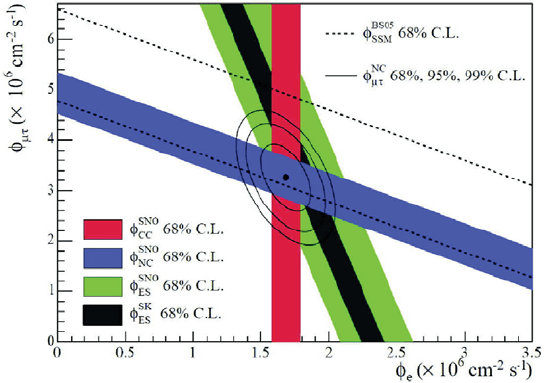
66 3 Neutrinos beyond the
S
tandard Mode
l
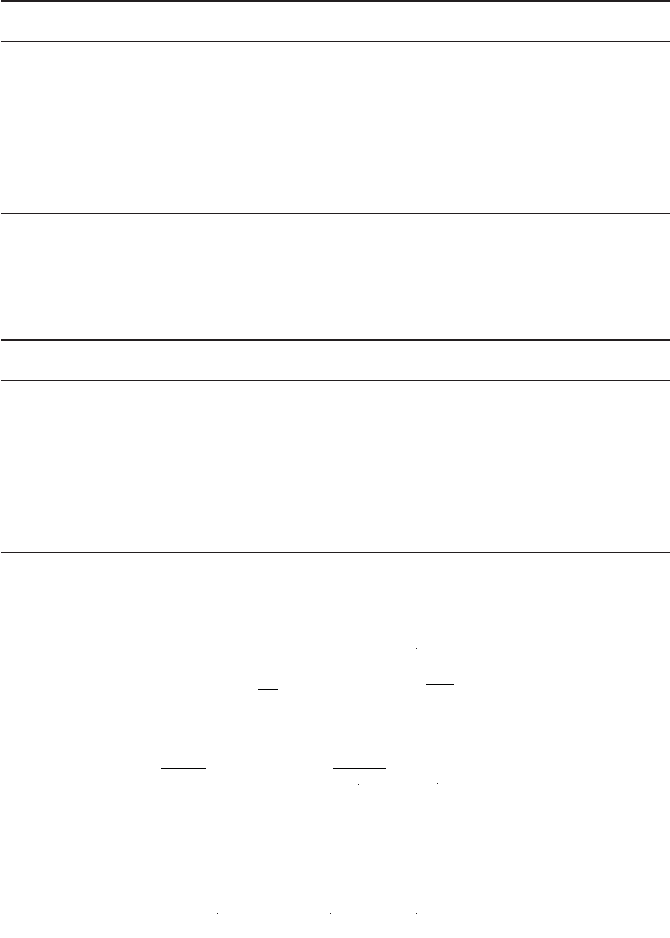
Fi
g
.3.3 T
he
ν
μ
+
ν
τ
fl
ux versus the
ν
e
fl
ux determined
f
rom the
S
N
O
data. Th
e
total
8
B solar neutrino flux predicted by the SSM is shown as dashed lines, parallel
to the N
C
measurement. The narrow band
p
arallel to the
S
N
O
’s E
S
measurement
corresponds to the
S
K’s E
S
result. The best-
fi
t point is obtained usin
g
only the
SNO data
(
Aharmim
et al
., 2005. With permission from the American Physica
l
Society
)
w
h
e
r
e
σ
μ
/
σ
e
≈
0
.
155 is the ratio o
f
elasti
c
ν
μ
-
e
a
n
d
ν
e
-
e
scatter
i
n
g
cross
-
s
ections
,
an
d
φ
μ
τ
d
enotes the flux of active non-electron neutrinos. Of course
,
φ
μτ
=
0 or equiva
l
ent
l
y
φ
CC
=
φ
NC
=
φ
E
S
would hold, i
f
there were no
fl
avor
c
onversion. The SNO data yield
(
Aharmim
et al.
,
2005
)
φ
CC
=
1.
68
+0
.
06
−
0
.
06
(
stat.
)
+
0
.
08
−
0
.
09
(
syst.
)
,
φ
ES
=2
.
35
+0
.
22
−
0
.
22
(
stat.
)
+
0
.
15
−
0
.
1
5
(
syst.
)
,
φ
N
C
=4
.
94
+0
.
21
−
0
.
21
(
stat.
)
+
0
.
38
−
0
.
34
(
syst.
)
,
(
3.4
)
f
rom which the
fl
avor composition o
f
8
B sola
rn
eut
rin
os
i
sdete
rmin
ed a
n
d
s
ummarized in Fi
g
. 3.3. This impressive result is consistent with the SS
M
prediction
(
Bahcall
e
ta
l.
,
2005
)
and indicates the existence o
f
ν
μ
a
n
d
ν
τ
neut
rin
os
in
t
h
eflu
x
of so
l
a
rn
eut
rin
os o
n
to t
h
e
E
a
r
t
h
.
T
he flavor conversion of sola
r
8
B neutrinos, whose typical ener
g
ies ar
e
ab
out6MeVto7MeV,ismost
l
i
k
e
l
y
d
ue t
o
ν
e
→
ν
μ
osc
i
llat
i
o
n
sassoc
i
ated
with the Mikheyev-Smirnov-Wolfenstein
(
MSW
)
matter effects
(
Wolfenstein,
1
978; Mikheyev and Smirnov, 1985
)
. Before the KamLAND reactor neutrino
experiment
(
Eguchi
et al.
,
2003
)
, a global analysis of all available experi
-
m
ental data on solar neutrinos
(
in particular, those from the SK and SNO
m
easurements
)
in the two-flavor oscillation scheme led to several allowed re-
3.1 Experimental Evidence
f
or Neutrino Masses 6
7
θ
!
"
#
Δ
Fig. 3.4 Allowed region for two-flavor neutrino oscillation parameters from the
solar neutrino and KamLAND experiments
(
Ab
e
et al
.
,
2008. Wit
hp
ermission
from the American Physical Society
)
g
ions o
f
Δ
m
2
a
n
dta
n
2
θ
:
the SMA
(
small mixing angle
)
,LMA
(
large mixin
g
a
ngle
)
and LOW
(
low mass-squared difference
)
regions based on the MS
W
m
echanism as well as the VO
(
vacuum oscillation
)
and other possible regions
.
It was the KamL
A
ND measurement that sin
g
led out the LM
A
MSW solutio
n
a
s the onl
y
acceptable solution to the solar neutrino problem
.
Note also that the Borexino experiment
(
Arpesell
a
et al
., 2008a; 2008b
)
h
as provided the
fi
rst real-time detection o
f
the mono-ener
g
etic solar
7
B
e
n
eu
-
trinos wit
h
E
=
0
.
8
62 MeV and observed a remarkable deficit correspondin
g
to
P
(
ν
e
→
ν
e
)
=0
.
56
±
0
.
1
.T
h
is resu
l
tcan
b
e interprete
d
a
s
ν
e
→
ν
μ
osc
i
lla-
tions in vacuum, as the matter e
ff
ects on low-ener
gy
7
Be
n
eut
rin
oosc
i
llat
i
o
n
s
a
re fairly insignificant
(
Kayser, 2008
)
. More accurate measurements o
f
7
B
e
-
assoc
i
ated
ν
e
events will be very important
f
or much better understandin
g
o
f
the interpla
y
between solar neutrino oscillations and M
S
W matter e
ff
ects.
3.1.4 Reactor Neutrino
O
scillations
The KamLAND Collaboration has measured the partial disappearance o
f
ν
e
e
vents, which were ori
g
inally produced
f
rom distant nuclear reactors, by
m
eans of the inverse
β
-
deca
y
reaction ν
e
+
p
→
e
+
+
n
(
Eguch
i
e
tal.
,
2003
;
Abe
et al
.
,
2008
)
. The typical baseline of this experiment is 180 km, allowing
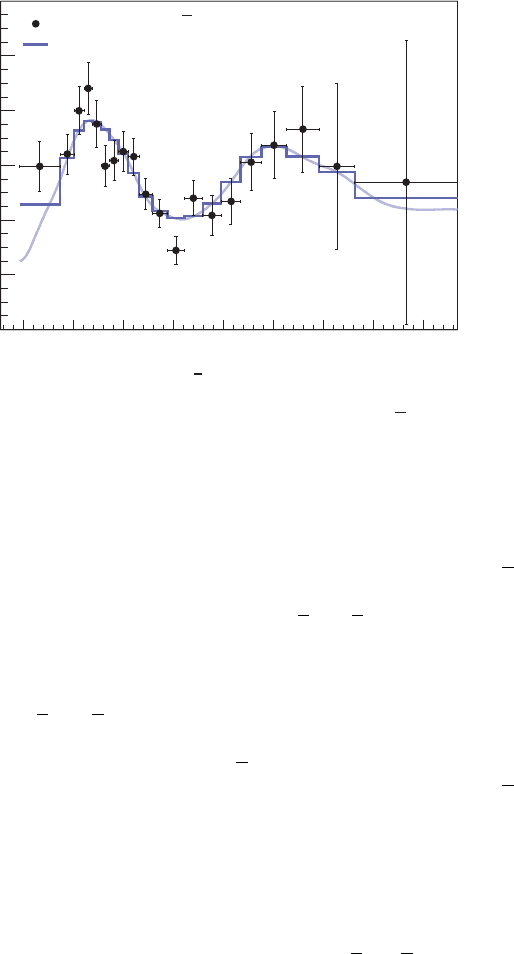
68 3 Neutrinos beyond the
S
tandard Mode
l
"$
%
&#
!
ν
%'
%
()
*+
+
,
-
(
)
ν
.//
'
012
3
2
1
3 3
-
Fi
g
. 3.5 Ratio o
f
the back
g
round and
g
eoneutrino-subtracte
d
ν
e
sp
ec
t
rum
to
the no-oscillation ex
p
ectation as a
f
unction o
f
L
0
/E
,
w
h
ere
L
0
= 180
k
mist
he
effective KamLAND baseline taken as a flux-weighted average (Abe et a
l
.
,
2008.
With permission from the American Physical Society
)
a
terrestrial test of the LM
A
solution to the solar neutrino
p
roblem. The ratio
of the observed inverse
β
-
decay events to the expected number without
ν
e
d
isappearance turns out to be convincin
g
ly smaller than one.
S
uch a de
fi
cit
c
an naturall
y
be interpreted in the h
y
pothesis of
ν
e
→
ν
μ
o
scillations
,
and
t
h
e correspon
d
ing parameter space s
h
own in Fig. 3.4 is compati
bl
everywe
ll
with the LM
A
re
g
ionofsola
r
ν
e
→
ν
μ
oscillations under
C
PT invarianc
e
(
Abe
et al
.
,
2008
)
:
Δ
m
2
=(7
.
59
±
0
.
21
)
×
10
−
5
e
V
2
a
n
dta
n
2
θ
=0
.
4
7
+
0
.
06
−
0
.
05
.
I
n
p
articular
,
P
(
ν
e
→
ν
e
)
measured in the KamLAND experiment dis
-
plays a striking sinusoidal behavior of two-flavor oscillations
(
see Fig. 3.5
).
Note t
h
at t
h
e
K
a
mL
A
ND
detecto
r
detects
ν
e
events comin
gf
rom a number
of reactors at different distances
,
so the distance
L
travelled by any give
n
ν
e
i
s unknown
(
Kayser, 2008
)
. For this reason, Fig. 3.5 plots the experimenta
l
data ve
r
sus
L
0
/E
w
i
th
L
0
=
180 km bein
g
a
fl
ux-wei
g
hted avera
g
edistance
.
The oscillatory curve and histogram in this figure have taken account of the
a
ctual distances to the individual reactors.
O
ne can see almost two c
y
cles o
f
the sinusoidal structure of neutrino oscillations
.
T
he CHOOZ
(
Apollonio
e
ta
l
., 1998
)
and Palo Verde
(
Boeh
m
et a
l.
,
2000
)
reactor antineutrino experiments were done to search
f
or
ν
e
→
ν
e
osc
i
llat
i
o
n
s
i
n the atmospheric ran
g
eo
f
Δ
m
2
. No indication in favor of neutrino oscilla
-
tions was found from both experiments, leading to a strong constraint on the
s
ma
ll
est neutrino mixin
g
an
gl
e: sin
2
2
θ
c
hz
<
0
.
10
f
or
Δ
m
2
chz
>
3
.
5
×
10
−
3
e
V
2
;
or s
in
2
2
θ
chz
<
0
.
1
8for
Δ
m
2
c
h
z
>
2
.
0
×
1
0
−
3
eV
2
.
3.2 Dirac an
d
Majorana Neutrino Mass Terms 6
9
3.1.5 Implications of Experimental Data
The neutrino experiments that we have briefl
y
summarized involve differen
t
n
eutrino sources, different neutrino flavors, different neutrino beam energies
a
nd
(
or
)
different neutrino travel distances. But the observed neutrino deficit
s
c
an all be explained in the framework of three-flavor oscillations, onl
y
if three
k
nown neutrinos
h
ave non-
d
egenerate masses an
d
nontrivia
l
mixing ang
l
es
.
S
uch a solution is natural and economical in the sense that it does not invoke
a
ny
(
exotic
)
new particles or new forces, or change the SSM, or fine-tun
e
the parameter space
(
Xing, 2008a
)
. We conclude that neutrino oscillations
h
ave de
fi
nitely been observed, implyin
g
that at least two neutrinos must
bemassive.Thisistheonl
y
new ph
y
sics be
y
ond the SM which has bee
n
established on solid experimental ground in the past four decades
.
Ag
lobal three-flavor analysis of all the available experimental data o
n
s
olar
(
SNO, SK, Borexino
)
, atmospheric
(
SK
)
, reactor
(
KamLAND and
CHOOZ
)
and accelerator
(
K2K and MINOS
)
neutrino oscillations has bee
n
d
one by two different groups
(
Schwet
z
et al.
,
2008; Fo
g
li
et al
.
,
2008a
)
. Tables
3
.1 and 3.2 list their main results for two neutrino mass-s
q
uared differences
a
nd three neutrino mixin
g
an
g
les, respectively.
O
ne can see that the numer
-
i
cal results of these two anal
y
ses are essentiall
y
compatible with each other.
A
lthough si
n
2
θ
13
=0
.
016
±
0
.
010
(
1
σ
)
is claimed to be an interesting hint a
t
θ
1
3
>
0(
Fogli
et al
., 2008b
)
, its significance remains quite poor
.
O
nl
y
some upper bounds on the absolute neutrino mass scale have bee
n
obtained from current data on the beta decay, the neutrinoless double-beta
(0
ν
2
β
)
decay and cosmology
(
Strumia and Vissani, 2006; Selja
k
et al.
,
2006
).
The following statements should be true:
(
a
)
every neutrino mass must b
e
below
O
(
1
)
eV;
(
b
)
one neutrino mass must be larger than
|
Δ
m
2
3
1
|∼
0
.
05
eV; and
(
c
)
the smallest neutrino mass can be zero. The origin of finit
e
n
eutrino masses demands a kind of new ph
y
sics be
y
ond the SM
.
3
.2 D
i
rac and Ma
j
orana Neutr
i
no Mass Term
s
To write out the mass term for three known neutrinos
,
let us make a minimal
extension o
f
the
S
M by introducin
g
three ri
g
ht-handed neutrinos. Then w
e
totall
y
have six neutrino field
s
2
:
ν
L
=
⎛
⎝
⎛⎛
ν
e
L
ν
μ
L
ν
τ
L
⎞
⎠
⎞⎞
,N
R
NN
=
⎛
⎝
⎛⎛
N
1R
NN
N
2R
NN
N
3R
NN
⎞
⎠
⎞⎞
,
(
3.5
)
2
T
he left- and right-handed components of a fermion field ψ
(
x
)
are denoted a
s
ψ
L
(
x
)
=
P
L
PP
ψ
(
x
)
and
ψ
R
(
x
)
=
P
R
PP
ψ
(
x
)
, respectively, where
P
L
PP
≡
(1
−
γ
5
)
/
2
a
n
d
P
R
P
P
≡
(
1+
γ
5
)
/
2 are t
h
ec
h
ira
l
pro
j
ection operators. Note,
h
owever, t
h
a
t
ν
L
=
P
L
P
P
ν
L
an
d
N
R
N
N
=
P
R
P
P
N
R
N
N
a
re in general independent of each other.
70 3 Neutrinos beyond the
S
tandard Mode
l
Table
3
.1 Best-fit values with
1
σ
errors together with
2
σ
a
nd
3
σ
i
n
te
r
va
l
s
f
or
three-
fl
avor neutrino oscillation parameters
f
rom a
g
lobal analysis o
f
current data
(
Schwet
z
e
ta
l.
,
2008. With permission from the Institute of Physics
)
.Here
Δ
m
2
21
≡
m
2
2
−
m
2
1
a
n
d
Δ
m
2
31
≡
m
2
3
−
m
2
1
a
r
ede
fin
ed
P
arameter Best fit +
1
σ
2
σ
3
σ
Δ
m
2
21
10
−
5
eV
2
7
.
6
5
+
0
.
23
−
0
.
2
0
7.25 to 8.11 7.05 to 8.34
Δ
m
2
31
10
−
3
eV
2
2
.
40
+
0
.
12
−
0
.
11
2
.18to2.6
4
2.07 to 2.7
5
s
i
n
2
θ
1
2
0
.
304
+0
.
022
−
0
.
016
0
.2
7
to
0
.
35 0
.2
5
to
0
.
37
si
n
2
θ
23
0
.
50
+0
.
0
7
−
0
.
06
0
.
39
to
0
.
63 0
.
36
to
0
.
67
sin
2
θ
13
0
.
01
+0
.
0
1
6
−
0
.
011
0
.0
4
0
0.05
6
Table 3.2 Best-
fi
t values and allowed
1
σ
,2
σ
a
n
d
3
σ
ran
g
es
f
or three-
fl
avor neutrin
o
oscillation parameters from a global analysis of current data (Fogli et a
l.
,
2008a
.
With permission from the American Physical Society
)
.Her
e
δ
m
2
≡
m
2
2
−
m
2
1
a
n
d
Δ
m
2
≡
|
m
2
3
−
(
m
2
1
+
m
2
2
)
/
2
|
a
re de
fi
ne
d
P
a
r
a
m
ete
rB
est fit 1
σ
2
σ
3
σ
δm
2
10
−
5
eV
2
7
.
67 7
.
48
to
7
.
83 7
.
3
1to
8
.
0
1
7
.1
4
to
8
.1
9
Δ
m
2
10
−
3
eV
2
2
.
39 2
.
31
to
2
.
50 2
.
19
to
2
.
66 2
.
06
to
2
.
81
sin
2
θ
12
0.312 0.294 to 0.331 0.278 to 0.352 0.263 to 0.375
sin
2
θ
23
0.
4
66 0.
4
08 to 0.539 0.366 to 0.602 0.331 to 0.6
44
s
i
n
2
θ
13
0
.
016 0
.
006
to
0
.
026
<
0
.
036
<
0
.
0
4
6
where only the le
f
t-handed
fi
elds take part in the electroweak interactions.
The char
g
e-conju
g
ate counterparts o
f
ν
L
a
n
d
N
R
NN
a
r
edefi
n
ed as
(
ν
L
)
c
≡
C
ν
L
T
,
(
N
R
NN
)
c
≡C
N
R
NN
T
;
(
3.6
)
a
n
d
accor
d
ing
l
y,
(
ν
L
)
c
=(
ν
L
)
T
C
,
(
N
R
NN
)
c
=
(
N
R
NN
)
T
C
,
(
3.7
)
where
C
denotes the char
g
e-conju
g
ation matrix and satisfies the conditions
C
γ
T
μ
C
−
1
=
−
γ
μ
,
C
γ
T
5
C
−
1
=
γ
5
,
C
−
1
=
C
†
=
C
T
=
−
C
.
(
3.8
)
It is easy to c
h
ec
k
t
h
a
t
P
L
PP
(
N
R
NN
)
c
=
(
N
R
NN
)
c
a
n
d
P
R
PP
(
ν
L
)
c
=
(
ν
L
)
c
h
o
ld
; name
l
y,
(
ν
L
)
c
=
(
ν
c
)
R
a
nd
(
N
R
NN
)
c
=
(
N
c
)
L
hold. Hence
(
ν
L
)
c
a
nd
(
N
R
NN
)
c
are ri
g
ht
-
a
nd left-handed fields, respectively. One may then use the neutrino field
s
ν
L
,

3.2 Dirac an
d
Majorana Neutrino Mass Terms 71
N
R
N
N
an
d
t
h
eir c
h
ar
g
e-conju
g
ate partners to write out t
h
e
g
au
g
e-invariant an
d
L
orentz-invariant neutrino mass terms.
I
n the SM the weak charged-current interactions of three active neutrinos
a
re
g
iven
by
L
c
c
=
g
√
2
(
eμτ
)
L
γ
μ
⎛
⎝
⎛⎛
ν
e
ν
μ
ν
τ
⎞
⎠
⎞⎞
L
W
−
μ
W
+h
.
c
..
(
3.9
)
Without loss of generality, we choose the basis in which the mass eigen
-
s
tates o
f
three char
g
ed leptons are identi
fi
ed with their
fl
avor ei
g
enstates
.
If neutrinos have nonzero and non-degenerate masses, their flavor and mass
ei
g
enstates are in
g
enera
l
not i
d
entica
l
in t
h
ec
h
osen
b
asis. T
h
is mismatc
h
s
ignifies the phenomenon of lepton flavor mixing
(
Maki
et al.
,
1962
).
3.2.1 Dirac Masses and Le
p
ton Number
C
onservation
A
Dirac neutrino is described by a four-component Dirac spino
r
ν
=
ν
L
+
N
R
NN
,
whose le
f
t-handed and ri
g
ht-handed components are jus
t
ν
L
a
n
d
N
R
NN
.T
he
D
irac neutrino mass term comes from the Yukawa interactions
−
L
D
ir
ac
=
L
Y
ν
YY
˜
HN
R
NN
+h
.
c
.
,
(
3.10
)
whe
r
e
˜
H
≡
i
σ
2
H
∗
w
i
th
H
b
eing the SM Higgs doublet, and
L
de
n
otes the
l
eft-handed lepton doublet. After spontaneous gauge symmetry breaking
(
i.e.,
SU
(
2
)
L
×
U
(
1
)
Y
→
U
(
1
)
Q
)
, we obtain
−
L
D
irac
=
ν
L
M
D
M
M
N
R
NN
+
h
.
c
.,
(
3.11
)
where
M
D
MM
=
Y
ν
Y
Y
H
wit
h
H
174 GeV being the vacuum expectation valu
e
of
H
. This mass matrix can be diagonalized by a bi-unitary transformation:
V
†
M
D
MM
U
=
$
M
ν
MM
≡
D
ia
g
{
m
1
,
m
2
,
m
3
}
w
i
th
m
i
b
eing the neutrino masses
(
fo
r
i
=1
,
2
,
3)
. After this diagonalization, Eq.
(
3.11
)
become
s
−L
D
ira
c
=
ν
L
$
M
ν
MM
N
R
NN
+
h
.
c
.,
(
3.12
)
where
ν
L
=
V
†
ν
L
a
n
d
N
R
NN
=
U
†
N
R
NN
. Then the four-com
p
onent Dirac s
p
inor
ν
=
ν
L
+
N
R
NN
=
⎛
⎝
⎛⎛
ν
1
ν
2
ν
3
⎞
⎠
⎞⎞
,
(
3.13
)
which automatically satis
fi
e
s
P
L
PP
ν
=
ν
L
a
n
d
P
R
P
P
ν
=
N
R
N
N
,d
escri
b
es t
h
emas
s
ei
g
enstates o
f
three Dirac neutrinos. In other words
,
−L
Dir
ac
=
ν
$
M
ν
MM
ν
=
3
i
=1
m
i
ν
i
ν
i
.
(
3.14
)

72 3 Neutrinos beyond the
S
tandard Mode
l
Th
e
kin
et
i
cte
rm
of
Dir
ac
n
eut
rin
os tu
rn
souttobe
L
kinetic
=i
ν
L
γ
μ
∂
μ
ν
L
+i
N
R
NN
γ
μ
∂
μ
N
R
NN
=
i
ν
γ
μ
∂
μ
ν
=i
3
k
=
1
ν
k
γ
μ
∂
μ
ν
k
,
(
3.15
)
w
h
ere
V
†
V
=
VV
†
=
1
an
d
U
†
U
=
UU
†
=
1
h
ave
b
een use
d
.
Now we rewrite the weak char
g
ed-current interactions o
f
three neutrinos
i
nEq.
(
3.9
)
in terms of their mass eigenstates
ν
L
=
V
†
ν
L
in the chosen basis
where the flavor and mass eigenstates of three charged leptons are identical
:
L
cc
=
g
√
2
(
eμ
τ
)
L
γ
μ
V
⎛
⎝
⎛⎛
ν
1
ν
2
ν
3
⎞
⎠
⎞⎞
L
W
−
μ
W
+h
.
c
..
(
3.16
)
T
h
e3
×
3
un
i
tar
y
matr
ix
V ,w
h
ic
h
actua
ll
y
l
in
k
st
h
eneutrinomassei
g
enstate
s
(
ν
1
,
ν
2
,ν
3
)
to the neutrino flavor eigenstates
(
ν
e
,
ν
μ
,ν
τ
)
, just measures the
phenomenon of neutrino mixing
.
A
salient feature of massive Dirac neutrinos is lepton number conser
-
vation. Table 3.3 lists the le
p
ton number
L
a
nd the lepton flavor
(
family
)
nu
m
ber
L
α
o
f
every lepton in the
S
M. To see why massive Dirac neutrinos
a
re lepton-number-conservin
g
,wemakethe
g
lobal phase trans
f
ormations
l
(
x
)
→
e
i
Φ
l
(
x
)
,ν
L
(
x
)
→
e
i
Φ
ν
L
(
x
)
,N
R
NN
(
x
)
→
e
i
Φ
N
R
NN
(
x
)
,
(
3.17
)
where
l
denotes the column vector of
e
,
μ
an
d
τ
fi
elds
,
and
Φ
is an arbitrary
s
pacetime-in
d
epen
d
ent p
h
ase. Because t
h
e mass term
L
D
ira
c
,
t
h
e
k
inetic ter
m
L
k
ineti
c
and the char
g
ed-current interaction term
L
cc
a
r
ea
ll in
va
ri
a
n
tu
n
-
d
er these transformations, the le
p
ton number must be conserved for massiv
e
D
irac neutrinos. It is evident that lepton
fl
avors are violated, unless
M
D
MM
is d
i-
ag
onal or equivalently V
i
stheidentit
y
matrix. In other words, lepton flavo
r
m
ixing leads to lepton flavor violation, or vice versa.
Ta
bl
e3.3 Le
p
ton num
b
er
L
and lepton flavor
(
family
)
number
L
α
o
f
char
g
ed
leptons and neutrinos
(
fo
r
α
=
e
,
μ
,τ
)
in the SM
e
−
ν
e
e
+
ν
e
μ
−
ν
μ
μ
+
ν
μ
τ
−
ν
τ
τ
+
ν
τ
L
+
1
+1
−
1
−
1
+
1
+1
−
1
−
1+
1
+1
−
1
−
1
L
e
+
1
+1
−
1
−
100000000
L
μ
0000
+
1
+
1
−
1
−
1
000
0
L
τ
00000000
+
1
+1
−
1
−
1
For example, the deca
y
mode π
−
→
μ
−
+
ν
μ
p
reserves both the le
p
ton
n
umber and le
p
ton flavors. In contrast
,
μ
+
→
e
+
+
γ
p
reserves the le
p
ton

3.2 Dirac an
d
Majorana Neutrino Mass Terms 7
3
n
umber but violates the lepton
fl
avors. The observed phenomena o
f
neutrino
oscillations verif
y
the existence of neutrino flavor violation. Note that the
0
ν
2
β
d
ecay
(
A, Z
)
→
(
A
,
Z
+
2
)
+
2
e
−
v
io
l
ates t
h
e
l
epton num
b
er. T
h
i
s
process cannot take place i
f
neutrinos are massive Dirac particles, but it ma
y
n
aturall
y
happen if neutrinos are massive Ma
j
orana particles
.
3.2.2 Ma
j
orana Masses and Lepton Number Violatio
n
Th
e
l
eft
-h
a
n
ded
n
eut
rin
ofie
l
d
ν
L
a
nd its charge-conjugate counterpart
(
ν
L
)
c
c
an in principle form a neutrino mass term, as
(
ν
L
)
c
i
s actually ri
g
ht-handed.
But this Majorana mass term is forbidden by the
SU
(
2
)
L
×
U
(
1
)
Y
gauge
s
ymmetry in the
S
M, which contains only one
SU
(
2
)
L
Hi
gg
s
d
ou
bl
et an
d
p
reserves le
p
ton number conservation. We shall show in Section 4.1.2 tha
t
the introduction of a
n
SU
(
2
)
L
Higgs triplet into the SM can accommodate
s
uc
h
aneutrinomasstermwit
hg
au
g
e invariance. Here we i
g
nore t
h
e
d
etai
l
s
of the Hi
gg
s triplet models and focus on the Majorana neutrino mass ter
m
i
tself
(
Gribov and Pontecorvo, 1969
)
:
−
L
M
a
j
oran
a
=
1
2
ν
L
M
L
MM
(
ν
L
)
c
+h
.
c
..
(
3.18
)
Note that the
m
ass
m
at
ri
x
M
L
MM
m
ust
b
es
y
mmetric. Because t
h
emasster
m
i
s a Lorentz scalar whose transpose keeps unchan
g
ed, we have
ν
L
M
L
M
M
(
ν
L
)
c
=
[
ν
L
M
L
M
M
(
ν
L
)
c
]
T
=
−
ν
L
C
T
M
T
L
MM
ν
L
T
=
ν
L
M
T
L
MM
(
ν
L
)
c
,
(
3.19
)
where a minus si
g
n appears when interchan
g
in
g
two
f
ermion
fi
eld opera
-
tors
,
and
C
T
=
−C
h
as been used. Henc
e
M
T
L
MM
=
M
L
MM
holds. This s
y
mmetri
c
m
ass matrix can be dia
g
onalized by the trans
f
ormatio
n
V
†
M
L
MM
V
∗
=
$
M
ν
MM
≡
D
ia
g
{
m
1
,
m
2
,m
3
}
,
where
V
i
saun
i
tar
y
matr
ix
3
.
A
fter this dia
g
onalization,
E
q.
(
3.18
)
become
s
−
L
M
a
j
oran
a
=
1
2
ν
L
$
M
ν
MM
(
ν
L
)
c
+h
.
c
.,
(
3.20
)
where
ν
L
=
V
†
ν
L
a
nd
(
ν
L
)
c
=
C
ν
L
T
. Then the fiel
d
ν
=
ν
L
+(
ν
L
)
c
=
⎛
⎝
⎛⎛
ν
1
ν
2
ν
3
⎞
⎠
⎞⎞
,
(
3.21
)
which satisfies the Majorana condition
(
ν
)
c
=
ν
(
Majorana, 1937
)
, describe
s
the mass eigenstates of three Majorana neutrinos. In other words,
3
A
proof of this theorem is very easy
(
see, e.g., Bilenky and Petcov, 1987; Dreiner
e
ta
l
.
,
2008; and references therein)
.

74 3 Neutrinos beyond the
S
tandard Mode
l
−L
M
ajoran
a
=
1
2
ν
$
M
ν
MM
ν
=
1
2
3
i=1
m
i
ν
i
ν
i
.
(
3.22
)
The kinetic term o
f
Majorana neutrinos turns out to be
L
k
in
et
i
c
=i
ν
L
γ
μ
∂
μ
ν
L
=
i
ν
L
γ
μ
∂
μ
ν
L
=
i
2
ν
γ
μ
∂
μ
ν
=
i
2
3
k
=1
ν
k
γ
μ
∂
μ
ν
k
,
(
3.23
)
w
h
ere we
h
ave use
d
a
g
eneric re
l
ations
h
ip
(
ψ
L
)
c
γ
μ
∂
μ
(
ψ
L
)
c
=
ψ
L
γ
μ
∂
μ
ψ
L
.
T
h
i
s
relationship can easily be proved by takin
g
account o
f
∂
μ
(
ψ
L
)
c
γ
μ
(
ψ
L
)
c
=
0;
i
.e., we
h
ave
(
ψ
L
)
c
γ
μ
∂
μ
(
ψ
L
)
c
=
−
∂
μ
(
ψ
L
)
c
γ
μ
(
ψ
L
)
c
=
−
∂
μ
(
ψ
L
)
c
γ
μ
(
ψ
L
)
c
T
=
C
ψ
L
T
T
γ
T
μ
∂
μ
(
ψ
L
)
T
C
T
=
ψ
L
γ
μ
∂
μ
ψ
L
,
(
3.24
)
w
h
e
r
e
C
T
γ
T
μ
C
T
=
γ
μ
,
which can be read off from Eq.
(
3.8
)
, has been used
.
I
t is worth pointing out that the factor 1
/
2in
L
Majoran
a
allows us to
g
et the Dirac equation o
f
massive Majorana neutrinos analo
g
ous to that o
f
m
assive Dirac neutrinos. To see this point more clearl
y
, let us consider th
e
L
agrangian of free Majorana neutrinos
(
i.e., their kinetic and mass terms
):
L
ν
=
i
ν
L
γ
μ
∂
μ
ν
L
−
1
2
ν
L
M
L
MM
(
ν
L
)
c
+h
.
c
.
=iν
L
γ
μ
∂
μ
ν
L
−
1
2
ν
L
$
M
ν
MM
(
ν
L
)
c
+h
.
c
.
=
1
2
i
ν
γ
μ
∂
μ
ν
−
ν
$
M
ν
M
M
ν
=
−
1
2
i
∂
μ
ν
γ
μ
ν
+
ν
$
M
ν
M
M
ν
,
(
3.25
)
whe
r
e
∂
μ
(
ν
γ
μ
ν
)
= 0 has been used. Then we substitute
L
ν
i
n
to the
E
ule
r
-
L
a
g
ran
g
e equation
∂
μ
∂
L
ν
∂
∂
μ
ν
−
∂
L
ν
∂
ν
=0
(
3.26
)
a
n
d
o
b
tain t
h
e Dirac equation
i
γ
μ
∂
μ
ν
−
$
M
ν
MM
ν
=0
.
(
3.27
)
More explicitl
y
,
i
γ
μ
∂
μ
ν
k
−
m
k
ν
k
=
0holds
(
for
k
=1
,
2
,
3
)
.Thatiswhyth
e
facto
r
1
/
2
in
L
M
ajorana
makes se
n
se.
T
he weak charged-current interactions of three neutrinos in Eq.
(
3.9
)
c
an now be rewritten in terms of their mass eigenstates
ν
L
=
V
†
ν
L
.
In th
e
c
hosen basis where the flavor and mass eigenstates of three charged lepton
s
a
re identical, the expression o
f
L
cc
f
or Ma
j
orana neutrinos is the same as
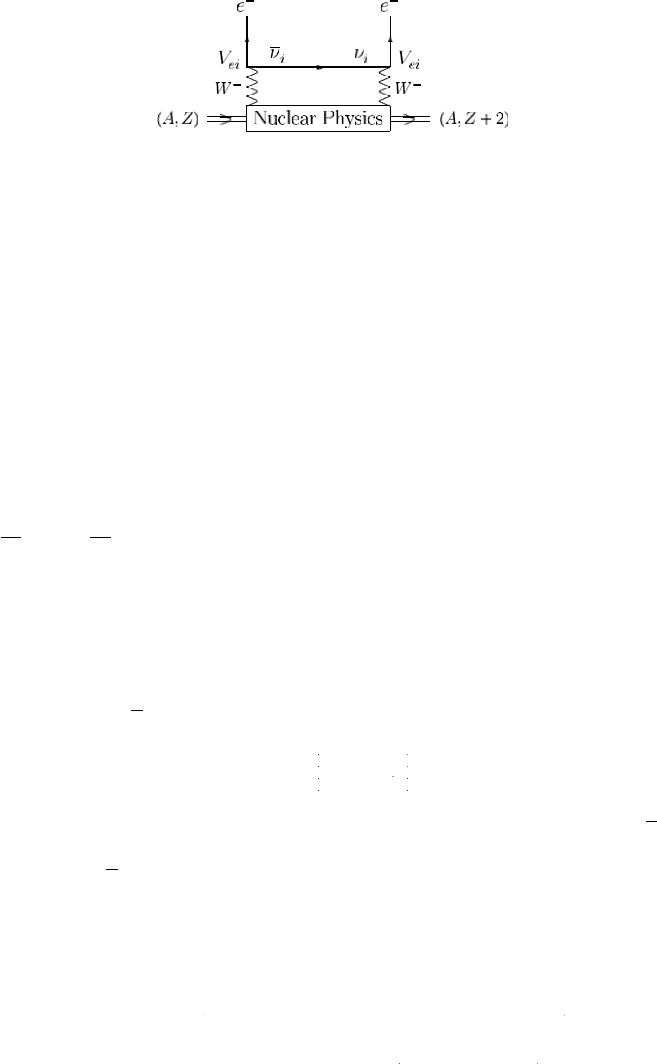
3.2 Dirac an
d
Majorana Neutrino Mass Terms 75
Fi
g
.3.6 T
h
e0
ν
2
β
d
ecay o
f
some even-even nuclei via the exchan
g
eo
f
virtua
l
Majorana neutrinos between two beta decays
that given in Eq.
(
3.16
)
for Dirac neutrinos. The unitary matrix
V
i
s just t
he
3
×
3
Majorana neutrino mixin
g
matrix, which contains two more irremovabl
e
CP-violating phases than the 3
×
3
Dirac neutrino mixing matrix
(
see Sectio
n
3
.5 for detailed discussions
)
.
T
he most salient feature of massive Ma
j
orana neutrinos is lepton numbe
r
violation. Let us make the global phase transformations
l
(
x
)
→
e
i
Φ
l
(
x
)
,
ν
L
(
x
)
→
e
i
Φ
ν
L
(
x
)
,
(
3.28
)
w
h
ere
l
s
tands for the column vector of
e
,
μ
an
d
τ
fields
,
and
Φ
i
sanar
b
itrar
y
s
pacetime-independent phase.
O
ne can immediatel
y
see that the kinetic ter
m
L
k
ineti
c
and the char
g
ed-current interaction ter
m
L
cc
a
re invariant under these
transformations, but the mass term
L
M
ajorana
i
s
n
ot
in
va
ri
a
n
t because o
f
bot
h
ν
L
→
e
−
i
Φ
ν
L
a
nd
(
ν
L
)
c
→
e
−
i
Φ
(
ν
L
)
c
.
Theleptonnumberisthere
f
ore violate
d
f
or massive Ma
j
orana neutrinos. Similar to the case of Dirac neutrinos, the
l
epton
fl
avor violation o
f
Majorana neutrinos is described b
y
V
.
T
he 0
ν
2
β
d
ecay
(
A
,Z
)
→
(
A
,Z
+
2
)
+
2
e
−
is a clean si
g
nature o
f
the Ma
-
j
orana nature of massive neutrinos. Fig. 3.6 shows that this lepton-number-
vio
l
atin
g
process can occur w
h
en t
h
ere exists neutrino-antineutrino mixin
g
i
nduced by the Majorana mass term
(
i.e., the neutrino mass eigenstates ar
e
s
elf-conjugate,
ν
i
=
ν
i
)
. The effective mass of the
0
ν2
β
d
ecay is defined a
s
m
e
e
≡
i
m
i
V
2
ei
VV
,
(
3.29
)
w
h
ere m
i
comes from the helicity suppression facto
r
m
i
/E
for th
e
ν
i
=
ν
i
exc
h
an
g
e
b
etween two or
d
inary
b
eta
d
ecays wit
h
E
bein
g
the ener
g
yo
f
the
virtua
l
ν
i
or
ν
i
. Current experimental data onl
yy
ield an upper boun
d
m
ee
<
0
.
2
3eV
(
or
<
0
.
8
5 eV as a more conservative bound
)
at the
2
σ
l
evel
(
Fogl
i
et al
.
,
2008a
).
3.2.3 Hybrid Mass Terms and
S
eesaw Mechanism
s
Similar to Eq.
(
3.18
),
N
R
NN
and its charge-conjugate counterpart
(
N
R
NN
)
c
ca
n
also
f
orm a Majorana mass term. Hence it is possible to write out the
f
ollowin
g
h
ybrid neutrino mass terms in terms o
f
ν
L
,
N
R
N
N
,(
ν
L
)
c
and
(
N
R
N
N
)
c
fields
:
