Xing Zh., Zhou Sh. Neutrinos in Particle Physics, Astronomy and Cosmology
Подождите немного. Документ загружается.

86 3 Neutrinos beyond the
S
tandard Mode
l
a
treatment will trans
f
er
C
P violation
f
rom the Yukawa interactions to the
weak char
g
ed-current interactions. Then lepton flavor mixin
g
and CP viola-
tion are
d
escri
b
e
db
yt
h
e
3
×
3
unitary matrix
V
g
iven in Eq.
(
3.16
)
, analogous
to t
h
e
3
×
3
unitary matrix o
f
quark
fl
avor mixin
g
and
C
P violation
g
ive
n
i
nEq.
(
2.50
)
. In other words, the source of CP violation is the irremovable
c
omplex phase
(
s
)
in the flavor mixing matrix of quarks or leptons. That i
s
wh
y
we claim that
C
P violation stems
f
rom the coexistence o
f
L
F
a
n
d
L
Y
within the SM and, in most cases, be
y
ond the SM
.
I
t is worth reiterating that the process of spontaneous gauge symmetr
y
breakin
g
in the SM does not spontaneously violate CP.
A
fter the Hi
gg
s dou-
ble
t
H
acquires its vacuum expectation value
(
i.e.
,
φ
+
→
0
an
d
φ
0
→
v
/
√
2
w
i
th
v
being real
)
, as described in Section 2.1.4, we obtain three massive
g
au
g
e boson
s
W
±
μ
W
a
n
d
Z
μ
Z
a
s well as one massless
g
au
g
e boso
n
A
μ
.
A
ccordin
g
to t
h
eir re
l
ations wit
h
W
i
μ
W
an
d
B
μ
s
hown in Eqs.
(
2.42
)
and
(
2.43
)
, it is easy
to
fi
nd out the trans
f
ormation properties o
f
these ph
y
sical
fi
elds under
C
P:
W
±
μ
W
CP
−
→
−
W
∓
μ
,Z
μ
Z
C
P
−→ −
Z
μ
,A
μ
C
P
−→ −
A
μ
,
(
3.63
)
w
i
th
x
→−
x
u
nder P and
C
P
f
or each
fi
eld. In contrast, the neutral
H
i
gg
s boso
n
h
i
s a CP-even particle.
A
fter spontaneous electroweak s
y
m
-
m
etry breaking, we are left with the quark mass matrice
s
M
u
MM
=
vY
u
YY
/
√
2
a
n
d
M
d
M
=
vY
d
YY
/
√
2
or t
h
e
l
epton mass matrices
M
D
M
M
=
vY
ν
YY
/
√
2
a
n
d
M
l
M
=
vY
l
YY
/
√
2.
The conditions of CP invariance given in Eq.
(
3.60
)
,
(
3.61
)
or
(
3.62
)
can
therefore be replaced with the corresponding mass matrices.
3
.4 Electroma
g
netic Properties o
f
Massive Neutrino
s
The e
ff
ective electroma
g
netic vertex o
f
a
f
ermion interactin
g
with the photo
n
i
s illustrated in Fi
g
.3.7.
A
lthou
g
h a neutrino does not possess any electri
c
c
harge, it can have electromagnetic interactions via quantum loops. One ma
y
s
ummarize such interactions by means o
f
the
f
ollowin
g
e
ff
ective interactio
n
term
(
Mohapatra and Pal, 2004
)
:
L
EM
=
ψΓ
μ
Γ
ψA
μ
≡
J
μ
J
(
x
)
A
μ
(
x
)
,
(
3.64
)
where the
f
orm o
f
the electroma
g
netic curren
t
J
μ
J
(
x
)
is our present concern.
D
irac and Majorana neutrinos couple to the photon in different ways, which
a
re described by their respective electroma
g
netic
f
orm
f
actors.
3.4.1 Electromagnet
i
c Form Factor
s
F
or an arbitrary Dirac particle
(
e.g., a Dirac neutrino
)
, let us write down the
mat
rix
e
l
e
m
e
n
tof
J
μ
J
(
x
)
between two one-particle states
:
ψ
(
p
)
|
J
μ
J
(
x
)
|
ψ
(
p
)
=e
−
i
qx
ψ
(
p
)
|
J
μ
J
(
0
)
|
ψ
(
p
)
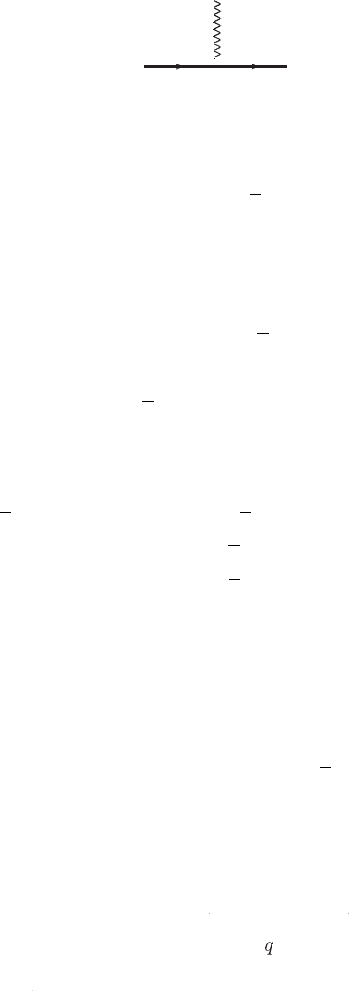
3.4 Electromagnetic Properties o
f
Massive Neutrinos 87
ψ
(
p
)
ψ
(
p
)
•
A
μ
(
q
)
>
•
>>
•
>
>>
>
>
>
>>
>
>
>
>>
>
>
>
>>
>
>
>
>>
>
>
>
>>
>
>
>
>>
>
>
>
••
>>
••••
>>>>
•••••••
>
>>
>>>>
>>
>>>>>>>
>>>>>>>
>
>>
>>>>
>>
>>>>>>>
>>>>>>>
>
>>
>>>>
>>
>>>>>>>
>>>>>>>
>
>>
>>>>
>>
>>>>>>>
>>>>>>>
>
>>
>>>>
>>
>>>>>>>
>>>>>>>
>
>>
>>>>
>>
>>>>>>>
>>>>>>>
>
>>
>>>>
>
>
>
>
>
>>>>
>
>
>
>>>>
Fig. 3.7 The effective electromagnetic vertex of a fermion, wher
e
A
μ
i
sthe
p
hoton
fi
e
l
dw
i
th
q
=
p
−
p
=e
−
i
qx
u
(
p
)
Γ
μ
Γ
(
p
,
p
)
u
(
p
)
(
3.65
)
w
i
th
q
=
p
−
p
. Because
J
μ
J
(
x
)
is a Lorentz vector, the electromagnetic verte
x
fu
n
ct
i
o
n
Γ
μ
Γ
(
p
,
p
)
must be a Lorentz vector too. The electromagnetic curren
t
c
onservation
(
o
r
U
(
1
)
Q
g
auge symmetry
)
requires
∂
μ
J
μ
J
(
x
)
= 0, leading t
o
ψ
(
p
)
|
∂
μ
J
μ
J
(
x
)
|
ψ
(
p
)
=(
−
i
q
μ
)e
−
i
q
x
u
(
p
)
Γ
μ
Γ
(
p
,
p
)
u
(
p
)
=
0
.
(
3.66
)
Th
us
q
μ
u
(
p
)
Γ
μ
Γ
(
p, p
)
u
(
p
)
=0
(
3.67
)
h
olds as one o
f
the model-independent constraints on the
f
orm o
f
Γ
μ
Γ
(
p
,
p
)
.
In addition, the Hermiticit
y
of
J
μ
J
(
x
)
or its matrix element implie
s
e
−
i
q
x
u
(
p
)
Γ
μ
Γ
(
p
,
p
)
u
(
p
)
=
e
+i
qx
u
(
p
)
Γ
μ
Γ
(
p
,
p
)
u
(
p
)
†
=
e
+
i
qx
u
(
p
)
γ
0
Γ
†
μ
Γ
(
p
,
p
)
γ
0
u
(
p
)
=
e
−
i
qx
u
(
p
)
γ
0
Γ
†
μ
Γ
(
p
,p
)
γ
0
u
(
p
)
,
(
3.68
)
f
rom which we immediately arrive at the second constraint o
n
Γ
μ
Γ
(
p, p
):
Γ
μ
Γ
(
p
,
p
)
=
γ
0
Γ
†
μ
Γ
(
p
,p
)
γ
0
.
(
3.69
)
Because of p
2
=
p
2
=
m
2
wit
h
m
b
eing the fermion mass, we have
(
p
+
p
)
2
=
4
m
2
−
q
2
.H
e
n
ce
Γ
μ
Γ
(
p
,
p
)
depends only on the Lorentz-invariant quantit
y
q
2
.
A
careful anal
y
sis of the Lorentz structure of
u
(
p
)
Γ
μ
Γ
(
p
,
p
)
u
(
p
)
,withthe
h
elp of the Gordon-like identities and the constraints given in Eqs.
(
3.67
)
and
(
3.69
)
,showstha
t
Γ
μ
Γ
(
p
,
p
)
may in general consist of four independent term
s
(
Kayser, 1982; 1984; Nieves, 1982; Mohapatra and Pal, 2004; Nowakowsk
i
et
al.
,
2005; Giunti and Studenikin, 2009
):
Γ
μ
Γ
(
p
,
p
)
=
f
Q
ff
(
q
2
)
γ
μ
+
f
M
ff
(
q
2
)
i
σ
μν
q
ν
+
f
E
ff
(
q
2
)
σ
μν
q
ν
γ
5
+
f
A
f
(
q
2
)
q
2
γ
μ
−
q
μ
/
q
/
/
γ
5
,
(
3.70
)
whe
r
e
f
Q
f
f
(
q
2
),
f
M
f
f
(
q
2
),
f
E
f
f
(
q
2
)
an
d
f
A
f
(
q
2
)
are usually referred to as the charge
,
m
a
g
netic dipole, electric dipole and anapole form factors, respectively. In th
e
n
on-relativistic limit of
L
EM
,
it is easy to find that
f
Q
ff
(
0
)
=
Q
r
epresen
ts

88 3 Neutrinos beyond the
S
tandard Mode
l
the electric char
g
eo
f
the particle
,
f
M
ff
(
0
)
≡
μ
d
enotes t
h
ema
g
netic
d
ipo
le
m
oment of the particle
(
i.e.
,
L
EM
(
f
M
f
f
)=
−
μ
σ
·
B
wit
h
B
bein
g
the static
m
agnetic field
),
f
E
ff
(
0
)
≡
s
tands for the electric dipole moment of the particle
(
i.e.
,
L
E
M
(
f
E
ff
)
=
−
σ
·
E
w
i
th
E
b
eing the static electric field
)
,and
f
A
f
(
0
)
c
orresponds to the Zeldovich anapole moment of the particle
(
i.e.,
L
EM
(
f
A
f
)
∝
f
A
f
(
0
)
σ
·
[
∇
× B
−
˙
E
]) (
see, e.g., Nowakowsk
i
et al.
, 2005
)
. One can observe
that these form factors are not only Lorentz-invariant but also real
(
i.e.,
Im
f
Q
ff
=
I
m
f
M
f
f
=Im
f
E
ff
=I
m
f
A
f
=0
)
. The latter is actually guaranteed b
y
the Hermiticity condition in Eq.
(
3.69
)
.
G
iven the
f
orm o
f
Γ
μ
Γ
i
nEq.
(
3.70
)
, it is straightforward to check the C
P
p
ro
p
erties o
f
L
EM
i
nEq.
(
3.64
)
. Note that the photon field transforms as
A
μ
→−
A
μ
under
C
P, an
d
5
ψγ
μ
ψ
C
P
−
→
−
ψ
γ
μ
ψ,
ψγ
μ
γ
5
ψ
C
P
−→ −
ψγ
μ
γ
5
ψ,
ψ
σ
μ
ν
ψ
CP
−
→
−
ψσ
μν
ψ,
ψ
σ
μν
γ
5
ψ
C
P
−→
+
ψ
σ
μν
γ
5
ψ.
(
3.71
)
Therefore, only the term proportional to
f
E
f
f
in
L
EM
i
s CP-violating. If CP
were conserved, then this term would vanish
(
i.e.,
f
E
ff
=
0 would hold
)
.Al-
thou
g
h there is no experimental hint at CP violation in the lepton sector, we
expect that it should exist as in the quark sector. In any case, all four for
m
facto
r
sa
r
efi
ni
te fo
r
a
Dir
ac
n
eut
rin
o.
I
f neutrinos are massive Majorana particles, their electromagnetic proper
-
ties will be rather different. The reason is simply that Majorana particles ar
e
t
h
eir own antipartic
l
es an
d
t
h
us can
b
e
d
escri
b
e
db
yusin
g
asma
ll
er num
b
er
of degrees of freedom.
A
free Majorana neutrino field
ψ
i
sb
y
definition equal
to its char
g
e-conju
g
ate field
ψ
c
=
C
ψ
T
u
ptoa
g
lobal phase. Then
ψΓ
μ
Γ
ψ
=
ψ
c
Γ
μ
Γ
ψ
c
=
ψ
T
C
Γ
μ
Γ
C
ψ
T
=
ψ
T
C
Γ
μ
Γ
C
ψ
T
T
=
−
ψ
C
T
Γ
T
μ
Γ
C
T
ψ,
(
3.72
)
f
r
o
m
w
hi
c
h
o
n
ea
rri
ves at
Γ
μ
Γ
=
−
C
T
Γ
T
μ
Γ
C
T
=
C
Γ
T
μ
Γ
C
−
1
.
(
3.73
)
Substituting Eq.
(
3.70
)
into the right-hand side of Eq.
(
3.73
)
and taking
accou
n
tof
C
γ
T
μ
C
−
1
=
−
γ
μ
,
C
(
γ
μ
γ
5
)
T
C
−
1
=+
γ
μ
γ
5
,
C
σ
T
μν
C
−
1
=
−
σ
μ
ν
a
n
d
C
(
σ
μ
ν
γ
5
)
T
C
−
1
=
−
σ
μν
γ
5
,
we obtai
n
Γ
μ
Γ
(
p
,
p
)
=
−
f
Q
ff
(
q
2
)
γ
μ
−
f
M
ff
(
q
2
)
i
σ
μν
q
ν
−
f
E
ff
(
q
2
)
σ
μν
q
ν
γ
5
+
f
A
f
(
q
2
)
q
2
γ
μ
−
q
μ
/
q
/
/
γ
5
.
(
3.74
)
A
comparison between Eqs.
(
3.70
)
and
(
3.74
)
leads t
o
5
T
akin
g
account o
f
C
−
1
σ
μ
ν
C
=
−
σ
T
μ
ν
a
n
d
C
−
1
γ
5
C
=
γ
T
5
,onema
y
easi
ly
prov
e
tha
t
ψ
σ
μν
γ
5
ψ
i
s odd under both C and P. Thu
s
ψ
σ
μ
ν
γ
5
ψ is CP-even
.
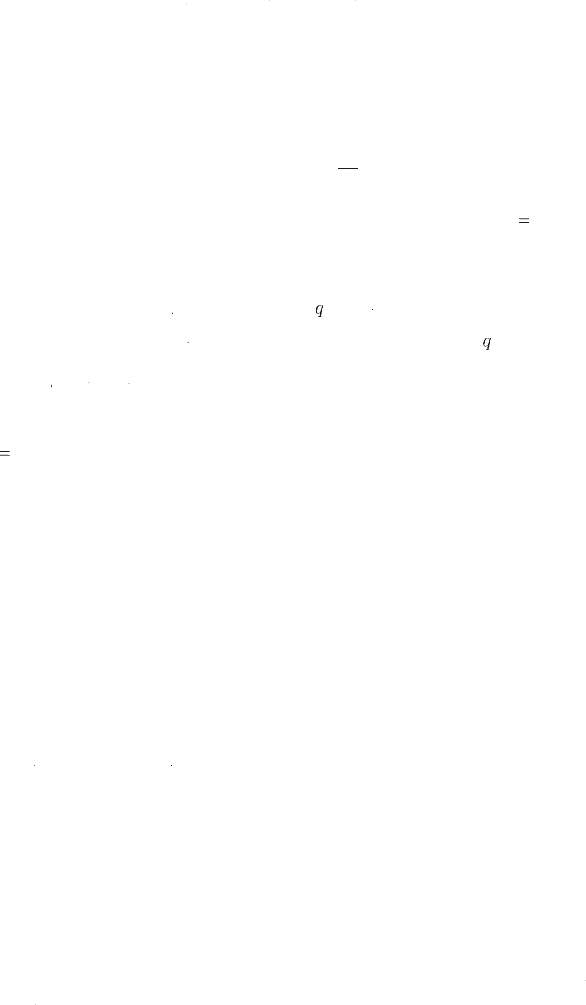
3.4 Electromagnetic Properties o
f
Massive Neutrinos 89
f
Q
ff
(
q
2
)
=
f
M
ff
(
q
2
)=
f
E
f
f
(
q
2
)
=0
.
(
3.75
)
This result means that a Ma
j
orana neutrino onl
y
has the anapole
f
orm
f
actor
f
A
f
(
q
2
)(
Schechter and Valle, 1981; Nieves, 1982
)
.
M
ore generally, one may write out the matrix elements of the electro
-
m
a
g
net
i
c current
J
μ
J
(
x
)
between two different states
(
i.e., the incoming and
outgoing particles are different
)
:
ψ
j
(
p
)
|
J
μ
J
(
x
)
|
ψ
i
(
p
)
=e
−
i
qx
u
j
(
p
)
Γ
ij
μ
Γ
(
p
,
p
)
u
i
(
p
)
,
(
3.76
)
whe
r
e
q
=
p
−
p
toget
h
er wit
h
p
2
=
m
2
i
a
n
d
p
2
=
m
2
j
(
for
i
=
j
)
.Herethe
e
l
ectroma
g
netic vertex matrix
Γ
μ
Γ
(
p
,
p
)
can be decomposed into the following
L
orentz-invariant form in terms of four form factors
:
Γ
μ
Γ
(
p
,
p
)=
F
Q
FF
(
q
2
)
q
2
γ
μ
−
q
μ
/
q
//
+
F
M
FF
(
q
2
)i
σ
μν
q
ν
+
F
E
FF
(
q
2
)
σ
μν
q
ν
γ
5
+
F
A
F
(
q
2
)
q
2
γ
μ
−
q
μ
/
q
//
γ
5
,
(
3.77
)
whe
r
e
F
Q
F
F
,
F
M
F
F
,
F
E
F
F
a
n
d
F
A
F
a
r
eallthe2
×
2
matrices in the space o
f
neutrino
m
ass eigenstates
(
Shrock, 1982
)
. The diagonal case
(
i.e.
,
i
=
j
)
has been
d
iscussed above, from Eq.
(
3.65
)
to Eq.
(
3.75
)
. In the off-diagonal case
(
i.e.,
i
=
j
)
, the Hermiticity of
J
μ
J
(
x
)
is no more a constraint o
n
Γ
μ
Γ
(
p
,
p
)
for
D
irac neutrinos because Eq.
(
3.68
)
only holds fo
r
i
=
j
.
It is now
p
ossible fo
r
Majorana neutrinos to have finite
transition
d
ipo
l
e moments, simp
l
y
b
ecaus
e
E
qs.
(
3.72
)
—
(
3.75
)
do not hold whe
n
ψ
i
a
n
d
ψ
j
r
epresent di
ff
erent
fl
avors.
W
e conclude that Dirac neutrinos may have both electric and magneti
c
d
ipo
l
emoments,w
h
i
l
e Majorana neutrinos
h
ave neit
h
er e
l
ectric nor magneti
c
d
ipo
l
e moments. But massive Ma
j
orana neutrinos can
h
av
e
transition
d
ipo
l
e
m
oments which involve two different neutrino flavors in the initial and fina
l
s
tates, so can massive
D
irac neutrinos.
3.4.2 Magnetic and Electric Dipole Moment
s
The ma
g
netic and electric dipole moments o
f
massive neutrinos, denoted a
s
μ
≡
F
M
FF
(
0
)
and
≡
F
E
FF
(
0
)
, are interesting in both theories and experiment
s
because they are closely related to the dynamics of neutrino mass generatio
n
a
nd to the characteristic o
f
new ph
y
sics.
Let us consider a minimal extension of the SM in which three right-
h
an
d
e
d
neutrinos are intro
d
uce
d
an
dl
epton num
b
er conservation is require
d
,
j
ust as described in
S
ection 3.2.1. In this case massive neutrinos are Dira
c
particles and their magnetic and electric dipole moments can be evaluate
d
by calculating the Feynman diagrams in Fig. 3.8
(
Marciano and Sanda, 1977
;
L
ee and
S
hrock, 1977; Fu
j
ikawa and
S
hrock, 1980;
S
hrock, 1982; Pal and
Wolfenstein, 1982
)
. Taking account of the smallness of both m
2
α
/M
2
W
M
M
a
nd
m
2
i
/M
2
W
MM
,
w
h
ere
m
α
(
for
α
=
e
,
μ
,τ
)
an
d
m
i
(
for
i
=
1
,
2
,
3
)
stand respectively
f
or the charged-lepton and neutrino masses, one obtains
(
Cabral-Rosetti
et
a
l
.
,
2000; Dvornikov and Studenikin, 2004; Giunti and Studenikin, 2009
)

90 3 Neutrinos beyond the
S
tandard Mode
l
Fig. 3.8
O
ne-loop Feynman diagrams contributing to the magnetic and electric
di
p
ole moments o
f
massive Dirac neutrinos, wher
e
α
=
e
,
μ
,τ
a
n
d
i
,
j
=
1
,
2
,
3
μ
D
i
j
=
3
e
G
F
m
i
3
2
√
2
π
2
1
+
m
j
m
i
α
2
−
m
2
α
M
2
W
MM
V
αi
VV
V
∗
αj
VV
,
D
ij
=
3
e
G
F
m
i
32
√
2
π
2
1
−
m
j
m
i
α
2
−
m
2
α
M
2
W
MM
V
αi
VV
V
∗
αj
VV
,
(
3.78
)
to an excellent degree of accuracy. Her
e
V
αi
VV
a
nd
V
αj
VV
are the elements of the
u
nitary lepton
fl
avor mixin
g
matrix
V
.S
ome discussions are in order.
(
1
)
In the diagonal case
(
i.e.
,
i
=
j
)
, we are left with vanishing electri
c
d
ipole moments
(
i.e.
,
D
ii
=0
)
. The magnetic dipole moment
s
μ
D
i
i
are finit
e
a
n
d
proportiona
l
to t
h
e neutrino masses
m
i
(
fo
r
i
=
1
,
2
,
3):
μ
D
ii
=
3
e
G
F
m
i
8
√
2
π
2
1
−
1
2
α
m
2
α
M
2
W
M
M
|
V
αi
VV
|
2
.
(
3.79
)
H
ence a massless Dirac neutrino in the
S
Mhasnoma
g
netic dipole moment
.
In the leadin
g
-order approximation
,
μ
D
ii
are independent of the stren
g
th of
l
epton flavor mixing and have tiny values
μ
D
ii
≈
3
e
G
F
m
i
8
√
2
π
2
≈
3
×
10
−
1
9
m
i
1
eV
μ
B
,
(
3.80
)
w
h
e
r
e
μ
B
=
e
/
(2
m
e
)
is the Bohr magneton. Give
n
m
i
1
eV, the ma
g
nitud
e
of
μ
D
i
i
i
s far below its present experimental upper bound
(
<
afe
w
×
1
0
−
1
1
μ
B
)
.
(
2
)
In the off-diagonal case
(
i.e.,
i
=
j
)
, the unitarity o
f
V
allows us to
s
implify Eq.
(
3.78
)
t
o
μ
D
ij
=
−
3
e
G
F
m
i
32
√
2
π
2
1
+
m
j
m
i
α
m
2
α
M
2
W
MM
V
αi
VV
V
∗
αj
VV
,
D
ij
=
−
3e
G
F
m
i
3
2
√
2
π
2
1
−
m
j
m
i
α
m
2
α
M
2
W
MM
V
αi
VV
V
∗
αj
VV
.
(
3.81
)
We see that the magnitudes o
f
μ
D
i
j
an
d
D
i
j
(
for
i
=
j
)
, compared with that o
f
μ
D
ii
, are further su
pp
ressed due to the smallness of m
2
α
/M
2
W
M
M
. Similar to th
e
expression given in Eq.
(
3.80
),

3.4 Electromagnetic Properties o
f
Massive Neutrinos 9
1
μ
D
i
j
≈−
4
×
1
0
−
23
m
i
+
m
j
1e
V
α
m
2
α
m
2
τ
V
αi
VV
V
∗
αj
VV
μ
B
,
D
ij
≈−
4
×
10
−
23
m
i
−
m
j
1eV
α
m
2
α
m
2
τ
V
αi
VV
V
∗
αj
VV
μ
B
,
(
3.82
)
wh
i
ch ca
ni
llust
r
ate how s
m
all
μ
D
ij
a
n
d
D
i
j
a
re
(
see, e.g., Raffelt, 1996, 1999
;
Giunti and Studenikin, 2009
).
(
3
)
Although Majorana neutrinos do not have intrinsic
(
i
=
j
)
magnetic
a
nd electric dipole moments, they may have finite transition
(
i
=
j
)
dipole
m
oments as we have
p
ointed out in
S
ection 3.4.1. Because o
f
the
f
act tha
t
Majorana neutrinos are their own antiparticles, their magnetic and electric
d
ipole moments can also
g
et contributions
f
rom two additional one-loop Feyn-
m
an dia
g
rams involvin
g
the char
g
e-conju
g
ate
fi
elds o
f
ν
i
,
ν
j
ν
,
l
α
,
W
±
a
n
d
γ
sh
own in Fig. 3.
8
6
.
In this case one obtains
(
Shrock, 1982
)
μ
M
ij
=
−
3
eG
F
i
16
√
2
π
2
m
i
+
m
j
α
m
2
α
M
2
W
MM
Im
V
αi
VV
V
∗
αj
VV
,
M
ij
=
−
3
e
G
F
1
6
√
2
π
2
m
i
−
m
j
α
m
2
α
M
2
W
M
M
Re
V
αi
VV
V
∗
αj
VV
,
(
3.83
)
w
h
ere
m
i
=
m
j
must hold. Comparing between Eqs.
(
3.81
)
and
(
3.83
)
,we
observe that the ma
g
nitudes o
f
μ
M
ij
a
nd
M
ij
are the same order as those of
μ
D
ij
a
n
d
D
ij
in most cases, althou
g
hthe
C
P-violatin
g
phases hidden in
V
αi
VV
V
∗
αj
VV
a
r
e
possible to give rise to significant cancellations in some cases
.
(
4
)
The fact tha
t
μ
ij
a
n
d
i
j
a
re proportiona
l
to
m
i
or
m
j
ca
n
be u
n-
d
erstood in the
f
ollowin
g
way. Note that both tensor- and pseudotensor-like
s
pinor bilinears are chirality-changing operators, which link the left-handed
s
tate to the right-handed one
(
Mohapatra and Pal, 2004
)
7
:
ψ
σ
μ
ν
ψ
=
ψ
L
σ
μ
ν
ψ
R
+h
.
c
.,
ψ
σ
μν
γ
5
ψ
=
ψ
L
σ
μ
ν
γ
5
ψ
R
−
h
.
c
.
.
(
3.84
)
Note also that the sa
m
e
r
elat
i
o
n
s hold when
ψ
i
srep
l
ace
db
yitsc
h
ar
g
e
-
c
onju
g
ate fiel
d
ψ
c
f
or Majorana neutrinos. Because
(
ν
i
)
R
and
(
ν
j
ν
)
R
do no
t
h
ave any interactions wit
h
W
±
in Fig. 3.8, it seems that only
(
ν
i
)
L
and
(
ν
j
ν
)
L
a
re
fl
owin
g
alon
g
the external
f
ermion lines. To obtain a chirality-chan
g
in
g
c
ontribution from the effective
(
one-loop
)
electromagnetic vertex, one has t
o
put a mass insertion on one of the external legs in the Feynman diagrams
.
A
s a result, the ma
g
netic and electric dipole moments must involve
m
i
a
n
d
m
j
,
the masses o
f
ν
i
a
nd
ν
j
ν
neutr
i
nos
.
6
H
ere we confine ourselves to a simple extension of the SM with three known
neutrinos to be massive Majorana particles, as discussed in Section 3.2.2
.
7
T
hat is why both ma
g
netic and electric dipole moments must vanish
f
or a Weyl
neutrino, because it is massless and does not possess the right-handed component.
92 3 Neutrinos beyond the
S
tandard Mode
l
(
5
)
Is the magnetic or electric dipole moment of a neutrino always pro
-
portional to its mass? The answer may be ne
g
ative if new physics beyon
d
t
h
e
SU
(
2
)
L
×
U
(
1
)
Y
g
auge theory is involved
(
Giunti and Studenikin, 2009
).
F
or instance, a new term proportiona
l
to t
h
ec
h
ar
g
e
d
-
l
epton mass can con
-
tribute to the ma
g
netic dipole moment of a massive Dirac neutrino in th
e
SU
(
2
)
L
×
SU
(
2
)
R
×
U
(
1
)
Y
m
odel with broken left-right symmetry
(
Kim, 1976
;
Marciano and
S
anda, 1977;
C
zakon
et al
., 1999
)
. Depending on the details of
this model, such a term might cancel or exceed the term proportional to th
e
n
eutrino mass in the expression of the magnetic dipole moment
.
Finite ma
g
netic and electric dipole moments o
f
massive neutrinos ma
y
produce a variety of new processes beyond the SM
(
Strumia and Vissani,
2
006; Giunti and Studenikin, 2009
)
. For example,
(
a
)
radiative neutrino de
-
c
a
ys
ν
i
→
ν
j
ν
+
γ
can ha
pp
en, so can the
C
herenkov radiation o
f
neutri-
n
os in an external electromagnetic field;
(
b
)
the elastic neutrino-electron or
n
eutrino-nuc
l
eon scatterin
g
can
b
eme
d
iate
db
yt
h
ema
g
netic an
d
e
l
ectri
c
d
ipole moments;
(
c
)
the phenomenon of precession of the neutrino spin ca
n
occur in an external magnetic field;
(
d
)
the photon
(
or plasmon
)
can de-
c
ay into a neutrino-antineutrino pair in a plasma
(
i.e.
,
γ
∗
→
ν
ν
)
. Of course
,
n
on-vanishin
g
electroma
g
netic dipole moments contribute to neutrino masses
too. The following two subsections will briefly cover the topics of radiative
n
eutrino decays and electroma
g
netic neutrino-electron scatterin
g
e
ff
ects.
3.4.3 Radiative Deca
y
so
f
Massive Neutrino
s
If the electromagnetic moments of a massive neutrino
ν
i
are finite, it ca
n
d
ecay into a
l
i
gh
ter neutrino
ν
j
ν
an
d
ap
h
oto
n
γ
v
ia Fi
g
.3.7,w
h
ere t
he
i
ncoming and outgoing fermions are replaced respectively by
ν
i
a
nd
ν
j
ν
.Th
e
Lo
r
e
n
t
z-in
va
ri
a
n
tve
r
te
xm
at
rix
o
f
t
hi
s
ν
i
→
ν
j
ν
+
γ
p
rocess is in genera
l
d
escribed b
y
Γ
μ
Γ
(
p
,
p
)
in Eq.
(
3.77
)
. Becaus
e
q
2
=
0and
q
μ
ε
μ
=
0 hold for
a
rea
l
p
h
oto
n
γ
(
Mohapatra and Pal, 2004
)
,where
ε
μ
represents t
h
ep
h
oto
n
polarization vector, the
f
orm o
f
Γ
μ
Γ
(
p
,
p
)
can be simplified to
Γ
μ
Γ
(
p
,
p
)
=
[
i
F
M
FF
(
0
)
+
F
E
FF
(
0
)
γ
5
]
σ
μν
q
ν
.
(
3.85
)
B
y
de
fi
nition,
F
ij
M
FF
(
0
)
≡
μ
ij
a
n
d
F
ij
E
F
F
(
0
)
≡
ij
a
re just t
h
ema
g
netic an
d
e
l
ectric
transition di
p
ole moments between
ν
i
an
d
ν
j
ν
n
eutrinos. Given the transition
m
atrix elemen
t
u
j
(
p
)
Γ
i
j
μ
Γ
(
p
,
p
)
u
i
(
p
)
, it is straightforward to calculate th
e
d
ecay rate. In the rest frame of the decaying neutrino ν
i
,
one o
b
tain
s
Γ
ν
ΓΓ
i
→
ν
j
+
γ
=
m
2
i
−
m
2
j
3
8
π
m
3
i
μ
ij
2
+
ij
2
.
(
3.86
)
This result is valid
f
or both Dirac and Majorana neutrinos
.
I
n
t
h
ef
r
a
m
ewo
rk
of t
h
e
SU
(
2
)
L
×
U
(
1
)
Y
g
au
g
e theory with three massiv
e
D
irac
(
or Majorana
)
neutrinos, the radiative deca
y
ν
i
→
ν
j
ν
+
γ
i
smediate
d

3.4 Electromagnetic Properties o
f
Massive Neutrinos 93
by the one-loop Feynman diagrams
(
and their charge-conjugate diagrams
)
s
hown in Fi
g
. 3.8. The explicit expressions of
μ
ij
and
ij
h
ave been
g
iven in
E
q.
(
3.81
)
for Dirac neutrinos and in Eq.
(
3.83
)
for Majorana neutrinos. As
a
resu
l
t,
Γ
(
D
)
ν
ΓΓ
i
→
ν
j
+
γ
=
m
2
i
−
m
2
j
3
8
π
m
3
i
μ
D
i
j
2
+
D
i
j
2
=
9
α
em
G
2
F
m
5
i
2
11
π
4
1
−
m
2
j
m
2
i
3
1+
m
2
j
m
2
i
α
m
2
α
M
2
W
M
M
V
αi
VV
V
∗
αj
VV
2
(
3.87
)
f
or Dirac neutrinos
(
Lee and Shrock, 1977; Marciano and Sanda, 1977
;
Shrock, 1982; Pal and Wolfenstein, 1982
)
;or
Γ
(
M
)
ν
ΓΓ
i
→
ν
j
+
γ
=
m
2
i
−
m
2
j
3
8
π
m
3
i
μ
M
i
j
2
+
M
i
j
2
=
9
α
em
G
2
F
m
5
i
2
10
π
4
1
−
m
2
j
m
2
i
3
⎧
⎨
⎧⎧
⎩
⎨
⎨
1+
m
j
m
i
2
α
m
2
α
M
2
W
MM
Im
V
αi
VV
V
∗
αj
VV
2
+
1
−
m
j
m
i
2
α
m
2
α
M
2
W
MM
R
e
V
αi
VV
V
∗
αj
VV
2
⎫
⎬
⎫
⎫
⎭
⎬⎬
(
3.88
)
f
or Majorana neutrinos
(
Shrock, 1982
)
,wher
e
α
em
=
e
2
/
(
4
π
)
denotes th
e
electromagnetic fine-structure constant.
T
ocom
p
ar
e
Γ
ν
Γ
Γ
i
→
ν
j
+
γ
w
ith the experimental data in a simpler wa
y
,on
e
m
ay define an effective magnetic dipole moment
μ
eff
≡
μ
ij
2
+
i
j
2
.
(
3.89
)
E
q.
(
3.86
)
can then be expressed as
Γ
ν
Γ
Γ
i
→
ν
j
+
γ
=
5
.
3
×
1
−
m
2
j
m
2
i
3
m
i
1
e
V
3
μ
eff
μ
B
2
s
−
1
.
(
3.90
)
A
lthoug
h
μ
eff
i
sextremel
y
small in some simple extensions of the SM like
the one discussed in Section 3.4.2, it could be sufficiently large in some mor
e
c
omplicated or exotic scenarios be
y
ond the
S
M, such as a class o
f
extra
-
d
imension models
(
Mohapatr
a
e
tal
.
,
2004
)
. Experimentally, radiative decay
s
of massive neutrinos can be constrained by seeing no emission of the photons
f
r
o
m
so
l
a
r
ν
e
a
n
d
r
eacto
r
ν
e
fl
uxes. Much stron
g
er constraints on
μ
eff
ca
n
be
obtained from the Supernova 1987A limit on the neutrino decay and from the
a
strophysical limit on distortions of the cosmic microwave background
(
CMB
)
radiation
(
Raffelt, 1996, 1999
)
, as shown in Fig. 3.9. A brief summary of thes
e
l
imits is
(
Raffelt, 1999; Giunti and Studenikin, 2009
)
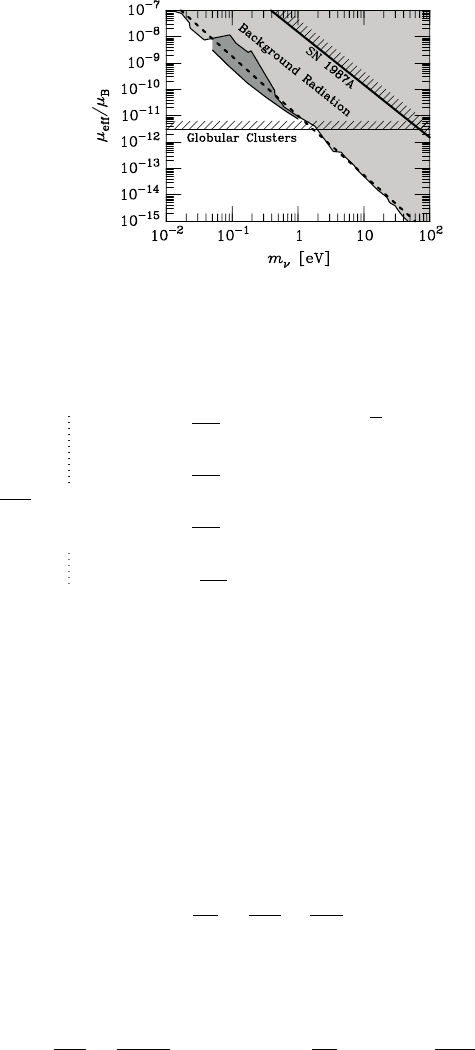
94 3 Neutrinos beyond the
S
tandard Mode
l
Fig. 3.9 Astrophysical bounds on the effective magnetic dipole momen
t
μ
e
ff
i
n
radiative neutrino decays
(
Raffelt, 1996, 1999. With permission from the University
of Chicago Press and Elsevier
)
μ
eff
μ
B
<
⎧
⎪
⎧⎧
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪
⎪
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪⎪
⎨
⎪⎪
⎪
⎨⎨
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪⎪
⎪
⎪⎪
⎩
⎪⎪
0
.
9
×
10
−
1
e
V
m
ν
2
Reactor
(
ν
e
)
,
0
.
5
×
1
0
−
5
e
V
m
ν
2
S
un
(
ν
e
)
,
1
.
5
×
10
−
8
eV
m
ν
2
S
N 1987A
(
all flavors
)
,
1
.
0
×
10
−
11
eV
m
ν
9
/
4
C
MB
(
all flavors
)
,
(
3.91
)
i
n
wh
i
ch
m
ν
is used to denote the e
ff
ective mass o
f
the decayin
g
neutrin
o
(
i.e.
,
m
ν
=
m
i
)
.
3.4.4 Electroma
g
netic Neutrino-electron Scatterin
g
In practice, the most sensitive way o
f
probin
g
the electroma
g
neticdipolemo
-
me
n
ts of a
m
ass
i
ve
n
eut
rin
o
i
sto
m
easu
r
et
h
ec
r
oss sect
i
o
n
of e
l
ast
i
c
n
eut
rin
o
-
electron
(
or antineutrino-electron
)
scattering, which can be expressed as a
s
um of the contribution from the SM
(
σ
0
)
and that from the electromagnetic
d
ipole moments of massive neutrinos
(
σ
μ
):
d
σ
d
T
=
d
σ
0
d
T
+
d
σ
μ
d
T
,
(
3.92
)
w
h
ere T
=
E
e
−
m
e
d
enotes the kinetic energy of the recoil electron in thi
s
process. Fo
ll
owin
g
t
h
eca
l
cu
l
ations
d
one in section 2.2.1, we
h
av
e
d
σ
0
d
T
=
G
2
F
m
e
2
π
g
2
+
+
g
2
−
1
−
T
E
ν
2
−
g
+
g
−
m
e
T
E
2
ν
(
3.93
)
3.4 Electromagnetic Properties o
f
Massive Neutrinos 9
5
f
or neutrino-electron scattering
(
’t Hooft, 1971; Marciano and Parsa, 2003
)
,
where
g
+
=
2s
in
2
θ
w
+
1for
ν
e
,
g
+
=2s
i
n
2
θ
w
−
1
for
ν
μ
a
nd
ν
τ
,
an
d
g
−
=
2
s
i
n
2
θ
w
f
or all flavors. Note that Eq.
(
3.93
)
is also valid for antineutrino-
electron scattering if one simply exchanges the positions o
f
g
+
a
n
d
g
−
.
O
n
the other hand
(
Bardin
et al
.
,
1970; Kyuldjiev, 1984; Vogel and Engel, 1989
),
d
σ
μ
d
T
=
α
2
em
π
m
2
e
1
T
−
1
E
ν
μ
ν
μ
B
2
(
3.94
)
w
i
th
μ
2
ν
≡|
μ
D
ii
|
2
+
|
D
ii
|
2
(
fo
r
i
=
1, 2 or 3
)
, which holds for both neutrino
s
a
nd antineutrinos. In obtaining Eqs.
(
3.93
)
and
(
3.94
)
one has assumed the
s
cattered neutrino to be a Dirac particle and omitted the effects of finit
e
n
eutrino masses and flavor mixing
(
i.e.
,
ν
e
=
ν
1
,
ν
μ
=
ν
2
a
n
d
ν
τ
=
ν
3
have
been taken
)
. Hence there is no interference between the contributions coming
f
rom the SM and electromagnetic dipole moments — the latter leads to a
h
elicity
fl
ip o
f
the neutrino but the
f
ormer is always helicity-conservin
g
. While
a
n interference term will a
pp
ear if one takes account of neutrino masses an
d
fl
avor mixin
g
,itsma
g
nitude linearly depends on the neutrino masses and thu
s
i
sstron
g
ly suppressed in comparison with the pure weak and electroma
g
neti
c
terms
(
Grimus and Stockinger, 1998
)
. So the incoherent sum o
f
d
σ
0
d
T
a
n
d
d
σ
μ
d
T
i
nEq.
(
3.92
)
is actually an excellent approximation of
d
σ
d
T
.
It
i
sobv
i
ous t
h
at t
h
etwote
rm
sof
d
σ
d
T
d
epend on the kinetic ener
g
yo
f
the
recoil electron in quite di
ff
erent ways. In particular,
d
σ
μ
d
T
g
rows rapi
dl
ywit
h
d
ecreasing values of
T
.
Hence a measurement of smaller T can pro
b
esma
ll
e
r
μ
ν
in this kind of experiments. The ma
g
nitude of
d
σ
μ
d
T
b
ecomes lar
g
er than
t
h
at of
d
σ
0
d
T
if t
h
eco
n
d
i
t
i
on
T
α
2
em
π
2
G
2
F
m
3
e
μ
ν
μ
B
2
≈
3
×
10
22
μ
ν
μ
B
2
keV
(
3.95
)
i
s roughly satisfied, as one can easily see from Eqs.
(
3.93
)
and
(
3.94
)
.N
o
d
istortion of the recoil electron energy spectrum o
f
ν
α
e
−
or
ν
α
e
−
s
catterin
g
(
fo
r
α
=
e
,
μ
,τ
)
has so far been observed in any direct laboratory experiments,
a
nd thus onl
y
the upper bounds o
n
μ
ν
can be derived
(
Wong and Li, 2005;
B
eda
et al
.
,
2007
)
. For instance, an analysis of the
T
-spectrum in the
S
K
experiment
y
ield
s
μ
ν
<
1
.
1
×
10
−
1
0
μ
B
(
Li
u
et al.
, 2004
)
; several recent reacto
r
ex
p
eriments o
n
ν
e
e
−
scattering yield
μ
ν
<
⎧
⎨
⎧⎧
⎩
⎨⎨
9
.
0
×
10
−
11
μ
B
MUNU
(
Darakchieva
et al
.,
2
005
)
,
7
.
4
×
1
0
−
1
1
μ
B
TEXONO
(
Won
g
et al
.,
2007
)
,
5
.
8
× 1
0
−
1
1
μ
B
G
EMMA
(
Beda et a
l
.
,
2007
)
;
(
3.96
)
