Xing Zh., Zhou Sh. Neutrinos in Particle Physics, Astronomy and Cosmology
Подождите немного. Документ загружается.


76 3 Neutrinos beyond the
S
tandard Mode
l
−L
h
y
brid
=
ν
L
M
D
MM
N
R
NN
+
1
2
ν
L
M
L
MM
(
ν
L
)
c
+
1
2
(
N
R
NN
)
c
M
R
MM
N
R
NN
+h
.
c
.
=
1
2
ν
L
(
N
R
NN
)
c
M
L
MM
M
D
MM
M
T
D
MM
M
R
MM
(
ν
L
)
c
N
R
NN
+h
.
c
.,
(
3.30
)
where
M
L
MM
a
nd
M
R
MM
a
re symmetric mass matrices because the corresponding
m
ass terms are o
f
the Majorana type, and the relationship
(
N
R
NN
)
c
M
T
D
MM
(
ν
L
)
c
=
(
N
R
NN
)
T
C
M
T
D
MM
C
ν
L
T
T
=
ν
L
M
D
MM
N
R
NN
(
3.31
)
h
as
b
een use
d
.T
h
eovera
ll 6
×
6
mass matrix in Eq.
(
3.30
)
is also symmetri
c
a
nd can be dia
g
onalized by a
6
×
6 unitary matrix throu
g
h the trans
f
ormation
VR
S
U
†
M
L
MM
M
D
MM
M
T
D
MM
M
R
MM
VR
SU
∗
=
$
M
ν
MM
0
0
$
M
N
M
,
(
3.32
)
whe
r
e
$
M
ν
MM
≡
D
ia
g
{
m
1
,m
2
,
m
3
}
,
$
M
N
M
≡
D
ia
g
{
M
1
,M
2
MM
,M
3
MM
}
,an
d
t
h
e3
×
3
s
ub-matrice
s
V
,
R
,
S
a
nd
U
s
atisf
y
the unitarit
y
condition
s
VV
†
+
RR
†
=
SS
†
+
UU
†
=
1
,
V
†
V
+
S
†
S
=
R
†
R
+
U
†
U
=
1
,
V
S
†
+
R
U
†
=
V
†
R
+
S
†
U
=
0 .
(
3.33
)
A
fter this diagonalization, Eq.
(
3.30
)
becomes
−
L
h
y
b
ri
d
=
1
2
ν
L
(
N
R
NN
)
c
$
M
ν
MM
0
0
$
M
N
M
(
ν
L
)
c
N
R
NN
+
h
.
c
.,
(
3.34
)
w
h
ere
ν
L
=
V
†
ν
L
+
S
†
(
N
R
NN
)
c
an
d
N
R
NN
=
R
T
(
ν
L
)
c
+
U
T
N
R
NN
t
oget
h
er wit
h
(
ν
L
)
c
=
C
ν
L
T
and
(
N
R
NN
)
c
=
C
N
R
NN
T
.
Th
e
n
t
h
efie
l
d
ν
=
ν
L
(
N
R
NN
)
c
+
(
ν
L
)
c
N
R
NN
=
⎛
⎜
⎛⎛
⎜
⎜⎜
⎜
⎜⎜
⎜
⎜⎜
⎜
⎜⎜
⎜
⎜⎜
⎝
⎜⎜
ν
1
ν
2
ν
3
N
1
NN
N
2
NN
N
3
NN
⎞
⎟
⎞⎞
⎟
⎟⎟
⎟
⎟⎟
⎟
⎟⎟
⎟
⎟⎟
⎟
⎟⎟
⎠
⎟⎟
(
3.35
)
s
atisfies the Majorana condition
(
ν
)
c
=
ν
an
dd
escri
b
es t
h
e mass eigenstates
o
f
six Ma
j
orana neutrinos. In other words
,
−L
hy
brid
=
1
2
ν
$
M
ν
MM
0
0
$
M
N
M
ν
=
1
2
3
i
=
1
m
i
ν
i
ν
i
+
M
i
MM
N
i
NN
N
i
NN
.
(
3.36
)
Because o
f
ν
L
=
Vν
L
+
R
(
N
R
N
N
)
c
an
d
N
R
N
N
=
S
∗
(
ν
L
)
c
+
U
∗
N
R
N
N
,
we imme
d
iate
l
y
h
ave
(
ν
L
)
c
=
V
∗
(
ν
L
)
c
+
R
∗
N
R
N
N
and
(
N
R
NN
)
c
=
Sν
L
+
U
(
N
R
NN
)
c
.
G
iven the re
-
lat
i
o
n
s
(
ψ
L
)
c
γ
μ
∂
μ
(
ψ
L
)
c
=
ψ
L
γ
μ
∂
μ
ψ
L
a
n
d
(
ψ
R
)
c
γ
μ
∂
μ
(
ψ
R
)
c
=
ψ
R
γ
μ
∂
μ
ψ
R
fo
r
a
n arbitrary fermion field
ψ
, the kinetic term of Majorana neutrinos reads

3.2 Dirac an
d
Majorana Neutrino Mass Terms 7
7
L
k
ineti
c
=i
ν
L
γ
μ
∂
μ
ν
L
+i
N
R
NN
γ
μ
∂
μ
N
R
NN
=
i
2
ν
L
(
N
R
NN
)
c
γ
μ
∂
μ
ν
L
(
N
R
NN
)
c
+
i
2
(
ν
L
)
c
N
R
NN
γ
μ
∂
μ
(
ν
L
)
c
N
R
NN
=
i
2
ν
L
(
N
R
NN
)
c
γ
μ
∂
μ
VR
S
U
†
VR
S
U
ν
L
(
N
R
NN
)
c
+
i
2
(
ν
L
)
c
N
R
N
N
γ
μ
∂
μ
VR
SU
T
V
R
SU
∗
(
ν
L
)
c
N
R
NN
=
i
2
ν
L
(
N
R
N
N
)
c
γ
μ
∂
μ
ν
L
(
N
R
NN
)
c
+
i
2
(
ν
L
)
c
N
R
N
N
γ
μ
∂
μ
(
ν
L
)
c
N
R
NN
=i
ν
L
γ
μ
∂
μ
ν
L
+
i
N
R
NN
γ
μ
∂
μ
N
R
NN
=
i
2
ν
γ
μ
∂
μ
ν
=
i
2
3
k
=1
ν
k
γ
μ
∂
μ
ν
k
+
N
k
N
γ
μ
∂
μ
N
k
N
,
(
3.37
)
where the unitarity conditions given in Eq.
(
3.33
)
have been used
.
T
he weak charged-current interactions of active neutrinos in Eq.
(
3.9
)
ca
n
n
ow be rewritten in terms of the mass eigenstates of six Majorana neutrinos
via
ν
L
=
V
ν
L
+
R
(
N
R
NN
)
c
.In
t
h
ec
h
ose
n
bas
i
sw
h
e
r
et
h
eflavo
r
a
n
d
m
ass
ei
g
enstates of three char
g
ed leptons are identical, we have
L
cc
=
g
√
2
(
eμτ
)
L
γ
μ
⎡
⎣
V
⎛
⎝
⎛
⎛
ν
1
ν
2
ν
3
⎞
⎠
⎞
⎞
L
+
R
⎛
⎝
⎛
⎛
N
1
NN
N
2
NN
N
3
NN
⎞
⎠
⎞
⎞
L
⎤
⎦
W
−
μ
W
+h
.
c
..
(
3.38
)
Note that
V
a
n
d
R
a
re responsible
f
or the char
g
ed-current interactions o
f
t
hr
ee
kn
ow
nn
eut
rin
os
ν
i
a
n
dt
hr
ee
n
ew
n
eut
rin
os
N
i
NN
(
fo
r
i
=1
,
2
,
3
)
,re-
s
pectively. Their correlation is described by
VV
†
+
RR
†
=
1
,
and thu
s
V
i
s not unitary un
l
ess
ν
i
a
n
d
N
i
NN
are completely decoupled
(
i.e.
,
R
=
0
)
.
A
p
arametrization o
f
V
a
nd
R
in terms of some mixin
g
an
g
les and CP-violatin
g
phases will be presented in section 4.5.2
(
Xing, 2008b
)
.
A
s a consequence of lepton number violation, the
0
ν
2
β
decay
(
A
,
Z
)
→
(
A,
Z
+
2
)
+2
e
−
can now take place via the exchan
g
es of bot
h
ν
i
a
nd
N
i
N
N
b
etween two
b
eta
d
ecays, w
h
ose coup
l
ing matrix e
l
ements ar
e
V
ei
VV
a
n
d
R
e
i
respectivel
y
. The relative contributions o
f
ν
i
a
n
d
N
i
NN
to t
h
is
l
epton-num
b
er-
violating process depend not only on
m
i
,
M
i
MM
,
V
ei
VV
an
d
R
ei
but also on the
relevant nuclear matrix elements which cannot be reliably evaluated
(
Haxto
n
a
nd Stephenson, 1984
)
. For a realistic seesaw mechanism working at the Te
V
s
cale
(
i.e.
,
M
i
MM
∼O
(
1
)
TeV
)
or at a superhigh-energy scale, however, the
co
n
t
ri
but
i
o
n
o
f
ν
i
t
ot
h
e
0
ν
2
β
d
ecay is in most cases dominant
(
Xing, 2009b
)
.
T
he hybrid neutrino mass terms in Eq.
(
3.30
)
provide us with the neces
-
s
ary ingredients of a dynamic mechanism to interpret why three known neu
-
trinos
h
ave nonzero
b
ut tiny masses. T
h
e
k
ey point is t
h
at t
h
e mass sca
l
es
of
M
L
MM
,
M
D
MM
a
n
d
M
R
MM
m
ay have a stron
g
hierarchy. First,
M
D
MM
∼
H
≈
1
7
4
GeV is naturally characterized by the electroweak symmetry breaking scale
.

78 3 Neutrinos beyond the
S
tandard Mode
l
S
econd,
M
L
MM
H
s
atisfies ’t Hooft’s naturalness criterion
(
’t Hooft, 1980
)
because this Ma
j
orana mass term violates lepton number conservation. Third
,
M
R
MM
H
is natura
ll
y expecte
d
since rig
h
t-
h
an
d
e
d
neutrinos are
SU
(
2
)
L
g
au
g
esin
gl
ets an
d
t
h
us t
h
eir mass term is not su
b
ject to t
h
ee
l
ectrowea
k
s
ymmetry breakin
g
scale. The hierarch
y
M
R
MM
M
D
MM
M
L
MM
can therefore al-
l
ow us to make reliable approximations in deriving the effective mass matri
x
ofthreeactiveneutrinos
(
ν
e
,
ν
μ
,ν
τ
)
from Eq.
(
3.32
)
. The latter yield
s
R
$
M
N
M
=
M
L
MM
R
∗
+
M
D
MM
U
∗
,
S
$
M
ν
MM
=
M
T
D
MM
V
∗
+
M
R
MM
S
∗
;
(
3.39
)
a
n
d
U
$
M
N
M
=
M
R
MM
U
∗
+
M
T
D
MM
R
∗
,
V
$
M
ν
MM
=
M
L
MM
V
∗
+
M
D
MM
S
∗
.
(
3.40
)
G
ive
n
M
R
MM
M
D
MM
M
L
MM
,
R
∼
S
∼
O
(
M
D
MM
/M
R
MM
)
naturally holds, implying
tha
t
U
an
d
V
a
re almost unitar
y
up to the accurac
y
o
f
O
(
M
2
D
MM
/M
2
R
MM
)(
Xing
a
nd Zhou, 2006
)
. Hence Eq.
(
3.40
)
leads to
U
$
M
N
M
U
T
=
M
R
MM
(
UU
†
)
T
+
M
T
D
MM
(
R
∗
U
T
)
≈
M
R
MM
,
V
$
M
ν
MM
V
T
=
M
L
MM
(
VV
†
)
T
+
M
D
MM
(
S
∗
V
T
)
≈
M
L
MM
+
M
D
MM
(
S
∗
V
T
)
.
(
3.41
)
Note that
S
∗
V
T
=
M
−
1
R
MM
S
$
M
ν
MM
V
T
−
M
−
1
R
MM
M
T
D
M
M
(
VV
†
)
T
≈
−
M
−
1
R
MM
M
T
D
MM
ca
n
be
d
erived from Eq.
(
3.39
)
. We substitute this expression into Eq.
(
3.41
)
and
the
n
obta
i
n
M
ν
MM
≡
V
$
M
ν
MM
V
T
≈
M
L
MM
−
M
D
MM
M
−
1
R
MM
M
T
D
MM
.
(
3.42
)
This result, known as the type-
(
I+II
)
seesaw relation, is just the effective mas
s
m
atrix of three light neutrinos. The small mass scale of
M
ν
MM
i
satt
ri
buted to
t
h
es
m
a
ll m
ass sca
l
eof
M
L
MM
and the lar
g
emassscaleo
f
M
R
MM
.T
he
r
ea
r
etwo
particularly interesting limits
.
•
If t
h
e
m
ass te
rm
M
L
MM
is absent from Eq.
(
3.30
)
, one will be left with the
canonical or t
y
pe-I seesaw relatio
n
M
ν
MM
≈−
M
D
MM
M
−
1
R
MM
M
T
D
MM
(
Fritzsch et al.
,
1975; Minkowski, 1977; Yanagida, 1979; Gell-Man
n
et al.
, 1979; Glashow
,
1980; Mohapatra and Senjanovic, 1980
)
.
•
I
fonl
y
themasster
m
M
L
M
M
is present in Eq.
(
3.30
)
, one will be left wit
h
th
e type-II seesaw re
l
ation
M
ν
MM
=
M
L
MM
(
Konetschny and Kummer, 1977;
M
a
gg
and Wetterich, 1980;
S
chechter and Valle, 1980;
C
hen
g
and Li, 1980;
Lazaride
s
et al., 1981; Mohapatra and Senjanovic, 1981
)
.
More
d
etai
l
e
dd
iscussions a
b
out various seesaw mec
h
anisms an
d
t
h
eir p
h
e
-
n
omenolo
g
ical consequences will be presented in Chapter 4
.
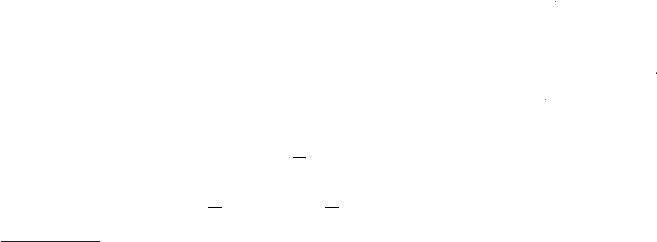
3.3
C
, P and T Properties o
f
Fermion Fields 79
3
.3 C, P and T Properties of Fermion Field
s
CP violation is one of a few central concepts in flavor physics. The phe
-
n
omenon o
fC
P violation was
fi
rst observed b
y
James
C
ronin and Val Fitch
i
n the deca
y
mod
e
K
L
→
π
+
π
−
(
Christenso
n
et al
.
, 1964
)
. Large CP-violatin
g
effects were predicted to appear in a variety of
B
-
meson
d
ecays
b
ase
d
on t
he
K
obayashi-Maskawa mechanism of CP violation within the SM
(
Kobayash
i
a
nd Maskawa, 1973
)
, and they were observed to a good degree of accuracy a
t
B
-
meson factories
(
Auber
t
et al
.
,
2001; Ab
e
et al.
,
2001
)
. Nevertheless, th
e
m
a
g
nitude o
fC
P violation in the quark sector is insu
ffi
cient to account
f
or
the cosmological matter-antimatter asymmetry. Hence one wonders whether
there is
C
P violation in the lepton sector and whether it can account
f
or
the observed bar
y
on-antibar
y
on as
y
mmetr
y
o
f
the Universe. We shall see i
n
Chapter 11 that it is possible to realize baryogenesis via leptogenesis thanks
to
C
P violation in the neutrino sector
,
I
n this section we shall first discuss the C, P, T, CP and CPT
p
ro
p
erties
of quark and lepton fields, and then diagnose both the origin of CP violatio
n
i
n the quark sector o
f
the
S
M and that in the lepton sector
f
or a minima
l
extension of the SM to accommodate finite neutrino masses. It will be demon
-
s
trated that CP violation arises from the coexistence of the charged-curren
t
i
n
te
r
act
i
o
n
soffe
rmi
o
n
sw
i
t
h
t
h
e
W
±
boso
n
sa
n
dt
h
e
Y
u
k
awa
in
te
r
act
i
o
n
sof
f
ermions with the Higgs boson.
3.3.1 C, P and T Trans
f
ormations o
f
Spinor Bilinears
We be
g
in with a brie
f
summary o
f
the trans
f
ormation properties o
f
quantum
fields under the discrete space-time symmetries of parity
(
P
)
,chargecon
-
j
ugation
(
C
)
and time reversal
(
T
)
. The parity transformation changes the
s
pace coor
d
inates
x
i
n
to
−
x
.
The char
g
e conju
g
ation
fl
ips the si
g
ns o
f
inter
-
n
al charges of a particle, such as the electric charge and the lepton
(
baryon
)
nu
m
be
r. Th
et
im
e
r
eve
r
sa
lr
e
fl
ects t
h
et
im
ecoo
r
d
in
ate
t
in
to
−
t
.
T
he t
r
a
n
s-
f
ormation properties of scalar
(
S
)
, pseudoscalar
(
P
)
, vector
(
V
μ
VV
)
and pseu-
d
ovector
(
A
μ
)
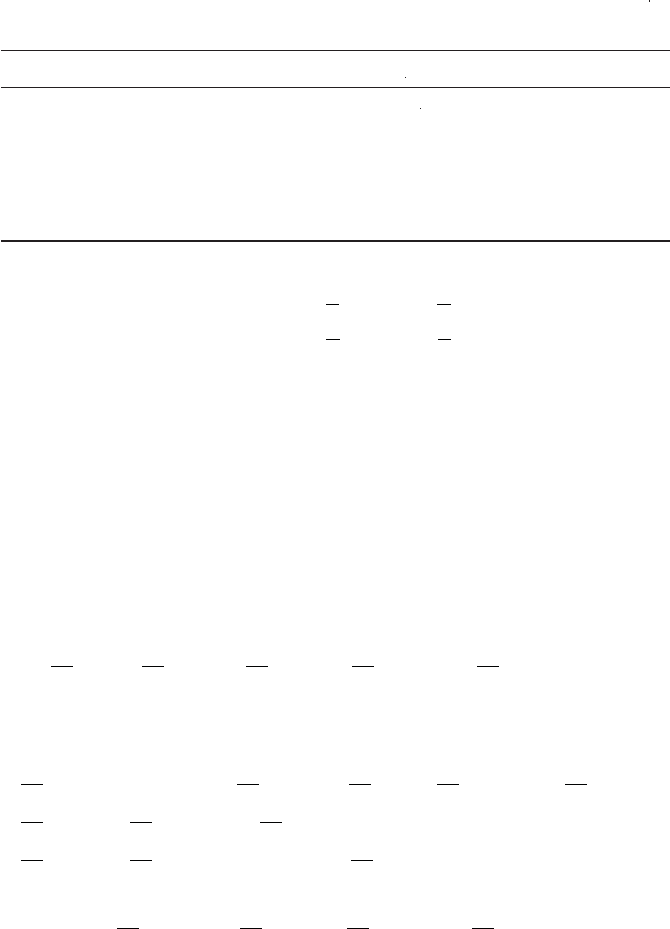
fields under C, P and T, which are summarized in Table 3.4,
h
ave been discussed in detail in some literature
(
Jarlskog, 1989; Peskin an
d
S
chroeder, 1995; Branco
et al.
,
1999; Bigi and Sanda, 2000
)
. Note tha
t
V
μ
V
V
a
nni
h
i
l
ates a vector partic
l
ean
d
creates its antipartic
l
e, w
h
i
le
V
†
μ
VV
d
oes t
h
eop
-
posite operation. So d
o
S
,
P
,
A
μ
a
n
d
S
†
,
P
†
,
A
†
μ
.
Hence the roles of particles
a
nd antiparticles are interchan
g
ed under
C.
A free Dirac s
p
ino
r
ψ
(
t,
x
)
o
r
ψ
(
t,
x
)
transforms under C, P and T a
s
4
ψ
(
t,
x
)
C
−→ C
C
ψ
T
(
t,
x
)
,
ψ
(
t
,
x
)
C
−→
−
ψ
T
(
t
,
x
)
C
−
1
,
4
F
or simplicity, here we have omitted a phase factor associated with each trans-
f
ormation. Because one is alwa
y
s interested in the spinor bilinears, the relevant
phase factor usually plays no physical role.
80 3 Neutrinos beyond the
S
tandard Mode
l
Table 3.4 Transformation properties of scalar
(
S
)
, pseudoscalar
(
P
)
,vector
(
V
μ
VV
)
and pseudovector
(
A
μ
)
fields under C, P and
T
S
(
t
,
x
)
P
(
t,
x
)
V
μ
VV
(
t,
x
)
A
μ
(
t
,
x
)
C
S
†
(
t,
x
)
P
†
(
t,
x
)
−
V
†
μ
VV
(
t,
x
)
A
†
μ
(
t,
x
)
P
S
(
t,
−
x
)
−
P
(
t
,
−
x
)
V
μ
(
t
,
−
x
)
−
A
μ
(
t,
−
x
)
T
S
(
−
t
,
x
)
P
(
−
t
,
x
)
V
μ
(
−
t
,
x
)
A
μ
(
−
t
,
x
)
CP
S
†
(
t,
−
x
)
−
P
†
(
t,
−
x
)
−
V
μ
†
(
t,
−
x
)
−
A
μ
†
(
t,
−
x
)
C
PT
S
†
(
−
t
,
−
x
)
−
P
†
(
−
t
,
−
x
)
−
V
†
μ
VV
(
−
t
,
−
x
)
−
A
†
μ
(
−t,
−
x
)
ψ
(
t,
x
)
P
−→ P
P
ψ
(
t,
−
x
)
,
ψ
(
t,
x
)
P
−→
ψ
(
t
,
−
x
)
P
†
,
ψ
(
t,
x
)
T
−→ T
T
ψ
(
−
t
,
x
)
,
ψ
(
t,
x
)
T
−→
ψ
(
−
t
,
x
)
T
†
,
(
3.43
)
w
h
e
r
e
C
=i
γ
2
γ
0
,
P
=
γ
0
a
n
d
T
=
γ
1
γ
3
i
n the Dirac-Pauli re
p
resentation.
These transformation properties can simply be deduced from the require
-
m
ent t
h
at t
h
e Dirac equation
i
γ
μ
∂
μ
ψ
(
t
,
x
)
=
mψ
(
t,
x
)
be invariant under
C, P or T operation. Note that all the classical numbers
(
or c-numbers
),
s
uc
h
as t
h
e coup
l
ing constants an
d
γ
-
matrix e
l
ements, must
b
e comp
l
ex
-
c
onju
g
ate
d
un
d
er T. Note a
l
so t
h
at t
h
ec
h
ar
g
e-conju
g
ation matrix
C
sat
i
sfies
the conditions given in Eq.
(
3.8
)
. It is very important to figure out how the
D
irac spinor bilinears transform under C, P and T, because both leptons and
q
uarks are described b
y
spinor
fi
elds and the
y
alwa
y
s appear in the bilinear
f
orms in a Lorentz-invariant Lagrangian. Let us consider the following scalar-,
pseu
d
osca
l
ar-, vector-, pseu
d
ovector- an
d
tensor-
l
i
k
e spinor
b
i
l
inears
:
ψ
1
ψ
2
,
i
ψ
1
γ
5
ψ
2
,
ψ
1
γ
μ
ψ
2
,
ψ
1
γ
μ
γ
5
ψ
2
,
ψ
1
σ
μν
ψ
2
,
(
3.44
)
where
σ
μν
≡
i[
γ
μ
,γ
ν
]
/
2
is defined. One ma
y
easil
y
verif
y
that all these bilin-
ears are Hermitian, if
ψ
1
=
ψ
2
is taken. Under C, P and T, for example
,
ψ
1
γ
μ
ψ
2
C
−
→−
ψ
T
1
C
−
1
γ
μ
C
ψ
2
T
=
ψ
T
1
γ
T
μ
ψ
2
T
=
−
ψ
2
γ
μ
ψ
1
T
=
−
ψ
2
γ
μ
ψ
1
,
ψ
1
γ
μ
ψ
2
P
−
→
ψ
1
γ
0
γ
μ
γ
0
ψ
2
=
ψ
1
γ
μ
ψ
2
,
ψ
1
γ
μ
ψ
2
T
−
→
ψ
1
(
γ
1
γ
3
)
†
γ
∗
μ
(
γ
1
γ
3
)
ψ
2
=
ψ
1
γ
μ
ψ
2
;
(
3.45
)
a
n
dthus
ψ
1
γ
μ
ψ
2
C
P
−
→
−
ψ
2
γ
μ
ψ
1
,
ψ
1
γ
μ
ψ
2
C
P
T
−
→−
ψ
2
γ
μ
ψ
1
,
(
3.46
)
wit
h
x
→−
x
un
d
er P an
d
t
→−
t
under T fo
r
ψ
1
a
n
d
ψ
2
.
The transformatio
n
properties o
ffi
ve spinor bilinears under
C
,P,T,
C
Pand
C
PT are summa-
rized in Table 3.5, where one should kee
p
in mind that all the c-numbers ar
e
c
omplex-conjugated under T and CPT. Comparing between Table 3.4 an
d

3.3
C
, P and T Properties o
f
Fermion Fields 81
Ta
bl
e 3.5, we arrive at
S
(
t
,
x
)
=
ψ
1
(
t
,
x
)
ψ
2
(
t
,
x
)
,
P
(
t,
x
)=
ψ
1
(
t
,
x
)
γ
5
ψ
2
(
t,
x
),
V
μ
V
V
(
t
,
x
)
=
ψ
1
(
t
,
x
)
γ
μ
ψ
2
(
t,
x
)
an
d
A
μ
(
t
,
x
)
=
ψ
1
(
t,
x
)
γ
μ
γ
5
ψ
2
(
t
,
x
)
, corre-
s
ponding to scalar, pseudoscalar, vector and pseudovector fields. Note tha
t
ψ
(
t,
x
)
γ
5
ψ
(
t,
x
)
itself is not Hermitian, but i
ψ
(
t
,
x
)
γ
5
ψ
(
t
,
x
)
is Hermitian just
because it contains i
.
Table 3.5 Trans
f
ormation
p
ro
p
erties o
f
the scalar-,
p
seudoscalar-, vector-,
pseudovector- and tensor-like spinor bilinears under C, P and T. Her
e
x →−
x
under P,
C
Pand
C
PT, to
g
ether with
t
→
−
t
u
nder T and
C
PT
,
is hidden and
sel
f
-explainin
gf
o
r
ψ
1
an
d
ψ
2
ψ
1
ψ
2
i
ψ
1
γ
5
ψ
2
ψ
1
γ
μ
ψ
2
ψ
1
γ
μ
γ
5
ψ
2
ψ
1
σ
μν
ψ
2
C
ψ
2
ψ
1
i
ψ
2
γ
5
ψ
1
−
ψ
2
γ
μ
ψ
1
ψ
2
γ
μ
γ
5
ψ
1
−
ψ
2
σ
μν
ψ
1
P
ψ
1
ψ
2
−
i
ψ
1
γ
5
ψ
2
ψ
1
γ
μ
ψ
2
−
ψ
1
γ
μ
γ
5
ψ
2
ψ
1
σ
μν
ψ
2
T
ψ
1
ψ
2
−
i
ψ
1
γ
5
ψ
2
ψ
1
γ
μ
ψ
2
ψ
1
γ
μ
γ
5
ψ
2
−
ψ
1
σ
μν
ψ
2
CP
ψ
2
ψ
1
−
i
ψ
2
γ
5
ψ
1
−
ψ
2
γ
μ
ψ
1
−
ψ
2
γ
μ
γ
5
ψ
1
−
ψ
2
σ
μν
ψ
1
C
PT
ψ
2
ψ
1
i
ψ
2
γ
5
ψ
1
−
ψ
2
γ
μ
ψ
1
−
ψ
2
γ
μ
γ
5
ψ
1
ψ
2
σ
μν
ψ
1
I
t is well known that CPT is a good symmetry in a local quantu
m
fi
eld theory which is Lorentz-invariant and possesses a Hermitian La
g
ran
g
ia
n
(
Schwinger, 1951; L¨uders, 1954; Pauli, 1955
)
. The latter is necessary in order
to have a unitary transition operator
(
i.e., the
S
-
matrix
)
. The CPT invari
-
a
nce o
f
a theory implies that
C
P and T must be simultaneously conservin
g
or broken, as alread
y
examined in the quark sector of the SM via the
K
0
-
¯
K
0
m
ixing system
(
Nakamur
a
et al
., 2010
)
. After a slight modification of th
e
S
M by introducin
g
the Dirac or Majorana mass term
f
or three neutrinos, one
m
ay also look at possible sources of CP or T violation in the lepton sector
.
3.3.2 CP Violation in Quark and Lepton Sector
s
A
s discussed in Cha
p
ter 2, the SM of electroweak interactions is based o
n
the
SU
(
2
)
L
×
U
(
1
)
Y
g
auge symmetry an
d
t
h
e Higgs mec
h
anism. T
h
e
l
atte
r
tri
gg
ers t
h
e spontaneous symmetry
b
rea
k
in
g
SU
(
2
)
L
×
U
(
1
)
Y
→
U
(
1
)
Q
,
suc
h
that three gauge bosons, three charged leptons and six quarks can all acquir
e
m
asses. But this mechanism itself does not spontaneously break CP, and thus
one ma
y
examine the source o
fC
P violation in the
S
Meitherbe
f
ore or a
f
ter
s
pontaneous symmetry breaking
.
T
he La
g
ran
g
ian o
f
the
S
M
L
=
L
G
+
L
H
+
L
F
+
L
Y
is composed o
ff
ou
r
parts: the kinetic term of the gauge fields and their self-interactions
(
L
G
)
,th
e
kinetic term of the Higgs doublet and its potential and interactions with the

82 3 Neutrinos beyond the
S
tandard Mode
l
gauge fields
(
L
H
)
, the kinetic term of the fermion fields and their interactions
with the gauge fields
(
L
F
)
, and the Yukawa interactions of the fermion fields
with the Higgs doublet
(
L
Y
):
L
G
=
−
1
4
W
iμν
W
i
μν
W
+
B
μν
B
μν
,
L
H
=(
D
μ
H
)
†
D
μ
H
−
μ
2
H
†
H
−
λ
H
†
H
2
,
L
F
=
Q
L
i
/
DQ
//
L
+
L
i
/
D
//
L
+
U
R
UU
i
/
∂
//
U
R
U
U
+
D
R
i
/
∂
//
D
R
+
E
R
i
/
∂
//
E
R
,
L
Y
=
−
Q
L
Y
u
YY
˜
HU
R
UU
−
Q
L
Y
d
Y
Y
HD
R
−
L
Y
l
YY
H
E
R
+h
.
c
.,
(
3.47
)
whose notations have been explained in Section 2.1.4. To accommodate finit
e
n
eutrino masses, the simplest way is to sli
g
htly modi
f
yth
e
L
F
a
n
d
L
Y
p
arts
of the SM
(
e.g., by introducing three right-handed neutrinos into the S
M
a
nd allowing for the Yukawa interactions between neutrinos and the Higg
s
d
oublet
)
. CP violation is due to the coexistence of
L
F
a
n
d
L
Y
.
W
e first show that
L
G
i
salwa
y
s invariant under CP. The transformation
properties o
fg
au
g
e
fi
elds
B
μ
a
n
d
W
i
μ
W
under
C
and P ar
e
B
μ
,W
1
μ
W
,W
2
μ
W
,W
3
μ
W
C
−→
−
B
μ
,
−
W
1
μ
W
,
+
W
2
μ
W
,
−
W
3
μ
W
,
B
μ
,W
1
μ
W
,W
2
μ
W
,W
3
μ
W
P
−→
B
μ
,
W
1
μ
,W
2
μ
,
W
3
μ
,
B
μ
,W
1
μ
W
,W
2
μ
W
,W
3
μ
W
C
P
−→
−
B
μ
,
−
W
1
μ
,
+
W
2
μ
,
−
W
3
μ
(
3.48
)
wit
h
x
→
−
x
u
nder P and CP for relevant fields. Then the gauge field tensors
B
μν
a
n
d
W
i
μν
W
t
ransform under
C
P as follows
:
B
μν
,W
1
μν
W
,W
2
μν
W
,W
3
μν
W
CP
−
→
−
B
μν
,
−
W
1
μν
,
+
W
2
μν
,
−
W
3
μν
.
(
3.49
)
He
n
ce
L
G
i
s formally invariant under CP.
W
e procee
d
to s
h
ow t
h
a
t
L
H
i
s also invariant under
C
P. The Hi
gg
s doublet
H
c
ontains two scalar com
p
onents
φ
+
and
φ
0
;
i.e.
,
H
=
φ
+
φ
0
,H
†
=
φ
−
φ
0
∗
.
(
3.50
)
O
ne can directly read o
ff
the trans
f
ormation properties o
f
φ
±
a
n
d
φ
0
u
n
der
C
P
f
rom Table 3.4. There
f
ore
,
H
(
t
,
x
)
C
P
−→
H
∗
(
t,
−
x
)=
φ
−
φ
0
∗
.
(
3.51
)
It is ver
y
trivial to prove that th
e
H
†
H
a
nd
(
H
†
H
)
2
terms of
L
H
are CP-
i
nvariant. To examine how the
(
D
μ
H
)
†
(
D
μ
H
)
term of
L
H
t
r
a
n
s
f
o
rm
su
n
de
r
C
P, we explicitl
y
write ou
t
3.3
C
, P and T Properties o
f
Fermion Fields 83
D
μ
H
=
∂
μ
−
i
g
τ
k
W
k
μ
W
−
i
g
YB
μ
H
=
∂
μ
φ
+
−
i
X
+
μ
φ
0
−
i
Y
+
μ
YY
φ
+
∂
μ
∂
φ
0
−
i
X
−
μ
φ
+
+
i
Y
−
μ
YY
φ
0
(
3.52
)
w
i
th
X
±
μ
≡
gW
±
μ
W
/
√
2=
g
(
W
1
μ
W
∓
i
W
2
μ
W
)
/
2
a
n
d
Y
±
μ
YY
≡
±
g
YB
μ
+
gW
3
μ
W
/
2
.Th
e
n
(
D
μ
H
)
†
D
μ
H
=
∂
μ
φ
−
∂
μ
φ
+
−
i
∂
μ
φ
−
X
+
μ
φ
0
−
i
∂
μ
φ
−
Y
+
μ
YY
φ
+
+i
X
−
μ
φ
0
∗
∂
μ
φ
+
+
X
−
μ
X
+
μ
|
φ
0
|
2
+
X
−
μ
φ
0
∗
Y
+
μ
Y
Y
φ
+
+i
Y
+
μ
φ
−
∂
μ
φ
+
+
Y
+
μ
X
+
μ
φ
−
φ
0
+
Y
+
μ
Y
+
μ
Y
Y
|
φ
+
|
2
+
∂
μ
φ
0
∗
∂
μ
φ
0
−
i
∂
μ
φ
0
∗
X
−
μ
φ
+
+i
∂
μ
φ
0
∗
Y
−
μ
Y
Y
φ
0
+i
X
+
μ
φ
−
∂
μ
∂
φ
0
+
X
+
μ
X
−
μ
|
φ
+
|
2
−
X
+
μ
φ
−
Y
−
μ
YY
φ
0
−
i
Y
−
μ
φ
0
∗
∂
μ
φ
0
−
Y
−
μ
X
−
μ
φ
0
∗
φ
+
+
Y
−
μ
Y
−
μ
YY
|
φ
0
|
2
.
(
3.53
)
Note t
h
at
X
±
μ
CP
−
→
−
X
∓
μ
,Y
±
μ
YY
CP
−
→
−
Y
±
μ
,
(
3.54
)
toget
h
er wit
h
∂
μ
→
∂
μ
,
φ
±
→
φ
∓
an
d
φ
0
→
φ
0
∗
u
nder CP. So
(
D
μ
H
)
†
(
D
μ
H
)
i
salso
C
P-invariant. There
f
ore
,
L
H
is
f
ormall
y
invariant under
C
P.
T
he next ste
p
is to examine the CP invariance of
L
F
.Tobemores
p
ecific
,
we
d
ivi
de
L
F
i
nto t
h
equar
k
sector an
d
t
h
e
l
epton sector; i.e.
,
L
F
=
L
q
+
L
l
.
We onl
y
anal
y
ze the
C
P propert
y
o
f
L
q
in the
f
ollowin
g
, because that o
f
L
l
c
an be anal
y
zedinthesamewa
y
. The explicit form o
f
L
q
r
eads
L
q
=
Q
L
i
/
DQ
//
L
+
U
R
UU
i
/
∂
//
U
R
UU
+
D
R
i
/
∂
//
D
R
=
3
j
=
1
q
j
q
q
j
q
L
i
γ
μ
∂
μ
−
i
g
τ
k
W
k
μ
W
−
i
g
6
B
μ
q
j
q
q
j
q
L
+
q
j
q
R
i
γ
μ
∂
μ
−
i
2
g
3
B
μ
q
j
q
R
+
q
j
q
R
i
γ
μ
∂
μ
+i
g
3
B
μ
q
j
q
R
=
3
j
=
1
"
g
4
q
j
q
γ
μ
(
1
−
γ
5
)
W
1
μ
W
q
j
q
+
q
j
q
γ
μ
(
1
−
γ
5
)
W
1
μ
W
q
j
q
+
g
4
i
q
j
q
γ
μ
(
1
−
γ
5
)
W
2
μ
W
q
j
q
−
i
q
j
q
γ
μ
(1
−
γ
5
)
W
2
μ
W
q
j
q
+
g
4
q
j
q
γ
μ
(1
−
γ
5
)
W
3
μ
W
q
j
q
−
q
j
q
γ
μ
(1
−
γ
5
)
W
3
μ
W
q
j
q
+
i
2
q
j
q
γ
μ
(
1
−
γ
5
)
∂
μ
−
i
g
6
B
μ
q
j
q
+
i
2
q
j
q
γ
μ
(
1
−
γ
5
)
∂
μ
−
i
g
6
B
μ
q
j
q
+
i
2
q
j
q
γ
μ
(
1
+
γ
5
)
∂
μ
−
i
2
g
3
B
μ
q
j
q
+
i
2
q
j
q
γ
μ
(
1
+
γ
5
)
∂
μ
+i
g
3
B
μ
q
j
q
)
,
(
3.55
)

84 3 Neutrinos beyond the
S
tandard Mode
l
whe
r
e
q
j
q
a
n
d
q
j
q
(
for
j
=1
,
2
,
3
)
run over
(
u
,c,
t
)
and
(
d
,s,
b
)
, respectively.
The trans
f
ormation properties o
fg
au
g
e
fi
elds
B
μ
a
n
d
W
i
μ
W
u
nder
C
and P
h
ave been given in Eq.
(
3.48
)
. With the help of Table 3.5, one can see that
the relevant spinor bilinears transform under C and P as follows:
ψ
1
γ
μ
(
1
±
γ
5
)
ψ
2
C
−→ −
ψ
2
γ
μ
(
1
∓
γ
5
)
ψ
1
,
ψ
1
γ
μ
(
1
±
γ
5
)
ψ
2
P
−→
+
ψ
1
γ
μ
(1
∓
γ
5
)
ψ
2
,
ψ
1
γ
μ
(
1
±
γ
5
)
ψ
2
C
P
−→ −
ψ
2
γ
μ
(1
±
γ
5
)
ψ
1
,
(
3.56
)
w
i
th
x
→
−
x
u
nder P and
C
P
f
o
r
ψ
1
a
n
d
ψ
2
.
Furt
h
ermore
,
ψ
1
γ
μ
(1
±
γ
5
)
∂
μ
ψ
2
C
−→
ψ
2
γ
μ
(
1
∓
γ
5
)
∂
μ
ψ
1
,
ψ
1
γ
μ
(1
±
γ
5
)
∂
μ
ψ
2
P
−→
ψ
1
γ
μ
(1
∓
γ
5
)
∂
μ
ψ
2
,
ψ
1
γ
μ
(1
±
γ
5
)
∂
μ
ψ
2
C
P
−→
ψ
2
γ
μ
(1
±
γ
5
)
∂
μ
ψ
1
,
(
3.57
)
w
i
th
x
→−
x
under P and
C
P
f
or
ψ
1
a
n
d
ψ
2
.
Then it is strai
g
ht
f
orward
to check that
L
q
i
nEq.
(
3.55
)
is formally invariant under CP. Following the
s
ame procedure and using Eqs.
(
3.48
)
,
(
3.56
)
and
(
3.57
)
, one can easily show
that
L
l
=
L
i
/
D
//
L
+
E
R
i
/
∂
//
E
R
i
salso
C
P-invariant. Thus we conclude that
L
F
i
s invariant under CP
.
Th
e
l
ast step is to examine w
h
et
h
e
r
L
Y
i
s CP-conserving or not. Explicitly
,
−
L
Y
=
Q
L
Y
u
YY
˜
HU
R
UU
+
Q
L
Y
d
YY
HD
R
+
L
Y
l
YY
HE
R
+h
.
c
.
=
3
j,
k
=
1
(
Y
u
YY
)
j
k
q
j
q
q
j
q
L
φ
0
∗
−
φ
−
q
k
R
+
(
Y
d
Y
Y
)
j
k
q
j
q
q
j
q
L
φ
+
φ
0
q
k
R
+(
Y
l
YY
)
jk
ν
j
ν
l
j
L
φ
+
φ
0
l
k
R
+
h
.
c
.
=
3
j
,
k
=
1
*
(
Y
u
YY
)
j
k
2
q
j
q
(
1+
γ
5
)
q
k
φ
0
∗
−
q
j
q
(
1
+
γ
5
)
q
k
φ
−
+
(
Y
u
YY
)
∗
j
k
2
q
k
(
1
−
γ
5
)
q
j
q
φ
0
−
q
k
(1
−
γ
5
)
q
j
q
φ
+
+
(
Y
d
YY
)
jk
2
q
j
q
(
1+
γ
5
)
q
k
φ
+
+
q
j
q
(
1+γ
5
)
q
k
φ
0
+
(
Y
d
YY
)
∗
jk
2
q
k
(1
−
γ
5
)
q
j
q
φ
−
+
q
k
(
1
−
γ
5
)
q
j
q
φ
0
∗
+
(
Y
l
YY
)
j
k
2
ν
j
ν
(
1
+
γ
5
)
l
k
φ
+
+
l
j
(
1+
γ
5
)
l
k
φ
0
+
(
Y
l
YY
)
∗
jk
2
l
k
(
1 −
γ
5
)
ν
j
ν
φ
−
+
l
k
(
1 −
γ
5
)
l
j
φ
0
∗
)
,
(
3.58
)

3.3
C
, P and T Properties o
f
Fermion Fields 85
whe
r
e
q
j
q
a
n
d
q
j
q
(
fo
r
j
=1
,
2
,
3
)
run over
(
u
,c,
t
)
and
(
d
,s,
b
)
, respectively
;
while
ν
j
ν
a
nd l
j
(
fo
r
j
=1
,
2
,
3)
run over
(
ν
e
,
ν
μ
,ν
τ
)
and
(
e, μ,
τ
)
, respectively.
B
ecause of
φ
±
→
φ
∓
,
φ
0
→
φ
0
∗
a
n
d
ψ
1
(
1
±
γ
5
)
ψ
2
→
ψ
2
(
1
∓
γ
5
)
ψ
1
under
C
P
a
s shown in Tables 3.4 and 3.5, we immediatel
y
arrive at
−L
Y
CP
−
→
3
j,
k
=
1
*
(
Y
u
YY
)
j
k
2
q
k
(
1 −
γ
5
)
q
j
q
φ
0
−
q
k
(1
−
γ
5
)
q
j
q
φ
+
+
(
Y
u
YY
)
∗
jk
2
q
j
q
(
1+
γ
5
)
q
k
φ
0
∗
−
q
j
q
(
1
+
γ
5
)
q
k
φ
−
+
(
Y
d
YY
)
j
k
2
q
k
(1
−
γ
5
)
q
j
q
φ
−
+
q
k
(1
−
γ
5
)
q
j
q
φ
0
∗
+
(
Y
d
YY
)
∗
j
k
2
q
j
q
(
1+
γ
5
)
q
k
φ
+
+
q
j
q
(
1
+
γ
5
)
q
k
φ
0
+
(
Y
l
YY
)
jk
2
l
k
(
1
−
γ
5
)
ν
j
ν
φ
−
+
l
k
(
1
−
γ
5
)
l
j
φ
0
∗
+
(
Y
l
Y
Y
)
∗
j
k
2
ν
j
ν
(
1
+
γ
5
)
l
k
φ
+
+
l
j
(
1
+
γ
5
)
l
k
φ
0
)
,
(
3.59
)
w
i
th
x
→
−
x
f
or both scalar and spinor
fi
elds under consideration.
C
ompar-
i
ng between Eqs.
(
3.58
)
and
(
3.59
)
, we see that
L
Y
w
ill be formall
y
invarian
t
u
nder
C
P if the conditions
(
Y
u
YY
)
j
k
=(
Y
u
YY
)
∗
jk
,
(
Y
d
YY
)
jk
=
(
Y
d
YY
)
∗
j
k
,
(
Y
l
YY
)
jk
=
(
Y
l
YY
)
∗
jk
(
3.60
)
a
re satis
fi
ed. In other words, the Yukawa couplin
g
matrices
Y
u
Y
Y
,
Y
d
YY
a
n
d
Y
l
YY
m
ust be real to guarantee the CP invariance of
L
Y
. Given three massles
s
n
eutrinos in the SM, it is always possible to mak
e
Y
l
YY
r
eal by redefining th
e
phases o
f
char
g
ed-lepton
fi
elds. But it is in
g
eneral impossible to make bot
h
Y
u
Y
Y
a
nd
Y
d
YY
real for three families of quarks
(
Kobayashi and Maskawa, 1973
),
a
nd thus
C
P violation can only appear in the quark sector
.
G
iven massive neutrinos be
y
ond the
S
M
,
L
Y
must be
m
od
i
fied
.Th
es
im
-
plest way is to introduce three right-handed neutrinos and incorporate the
D
irac neutrino mass term in Eq.
(
3.10
)
into
L
Y
.In
th
i
scaseo
n
e should also
a
dd the kinetic term o
f
three ri
g
ht-handed neutrinos into
L
F
.Itisstrai
g
ht-
f
orward to show that the conditions of CP invariance in the lepton sector
tu
rn
out to be
Y
ν
Y
Y
=
Y
∗
ν
Y
Y
,Y
l
YY
=
Y
∗
l
YY
,
(
3.61
)
exactl
y
in parallel with the quark sector. I
f
an e
ff
ective Ma
j
orana mass ter
m
i
s introduced int
o
L
Y
,
as shown in Eq.
(
3.18
)
, then the conditions of C
P
i
nvariance in t
h
e
l
epton sector
b
ecome
M
L
MM
=
M
∗
L
MM
,Y
l
YY
=
Y
∗
l
YY
,
(
3.62
)
w
h
e
r
e
M
L
MM
is the e
ff
ective Majorana neutrino mass matrix.
O
ne may dia
g
-
onalize bot
h
Y
ν
Y
Y
(
or
M
L
M
M
)
and
Y
l
Y
Y
to make them real and
p
ositive, but such
