Xing Zh., Zhou Sh. Neutrinos in Particle Physics, Astronomy and Cosmology
Подождите немного. Документ загружается.


21
66
Neutrinos
f
rom
S
tar
s
Table 6.1 Fundamental physical constants in the SI units, where the figures in the
p
arentheses a
f
ter the values denote the
1
σ
u
ncertainties in the last digits
(
Moh
r
et
al.
,
2007
,
2008
;
Nakamur
a
et a
l.
, 2010
)
Q
uantity
S
ymbol Valu
e
s
peed o
f
li
g
ht in vacuu
m
c
2
.
99 792
4
58
×
1
0
8
ms
−
1
P
l
a
n
c
k
co
n
sta
n
t
h
6
.
626 068 96
(
33
)
×
1
0
−
34
Js
r
educed
Pl
a
n
c
k
co
n
sta
n
t
1
.
054 571 628
(
53
)
×
1
0
−
3
4
J
s
B
o
l
t
zm
a
nn
co
n
sta
n
t
k
B
1
.
380 6504
(
24
)
×
1
0
−
23
J
K
−
1
Newto
n
co
n
sta
n
t
G
N
6
.
674 28
(
67
)
×
10
−
1
1
m
3
kg
−
1
s
−
2
S
te
f
an-Boltzmann constan
t
σ
S
B
5
.
670 400
(
40
)
×
1
0
−
8
W
m
−
2
K
−
4
Wien constan
t
b
2
.
897 7685
(
51
)
×
1
0
−
3
mK
A
vo
g
adro constant
N
A
N
6
.
022 141 79
(
30
)
×
1
0
−
2
3
m
o
l
−
1
electron charge magnitud
e
e
1
.
602 176 487
(
40
)
×
10
−
1
9
C
electron mass m
e
9
.
1
09 382 15
(
45
)
×
1
0
−
3
1
kg
pro
t
on mass m
p
1
.
672 621 637
(
83
)
×
10
−
27
kg
n
eu
t
ron mas
s
m
n
1
.
674 927 211
(
84
)
×
10
−
27
kg
a
tomicmassunit m
H
1
.
660 538 782
(
83
)
×
10
−
27
kg
Table 6.2 Conversion factors from the SI units to the cgs units, or vice versa
(
Carroll and Ostlie, 2007. With permission from Pearson Education, Inc.
)
Q
uantity
S
I unit c
g
s unit
C
onversion
f
acto
r
l
ength m cm 10
−
2
m
ass kg g 10
−
3
time s s 1
c
harge C esu
3
.
335 6
4
095
2
×
1
0
−
1
0
f
orce N
(
kg m
s
−
2
)
dyne
(
gcm
s
−
2
)
1
0
−
5
energy J
(
Nm
)
erg
(
dyne cm
)
10
−
7
power W
(
Js
−
1
)
erg
s
−
1
1
0
−
7
pressure Pa
(
Nm
−
2
)
dyne c
m
−
2
10
−
1
radius R,onema
y
define the effective temperatur
e
T
eff
TT
vi
a
L
=
4
π
R
2
σ
SB
T
4
eff
TT
,
i
mplying that the surface flux is given by
F
=
L
/
(4
π
R
2
)=
σ
SB
T
4
eff
TT
.Ta
k
ing
the
S
un
f
or exam
p
le, we can estimate the tem
p
erature at its sur
f
ace:
T
TT
=
L
4
π
σ
SB
R
2
1
/
4
≈
5777 K
.
(
6.6
)
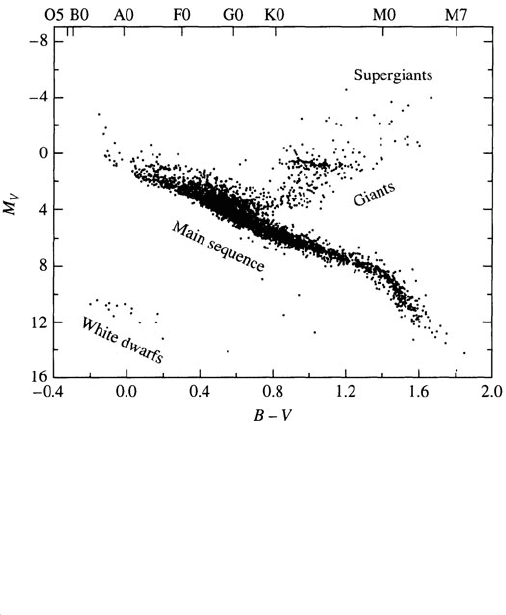
6
.1
S
tellar Evolution in a Nutshell 21
7
Fi
g
. 6.1 The color-ma
g
nitude dia
g
ram for the stars from the Hipparchos catalo
g
,
where the spectral types are given at the top border
(
Carroll and Ostlie, 2007. With
permission from Pearson Education, Inc.
)
This result means that the spectrum o
f
sunli
g
ht is peaked a
t
λ
m
ax
≈
502
nm.
The color-magnitude diagram can also be represented as a relationship be
-
tween
T
eff
TT
a
n
d
L
. The stars havin
g
the same luminosity may appear di
ff
erent
c
olors because o
f
their di
ff
erent radii. Furthermore, the initial masses o
f
stars
a
re crucial for their later evolution and account for the distinct branches in
F
i
g
. 6.1. A successful theory of stellar evolution should predict the correlatio
n
a
mon
g
the mass, luminosity and radius o
f
astar
.
A common method to exactly measure the masses of stars has bee
n
l
ackin
g
.Themasso
f
the
S
un can be determined
f
rom Kepler’s third law,
P
2
=
4
π
2
d
3
/
(
G
N
M
)
,wher
e
P
a
nd
d
stand respectivel
y
for the period of a
planet and its average distance from the Sun. Note that a planet’s mass is
n
e
gl
i
g
i
bl
eascompare
d
wit
h
t
h
eso
l
ar mass. Ta
k
in
g
t
h
ep
l
anet as t
h
e Eart
h,
one can derive the solar mass by inputtin
g
the relevant properties of the Earth
a
n
d
t
h
e precise
l
y-measure
d
Newton constan
t
G
N
. Another case, in which th
e
s
te
ll
ar mass can
b
e
d
etermine
d
,ist
h
at t
h
estar
h
appens to
b
ea
b
inar
y
star
.
Given the distance
d
of a binar
y
star and its orbital plane perpendicular t
o
the line of sight of an observer, one may figure out the mass ratio of th
e
pr
i
mar
y
star to
i
ts compan
i
on star:
M
1
/
M
2
=
θ
2
/θ
1
,w
h
ere
θ
1
a
n
d
θ
2
a
r
e
the angles spanned by the corresponding semimajor axes
a
1
a
nd
a
2
.Onth
e
other hand, the total mass o
f
a binary star can be extracted by usin
g
Kepler’
s
third law. The realistic situation ma
y
o
f
course be complicated b
y
the motio
n
of the center of mass of a binary star
(
Carroll and Ostlie, 2007
).

21
86
Neutrinos
f
rom
S
tar
s
6.1.2 Basic Equations of Stellar Evolutio
n
A
star and its d
y
namics can well be understood in some reasonable approxi
-
m
ations. In fact, the spherical symmetry is quite a good approximation du
e
to the isotropic sel
f
-
g
ravity o
f
the system. It is also reasonable to assume hy
-
d
rodynamic and thermal equilibrium, at least for the main-sequence stars. I
n
order to make clear these points, we estimate the timescales o
f
some impor-
tant processes in stars. First, the typical velocity o
f
a mass point in the
g
ravit
y
of a star with mass
M
a
nd radius
R
i
s the escape velocity
v
=
G
N
M
/
R.
The dynamical timescale is de
fi
ned as the time durin
g
which the mass poin
t
c
an travel from the surface to the center of a star at the s
p
ee
d
v
,
τ
dyn
ττ
≈
R
v
=
!
R
3
G
N
M
≈
1
0
3
!
R
R
3
M
M
s
.
(
6.7
)
Note that
τ
dyn
τ
≈
10
3
s
is much shorter than the age of the Sun, which is
ab
out
1
.
5
×
10
17
s. T
h
is o
b
servation imp
l
ies t
h
at t
h
estarwi
ll
co
ll
apse in
s
uch a short time, i
f
there is no pressure
f
orce to balance the
g
ravity. I
f
the pressure exceeds the gravity, however, the dynamical process may b
e
a
vio
l
ent exp
l
osion. In t
h
is sense a sta
bl
estars
h
ou
ld b
e assume
d
to
b
ei
n
the hydrostatic equilibrium state. Second, we introduce the gravitational
(
or
K
elvin-Helmholtz
)
timescal
e
τ
gra
ττ
.
The total gravitational potential energy is
U
∼
G
N
M
2
/R
, so the time for a star to radiate all this energy is given b
y
τ
gra
ττ
≈
U
L
=
G
N
M
2
R
L
≈
10
15
M
M
2
R
R
L
L
s
,
(
6.8
)
whe
r
e
L
i
s the stellar luminosit
y
. This timescale is shorter than one percent o
f
the age of the Sun, implying that the Sun would have burnt out if it were onl
y
powere
db
yt
h
e gravitationa
l
potentia
l
energy. Fina
ll
y, t
h
enuc
l
ear timesca
l
e
i
s set by the total mass o
f
a star and the released ener
g
y
f
rom its nuclea
r
reactions. The ratio of nuclear binding energies to the rest mass of nucleons
is about
ε
≈
10
−
3
,sot
h
e tota
l
nuc
l
ear ener
g
yisc
h
aracterize
dby
ε
M
.
T
he
n
uclear timescale is there
f
ore
g
iven as
τ
nuc
τ
τ
≈
ε
M
L
≈
5
×
10
17
M
M
L
L
s
,
(
6.9
)
which is several times lon
g
er than the a
g
eo
f
the
S
un and exceeds that o
f
th
e
U
niverse. Hence onl
y
the initial composition in a fraction rather than all o
f
t
h
este
ll
ar mass
h
as
b
een c
h
ange
db
yt
h
erma
l
nuc
l
ear reactions. T
h
ea
b
ov
e
d
iscussions indicate that the pressure,
g
ravity and nuclear reactions are th
e
m
ost important ingredients in a theory of stellar evolution. In the followin
g
we shall present a brie
f
summary o
f
the
f
undamental principles and basic
equations of stellar evolution
(
Chandrasekhar, 1938; Bahcall, 1989; Prialnik,
2
000; Salaris and Cassisi, 2005
)
.

6
.1
S
tellar Evolution in a Nutshell 21
9
(
1
)
Hyd
rostatic equi
l
i
b
riu
m
.T
h
e pressure is nee
d
e
d
to
b
a
l
ance t
h
e
g
rav
-
i
t
y
, and thus it makes the star in h
y
drostatic equilibrium. Consider a thin
s
p
h
erica
l
s
h
e
ll
at t
h
era
d
ius r. Its mass is given
b
y
Δ
M
=4
π
ρ
(
r
)
r
2
Δ
r
,
w
h
ere
ρ
(
r
)
is the local matter density and
Δ
r
de
n
otes t
h
et
hi
c
kn
ess of t
h
es
h
e
ll.
The gravity between the sphere with radius r
a
nd the mass shell reads
f
gra
ff
=
−
G
N
M
(
r
)
Δ
M
r
2
,
(
6.10
)
while the force caused by the pressur
e
P
(
r
)
is
f
p
f
f
=
4
π
r
2
[
−
P
(
r
+
Δ
r
)+
P
(
r
)].
By requirin
g
t
h
e
b
a
l
ance
f
gra
ff
+
f
p
f
f
=0an
d
settin
g
Δ
r
→
0, one o
b
tains
d
P
(
r
)
d
r
=
−
G
N
M
(
r
)
ρ
(
r
)
r
2
,
(
6.11
)
w
h
ere t
h
e tota
l
mass
M
(
r
)
contained in the sphere with radiu
s
r
is given
b
y
M
(
r
)
=
7
r
0
77
4
π
r
2
ρ
(
r
)
d
r
. The latter can also be expressed in the di
ff
erentia
l
f
orm a
s
d
M
(
r
)
d
r
=
4
π
r
2
ρ
(
r
)
, which is just the equation of mass continuity
.
Since the right-hand side of Eq.
(
6.11
)
is always negative, the pressure should
d
ecrease as the radius increases. A rou
g
h estimate of the pressure in the cente
r
oftheSunleadsusto
d
P
(
r
)
d
r
∼
P
s
PP
−
P
c
P
P
R
∼
−
P
c
PP
R
,
(
6.12
)
whe
r
e
P
s
PP
≈
0
an
d
P
c
PP
stand respectively for the pressure at the surface an
d
i
n the center of the Sun. Comparing between Eqs.
(
6.11
)
and
(
6.12
)
,wege
t
P
c
PP
∼
G
N
M
ρ
R
∼
2
.
7
×
1
0
15
d
y
ne cm
−
2
,
(
6.13
)
w
h
ere ρ
=
M
/
(
4
π
R
3
/
3)
∼
1
.
41 g c
m
−
3
i
s the average density of the
Sun.
A
more accurate calculation
y
ields
P
c
P
P
=
2
.
34
×
10
1
7
dy
ne cm
−
2
,w
h
ic
h
s
hould be com
p
ared with the standard atmos
p
heric
p
ressure 1 atm = 1
.
013
×
10
6
d
yne c
m
−
2
.
We see that the central pressure of the Sun is very high, so
a
re its temperature an
dd
ensit
y
to
b
es
h
own
b
e
l
ow
.
(
2
)
E
quation o
f
state
.
There are essentiall
y
two kinds of contributions t
o
the pressure: one is from the ideal gas consisting of electrons and ionize
d
a
toms, and the other is
f
rom radiation or photons. More importantl
y
,the
pressure may come from the degenerate electrons and neutrons such as in
the white dwarfs and neutron stars. The pressure of the ideal gas is given by
P
gas
P
P
=
nk
B
T
w
i
t
h
k
B
b
ein
g
the Boltzmann constant and
n
b
ein
g
the particle
n
umber density. One may also express this pressure a
s
P
gas
P
P
=
ρk
B
T/
(
μ
m
H
),
whe
r
e
μ
≡
m/m
H
d
enotes t
h
emeanmo
l
ecu
l
ar wei
gh
t,
m
H
is the ato
mi
c
m
ass unit, and
m
≡
ρ/
n
r
epresents the avera
g
emasso
f
a
g
as particle. Th
e
pressure of radiation is related to the energy density through
P
rad
P
P
=
u/
3
wit
h

22
06
Neutrinos
f
rom
S
tar
s
u
=
aT
4
,
w
h
er
e
a
=4
σ
SB
/
c
=7
.
56
×
10
−
15
er
g
cm
−
3
K
−
4
i
sthe
r
ad
i
at
i
o
n
c
onstant. The total
p
ressure turns out to b
e
P
=
P
gas
P
P
+
P
rad
P
P
=
ρk
T
μm
H
+
1
3
a
T
4
.
(
6.14
)
In or
d
er to
d
etermine t
h
emeanmo
l
ecu
l
ar wei
gh
t, one
h
as to
k
now t
h
ec
h
em
-
i
cal composition o
f
the
g
as. For the ionized
g
as, we hav
e
1
μm
H
=
1
m
=
n
ρ
=
j
N
j
N
(
1+
z
j
z
)
j
N
j
N
m
j
,
(
6.15
)
whe
r
e
N
j
N
i
st
h
e
n
u
m
be
r
of t
h
e“
j
”
atoms
,
z
j
z
de
n
otes t
h
e
n
u
m
be
r
of f
r
ee
e
l
ect
r
o
n
s
in
t
h
e“
j
”
ato
m
a
n
d
m
j
i
s its mass. We de
fi
ne the atomic number
A
j
=
m
j
/m
H
and the mass fraction
X
j
X
,
which is the ratio of the total mas
s
of t
h
e“
j
”
atoms to that of the gas. Then Eq.
(
6.15
)
can be rewritten as
1
μ
m
H
=
j
N
j
N
(
1
+
z
j
z
)
N
j
N
m
j
·
N
j
N
m
j
j
N
j
N
m
j
=
j
N
j
N
(
1
+
z
j
z
)
N
j
N
A
j
m
H
X
j
X
.
(
6.16
)
To illustrate, we assume a completely ionized gas and denote the mass frac-
tions of hydrogen, helium and other heavier elements a
s
X
,
Y
a
n
d
Z
w
i
th
X
+
Y
+
Z
=
1.
S
o the mean molecular wei
g
ht is
g
iven by
1
μ
=2
X
+
3
4
Y
+
8
1+
z
j
z
A
j
9
Z
≈
2
X
+
3
4
Y
+
1
2
Z.
(
6.17
)
N
ote that 1
+
z
j
z
≈
z
j
z
an
d
A
j
≈
2
z
j
z
hold for the elements much heavier tha
n
h
e
l
ium. For a neutra
l
gas, one may set
z
j
z
=0inEq.
(
6.16
)
and then obtain
μ
−
1
≈
X
+
Y
/
4
+
A
−
1
j
Z
.
For youn
g
stars wit
h
t
h
e typica
l
compositio
n
X
=
0
.
71
,
Y
=
0
.
27 and
Z
=
0
.
02, one may ge
t
μ
=
1
.
2
9 for a neutral gas o
r
μ
=0
.
6
1 for a completely ionized gas. Omitting the pressure of radiation, w
e
c
an estimate the temperature of the solar core by using Eq.
(
6.14
):
T
c
TT
∼
μm
H
P
c
PP
ρ
k
B
∼
1
.
4
4
×
10
7
K
,
(
6.18
)
where Eq.
(
6.13
)
an
d
μ
=
0
.
61
f
or an ionized
g
as have been used. This rou
g
h
estimateisin
g
ood a
g
reement with the result
T
c
TT
=
1
.
5
7
×
1
0
7
K
f
r
o
m
a
m
o
r
e
d
etailed analysis. In fact, the chemical composition in the Sun is slightly
d
i
ffe
r
e
n
tf
r
om
X
=
0
.
7
1
,
Y
=
0
.
27
an
d
Z
=0
.
0
2 because a
f
raction o
f
h
ydro
g
en has been converted into helium
.

6
.1
S
tellar Evolution in a Nutshell 221
(
3
)
C
hemical composition.Hy
d
ro
g
en an
dh
e
l
ium
d
ominate t
h
einitia
l
c
hemical composition of stars, but nuclear reactions takin
g
place in the stars
will change the element abundances. Consider a two-body nuclear reaction
I
(
Z
i
Z
,
A
i
)+
J
(
Z
j
Z
,
A
j
)
K
(
Z
k
,
A
k
)+
L
(
Z
l
,A
l
)
,
(
6.19
)
where
Z
m
Z
a
n
d
A
m
(
for
m
=
i
,j,k,
l
)
denote the atomic and mass number
s
of t
h
ee
l
e
m
e
n
t
I
,
J
,
K
o
r
L
.To
fig
ure out the number density
n
i
,wenee
d
to
kn
ow t
h
ec
r
oss sect
i
o
n
of t
hi
s
r
eact
i
o
n
σ
i
jk
and the relative velocit
y
v
betwee
n
I
a
nd
J
.
Because o
f
Z
i
Z
+
Z
j
Z
=
Z
k
+
Z
l
an
d
A
i
+
A
j
=
A
k
+
A
l
,
th
e
i
n
de
x“
l
”
can
b
e omitte
d
in
d
enotin
g
σ
i
j
k
.Thee
ff
ective tar
g
et area is
n
i
σ
i
j
k
,
a
n
dt
h
e
n
u
m
be
r
of t
h
e“
J
” particles crossin
g
this area in unit time i
s
n
j
v
.
So the number of reactions occurring in unit time and unit volume is given
by
n
i
n
j
σ
i
j
k
v
or
n
i
n
j
R
i
j
k
w
i
th
R
i
j
k
=
σ
i
j
k
v
b
ein
g
the interaction rate.
A
s
a
result
,
the evolution of
n
i
r
eads
˙
n
i
=
−
n
i
j,
k
n
j
R
ijk
+
k
,
l
n
k
n
l
1+
δ
kl
R
kl
i
,
(
6.20
)
where the factor
1
/
(
1
+
δ
kl
)
takes account of the identical particles wit
h
k
=
l
.
Fo
r
the
ini
t
i
al states w
i
th
i
=
j
, the factor
1
/
2
w
i
ll be ca
n
celled because the
r
eact
i
o
nr
educes t
h
e
n
u
m
be
r
of t
h
e
“
I
”
particles b
y
two units. In terms o
f
themassfraction
X
j
X
of the
“
J
”
particles, Eq.
(
6.20
)
can be recast into
˙
X
i
A
i
=
ρ
m
H
⎡
⎣
−
X
i
A
i
j
,
k
X
j
X
A
j
R
i
j
k
+
k
,
l
X
k
X
l
A
k
A
l
·
R
kli
1+
δ
kl
⎤
⎦
,
(
6.21
)
w
h
ere
R
ijk
r
e
l
ies on t
h
e matter
d
ensity, temperature an
d
c
h
emica
l
e
l
ements
.
(
4
)
E
ner
gy
conservation. For a sp
h
erica
l
s
h
e
ll
at t
h
era
d
iu
s
r
w
i
th a th
i
ck-
n
ess
d
r
, its local or interior luminosit
y
is defined as
d
L
r
=4
π
r
2
ρ
(
r
)
d
r
wit
h
being the coefficient of energy generation per unit time and unit mass. The
ener
g
y conservat
i
on means
d
L
r
d
r
=4
π
r
2
ρ
(
r
)
,
(
6.22
)
where
=
g
ra
+
nu
c
−
ν
i
ncluding the gravitational potential energy, the
energy released from nuclear reactions and that carried away by neutrinos.
(
5
)
E
ner
gy
trans
f
e
r
.
There are three di
ff
erent ways o
f
ener
g
y transport in
s
tars: radiation, convection and conduction. Radiation means that energie
s
pro
d
uce
db
yt
h
e gravitationa
l
potentia
l
an
d
nuc
l
ear reactions are carrie
d
a
way by photons from the core to the surface of a star.
A
lthou
g
h convectio
n
i
sim
p
ortant in the stellar evolution, thermal radiation and conduction are
d
ominant in the
S
un.
C
onvection in the
S
un is rather complicated and only
relevant in its outer la
y
er with a thickness o
f
about
0
.
3
R
(
Basu and Antia,
2
008
)
. Let us first discuss radiation. Consider a flux of photons
F
rad
F
F
traversing

222
6
Neutrinos
f
rom
S
tar
s
aslabw
i
th th
i
ck
n
ess d
r
.T
h
ep
h
otons wi
ll b
ea
b
sor
b
e
dby
matter in t
h
es
l
a
b
,
a
nd its ener
g
y loss is
g
iven by d
F
rad
F
F
=
−
κ
γ
ρF
rad
FF
d
r
,
where
κ
γ
denotes th
e
opacity coefficient an
d
ρ
i
st
h
e matter
d
ensity. Note t
h
a
t
κ
γ
itself depends o
n
the matter densit
y
, chemical composition, and temperature o
f
the slab. Th
e
radiation flux is then
g
iven b
y
F
rad
FF
=
F
0
FF
e
−
κ
γ
ρ
r
=
F
0
FF
e
−
r
/
λ
γ
,
(
6.23
)
whe
r
e
F
0
F
F
is t
h
e
ini
t
i
a
l
flu
x
a
n
d
λ
γ
≡
(
κ
γ
ρ
)
−
1
can
b
ere
g
ar
d
e
d
as t
h
emea
n
f
ree
p
ath of
p
hotons. Since
d
F
rad
FF
/
c
m
easures a chan
g
e of the momentum of
radiation which is equivalent to a change of the pressure of radiation d
P
rad
PP
,
we hav
e
d
P
rad
PP
d
r
=
−
κ
γ
ρF
rad
FF
/
c.
G
iven
P
rad
PP
=
aT
4
/
3
, the local luminosity
L
r
=
4
π
r
2
F
rad
FF
can be related to the temperature gradient as follows
:
L
r
=
−
4
π
r
2
4
ac
T
3
3
κ
γ
ρ
·
d
T
d
r
.
(
6.24
)
We procee
d
to
d
iscuss con
d
uction, t
h
e energy transporte
db
yt
h
e partic
l
es
except photons. The ener
g
y
fl
ux o
f
non-de
g
enerate electrons can be writte
n
as
F
e
F
F
=
n
e
E
e
v
,
wher
e
n
e
denotes the average number density of electrons,
E
e
=
3
k
B
T
/
2ist
h
et
h
erma
l
energy, an
d
v
i
s the average velocity of electrons.
N
ote that the absorption o
f
electrons leads to a decrease o
f
the ener
g
y
fl
ux
:
d
F
e
FF
=
−
λ
−
1
e
F
e
FF
d
r
w
ith
λ
e
being the mean free path of electrons. Therefore,
F
e
FF
=
−
3
2
λ
e
n
e
k
B
v
d
T
d
r
.
(
6.25
)
This result has a form similar to that of
F
rad
FF
=
L
r
/
(
4
π
r
2
)
as one can see
f
rom Eq.
(
6.24
)
. Combining the radiation and conduction contributions, w
e
d
e
fi
ne the total ener
g
y
fl
ux a
s
F
≡
F
rad
FF
+
F
e
FF
a
n
d
rewrite t
h
e
l
oca
ll
uminosit
y
as
L
r
=4
π
r
2
F
.
Then the overall energy transport can be expressed as
L
r
=
−
4
π
r
2
4ac
T
3
3
κρ
·
dT
d
r
,
(
6.26
)
whe
r
e
κ
−
1
≡
κ
−
1
γ
+
κ
−
1
e
is de
fi
ned, and
κ
e
=
8
acT
3
/
(9
λ
e
n
e
k
B
vρ
)
is the opac-
i
t
y
coefficient of electrons. Finall
y
, we mention that convection as a mecha
-
n
ism of the energy and chemical element transport is involved in the large
-
s
cale motion of matter in stars
(
Salaris and Cassisi, 2005
)
. Since there is n
o
s
atisfactor
y
theor
y
of convection at present, the convective flux is usuall
y
c
alculated in some approximations
(
Biermann, 1951; Vitense, 1953; B¨ohm
-
Vitense, 1958
)
. It is expected that the convective transport is insignificant i
n
the stellar core where neutrinos are produced
(
Bahcall, 1989
)
.
I
n summary, t
h
e
l
oca
ll
uminosity
L
r
(
r
)
, pressur
e
P
(
r
)
,temperatur
e
T
(
r
),
d
ensit
y
ρ
(
r
)
and chemical elements
X
i
(
fo
r
i
=1
,
2
,
···
,n
)
of a star ar
e
governed by a set of differential equations. Because of the equation of state
,

6
.1
S
tellar Evolution in a Nutshell 22
3
we a
r
e
l
eft w
i
t
h
n
+ 3 independent quantities
(
i.e.
,
P
,
T
,
L
r
a
n
d
X
i
)
whic
h
a
re described by the followin
g
n
+
3 differential e
q
uations
:
d
P
(
r
)
d
r
=
−
G
N
M
(
r
)
ρ
(
r
)
r
2
,
d
T
(
r
)
d
r
=
−
3κρ
4
ac
T
3
(
r
)
·
L
r
(
r
)
4
π
r
2
,
d
L
r
(
r
)
d
r
=4
π
2
r
2
ρ
(
r
)
,
(
6.27
)
a
nd
d
X
i
d
t
=
f
i
ff
[
X
i
,
ρ
(
r
)
,T
(
r
)]
with
f
i
ff
b
eing definable through Eq.
(
6.21
)
.To
s
o
l
ve t
h
ese equations, one
h
as to impose t
h
einitia
l
con
d
itions an
d
ca
l
cu
l
at
e
the energy production coefficien
t
,
the opacit
y
coefficien
t
κ
a
nd the interac
-
t
i
o
nr
ates
R
i
j
k
by means o
f
particle physics.
6.1.3 Ener
g
y Sources o
f
Star
s
T
h
e
g
ravitationa
l
potentia
l
ener
g
yan
d
t
h
erma
l
nuc
l
ear reactions are two
i
mportant ener
g
y sources o
f
stars. First, let us present the virial theore
m
a
nd apply it to the stars in hydrostatic equilibrium. With the help of d
M
=
4
π
ρr
2
d
r
,onemayrewriteEq.
(
6.11
)
as
d
P
d
M
=
−
G
N
M
/
(
4
π
r
4
)
.The
n
M
s
0
4
π
r
3
d
P
d
M
d
M
=
−
M
s
0
G
N
M
r
d
M
,
(
6.28
)
where
M
s
i
s the total mass of the star. The right-hand side of Eq.
(
6.28
)
represents t
h
e gravitationa
l
potentia
l
energy Ω
,
w
h
i
l
eanintegration
b
y part
s
o
ni
ts
l
eft
-h
a
n
ds
i
de
l
eads to
M
s
0
12
π
r
2
P
d
r
dM
d
M
=3
M
s
0
P
ρ
d
M
,
(
6.29
)
w
h
ere we
h
ave use
d
P
=
P
s
PP
=
0
at the surface and the mass conservatio
n
d
r
d
M
=
1
/
(
4
π
r
2
ρ
)
. For an ideal gas, the internal energy per unit mass is
u
=3
k
B
T
/
(
2
μm
H
)
and the equation of state read
s
P/ρ
=
k
B
T
/
(
μm
H
)
.So
E
qs.
(
6.28
)
and
(
6.29
)
establish a relationship between the internal energ
y
U
a
nd the gravitational potential energ
y
Ω
:
U
≡
M
s
0
u
d
M
=
−
Ω
2
,
(
6.30
)
k
nown as t
h
e viria
l
t
h
eorem. T
h
e tota
l
ener
g
yi
s
E
=
U
+
Ω
=
Ω
/
2
<
0
,as
i
t should be
f
or a bound s
y
stem.
C
onsider a star without nuclear reaction
s
but radiating energies from its surface. Its luminosity is
L
=
−
d
E
d
t
.T
he

224
6
Neutrinos
f
rom
S
tar
s
virial theorem yield
s
L
∝−
d
Ω
d
t
, implying that the gravitational potentia
l
ener
g
y decreases so as to
g
ive a positive luminosity. Hence the star has to
c
ontract when it radiates energies, and it has a negative specific heat. Th
e
viria
l
t
h
eorem can a
l
so
b
euse
d
to estimate t
h
eavera
g
e temperature. Ta
k
in
g
a
ccount of Ω
∝
−G
N
M
2
s
/
R an
d
U
=3
k
B
T M
s
/
(
2μ
m
H
)
,onemaygetth
e
a
vera
g
e temperature
T
∝M
s
/R
∝M
2
/
3
s
ρ
1
/
3
,
w
h
ere t
h
eavera
g
e
d
ensity i
s
d
efined as
ρ
∝M
s
/R
3
. For two stars with the same mass
,
the one with
a
l
ar
g
er matter
d
ensity must
h
ave a
h
i
gh
er avera
g
e temperature.
Table 6.3 Conversion factors of five frequentl
y
-used units in the s
y
stem of natural
u
ni
ts w
i
t
h
=
k
B
=
c
=1
(
Raffelt, 1996, with permission from the University o
f
Chicago Press; Raffelt and Rodejohann, 1999
)
s
−
1
c
m
−
1
KeV
g
s
−
1
10
.
33
4
·
10
−
1
0
0
.
7
6
4
×
1
0
−
1
1
0
.
6
5
8
× 1
0
−
15
1
.17
3
×
10
−
48
c
m
−
1
2
.
9
9
8
×
10
1
0
1
0
.
2289 1
.
973
×
1
0
−
5
0
.352
×
10
−
37
K1
.
3
10
×
10
1
1
4
.
369 1 0
.
862
×
1
0
−
4
1
.
5
3
7
×
10
−
37
e
V
1
.
5
1
9
×
10
1
5
0
.507
×
1
0
5
1
.
1
60
×
1
0
4
11
.
7
8
3
×
10
−
33
g0.
852
×
1
0
48
2
.
8
4
3
× 1
0
37
0
.
65
1
×
10
37
0
.
56
1 × 1
0
33
1
S
econd, let us calculate the energy production from nuclear reactions. If
a
sum o
f
the masses o
f
initial nuclei is lar
g
er than that o
ffi
nal nuclei in a
s
pecific reaction
(
i.e.
,
M
initial
MM
>M
final
M
M
)
, the energy released from this reaction
i
st
h
en
g
iven
by
Δ
E
=
M
initial
MM
−
M
final
MM
.S
uch a mass di
ff
erence comes
f
rom
the bindin
g
ener
g
yo
f
a nucleus.
G
iven a nucleus
X
(
Z
,
A
)
with mas
s
M
X
M
,
f
or example, its binding energy i
s
E
b
in
d
=
Zm
p
+(
A
−
Z
)
m
n
−
M
X
M
wit
h
m
p
=
938
.
2
7
2Me
V
an
d
m
n
= 939
.
565 MeV
b
ein
g
t
h
eprotonan
d
neutron
masses
2
.Th
e
n
uc
l
eus of
56
Fe possesses the maximal bindin
g
ener
g
yper
n
ucleon:
(
E
B
/
A
)(
56
Fe
)
=8.
7
9 MeV. That is why the elements lighter
(
o
r
h
eavier
)
tha
n
56
F
e can produce energies via thermonuclear fusion
(
or nuclear
fission
)
. Consider the energy release from the nuclear reaction in Eq.
(
6.19
)
:
Q
ij
k
=
M
I
M
+
M
J
M
−
M
K
M
−
M
L
M
.
(
6.31
)
A
s discussed in Section 6.1.2, the number of reactions occurrin
g
in unit tim
e
a
n
d
unit vo
l
ume i
s
n
i
n
j
R
ijk
wit
h
R
ijk
=
σ
i
j
k
v
b
eing t
h
e reaction rate. Wit
h
thehelpofEq.
(
6.21
)
, the rate of energy production in unit mass is given a
s
2
T
he natural units with
=
c
=
k
B
=
1 are commonly adopted in particle
physics. In this case the units of length, mass, time and temperature can be ex-
pressed in the unit of energy
(
1eV=
1
.
602
×
10
−
19
J
=1
.
602
×
10
−
12
e
rg
)
.Th
e
conversion factors of these units are listed in Table 6.3.

6
.1
S
tellar Evolution in a Nutshell 22
5
nuc
=
ρ
m
2
H
i
,j,
k
1
1
+
δ
i
j
·
X
i
X
j
X
A
i
A
j
R
i
j
k
Q
i
j
k
.
(
6.32
)
N
ote that the initial nuclei have to overcome the
C
oulomb repulsive
f
orc
e
between them, in order for the nuclear reactions to take
p
lace. The ther
-
m
al energies of the nuclei are around ke
V
∼
10
7
K,
b
ut t
h
e
b
arrier at
n
uclear distances is as hi
g
h as several MeV. Nevertheless, these reaction
s
c
an still happen via quantum tunneling effects. George Gamow pointed out
t
h
at t
h
e penetration pro
b
a
b
i
l
ity or t
h
e cross section must
b
e proportiona
l
to
exp
[
−
2
π
Z
i
Z
Z
j
Z
e
2
/
(
v
)] (
Gamow, 1928
)
. In addition, the Maxwell-Boltzman
n
d
istribution of the velocity is proportional to exp
[
−
M
g
MM
v
2
/
(
2
k
B
T
)]
,whereth
e
reduced mass o
f
the
g
as particle is de
fi
ned as
M
g
MM
≡
M
I
M
M
J
M
/
(
M
I
M
+
M
J
M
)
.Asth
e
velocit
y
v
i
ncreases, the first ex
p
onential function increases but the secon
d
one decreases. Hence the product exp
[
−
2
π
Z
i
Z
Z
j
Z
e
2
/
(
v
)]
exp
[
−
M
g
MM
v
2
/
(2
k
B
T
)]
p
ossesses a maximum, the so-called
G
amow
p
eak. The cross section is con
-
ventionally defined as
σ
ij
k
(
E
)=
S
i
j
(
E
)
E
e
xp
(
−
2
π
η
)
,
(
6.33
)
w
h
e
r
e
η
≡
Z
i
Z
Z
j
Z
e
2
/
(
v
)
. The exponential factor exp
(
−
2
π
η
)
in Eq.
(
6.33
)
c
omes from quantum tunneling and is known as the Gamow penetration fac
-
tor. A dimensional analysis yields
σ
ij
k
(
E
)
∼
π
λ
2
de
∼
π
h
2
/p
2
∝
E
−
1
,w
h
er
e
λ
de
=
h/p
i
st
h
e
d
eBro
gl
ie wave
l
en
g
t
h
an
d
E
=
p
2
/
2
M
g
MM
has bee
n
used
.T
he
a
stroph
y
sical
f
acto
r
S
ij
(
E
)
is energy-dependent and contains the informa
-
tion of nuclear structure. In practice, one may extrapolate the experimenta
l
data on
S
ij
(
E
)
at high energies to the low-energy regime relevant to stellar
environments. Because the typical temperature in stars is in the ran
g
eo
f
(
1
∼
100
)
keV and much smaller than nuclear masses, the velocity distribu
-
tion is well described b
y
the Maxwell-Boltzmann
f
unction:
R
ijk
=
2
π
1
/
2
(
k
B
T
)
3
/
2
∞
0
E
1
/
2
e
−
E
/k
B
T
vσ
(
v
)
d
E,
(
6.34
)
w
h
ere t
h
ere
l
ative ve
l
ocit
y
v
a
n
d
t
h
e
k
inetic energy
E
satisfy
E
=
M
g
MM
v
2
/
2
.
A
combination of Eqs.
(
6.33
)
and
(
6.34
)
leads us to
(
Cox and Giuli, 1968
)
R
ijk
=
!
8
π
M
g
MM
k
B
T
S
i
j
∞
0
e
−
(
y
+
C
/
√
y
)
d
y,
(
6.35
)
w
h
e
r
e
y
≡
E
/
(
k
B
T
)
,
C
=(2
π
M
g
MM
)
1
/
2
Z
i
Z
Z
j
Z
e
2
/
[
(
k
B
T
)
1
/
2
]
,an
d
S
ij
i
s assu
m
ed
to be a constant. As a matter of fact
,
S
i
j
(
E
)
takes the value at the Gamo
w
peak if its energy dependence is non-negligible
(
Bahcall, 1989
)
.
A
stronomical observations have established that all the main-se
q
uenc
e
s
tars are predominantly composed of hydrogen. Hence the energy source of
