Xing Zh., Zhou Sh. Neutrinos in Particle Physics, Astronomy and Cosmology
Подождите немного. Документ загружается.


1
86 5 Phenomenology o
f
Neutrino
O
scillations
L
et us co
n
s
i
de
rm
uo
nn
eut
rin
os a
n
da
n
t
in
eut
rin
os f
r
om
π
+
→
μ
+
+
ν
μ
a
n
d
π
−
→
μ
−
+
ν
μ
decays, which mi
g
ht be the dominant production mechanis
m
of cosmic neutrinos at a variety of astrophysical sources. In the rest frame of
the pion, the neutrino energy has been given in Eq.
(
5.72
)
. Neglecting smal
l
n
eutrino masses, one ma
y
obtain
E
0
ν
=
(
m
2
π
−
m
2
μ
)
/
(
2
m
π
)
.Insuchdecay
m
odes the wave-packet width of the final-state particle can be estimate
d
f
rom the lifetime of the decaying particle
(
Nussinov, 1976; Kayser, 1981
).
F
or the neutrinos emitted fro
m
π
±
deca
y
s in the forward direction, we hav
e
(
Farzan and Smirnov, 2008
)
σ
π
x
=
τ
π
ττ
γ
≈
E
0
ν
E
ν
τ
π
ττ
∼
(
m
2
π
−
m
2
μ
)
2
m
π
E
ν
τ
π
ττ
,
(
5.92
)
whe
r
e
τ
π
ττ
=
2
.
6
×
10
−
8
sistheli
f
etime o
f
the pion at rest
,
E
ν
i
sthe
n
eut
rin
o
ener
g
y in the observer’s frame, an
d
γ
denotes the Lorentz boost factor for
a
transformation from the rest frame of the decaying pion to the observer’
s
f
rame.
O
ne ma
yf
ollow a similar wa
y
to estimate the wave-packet width
σ
μ
x
f
or the neutrinos emitted from
μ
±
d
eca
y
s
:
μ
+
→
e
+
+
ν
μ
+
ν
e
an
d
μ
−
→
e
−
+
ν
μ
+
ν
e
.ComparedwiththewidthinEq.
(
5.92
),
σ
μ
x
i
sen
h
ance
db
ya
factor
τ
μ
τ
/τ
π
ττ
∼
10
2
,w
h
ere
τ
μ
τ
=
2
.
2
×
10
−
6
s
i
st
h
e
li
fet
im
eoft
h
e
m
uo
n
at
rest. The ratio of the wave-
p
acket se
p
aration to the wave-
p
acket width turns
out to be
(
Farzan and Smirnov, 2008
)
d
L
σ
π
x
=
Δ
m
2
m
π
L
(
m
2
π
−
m
2
μ
)
E
ν
τ
π
ττ
,
(
5.93
)
which can be
f
urther expressed a
s
d
L
σ
π
x
∼
0
.
1
×
Δ
m
2
8
×
1
0
−
5
eV
2
·
L
100 M
pc
·
10 TeV
E
ν
·
2
.
6
×
10
−
8
s
τ
π
ττ
.
(
5.94
)
Given the cosmic neutrinos with ener
g
ie
s
E
∼
1
0 TeV and from certai
n
a
strop
h
ysica
l
sources at t
h
e
d
istances
L
∼
100 Mpc, t
h
e quantum co
h
erenc
e
is
m
a
in
ta
in
ed because the co
n
d
i
t
i
o
n
d
L
∼
σ
π
x
h
olds as shown in Eq.
(
5.94
)
.
This is alwa
y
s the case for the neutrinos from
μ
±
d
eca
y
s, whose wave-packet
wi
d
t
h
σ
μ
x
i
smuc
hl
arger t
h
an
σ
π
x
.
Although the coherence is not lost, th
e
oscillatory pattern o
f
ultrahi
g
h-ener
g
y cosmic neutrinos
f
rom a very distant
a
stroph
y
sical source must disappear. The reason is simpl
y
that the distanc
e
L
b
etween t
h
e source an
d
t
h
e
d
etector is muc
hl
onger t
h
an t
h
eneutrin
o
osci
ll
ation
l
en
g
t
h
λ
k
j
, so the probabilities o
f
neutrino oscillations have to be
a
veraged over many circles of oscillations and finally take the classical for
m
a
s given in Eq.
(
5.6
).
However,thesimplepictureo
ff
ree particle deca
y
s cannot be realized i
n
m
ost astrophysical environments. In a realistic case the pions and muons mus
t
i
nteract wit
h
t
h
eam
b
ient matter, suc
h
as p
h
otons. T
h
ewave-pac
k
et wi
d
t
h
s
a
re then determined b
y
the distance or the time between two successive colli-
s
ions. Furthermore, it is found that the magnetic fields can significantly affec
t

5
.3 Density Matrix Formu
l
ation 187
the wave-packet widths of neutrinos
(
Farzan and Smirnov, 2008
)
.Thesiz
e
of a wave packet is in principle possible to be measured by usin
g
the tim
e
i
nformation for a non-stationary beam
(
Stodolsky, 1998
)
.
5
.3 Dens
i
ty Matr
i
x Formulat
i
on
In this section we introduce an instructive and useful language, the density
m
atrix and
fl
avor polarization vector, to describe neutrino oscillations. In
p
articular, the
p
henomenon o
f
two-
fl
avor neutrino oscillations can be visu-
a
lized as the motion of a magnetic moment precessing about an external
m
a
g
netic
fi
eld. The terms o
f
neutrino masses and matter e
ff
ects correspond
to different kinds of external ma
g
netic fields in this formulation, in which the
d
ecoherence effects arising from the interactions of neutrinos with media ca
n
b
e easi
ly
incorporate
d.
Let us start with a brief review of the densit
y
matrix formalism in quan
-
tum mechanics. One may in general encounter two types of physical systems:
(
1
)
its state is perfectly known from the wave functio
n
Ψ
(
t
)
;
(
2
)
it is the
s
ubsystem of a larger one, and in principle does not have a wave functio
n
(
Landau and Lifshitz, 1977
)
. In the first case we can expand the state vector
|
Ψ
(
t
)
i
ntermso
f
a complete series o
f
ei
g
envectors o
f
the Hamiltonian
:
|
Ψ
(
t
)
=
n
C
n
CC
(
t
)
|
n
,
(
5.95
)
w
h
ere t
h
eei
g
enstates
|
n
are ortho
g
onal, and the coe
ffi
cients
C
n
CC
(
t
)
satisf
y
the normalization conditio
n
|
C
1
(
t
)
|
2
+
···
+
|
C
n
C
C
(
t
)
|
2
=
1. The ex
p
ectation
value of an operato
r
ˆ
O
reads
ˆ
O
=
Ψ
(
t
)
|
ˆ
O
|
Ψ
(
t
)
=
m
n
C
n
CC
(
t
)
C
∗
m
CC
(
t
)
m
|
ˆ
O
|
n
,
(
5.96
)
where
m
|
ˆ
O
|
n
≡
ˆ
O
mn
is the matrix element of the o
p
erator. The evolution
o
f
this system is
g
overned by the
S
chr¨odin
g
er equation
i
∂
∂t
|
Ψ
(
t
)
=
H
|
Ψ
(
t
)
.
(
5.97
)
N
ow we define the density operator as follows
:
ρ
(
t
)
≡|
Ψ
(
t
)
Ψ
(
t
)
|
=
m
n
C
n
CC
(
t
)
C
∗
m
CC
(
t
)
|
n
m
|
.
(
5.98
)
It is easy to verify that the density matri
x
ρ
i
s Hermitian, an
d
its e
l
ements
a
re
gi
ven as
ρ
nm
=
C
n
CC
(
t
)
C
∗
m
C
C
(
t
)
. Combining Eqs.
(
5.96
)
and
(
5.98
)
,weobtai
n
ˆ
O
=
m
n
ρ
nm
ˆ
O
m
n
=Tr
ρ
ˆ
O
.
(
5.99
)

1
88 5 Phenomenology o
f
Neutrino
O
scillations
F
urthermore, the evolution equation o
f
the densit
y
operator can be derived
f
rom the Schr¨odin
g
er equation
i
∂ρ
∂t
=
i
∂
∂t
|
Ψ
(
t
)
Ψ
(
t
)
|
+
|
Ψ
(
t
)
i
∂
∂
t
Ψ
(
t
)
|
=[
H
,
ρ
]
.
(
5.100
)
H
ence the density matrix description is equivalent to the wave function lan
-
g
ua
g
e
f
or a system with pure states. Two basic properties o
f
ρ
are Tr
[
ρ
]
=
1
a
nd ρ
2
=
ρ
. For an ensemble with mixed states, the probabilit
y
for it to be
i
nt
h
e state
Ψ
i
(
t
)
is
P
i
PP
a
nd the corresponding density operator is defined by
ρ
≡
i
P
i
PP
|
Ψ
i
(
t
)
Ψ
i
(
t
)
|
=
i
m
n
P
i
PP
C
i
n
CC
C
i
∗
m
CC
|
n
m
|
.
(
5.101
)
In this case the density matrix satisfies Tr
[
ρ
2
]
<
1. An a
pp
lication of th
e
d
ensity matrix
f
ormulation to neutrino oscillations will be discussed in the
two- and three-
fl
avor mixin
g
schemes, respectively.
5
.
3
.1 Two-flavor Neutrino
O
scillation
s
With the help o
f
the densit
y
matrix
f
ormulation, the phenomenon o
f
two-
flavor neutrino oscillations can be understood in a pictorial way which i
s
very analo
g
ous to the ma
g
netic moment precessin
g
in a ma
g
netic
fi
eld. Le
t
u
s
fi
rst consider the propa
g
ation o
f
a stationary neutrino beam in vacuum.
The flavor eigenstate
s
|
ν
e
a
n
d
|
ν
μ
a
re re
l
ate
d
to t
h
e mass eigenstates
|
ν
1
a
n
d
|
ν
2
via the
f
ollowin
g
unitary trans
f
ormation:
|
ν
e
|
ν
μ
=
U
|
ν
1
|
ν
2
≡
cos
θ
s
in
θ
−
sin
θ
cos
θ
|
ν
1
|
ν
2
.
(
5.102
)
S
ince two
f
ree neutrinos propa
g
ate in their mass ei
g
enstates
|
ν
i
w
i
t
h
defi
ni
te
masses
m
i
(
fo
r
i
=1
,
2)
, the evolution equation of
|
ν
i
(
t
)
c
an simpl
y
be
d
erived from Eq.
(
5.97
)
:
i
d
d
t
|
ν
1
(
t
)
|
ν
2
(
t
)
=
1
2
E
m
2
1
0
0
m
2
2
|
ν
1
(
t
)
|
ν
2
(
t
)
,
(
5.103
)
w
h
ere t
h
eexce
ll
ent approximation
E
i
≈
p
+
m
2
i
/
(2
p
)
due to
p
≈
E
m
i
h
as been taken
f
or relativistic neutrinos. Multiplyin
g
the le
f
t- and ri
g
ht-han
d
s
ides of Eq.
(
5.103
)
b
y
U
,
we obtain
i
d
d
t
|
ν
e
(
t
)
|
ν
μ
(
t
)
=
1
2
E
U
m
2
1
0
0
m
2
2
U
†
|
ν
e
(
t
)
|
ν
μ
(
t
)
.
(
5.104
)
Th
e
n
t
h
e effect
i
ve
H
a
mil
to
ni
a
nin
t
h
eflavo
r
bas
i
sca
n
be w
ri
tte
n
as
H
v
=
1
2
E
U
m
2
1
0
0
m
2
2
U
†
=
m
2
1
+
m
2
2
4
E
1
+
Δ
m
2
4
E
−
cos
2
θ
si
n
2
θ
sin 2
θ
cos
2
θ
(
5.105
)
5
.3 Density Matrix Formu
l
ation 189
w
i
th
Δ
m
2
≡
m
2
2
−
m
2
1
. Without loss o
fg
enerality, we tak
e
Δ
m
2
>
0
an
d
a
ll
o
w
θ
t
o vary in the ran
g
e0
θ
π
/
2.
Note t
h
at t
h
e term proportiona
l
to t
h
ei
d
entity matrix in
H
v
c
an a
l
ways
be omitted, because it does not affect flavor conversions.
A
fter discardin
g
this
term, we ma
y
further expan
d
H
v
in terms of the Pauli matrices:
H
v
=
ω
p
2
B
·
σ
,
(
5.106
)
whe
r
e
ω
p
≡
Δ
m
2
/
(
2
E
),
B
≡
(
sin
2
θ
,
0
,
−
cos 2
θ
)
an
d
σ
≡
(
σ
x
,σ
y
,
σ
z
)
.Given
the state vecto
r
|
Ψ
(
t
)
=
a
e
(
t
)
|
ν
e
+
a
μ
(
t
)
|
ν
μ
, the densit
y
matrix defined i
n
E
q.
(
5.98
)
turns out to b
e
ρ
=
|
a
e
|
2
a
e
a
∗
μ
a
μ
a
∗
e
|
a
μ
|
2
μμ
.
(
5.107
)
T
h
e
d
iagona
l
e
l
ement
s
|
a
e
|
2
a
n
d
|
a
μ
|
2
g
ive the probabilities for the system to
be
in
t
h
eflavo
r
states
|
ν
e
a
n
d
|
ν
μ
,
respectively. The o
ff
-dia
g
onal element
s
encode the information on
q
uantum coherence between two flavor states
.
Because an ar
b
itrary 2
×
2 Hermitian matrix can a
l
ways
b
eexpan
d
e
d
in terms
o
f
the identit
y
matrix and three Pauli matrices, we rewrite the expression o
f
ρ in Eq.
(
5.107
)
as
(
Fano, 1957
)
ρ
=
1
2
(
1+
P
·
σ
)
,
(
5.108
)
where
P
i
s the so-called flavor polarization vector. Now that the diagonal
e
l
e
m
e
n
ts of
ρ
g
ive the probabilities, the physical meanin
g
o
f
P
is the
n
t
r
a
n
s
-
p
arent:
i
t
s
z
-
com
p
onen
t
P
z
PP
i
s related to the probabilities throu
g
h
4
|
a
e
|
2
=
1
2
(
1+
P
z
PP
)
,
|
a
μ
|
2
=
1
2
(1
−
P
z
PP
)
.
(
5.109
)
P
repared with the new formulation of
H
v
i
nEq.
(
5.106
)
and ρ in Eq.
(
5.108
)
,
we recast the evolution equation in Eq.
(
5.100
)
into a more suggestive form
:
i˙
ρ
(
t
)
=
[
H
v
,
ρ
(
t
)]
=
ω
p
4
j
k
σ
j
,σ
k
B
j
P
k
P
P
(
t
)
=
i
ω
p
2
[
B
×
P
(
t
)]
·
σ
,
(
5.110
)
where the commutation relation
[
σ
j
,
σ
k
]
=2i
σ
l
(
fo
r
j
,
k
,
l
to
r
u
n
ove
r
1
,
2
,
3
c
yclically
)
has been used. Then Eqs.
(
5.108
)
and
(
5.110
)
lead us to the desired
f
orm of the evolution equation of
P
(
t
)(
Fano, 1957; Raffelt, 1996
):
d
d
t
P
(
t
)=
ω
p
B
×
P
(
t
)
.
(
5.111
)
4
W
ehavedefined
P
=
(
P
x
P
P
,P
y
P
P
,P
z
P
P
)
an
d
σ
=(
σ
x
,σ
y
,σ
z
)
.Sometimesitismor
e
convenient to denote the Pauli matrices as
(
σ
1
,σ
2
,σ
3
)
. These two notations are
equivalent and will be alternatively used in this section.
1
90 5 Phenomenology o
f
Neutrino
O
scillations
H
ence neutrino oscillations can be described b
y
the evolution o
f
the
fl
avor
polarization vector. To make the physical meanin
g
of
P
(
t
)
clearer, we assum
e
the initial state of a neutrino beam to be purely composed of electron neutri
-
n
os; name
ly
,
a
e
(
0
)
=1an
d
a
μ
(
0
)
=0.Eqs.
(
5.107
)
and
(
5.108
)
allow one to
d
etermine the initial value of the
p
olarization vector:
P
(
0
)
=
(0
,
0
,
1)
.Ifth
e
polarization vector points upward
(
downward
)
, the state is purely an electron
(
muon
)
neutrino. On the other hand, Eq.
(
5.111
)
means that the length of
P
(
t
)
keeps unchanged in the evolution; i.e.,
|
P
(
t
)
|
2
=
1. To solve Eq.
(
5.111
),
we write out the evolution equation for each component of
P
(
t
):
d
d
t
(
P
x
P
P
,P
y
P
P
,P
z
P
P
)=
ω
p
(
P
y
P
P
c
os 2θ
,
−
P
z
P
P
sin 2
θ
−
P
x
P
P
cos
2
θ, P
y
P
P
s
in
2
θ
)
.
(
5.112
)
G
iven the initial condition
s
P
(
0
)
=
(
0
,
0
,
1)
an
d
˙
P
(
0
)
=
(
0
,
−
ω
p
s
in
2
θ,
0)
,th
e
ab
ove equation can
b
eexact
l
yso
l
ve
d
. For examp
l
e, we o
b
tain
P
z
PP
(
t
)
=
1
−
2sin
2
2
θ
sin
2
ω
p
t
2
(
5.113
)
f
or th
e
z
-
component. This result, together with Eq.
(
5.109
)
, leads to the
s
urvival probability o
f
the electron neutrinos
:
P
(
ν
e
→
ν
e
)
=
|
a
e
(
t
)
|
2
=
1
−
sin
2
2
θ
s
i
n
2
ω
p
t
2
.
(
5.114
)
Taking
t
=
L
in the natural unit system, we see that Eq.
(
5.114
)
is consisten
t
with Eq.
(
5.9
)
. The evolution of the polarization vector is shown in Fig. 5.2.
A
tthebe
g
innin
g
P
i
s located alon
g
th
e
z
-
a
xi
sw
i
th
P
(
0
)
=
(
0
,
0
,
1
)
.Then
i
t rotates about the axis in the direction of B
=(
sin
2
θ,
0
,
−
cos
2
θ
)
,andit
s
a
n
g
u
l
ar ve
l
ocity is simp
l
y
ω
p
.
The projection o
f
P
(
t
)
on the
z
-axis
g
ives ris
e
to the survival probability, as indicated in Eqs.
(
5.113
)
and
(
5.114
).
S
o far we have dealt with the case o
f
Δ
m
2
>
0
an
d0
θ
π
/
4(
the
the normal neutrino mass hierarchy
)
. Note that the case of
Δ
m
2
<
0
an
d
0
θ
π
/
4(
the inverted neutrino mass hierarchy
)
is equivalent to the case of
Δ
m
2
>
0
an
d
π
/
4
θ
π
/
2. For the latter case, one may defin
e
θ
≡
π
/
2
−
θ
a
n
d
rep
l
ac
e
θ
w
i
th
π
/
2
−
θ
in the effective Hamiltonian.
A
s a consequence,
the direction of the magnetic field become
s
B =
(
sin
2
θ
,
0
,
cos 2
θ
)
which is
n
ow lying in the first quadrant of the
(
x
,
z
)
plane. The survival probabilit
y
i
nEq.
(
5.114
)
keeps unchanged, as it should be. All the above discussions are
app
licable for antineutrino-antineutrino oscillations
.
W
e proceed to include the matter effects in the density matrix formu
-
l
ation. The
S
chr¨odin
g
er-like equation
f
or neutrinos propa
g
atin
g
in ordinar
y
m
atter has been given in Section 5.1. The matter effects can be describe
d
by the e
ff
ective potential
V
=
√
2
G
F
n
e
,
w
h
ic
hl
inear
l
y contri
b
utes to t
he
effect
i
ve
H
a
mil
to
ni
a
n
H
m
i
nm
atte
r:
H
m
−H
v
=
√
2
G
F
n
e
10
00
=
G
F
n
e
√
2
1
+
G
F
n
e
√
2
10
0
−
1
.
(
5.115
)

5
.3 Density Matrix Formu
l
ation 19
1
z
y
x
B
P
(
0
)
P
(
t
)
2
θ
P
(
ν
e
→
ν
e
ν
)
Fig. 5.2 The evolution o
f
the polarization vector
P
(
t
)
in the flavor space, wher
e
P
(
0
)
=
(
0
,
0
,
1)
is the initial condition and the magnetic field is in the direction o
f
B
=(sin2θ,
0
,
−
c
os 2θ)wit
h
θ
being the neutrino mixing angle in vacuu
m
The first term on the right-hand side of Eq.
(
5.115
)
can be omitted becaus
e
it
i
s
irr
e
l
eva
n
tto
n
eut
rin
oflavo
r
co
n
ve
r
s
i
o
n
s
.Th
e
n
we
r
ew
ri
te t
h
eabove
e
q
uation in terms o
f
the Pauli matrices a
s
H
m
−H
v
=
λ
2
L
·
σ
,
(
5.116
)
where
λ
≡
√
2
G
F
n
e
,
and
L
=
(
0
,
0
,
1)
is the unit vector along the positive
z
-
a
xis. In a way similar to the derivation of Eq.
(
5.111
)
, the evolution equation
o
f
the polarization vector in matter is
f
ound to b
e
d
d
t
P
(
t
)
=
ω
p
B
+
λ
L
×
P
(
t
)
.
(
5.117
)
We see that matter effects are equivalent to a new magnetic field in th
e
d
ir
ect
i
o
n
of t
h
e
z
-axis. I
f
the matter densit
y
is a constant, the behavior o
f
n
eutrino flavor conversions turns out to be ver
y
similar to that in vacuum.
In this case the matter-corrected neutrino mixing angle and frequency ar
e
de
n
oted as
θ
m
a
n
d
ω
m
p
,
respective
ly
.T
h
e
y
are re
l
ate
d
to t
h
eir counterparts
i
n vacuum through ω
p
B
+
λ
L
≡
ω
m
p
B
m
w
ith B
m
≡
(
sin
2
θ
m
,
0
,
−
c
os 2
θ
m
)
.
A
s
traightforward calculation yield
s
ω
m
p
=
ω
2
p
+
λ
2
−
2
λ
ω
p
cos 2θ
,
tan 2θ
m
=
ω
p
s
in
2
θ
ω
p
cos 2
θ
−
λ
.
(
5.118
)
Note t
h
at
ω
m
p
ca
n
be defi
n
ed as
ω
m
p
≡
Δ
˜
m
2
/
(2
E
)
with
Δ
˜
m
2
bein
g
the e
ff
ec-
tive neutrino mass-squared difference in matter. Note also that Eq.
(
5.117
)
ca
n
be
r
ew
ri
tte
n
as
˙
P
(
t
)=
ω
m
p
B
m
×
P
(
t
)
. If the matter density is extremel
y
s
mall
(
i.e.,
λ
→
0
)
, one may easily reproduce neutrino oscillations in vac
-
u
um from Eqs.
(
5.117
)
and
(
5.118
)
.Inth
e
λ
→
+
∞
l
imit we can obtai
n
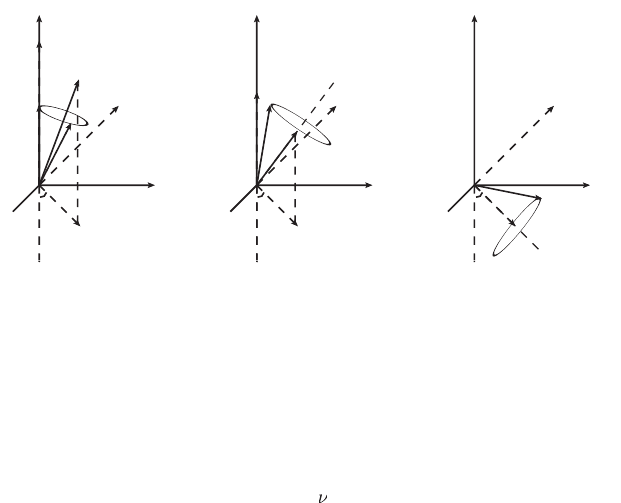
1
92 5 Phenomenology o
f
Neutrino
O
scillations
z
y
x
P
(
0
)
ω
p
ω
B
P
(
t
)
λ
L
ω
m
p
ω
B
m
ω
p
ω
B
2
θ
2
θ
ω
p
ω
B
x
y
ω
m
p
ω
B
m
y
z
λ
L
z
2
θ
(
a
)
(
c
)
(b)
x
Fig. 5.3 The visualization of two-flavor neutrino oscillations in matter:
(
a
)
at
t
h
e
b
e
g
innin
g
t
h
e matter
d
ensity is very
l
ar
g
ean
d
P
(
0
)
=
(
0
,
0
,
1)
holds, s
o
the polarization vecto
r
P
(
t
)
rotates around the effective magnetic field
B
m
=
(
sin 2
θ
m
,
0
,
−
cos 2
θ
m
)
;
(
b
)
as the matter density decreases
,
P
(
t
)
turns to rotat
e
around the new magnetic field
B
m
;
(
c
)
after the matter density approaches zero
,
B
m
a
pproache
s
B
a
n
d
P
(
t
)
rotates aroun
d
B
but spins down
tan 2
θ
m
→
0
−
,
or equivalently
θ
m
→
π
/
2, from Eq.
(
5.118
)
. This limit im
-
plies that the heavier mass eigenstate ˜
ν
2
do
min
ates
in
t
h
ee
l
ect
r
o
n
flavor
state
ν
e
.In
t
h
ecos
2
θ
> 0 case, which corres
p
onds to the normal neutrin
o
m
ass hierarchy, one has
θ
m
=
π
/
4
if the resonant condition
λ
=
ω
p
c
os
2
θ
is
sat
i
sfied
.In
t
h
e cos 2
θ<
0 case, w
h
ic
h
is equiva
l
ent to t
h
einverte
d
neutrino
m
ass hierarch
y
, there is no resonance associated with tan 2
θ
m
.
Hence we an
-
ticipate that matter effects should be helpful in fixing the mass ordering o
f
n
eutrinos. T
h
is is actua
lly
t
h
e case in so
l
ar neutrino osci
ll
ation experiments
.
I
n many astrop
h
ysica
l
environments t
h
e matter
d
ensities are not constant
.
F
or simplicity, we consider a slowly-varyin
g
matter density pro
fi
le which
fi
nd
s
proper applications both in the Sun and in some supernovae. Such a densit
y
profile allows us to make the adiabatic approximation. In this approximation
the e
ff
ective ma
g
netic
fi
eld
B
m
ch
an
g
es its
d
irection very s
l
ow
l
y, as compare
d
with the rotation o
f
P
(
t
)
around
B
m
.
Fig. 5.3 illustrates three typical stage
s
of this process, which actually takes place for neutrinos propagating in the
S
un. The situation is
q
uite di
ff
erent
f
rom the case o
f
a constant matter den
-
s
ity profile, because the initial neutrino flavor can be significantly changed
a
n
d
t
h
is c
h
an
g
e is represente
db
yt
h
epo
l
arization vector pointin
g
to t
h
e
n
e
g
at
i
ve
z
-axis as shown in Fig. 5.3
(
c
)
. One may exactly solv
e
P
z
PP
f
r
o
m
t
h
e
evolution equation in Eq.
(
5.117
)
, but its solution involves a time-dependent
coeffic
i
e
n
t
λ
(
t
)
. An intuitive interpretation of matter effects is as follows. If
the matter density and the correspondin
g
ma
g
netic field chan
g
eslowlyi
n
c
omparison with the rotation of the polarization vector, then the latter ha
s
enou
g
h time to catch up with the ma
g
netic
fi
eld and keeps the open an
g
l
e
i
ntact. Initiall
y
, the polarization vector
P
i
s almost ali
g
ned wit
h
B
m
b
ecause
5
.3 Density Matrix Formu
l
ation 193
o
f
the hi
g
h matter density at the production point. It will be ali
g
ned with
B
after the matter densit
y
decreases to zero. So
P
z
P
P
=
−
cos 2
θ
h
olds and th
e
s
urvival probability is the same as that given in Eq.
(
5.27
)
. The non-adiabatic
c
ase, which has been discussed in
S
ection 5.1.3, can also be treated in this
geometrical representation
(
Ki
m
et al., 1988
)
.
5
.
3
.2 Three-flavor Neutrino
O
scillation
s
O
ne may
g
eneralize the above density matrix
f
ormulation to describe three
-
flavor neutrino oscillations. In this more realistic case the neutrino flavor
eigenstates
(
ν
e
,ν
μ
,ν
τ
)
are linked to their mass eigenstates
(
ν
1
,
ν
2
,ν
3
)
via
a
3
×
3
un
i
tar
y
matr
i
x
V
,
which has been parametrized in Eq.
(
3.107
)
.Th
e
Majorana phases o
f
V
are irre
l
evant to neutrino osci
ll
ations an
d
t
h
us can
b
e
o
mi
tted
in
ou
r
d
i
scuss
i
o
n
s
.T
he
n
we have
⎛
⎝
⎛
⎛
ν
e
ν
μ
ν
τ
⎞
⎠
⎞
⎞
=
⎛
⎝
⎛⎛
10
0
0
c
23
s
23
0
−
s
2
3
c
23
⎞
⎠
⎞⎞
⎛
⎝
⎛⎛
c
13
0
s
13
e
−
i
δ
0
1
0
−
s
13
e
i
δ
0
c
13
⎞
⎠
⎞⎞
⎛
⎝
⎛⎛
c
12
s
12
0
−
s
12
c
12
0
001
⎞
⎠
⎞
⎞
⎛
⎝
⎛⎛
ν
1
ν
2
ν
3
⎞
⎠
⎞⎞
.
(
5.119
)
Since the CP-violating phase
δ
i
s entirely unrestricted, we may tentatively
s
witch it o
ff
.Furthermore,wede
fi
ne a convenient
fl
avor basis:
⎛
⎝
⎛⎛
ν
e
ν
x
ν
y
⎞
⎠
⎞⎞
=
⎛
⎝
⎛⎛
1
0
0
0
c
2
3
−
s
2
3
0
s
2
3
c
23
⎞
⎠
⎞⎞
⎛
⎝
⎛⎛
ν
e
ν
μ
ν
τ
⎞
⎠
⎞⎞
.
(
5.120
)
This basis is also convenient for discussing three-flavor neutrino oscillations
i
n matter,
b
ecause muon an
d
tau neutrinos
h
ave t
h
e same interactions wit
h
ordinary matter. In this basis we can write the effective Hamiltonian
H
v
as
ω
L
p
⎛
⎝
⎛
⎛
s
2
12
c
2
13
s
12
c
12
c
13
−
s
2
12
c
13
s
13
s
12
c
1
2
c
1
3
c
2
1
2
−
s
1
2
c
1
2
s
13
−
s
2
12
s
13
c
13
−
s
12
c
12
s
13
s
2
12
s
2
13
⎞
⎠
⎞⎞
+
ω
H
p
⎛
⎝
⎛⎛
s
2
13
0
c
13
s
13
000
c
13
s
13
0
c
2
13
⎞
⎠
⎞⎞
,
(
5.121
)
where
ω
H
p
≡
Δ
m
2
31
/
(2
p
)
an
d
ω
L
p
≡
Δ
m
2
21
/
(
2
p
)
are the high- and low-level
oscillation frequencies, respectively. Current experimental data yield
Δ
m
2
3
1
≈
2
.
4
×
10
−
3
e
V
2
a
n
d
Δ
m
2
21
≈
7
.
9
×
1
0
−
5
eV
2
,andthu
s
ω
H
p
ω
L
p
f
or a
g
iven
m
omentum mode. In other words
,
the term associated wit
h
ω
H
p
is ex
p
ected t
o
be dominant in Eq.
(
5.121
)
. In this case the three-flavor neutrino oscillation
s
c
an approximate to the two-
fl
avor neutrino oscillations with the hi
g
h-leve
l
f
requenc
y
ω
H
p
and the mixing angl
e
θ
13
.
Such an a
pp
roximation has been
extensively adopted in the study of flavor conversions of supernova neutrino
s
(
Hannestad
et al
., 2006; Duan
et al
., 2006; Fo
g
l
i
et al
.
,
2007
)
.
I
n the case of three-flavor neutrino mixing we have to deal with some 3
×
3
H
ermitian matrices, such as the density matrix and the e
ff
ective Hamiltonian
.
It is well known that an arbitrar
y
3
×
3 Hermitian matrix can be ex
p
ande
d
i
n terms of the identity matrix and eight Gell-Mann matrices
:
1
94 5 Phenomenology o
f
Neutrino
O
scillations
Λ
0
=
⎛
⎝
⎛⎛
100
0
10
001
⎞
⎠
⎞⎞
,Λ
1
=
⎛
⎝
⎛⎛
010
1
00
000
⎞
⎠
⎞
⎞
,Λ
2
=
⎛
⎝
⎛⎛
0
−
i
0
i
0
0
000
⎞
⎠
⎞⎞
,
Λ
3
=
⎛
⎝
⎛⎛
100
0
−
10
0
00
⎞
⎠
⎞⎞
,Λ
4
=
⎛
⎝
⎛⎛
001
000
1
00
⎞
⎠
⎞⎞
,Λ
5
=
⎛
⎝
⎛⎛
00
−
i
00 0
i
00
⎞
⎠
⎞⎞
,
Λ
6
=
⎛
⎝
⎛⎛
000
001
0
10
⎞
⎠
⎞⎞
,Λ
7
=
⎛
⎝
⎛⎛
00 0
00
−
i
0
i0
⎞
⎠
⎞⎞
,Λ
8
=
1
√
3
⎛
⎝
⎛⎛
10 0
01 0
00
−
2
⎞
⎠
⎞⎞
,
(
5.122
)
where the normalization of the Gell-Mann matrices is taken to be Tr
[
Λ
a
Λ
b
]=
2
δ
ab
(
fo
r
a
,
b
=
1
,
2
,
···
,
8)
. Note that the Gell-Mann matrices satisfy the
SU
(
3
)
Lie algebra; i.e.,
[
Λ
a
,Λ
b
]
=
c
i
f
abc
ff
Λ
c
.
H
e
r
ethest
r
uctu
r
eco
n
sta
n
ts
f
abc
f
f
a
re antisymmetric wit
h
respect to any two in
d
ices, an
d
t
h
ose nonzero
ones are
g
iven by
f
12
3
2
=
f
1
4
7
=
f
165
=
f
246
ff
=
f
257
ff
=
f
345
ff
=
f
376
f
f
=
f
458
ff
√
3
=
f
678
ff
√
3
=
1
.
(
5.123
)
A
n arbitrary
3
×
3H
ermitian matrix
M
can t
h
en
b
eexpan
d
e
d
as
M
=
1
3
M
0
M
M
Λ
0
+
1
2
M
·
Λ
≡
1
3
M
0
MM
Λ
0
+
1
2
8
a
=1
M
a
M
Λ
a
,
(
5.124
)
w
h
e
r
e
M
0
MM
=
Tr
[
MΛ
0
]
an
d
M
a
M
=
Tr
[
MΛ
a
](
fo
r
a
=1
,
2
,
···
,
8
)
.Noww
e
work in an eight-dimensional vector space spanned by eight unit vectors
e
a
,
s
o any vector
M
can
b
e represente
db
y its component
s
M
a
M
(
i.e.
,
M
=
M
1
e
1
+
···
+
M
8
M
M
e
8
)
.Bymeansofthislanguage,wehav
e
H
v
=
ω
p
1
3
B
0
Λ
0
+
1
2
B
·
Λ
,
(
5.125
)
where
ω
p
≡
|
Δ
m
2
31
|
/
(2
p
)
>
0; and the “magnetic field B”isgivenby
B
=2
εs
12
c
12
c
13
e
1
+
s
2
13
−
ε
(
c
2
1
2
−
s
2
12
c
2
13
)
e
2
+
2
(
1
−
ε
s
2
1
2
)
s
13
c
13
e
4
−
2
ε
s
12
c
12
s
13
e
6
+
1
2
√
3
(
ε
−
2)(3
c
2
13
−
1)
+
3
ε
s
2
13
(2
c
2
13
−
1)
e
8
(
5.126
)
w
i
th
ε
≡
Δ
m
2
21
/
Δ
m
2
3
1
.
O
ne has
ε>
0f
or
Δ
m
2
3
1
>
0
an
d
ε<
0f
or Δ
m
2
3
1
<
0. In the latter case an overall minus si
g
n should be introduced into the
ex
p
ression of
B
.
The three-flavor density matri
x
ρ
canbewrittena
s
ρ
(
t
)
=
1
3
Λ
0
+
1
2
P
(
t
)
·
Λ
,
(
5.127
)
where Tr
[
ρ
]
= 1 holds as the normalization condition. Eqs.
(
5.125
)
and
(
5.127
)
a
llow one to work out the evolution e
q
uation of the
p
olarization vecto
r
P
(
t
)
:

5
.3 Density Matrix Formu
l
ation 195
d
d
t
P
(
t
)
=
ω
p
B
×
P
(
t
)
≡
ω
p
8
a
=1
8
b
=
1
f
abc
ff
B
a
P
b
PP
(
t
)
e
c
,
(
5.128
)
which is a direct generalization of Eq.
(
5.111
)
to the three-flavor case. I
n
order to understand the physical meanin
g
o
f
P
(
t
)
, we consider a beam of
ν
α
n
eutrinos in the pure flavor state propagating in vacuum. The state vector
o
f
this system can be written as
|
Ψ
(
t
)
=
a
e
(
t
)
|
ν
e
+
a
μ
(
t
)
|
ν
μ
+
a
τ
(
t
)
|
ν
τ
,
a
nd the densit
y
matrix is de
fi
ned a
s
ρ
(
t
)
=
|
Ψ
(
t
)
Ψ
(
t
)
|
. The dia
g
onal matri
x
elements of
ρ
(
t
)
are given b
y
ρ
ββ
=
|
a
β
|
2
(
for
β
=
e, μ,
τ
)
. They are just the
probabilities o
f
ν
α
→
ν
β
ν
o
sci
ll
ations. More exp
l
icit
l
y, we o
b
tain
P
(
ν
α
→
ν
e
)
=
1
3
+
1
2
P
3
P
P
+
1
√
3
P
8
P
P
,
P
(
ν
α
→
ν
μ
)
=
1
3
−
1
2
P
3
P
P
−
1
√
3
P
8
P
P
,
P
(
ν
α
→
ν
τ
)
=
1
3
−
1
√
3
P
8
PP
.
(
5.129
)
N
ote that different initial flavors correspond to different initial conditions o
f
the
p
olarization vector. I
f
the initial state is an electron neutrino,
f
or instance,
the nonzero com
p
onents of
P
(
0
)
will b
e
P
3
PP
(
0
)
=1an
d
P
8
PP
(
0
)
=1
/
√
3
.
W
e
remark that Eq.
(
5.129
)
hasbeenwritteninthe
(
ν
e
,ν
μ
,
ν
τ
)
basis, but the
relations obtained therein are actuall
y
independent o
f
the
fl
avor bases. The
point is that the equation of motion in Eq.
(
5.128
)
should be solved with the
c
orrespondin
g
ma
g
netic
fi
el
d
B
i
n a specific basis.
A
pictorial presentation o
f
the evolution o
f
P
(
t
)
can be done in the eight-dimensional space, but it is to
o
c
omplicated to be intuitive and instructive. Nonetheless, it is straightforward
to include matter e
ff
ects into this picture and calculate the probabilities o
f
n
eutrino oscillations by solvin
g
the evolution equation of the polarization
vector. The density matrix formulation has been used to analyze the three
-
flavor conversions of supernova neutrinos
(
Dua
n
et al
., 2008; Das
g
upta an
d
D
ighe, 2008; Dasgupt
a
e
tal., 2008; Fogli et al., 2009
)
.
5.3.3 Non-linear Evolution E
q
uations
The density matrix
f
ormulation o
f
neutrino oscillations is extremely use
f
u
l
i
n some astrophysical and cosmolo
g
ical circumstances, such as in the core-
c
o
ll
apse supernovae or in t
h
eear
l
y Universe, w
h
ere neutrinos osci
ll
ate an
d
f
requentl
y
interact with the ambient particles. But it is improper to treat
n
eutrinos as a beam of
p
articles in these cases, as we have mentioned in
Chapter 2. For instance, neutrinos from the core of a supernova have to
traverse a re
g
ion where the number densities o
f
neutrinos and antineutrino
s
a
re much hi
g
her than the number density of electrons. Hence two crucia
l
points should be noted:
(
1
)
one has to take account of the neutrino-neutrino
