Wilkinson D.J. Stochastic Modelling for Systems Biology
Подождите немного. Документ загружается.


144
CHEMICAL AND BIOCHEMICAL KINETICS
[P] to
be
a solution
of
the quadratic equation
2Keq[Pj2 +
[P]
- c =
0.
This clearly has a single positive real root given by
[P]
=
J8cKeq
+ 1 - 1.
4Keq
We can therefore find exactly the equilibrium concentrations
of
[P]
and [P
2
]
in the
absence
of
other reactions.
Alternatively, we can use the conservation equation (6.3) to reduce the pair
of
ODEs to a single first-order ODE
d[P]
2
dt
=
k2(c-
[P])-
2k1[P]
,
(6.4)
which can
be solved for given initial conditions to give the full dynanrical behaviour
of
the system.
It
turns out that (6.4) can be solved analytically to give an explicit
expression for
[P] as a function
oft,
but the solution is not elegant, and solving
ODEs is not the main focus
of
this book. Note, however, that
in
order to
be
able to do
this (analytically
or
otherwise),
we
must know both the forward and backward rate
constants k
1
and k2, and not
just
their ratio, Keq·
6.1.5 Numerical integration
of
ODEs
We will finish the section on deterministic kinetics by exanrining numerically in-
tegrate a system
of
ODEs on a computer. We will just look
at
this simplest possi-
ble technique, known as the first-order Euler method.* It is worth bearing in mind,
however, that there are more sophisticated techniques that can
be
used which give
much more accurate
dynanrics for an equivalent amount
of
computation time. A good
example
of
this is the fourth-order Runge-Kutta method, which is implemented by
many biochemical simulators.
We can write any
of
tile ODE systems tilat we have considered so far very simply
as a vector
ODE
dX
=
J(X)
dt
where X is a p-dimensionalvector
and!(·)
:
JRP
-
JRP
is an arbitrary (non-linear)
p-dimensional function
of
X.
Recall tilat tile derivative is defined by
dX
(t) = lim
X(t
+
b.t)-
X(t).
dt
L:l.t-+0
b.t
So for small b.t we have
X(t
+b.~~-
X(t)
~
f(X(t)),
* In fact, this technique is a special case
of
the Euler method for numerically solving SDEs that was
examined in
Section 5.5.

MOLECULAR APPROACH TO KINETICS
'
euler<-
function(t=50,
dt=O.OOl,
fun=f,
ic=c(l,l),
...
)
p=length(ic)
n=t/dt
xmat=matrix(O,ncol=p,nrow=n)
x=ic
xmat[l,]=x
for
(i
in
2:n)
x = x +
fun(x,
...
) *
dt
xmat[i,]=x
ts(xmat,start=O,deltat=dt)
145
Figure
6.4
An
Rfunction
to
numerically integrate a system
of
coupled ODEs using a simple
first-order Euler method
and rearranging gives
X(t
+ t:.t)
c::
X(t)
+ t:.tf(X(t)).
(6.5)
Equation ( 6.5) gives us a simple method for computing
X ( t + t:.t) from X ( t).
If
we
start off at known
X(O),
we can compute X(t:.t), X(2t:.t), X(3t:.t),
...
to get the
full dynamics
of
the system. This is the so-called Euler method.
A very simple R function to implement this algorithm is given in Figure 6.4. The
function returns an
R time series object, which can easily be plotted. For example, to
simulate the dynamics
of
the
LV
system, first define the function
lv
<-
function(x,
kl=l,
k2=0.1,
k3=0.1)
{
c(
kl*x[l]
-
k2*x[l]*x[2]
,
k2*x[l]*x[2]
-
k3*x[2]
Then typing
plot
(euler
(t=lOO,
fun=lv,
ic=c
(4,10)))
gives a plot sim-
ilar to the one shown in Figure 6.1. For more sophisticated numerical integration
strategies, consult a standard numerical analysis text such as Burden
& Faires (2000).
Note that the R package
ode
solve
(available from CRAN) provides an interface
to a fairly sophisticated
ODE solving library.
6.2 Molecular approach to kinetics
The deterministic approach to kinetics fails to capture the discrete and stochastic
nature
of
chemical kinetics at low concentrations. As many intra-cellular processes
involve reactions at extremely low concentrations, such discrete stochastic effects
are often relevant for systems biology models. We are now in a position to see how
chemical kinetics can
be
modelled in this way.

146
CHEMICAL
AND
BIOCHEMICAL
KINETICS
Consider a bi-molecular reaction
of
the form
X+Y--+?
(the RHS
is
not important). What this reaction really means is that a molecule of
X is able to react with a molecule
of
Y
if
the pair happen to collide with one an-
other (with sufficient energy), while moving around randomly, driven by Brownian
motion. Considering a single pair
of
such molecules in a container
of
volume V,
it is possible to use statistical mechanical arguments to understand the hazard of
molecules colliding. Under fairly weak assumptions regarding the container and its
contents (essentially that
it
is small or well stirred, and in thermal equilibrium), it can
be
rigorously demonstrated that the collision hazard is constant, provided the volume
is fixed and the temperature is constant. A comprehensive treatment
of
this issue
is
given in Gillespie (1992b), to which the reader is referred for further details. How-
ever, the essence
of
the argument is that as the molecules are uniformly distributed
throughout the volume and this distribution does not depend on time, then the prob-
ability that the molecules are within reaction distance is also independent
of
time. In
the case
of
time varying V (which can be quite relevant in the biological context),
the hazard is inversely proportional to
V. Again, for the careful statistical mechanical
argument see Gillespie (1992b ), but an intuitive explanation can be given as follows.
Let the molecules position in space
be
denoted by P
1
and P
2
,
respectively. Then P
1
and P
2
are uniformly and independently distributed over the volume V. This means
that for a region
of
space d with volume
v'
we have
v'
P (Pi E
d)
=
V,
i = 1,
2.
Now
if
we are interested in the probability that X and Y are within a reacting distance
(
r)
of
one another at any given instant
of
time (assuming that r is very small relative
to the dimensions
of
the container, so that boundary effects can be ignored), this
probability can be computed as
(by Proposition 3.11)
but the conditional probability will be the same for any
P
2
away from the boundary,
rendering the expectation redundant, and reducing the expression to
= P (IPI
-PI
<
r)
= P(P1
Ed)
41l'r
3
=
3V.
(for any p away from the boundary)
(where
d is a sphere
of
radius
r)
This probability is inversely proportional to V. Then conditional on the molecules
being within reaction distance, they will not necessarily react, but will do so with
a probability independent
of
V (as other important variables, such as the velocity
distributions, are independent
of
V),
thus preserving the inverse dependence on V
in the combined probability
of
being within reaction distance and reacting. The case
of
time varying V is a little messy to deal with, so a detailed discussion will be
deferred until Section 8.2.3. A fixed volume
V will be assumed throughout the rest

I
MASS-ACTION STOCHASTIC KINETICS
147
of this chapter. The case
of
non-constant temperature or other environmental factors
are
likely
not
to
have
such
a
straightforward
relationship
to
the
reaction
hazard,
and
so
again, throughout this chapter, it will be assumed that temperature, pressure, and
all other environmental factors not explicitly described in the reaction network are
held constant.
6.3 Mass-action stochastic kinetics
We
will consider a system
of
reactions involving u species X
1
,
X
2
,
...
,
Xu
and
v reactions, R
1
,
R
2
,
...
,
Rv.
Typically there will be more reactions than species,
v >
u.
We
will assume that the qualitative structure
of
the reaction network can
be encoded in the form
of
a Petri net N =
(P,
T,
Pre,
Post,
M),
where P =
(X1, X2,
...
,
Xu)'
and T = (R1, R2,
...
, Rv)',
as
described in Section 2.3.
In addition, each reaction,
R;, will have a stochastic rate constant,
q,
and an asso-
ciated
rate law (or hazard function), hi(x, ci), where x = (x1, x2,
...
, xu) is the
current state (or marking)
of
the system. The form
of
hi (x, ci) (and the interpreta-
tion
of
the rate constant ci) is determined by the order
of
reaction Ri. In all cases
the hazard function has the same interpretation, namely that conditional on the state
being
x at time t, the probability that an Ri reaction (or transition) will occur in the
time interval
(t, t +
dt]
is given by hi(x, ci) dt. Thus,
in
the absence
of
any other
reactions taking place,
the time to such a reaction event would be an
Exp(hi(x,
ci))
random quantity. Note, however, that since the hazard depends on the state x, and
other reactions could change the state, the actually time until an
Ri reaction most
likely will not be exponential at all.
6.3.1 Zeroth-order reactions
First consider a reaction
of
the form
R;:
0~X.
Although in practice things are not created from nothing, it can sometimes be useful
to
model a constant rate
of
production
of
a chemical species (or influx from another
compartment) via a zeroth-order reaction. In this case,
Ci is the hazard
of
a reaction
of this type occurring, and so
6.3.2 First-order reactions
Consider the first-order reaction
Here,
Ci represents the hazard that a particular molecule
of
Xj
will undergo the
reaction. However, there are
Xj
molecules
of
Xj,
each
of
which having a hazard
of
Ci
of
reacting. This gives a combined hazard
of
hi(X,
Ci)
=
CiXj

148
CHEMICAL AND BIOCHEMICAL KINETICS
for a reaction
of
this type. Note that first-order reactions
of
this nature are intended
to capture the spontaneous change
of
a molecule into one or more other molecules,
such as radioactive decay, or the spontaneous dissociation
of
a complex molecule
into simpler molecules.
It
is not intended to model the conversion
of
one molecule
into another in the presence
of
a catalyst, as this is really a second-order reaction.
However, in the presence of a large pool
of
catalyst that can be considered not
to
vary in level during the time evolution
of
the reaction network, a first-order reaction
may provide a reasonable approximation. Michaelis-Men ten enzyme kinetics will be
examined in detail in the next chapter.
6.3.3 Second-order reactions
For second-order reactions
of
the form
Ri:
Xj
+Xk
~?
Ci
represents the hazard that a particular pair
of
molecules
of
type
Xj
and
Xk
will
react. But since there are
Xj
molecules
of
Xj
and
Xk
molecules
of
Xk,
there are
Xj
Xk
different pairs
of
molecules
of
this type, and so this gives a combined hazard
of
hi(X,
Ci)
=
CiXj
Xk
for this type
of
reaction. There is another type
of
second-order reaction which needs
to be considered:
R:
2Xj~?
Again, Ci represents the hazard
of
a particular pair of molecules reacting. But here
there are only
xj(Xj-
1)/2 pairs
of
molecules
of
type
Xj,
and so
Xj(Xj-
1)
hi(X,
Ci)
= Ci
2
.
Note that this does not match exactly the form
of
the corresponding deterministic
mass-action rate law
-this
will be further discussed in Section 6.6.
6.3.4 Higher-order reactions
It
is straightforward to extend this theory to higher-order reactions, but in reality,
most (if not all) reactions that are normally written as a single reaction of order
higher than two, in fact represent the combined effect
of
two or more reactions
of
order one or two. In these cases it is usually better to model the reactions in detail
rather than via high-order stochastic kinetics. Consider, for example, a trimerisation
reaction
R:
3X~X3.
Taken at face value, the rate constant
Ci
should represent the hazard
of
triples of
molecules
of
X coming together simultaneously and reacting,
leading
to a rate law
of
the form
(
x)
x!
x(x-
1)(x-
2)
h(x, Ci) =
Ci
3
=
ci
(x _
3
)!
3
! =
Ci
6
.

THE
GILLESPIE
ALGORITHM
149
However, in most cases it is likely to
be
more realistic to model the process as the
pair
of
second-order reactions
2x---+
x2
X2
+X
---+ X3,
and this pair
of
second-order reactions will have quite different dynamics to the cor-
responding third-order system.
6.4 The Gillespie algorithm
The discussion in the previous sections shows that the time-evolution
of
a reaction
system can be regarded as a stochastic process. Further, due to the fact that the reac-
tion hazards depend only on the current state
of
the system (the number
of
molecules
of
each type), it is clear that the time-evolution
of
the state
of
the reaction system
can
be
regarded as a continuous time Markov process with a discrete state space.
Detailed mathematical analysis
of
such systems is usually intractable, but stochastic
simulation
of
the time-evolution
of
the system is quite straightforward.
In a given reaction system with
v reactions, we know that the hazard for a type i
reaction is
hi
( x,
Ci),
so the hazard for a reaction
of
some type occurring is
v
ho(x,
c)
=
2::::
hi(x,
Ci)·
i=l
We
now follow the discrete event stochastic simulation procedure from Section 5.4.2
to update the state
of
the process. It is clear that the time to the next reaction is
Exp(ho(x, c)), and also that this reaction will
be
a random type, picked with proba-
bilities proportional to the
hi(x,
ci). independent
of
the time to the next event. That
is, the reaction type will be
i with probability
hi(x,
Ci)/h
0
(x, c). Using the time to
the next event and the event type, the state
of
the system can
be
updated, and simu-
lation can continue. In the context
of
chemical kinetics, this standard discrete event
simulation procedure is known as
"the Gillespie algorithm" (or "Gillespie's direct
method"), after Gillespie (1977).t The algorithm can
be
summarised as follows:
The Gillespie algorithm
1.
Initialise the system at t = 0 with rate constants c
1
,
c
2
,
•..
, Cv and initial numbers
of
molecules for each species, x
1
,
x2,
...
,
Xu.
2.
For each i = 1, 2,
...
,
v,
calculate
hi(x,
ci) based on the current state, x.
3. Calculate ho(x,
c)
=
:2::~=
1
hi(x,
Ci),
the combined reaction hazard.
4. Simulate time to next event, t', as an
Exp(
ho
( x, c)) random quantity.
5.
Putt:=
t + t'.
6. Simulate the reaction index,
j,
as
a discrete random quantity with probabilities
hi(x,
Ci)
/ ho(x,
c),
i = 1, 2,
...
,
v.
t
Despite
its
publication
date,
this
paper
is
still
well
worth
reading.

150 CHEMICAL AND BIOCHEMICAL KINETICS
gillespie<-
function(N,
n,
...
)
{
tt=O
X=N$M
S=t(N$Post-N$Pre)
u=nrow(S)
v=ncol(S)
tvec=vector
("numeric",
n)
xrnat=rnatrix(O,ncol=u,nrow=n+l)
xrnat[l,)=x
for
(i
in
l:n)
{
h=N$h(x,
...
)
tt=tt+rexp(l,surn(h))
j=sarnple(v,l,prob=h)
X=X+S
(,
j)
tvec[i)=tt
xrnat[i+l,)=x
return(list(t=tvec,x=xrnat))
Figure 6.5
An
R function to implement the Gillespie algorithm
for
a stochastic Petri net
rep-
resentation
of
a coupled chemical reaction system
7. Update X according to reaction
j.
That is, put X : = X + sCj)' where
sUl
denotes
the
jth
column
of
the stoichiometry matrix S.
8.
Output x and t.
9.
Ift
<
Tmax.
return to step
2.
6.5 Stochastic
Petri
nets (SPNs)
A stochastic Petri
net
(SPN) is a Petri net where the state (represented by the number
of
tokens
at
each node) changes dynamically and randomly by choosing event firings
in a carefully prescribed random manner (Goss
& Peccoud 1998).
If
the Petri net is used to describe a chemical reaction network (Section 2.3), where
the number
of
tokens at a node represents the number
of
molecules
of
a given type,
then the rates
of
event firings are given by stochastic rate laws, and the Gillespie
algorithm can be used to determine the time to the next event firing and which event
to fire.
So a SPN is simply a convenient mathematical and graphical representation
of
a stochastic kinetic process.
A very simple R function for simulating the time-evolution
of
a SPN using the
Gillespie algorithm is given in Figure 6.5.
To
illustrate its use, consider the stochastic
kinetic formulation
of
the Lotka-Volterra system.

STOCHASTIC PETRI NETS ·(SPNS)
Here
we
will use the usual equations
leading to stochastic rate laws
Y1
~2Y1
Y1+Y2
~2Y2
y2~0
h1
(y,
c1) =
c1Y1
h2(y,
c2)
=
C2Y1Y2
h3(y, C3) = CJY2·
The SPN corresponding to this system could
be
written
N = (P,
T,
Pre,
Post,
M,
h, c), P = (Prey, Predator)',
T
= (Prey reproduction, Predator-prey interaction, Predator death)',
Pre~
G D , Poat
~
G
~)
, h(y,
e)
~
(e,y,
e,y,y,,
03
y,)'.
151
It remains only to specify the initial state
of
the system,
M,
and the vector
of
rate
constants,
c.
Some R code that formulates this problem as a SPN and then simulates
it using the Gillespie algorithm assuming initial state
M = (50, 100)' and stochastic
rate constants
c = (1, 0.005, 0.6)' is given in Figure 6.6. Note that the vector
of
rate constants is called
th
(for
())
rather than
c,
as c has special meaning in
R.
The
output from the Gillespie algorithm consists
of
a list containing two items. The first
item,
t,
is a vector
of
event times, and the second item, x, is a matrix whose rows
represent the state
of
the system immediately before the corresponding event time.
The matrix
x therefore has an additional row, corresponding to the state
of
the system
immediately
after the final event simulated. As shown in the Figure 6.6, this output
can be used to construct R
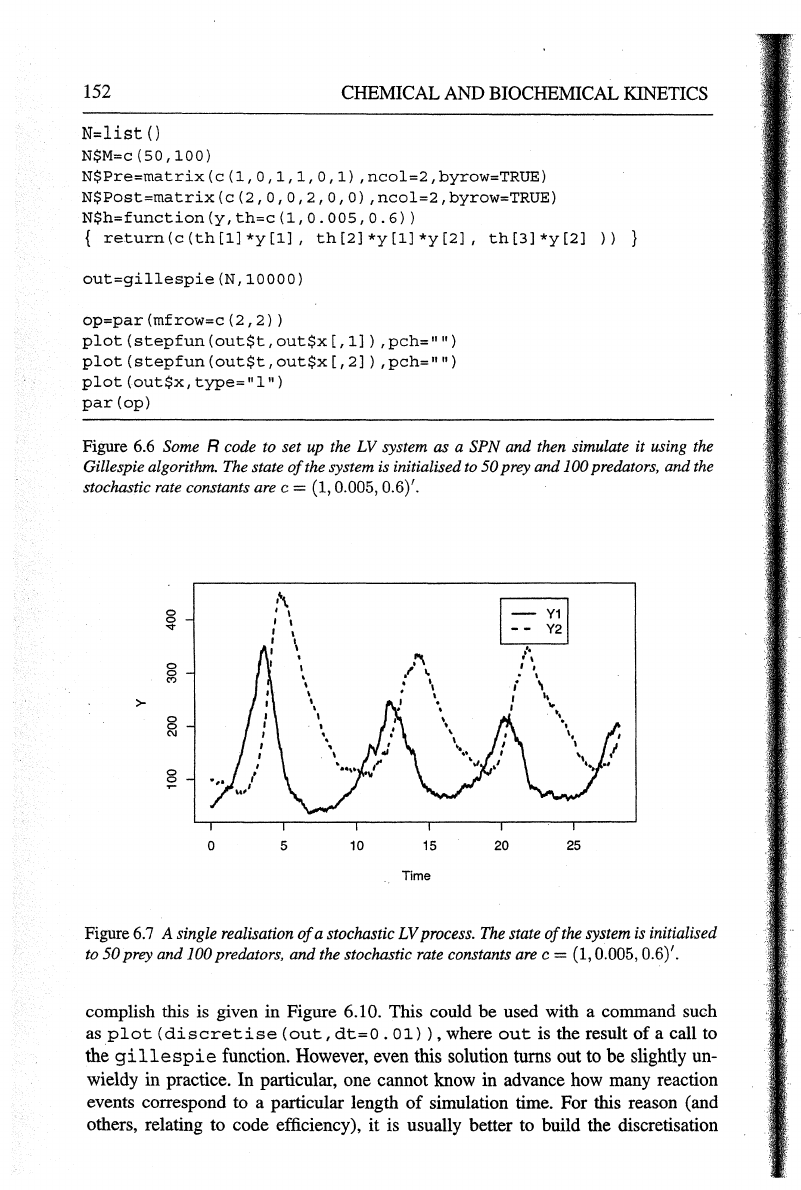
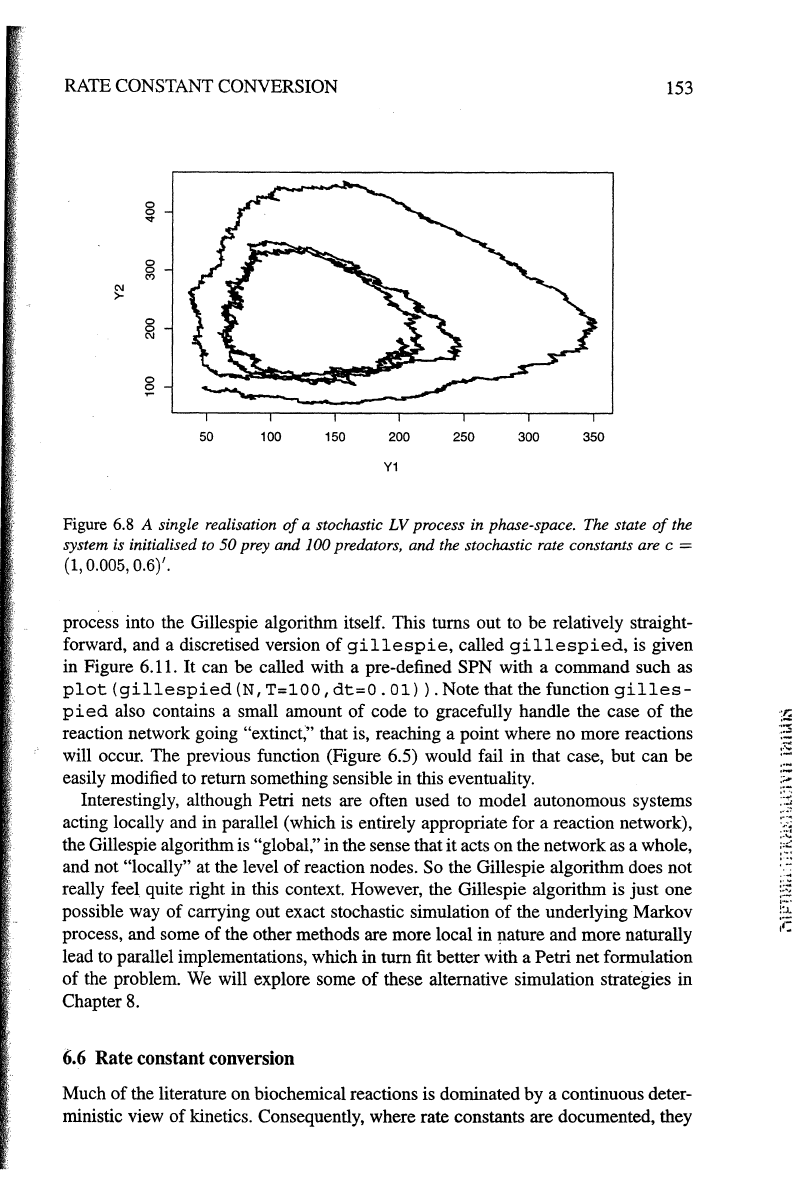
"step function" objects which can be plotted. A single
realisation
of
this process is shown in Figure 6.7 and Figure 6.8. These should
be
contrasted with the corresponding deterministic kinetics (Figure 6.1 and Figure 6.2).
It
is clear that although the stochastic solution approximately follows the path
of
the
deterministic phase-space orbits, it is not constrained to follow them slavishly, but
rather free to wander to nearby orbits in a stochastic manner.
The SBML-shorthand for this model is given in Figure 6.9, and the full
SBML
is listed in Appendix A.2 (as well as on this book's websit!!). Software suitable for
taking the
SBML as input and simulating the system dynamics will be discussed
in
Section 6.8.
Although it is sometimes useful to have output corresponding to each event that
occurs in the simulation
of
the reaction network, often this is not desirable. This
is because for systems
of
realistic size and complexity, there will
be
a very large
number
of
events, and
all
that is likely to be
of
interest is the state
of
the
sys-
tem on a relatively fine regular grid
of
time points. One approach to this prob-
lem is to time-discretise the discrete-event output
post-hoc. An R function to ac-
152
CHEMICAL
AND
BIOCHEMICAL
KINETICS
N=list
()
N$M=c
(50,
100)
N$Pre=matrix(c(l,O,l,l,O,l)
,ncol=2,byrow=TRUE)
N$Post=matrix(c(2,0,0,2,0,0),ncol=2,byrow=TRUE)
N$h=function(y,th=c(l,0.005,0.6))
{
return(c(th[l]*y[l],
th[2]*y[l]*y[2],
th[3]*y[2)
) ) }
out=gillespie(N,lOOOO)
op=par(mfrow=c(2,2))
plot(stepfun(out$t,out$x[,l]),pch="")
plot
(stepfun(out$t,out$x[,2])
,pch="")
plot(out$x,type="l")
par(op)
Figure
6.6
Some R code to set up the
LV
system
as
a
SPN
and then simulate
it
using the
Gillespie algorithm.
The
state
of
the system is initialised to
50
prey and 100 predators, and the
stochastic rate constants are c
= (1, 0.005, 0.6)'.
8
Eill
..,.
'
2
\
••
. ,
0
I I
0
'
"'
\
>-
..
..
0
..
0
•,
N
'•
\
0
~
0 5
10 15
20
25
Time
Figure
6.7
A single realisation
of
a stochastic
LV
process.
The
state
of
the system
is
initialised
to
50
prey
and
100 predators,
and
the stochastic rate constants are c = (1, 0.005, 0.6)'.
complish this is given in Figure 6.1 0. This could be used with a command such
as
plot
(discretise
(out,
dt=O.
01)),
where
out
is the result
of
a call to
the
gillespie
function. However, even this solution turns out to be slightly un-
wieldy
in practice.
In
particular, one cannot know in advance how many reaction
events correspond to a particular length
of
simulation time. For this reason (and
others, relating to code efficiency),
it
is usually better to build the discretisation
RATE
CONSTANT CONVERSION
153
50
100
150
200 250 300 350
Y1
Figure
6.8
A single realisation
of
a stochastic
LV
process in phase-space. The state
of
the
system is initialised
to
50 prey and 100 predators, and the stochastic rate constants are c =
(1, 0.005, 0.6)'.
process into the Gillespie algorithm itself. This turns out to be relatively straight-
forward, and a discretised version of
gillespie,
called
gillespied,
is given
in Figure 6.11.
It
can be called with a pre-defined SPN with a command such as
plot
(gillespied
(N,
T=lOO,
dt=O.
01)
) . Note that the function
gUles-
pied
also contains a small amount of code to gracefully handle the case
of
the
reaction network going "extinct," that is, reaching a point where no more reactions
will occur. The previous function (Figure 6.5) would fail in that case, but can be
easily modified to return something sensible in this eventuality.
Interestingly, although Petri nets are often used to model autonomous systems
acting locally and in parallel (which
is
entirely appropriate for a reaction network),
the Gillespie algorithm is
"global," in the sense that
it
acts on the network as a whole,
and not
"locally" at the level
of
reaction nodes. So the Gillespie algorithm does not
really feel quite right in this context. However, the Gillespie algorithm is just one
possible way of carrying out exact stochastic simulation
of
the underlying Markov
process, and some
of
the other methods are more local in nature and more naturally
lead to parallel implementations, which in tum fit better with a Petri net formulation
of
the problem.
We
will explore some
of
these alternative simulation strategies in
Chapter
8.
6.6
Rate
constant
conversion
Much
of
the literature on biochemical reactions is dominated by a continuous deter-
ministic view of kinetics. Consequently, where rate constants are documented, they
;;....
::;;
