Weingast B.R., Wittman D. The Oxford Handbook of Political Economy

Подождите немного. Документ загружается.

62 rational voters and political advertising

this is an unrealistic requirement, especially in a sphere of decision-making, such as

voting, which is characterized by both free riding and complexity. Agreeing with such

an objection does not imply going back to the “black box.” A microfounded model of

campaign ﬁnance need not include full Bayesian rationality. On the contrary, it would

be interesting to develop a model of campaign ﬁnance starting from non-standard as-

sumptions on the way voters make decisions. Such model could incorporate some of

the cognitive biases that are by now well documented in the psychological literature.

A non-Bayesian microfounded model of campaign ﬁnance would still be amenable

to welfare analysis, and may provide insights that are not available with rational

voters.

References

Ansolabehere,S.,andIyengar,S.1996. Going Negative: How Political Advertisements Shrink

and Polarize the Electorate. New York: Free Press.

Ashworth,S.2006. Campaign ﬁnance and voter welfare with entrenched incumbents.

American Political Science Review, 100: 41–53.

Austen-Smith,D.1987. Interest groups, campaign contributions, and probabilistic voting.

Public Choice, 54: 123–39.

Bailey,M.2004. Can representation be fair when campaign contributions come mostly from

business? An exploration in multiple dimensions. Working paper, Georgetown University.

Coate,S.2004a. Pareto improving campaign ﬁnance policy. American Economic Review, 94:

625–55.

2004b. Political competition with campaign contributions and informative advertising.

Journal of the European Economic Association, 2: 772–804.

Gerber,A.1998. Estimating the eﬀect of campaign spending on Senate election outcomes

using instrumental variables. American Political Science Review, 92: 401–11.

Grossman,G.M.,andHelpman,E.2001. Special Interest Politics. Cambridge, Mass.: MIT

Press.

Hertzendorf,M.N.1993. I’m not a high-quality ﬁrm but I play one on TV. RAND Journal of

Economics, 24: 236–47.

Kaid, L. L., and Holtz-Bacha.C.1995. Political Advertising in Western Democracies: Parties

and Candidates on Television. Beverly Hills, Calif.: Sage.

Kihlstrom,R.E.,andRiordan,M.H.1984. Advertising as a signal. Journal of Political

Economy, 92: 427–50.

Levitt,S.D.1994. Using repeat challengers to estimate the eﬀect of campaign spend-

ing on election outcomes in the US House. Journal of Political Economy, 102:

777–98.

1995. Policy watch: congressional campaign ﬁnance reform. Journal of Economic Perspec-

tives, 9: 183–94.

Milgrom,P.,andRoberts,J.1986. Price and advertising signals of product quality. Journal of

Political Economy, 94: 796–821.

Morton,R.,andCameron,C.1992. Elections and the theory of campaign contributions: a

survey and critical analysis. Economics and Politics, 4: 79–108.

andrea prat 63

Potters,J.,Sloof,R.,andvan Winden,F.1997. Campaign expenditures, contributions

and direct endorsements: the strategic use of information and money to inﬂuence voter

behavior. European Journal of Political Economy, 13: 1–31.

Prat,A.2002a. Campaign advertising and voter welfare. Review of Economic Studies, 69: 997–

1017.

2002b. Campaign spending with oﬃce-seeking politicians, rational voters, and multiple

lobbies. Journal of Economic Theory, 103: 162–89.

Schultz,C.2003. Strategic campaigns and redistributive politics. Working paper, Copen-

hagen University.

Sloof,R.1999. Campaign contributions and the desirability of full disclosure laws. Economics

and Politics, 11: 83–107.

Stratmann,T.2003. Tainted money? Contribution limits and the eﬀectiveness of campaign

spending. Working paper, George Mason University.

Vanberg,C.2004. The implications of funding asymmetries in a model of electoral competi-

tion with informative advertising and rational voting. Working paper, Cornell University.

Wittman,D.2004. Candidate quality, pressure group endorsements, and the nature of po-

litical advertising. Working paper, University of California, Santa Cruz; forthcoming in

European Journal of Political Economy.

chapter 4

..............................................................

CANDIDATE

OBJECTIVES AND

ELECTORAL

EQUILIBRIUM

..............................................................

john duggan

1 Introduction

.............................................................................

Elections, as the institution through which citizens choose their political agents,

are at the core of representative democracy, and it is therefore appropriate that they

occupy a central position in the study of democratic politics. The formal analysis of

elections traces back to the work of Hotelling (1929)andDowns(1957), who apply

mathematical methods to understand the outcomes of elections. This work, and the

literature stemming from it, has focused mainly on the positional aspects of electoral

campaigns, where we conceptualize candidates as adopting positions in a “space”

of possible policies prior to an election. In this chapter, I maintain that focus by

considering the main results for the canonical model of elections, in which candidates

adopt policy platforms simultaneously and the winner is committed to the platform

on which he or she ran. These models abstract from much of the structural detail

of elections, including primary elections, campaign ﬁnance and advertising, the role

of interest groups, etc. Nevertheless, in order to achieve a deep understanding of

elections in their full complexity, it seems we must address the equilibrium eﬀects

of position-taking by candidates in elections.

∗

I thank David Epstein, Mark Fey, Cesar Martinelli, and Martin Osborne for helpful feedback.

john duggan 65

In this chapter, I cover known foundational results on spatial models of elections,

taking up issues of equilibrium existence, the distance (or lack thereof) between the

equilibrium policy positions of the candidates, and the characterization of equilib-

ria in terms of their social welfare properties. The chapter is structured primarily

according to assumptions on voting behavior. I ﬁrst consider results for the case in

which candidates can precisely predict the behavior of voters, who are modeled in a

deterministic fashion. I refer to this as the “Downsian model.” I then consider two

models of probabilistic voting, where voting behavior cannot be precisely predicted

by the candidates and is modeled as a random variable. Within each section, I con-

sider the most common objective functions used to model the electoral incentives of

diﬀerent types of candidates, including candidates who seek only to win the election,

candidates who seek to maximize their share of the vote, and candidates who seek the

best policy outcome from the election.

Of several themes in the chapter, most prominent is the diﬃculty in obtaining

existence of equilibrium, especially when the policy space is multidimensional. As

a point of reference for the existence issue, early articles by Debreu (1952), Fan

(1952), and Glicksberg (1952) give useful suﬃcient conditions for existence of equi-

libriuminthegamesweanalyze.

Their existence result, which we will refer to

as the “DFG theorem,” ﬁrst assumes each player’s set of strategies is a subset of



that is non-empty, compact (so it is described by a well-deﬁned boundary in



), and convex (so a player may move from one strategy toward any other with

no constraints). These regularity assumptions are easily satisﬁed in most models.

Second, and key to our analysis, DFG assumes that the objective function of each

player is:

jointly continuous in the strategies of all players (so small changes in the strate-

gies of the players lead to small changes in payoﬀs)

quasi-concave in that player’s own strategy, given any strategies for the other

players (so any move toward a better strategy increases a player’s payoﬀ).

These continuity and convexity conditions are typically violated in electoral models.

We will see that in some cases existence of equilibrium can be obtained despite this

obstacle, but in many cases it cannot.

The well-known median voter theorem establishes that there is a unique equi-

librium in the unidimensional Downsian model, and in it both candidates locate

at the median of the voters’ ideal policies. When the policy space is multidimen-

sional, however, equilibria typically do not exist in the Downsian model. Probabilistic

voting smooths the objective functions of the candidates and is commonly thought

to mitigate the existence problem. We will give reasonable (if somewhat restrictive)

conditions under which this is true for vote-motivated candidates, but, due to non-

convexities in other models, probabilistic voting can actually introduce non-existence

of equilibrium, even in one dimension.

¹Nash1950 proves existence of mixed strategy equilibrium for ﬁnite games. Since our games involve

convex (and therefore inﬁnite) policy spaces, his result does not apply here.

66 candidate objectives and electoral equilibrium

2 The Electoral Framework

.............................................................................

We will focus on the spatial model of politics, as elaborated by Davis, Hinich, and

Ordeshook (1970), Ordeshook (1986), and Austen-Smith and Banks (1999). Here, we

assume that the policy space X is a subset of Euclidean space of some ﬁnite dimension,

d. Thus, a policy is a vector x =(x

,...,x

), where x

may denote the amount

of spending on some project or a position on some issue, suitably quantiﬁed. We

assume that X is non-empty, compact, and convex. We consider an election with

just two political candidates, A and B (sometimes interpreted as parties), and we

analyze an abstract model of campaigns: we assume that the candidates simultane-

ously announce policy positions x

and x

in the space X, and we assume that the

winning candidate is committed to his or her campaign promise. Following these

announcements, a ﬁnite, odd number n of voters, denoted i =1, 2,...,n,casttheir

ballots b

∈{1, 0},whereb

= 1 denotes a vote for candidate A and b

=0denotes

a vote for B, the winner being the candidate with the most votes. We do not allow

abstention by voters.

To describe the various objectives attributed to candidates in the literature, let

, x

, b

,...,b

) denote candidate A’s utility when the candidates take po-

sitions x

and x

and the vector of ballots is (b

,...,b

). Deﬁne the notation

, x

, b

,...,b

) similarly. The ﬁrst main approach to modeling candidate ob-

jectives is to view the candidates as primarily concerned with their electoral prospects.

Accordingly, our ﬁrst objective function dictates that a candidate cares only about

whether he or she garners a majority of votes. In other words, only the sign, rather

than the magnitude, of the margin of victory matters.

Win motivation. The candidates receive utility equal to one from winning, zero

otherwise, so that

, x

, b

,...,b



1if



0if



with candidate B’s utility equal to one minus the above quantity.

The second objective function also captures the idea that candidates care primarily

about electoral success, but now measured in the number of votes for the candidate.

Vote motivation. The candidates’ utilities take the simple linear form

, x

, b

,...,b



with candidate B’s utility being n −



By the term oﬃce motivation, we refer to the situation in which either both can-

didates are win motivated or both are vote motivated. The second main approach to

² Note that, since we rule out abstention by voters, vote motivation is equivalent by a positive aﬃne

transformation to plurality motivation: the margin of victory for candidate A, for example, is just



) −n.

john duggan 67

modeling candidate objectives is to assume that candidates care only about the policy

outcome of the election.

Policy motivation. Assume the candidates have policy preferences represented by

strictly concave, diﬀerentiable utility functions u

and u

. In words, the graphs of

these utility functions are smooth and “dome shaped.” Under these assumptions,

each candidate has an ideal policy, which yields a strictly higher utility than all other

policies, and we denote these as

and

. We assume these ideal policies are distinct,

so that

=

. Then candidate A’s utility from policy positions x

and x

and

ballots (b

,...,b

)is

, x

, b

,...,b



)if



)if



and likewise for candidate B.

To model voting behavior, let P

, x

) denote the probability that voter i

votes for candidate A, i.e. casts ballot b

= 1, given policy platforms x

and x

The probability of a vote for candidate B is then 1 − P

, x

). This represen-

tation of voting behavior allows for voters to vote in a deterministic fashion or,

perhaps reﬂecting a lack of information on the candidates’ parts, in a probabilis-

tic way. Finally, let P (x

, x

) denote the probability that candidate A wins the

election, given the individual vote probabilities. Of course, B’s probability of win-

ning is one minus this amount. We assume that candidates are expected util-

ity maximizers, so that candidate A seeks to maximize E [U

, x

, b

,...,b

)],

where the expectation is taken over vectors of ballots (b

,...,b

) with respect to

the distribution induced by the P

, x

) probabilities, and likewise for candi-

date B. If we “integrate out” the vector of ballots, we may write expected utili-

ties as functions EU

, x

)andEU

, x

) of the candidates’ policy positions

alone.

Given these expected utilities, we may subject the electoral model to an equi-

librium analysis to illuminate the locational incentives of the candidates. We say a

pair (x

∗

, x

∗

) of policy platforms is an equilibrium if neither candidate can gain by

unilaterally deviating, i.e. we have

(y, x

∗

) ≤ EU

∗

, x

∗

)andEU

∗

, y) ≤ EU

∗

, x

∗

)

for all policies y.

3 The Downsian Model

.............................................................................

We now specify voting behavior, following Downs (1957) and others, by assuming

that voters vote in an essentially deterministic fashion as a function of the can-

didates’ platforms: each voter simply votes for the candidate who oﬀers the best

68 candidate objectives and electoral equilibrium

political platform, voting in a random way (by ﬂipping a fair coin) only when

indiﬀerent.

Downsian model. We assume that each voter i has preferences over policies rep-

resented by a utility function u

satisfying strict concavity and diﬀerentiability (the

same conditions imposed on candidate utilities under policy motivation). Under

these assumptions, voter i has a unique ideal policy, denoted

, which yields a strictly

higher utility than any other policy. A common special case is quadratic utility, in

which a voter cares only about the distance of a policy from his or her ideal policy,

e.g. u

(x)=−||x −

for all x (where || · || is the usual Euclidean norm). In this

case, the voters’ indiﬀerence curves take the form of concentric circles centered at

the ideal policy. For convenience, we assume that the ideal policies of the voters are

distinct. We assume a voter votes for the candidate with the preferred policy position,

randomizing only in case of indiﬀerence, i.e.

, x

⎧

⎨

⎩

1ifu

) > u

)

0ifu

) < u

)

else.

This assumption may be interpreted as “sincere” voting. Assuming voting is costless,

it is consistent with elimination of weakly dominated voting strategies in the voting

game.

3.1 Oﬃce Motivation

In the Downsian model, win motivation takes the following simple form:

, x

⎧

⎨

⎩

1if#{i | u

) > u

)} > #{i | u

) > u

)}

0if#{i | u

) > u

)} > #{i | u

) > u

)}

else,

and likewise for candidate B, while the alternative of vote motivation is

, x

)=#{i | u

) > u

)}+

#{i | u

)=u

)},

and likewise for B. The distinction between these two formalizations of oﬃce moti-

vation is actually irrelevant for the equilibrium analysis under deterministic voting,

and we state our results in terms of oﬃce motivation generally.

It is easy to see that both objectives are marked by discontinuities and non-

convexities, so that both of the conditions needed for the DFG theorem are violated.

For example, Figure 4.1 depicts the indiﬀerence curves of three voters through a

policy x, along with their ideal policies. If candidate B, say, locates at the policy x,

then candidate A obtains a majority of votes by locating in any of the three shaded

“leaves.” The candidate’s utility under win motivation from locating at x



is zero,

and it is one at x



. Now consider A’s utility when moving from x



directly to x



when the candidate enters the shaded leaf, the utility jumps up discontinuously to

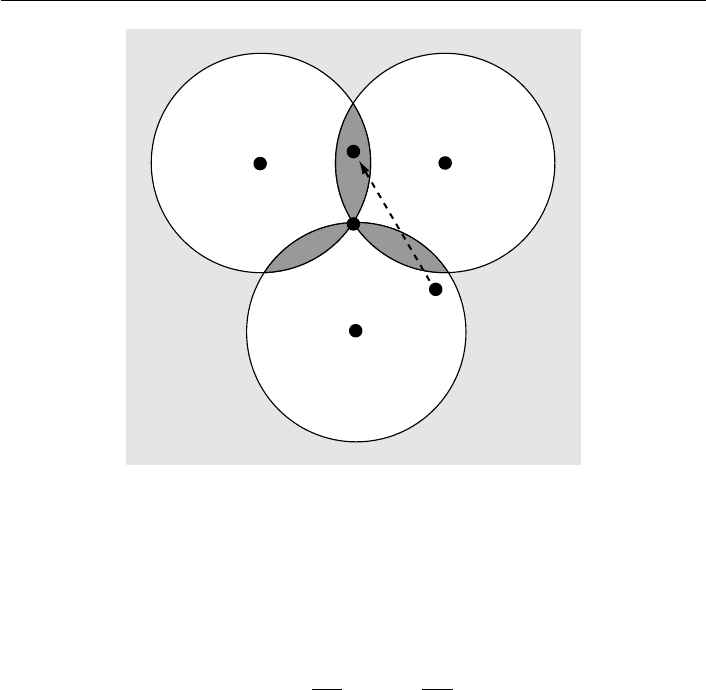
john duggan 69

x''

Fig. 4.1 Discontinuity and non-convexity

one (violating continuity); it then jumps back down to zero and then back up to

one (violating quasi-concavity) before reaching x



. Similar observations hold for vote

motivation.

The formal equilibrium analysis of the model relies on the concept of the

“gradient” of a voter’s utility function, the vector

∇u

(x)=



∂u

∂x

(x),...,

∂u

∂x

(x)



pointing in the direction of steepest ascent of the voter’s utility at a policy x.Adirect

implication of Plott’s (1967) social choice analysis of majority voting is that there is at

most one equilibrium, and that this equilibrium (if it exists) is characterized by two

conditions: both candidates locate at the ideal policy of some voter, and the gradients

of the voters at that policy must be paired in such a way that, for every voter whose

gradient points in one direction from the ideal policy, there is exactly one voter whose

gradient points in the opposite direction. The latter condition is referred to as “radial

symmetry” and is depicted in Figure 4.2,wherevoter1’s gradient is diametrically

opposed to voter 2’s.

Theorem 1: (Plott): In the Downsian model, assume oﬃce motivation. There is at

most one equilibrium. The platform pair (x

∗

, x

∗

) is an equilibrium if and only if (i)

there is a voter k such that the candidates locate at k’s ideal policy, i.e. x

∗

and (ii) radial symmetry holds at

,i.e.eachvoteri= k can be associated with a

voter j =k(ina1–1 way) so that ∇u

(

x) points in the direction opposite ∇u

(

x).

The most common application of the Downsian model is the unidimensional

model, where policies represent positions on a single salient issue. In this case,

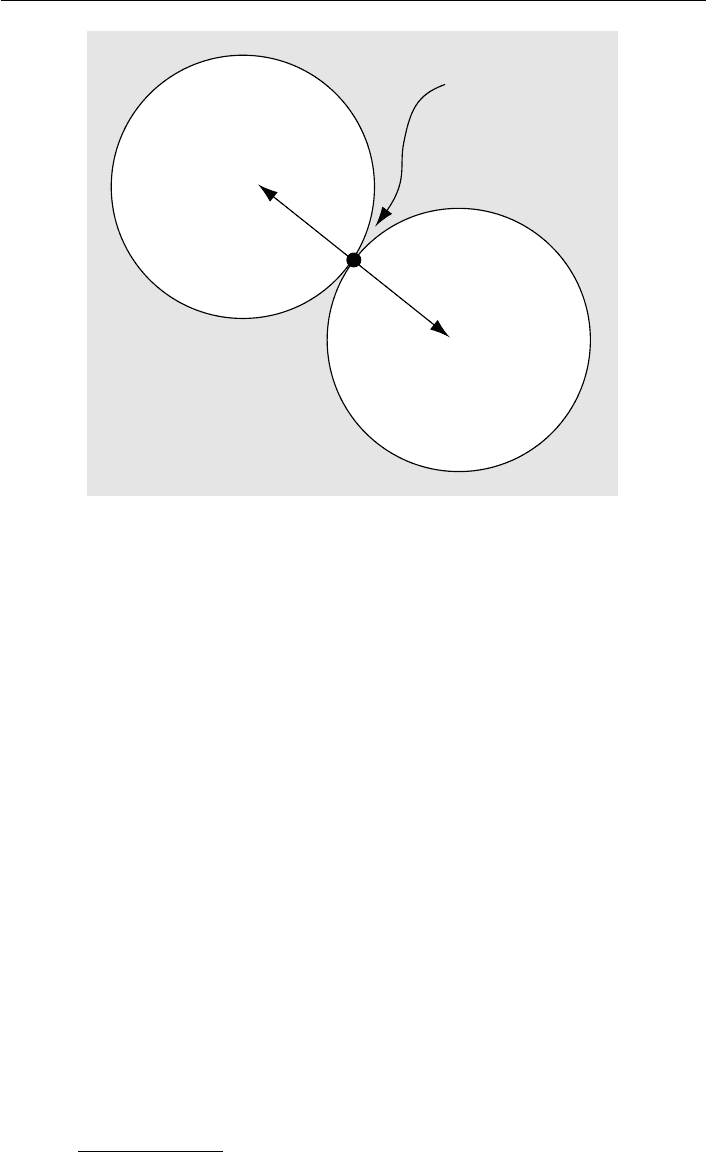
70 candidate objectives and electoral equilibrium

∆

) = 0

)

∆

Fig. 4.2 Radial symmetry in equilibrium

Theorem 1 implies that there is a unique equilibrium, and in equilibrium the can-

didates both locate at the median ideal policy. Known as the “median voter theorem,”

this connection was made by Hotelling (1929) in his model of spatial competition and

by Downs (1957) in his classic analysis of elections.

Corollary 1: (Hotelling; Downs): In the Downsian model, assume X is unidimen-

sional and oﬃce motivation. There is a unique equilibrium, and in equilibrium the

candidates locate at the median ideal policy.

When the policy space is multidimensional, the necessary condition of radial

symmetry becomes extremely restrictive—so restrictive that it will be violated for

almost all speciﬁcations of voter preferences, with the implication that equilibria will

almost never exist. And if there were an equilibrium, as in Figure 4.2,thenarbitrarily

small perturbations of voter preferences could break radial symmetry, implying that

existence is a “razor’s edge” phenomenon.

3.2 Policy Motivation

The objective function representing policy motivation takes the form

, x

⎧

⎪

⎨

⎪

⎩

)if#{i | u

) > u

)} > #{i | u

) > u

)}

)if#{i | u

) > u

)} > #{i | u

) > u

)}

)+u

)

else

john duggan 71

in the Downsian model. The above objective function also suﬀers from discontinu-

ities and non-convexities, but it diﬀers fundamentally from the oﬃce motivation in

other ways. Nevertheless, Roemer (1994) proves a median voter theorem for policy

motivation, and Wittman (1977)andCalvert(1985) prove related results for multidi-

mensional policy spaces and Euclidean preferences that yield the median voter result

in the special case of one dimension. As with oﬃce motivation, there is a unique

equilibrium, and in equilibrium both candidates locate at the median ideal policy.

Theorem 2: (Wittman; Calvert; Roemer): In the Downsian model, assume X is

unidimensional and policy motivation. If

, then there is a unique equi-

librium (x

∗

, x

∗

). In equilibrium, the candidates locate at the median ideal policy:

∗

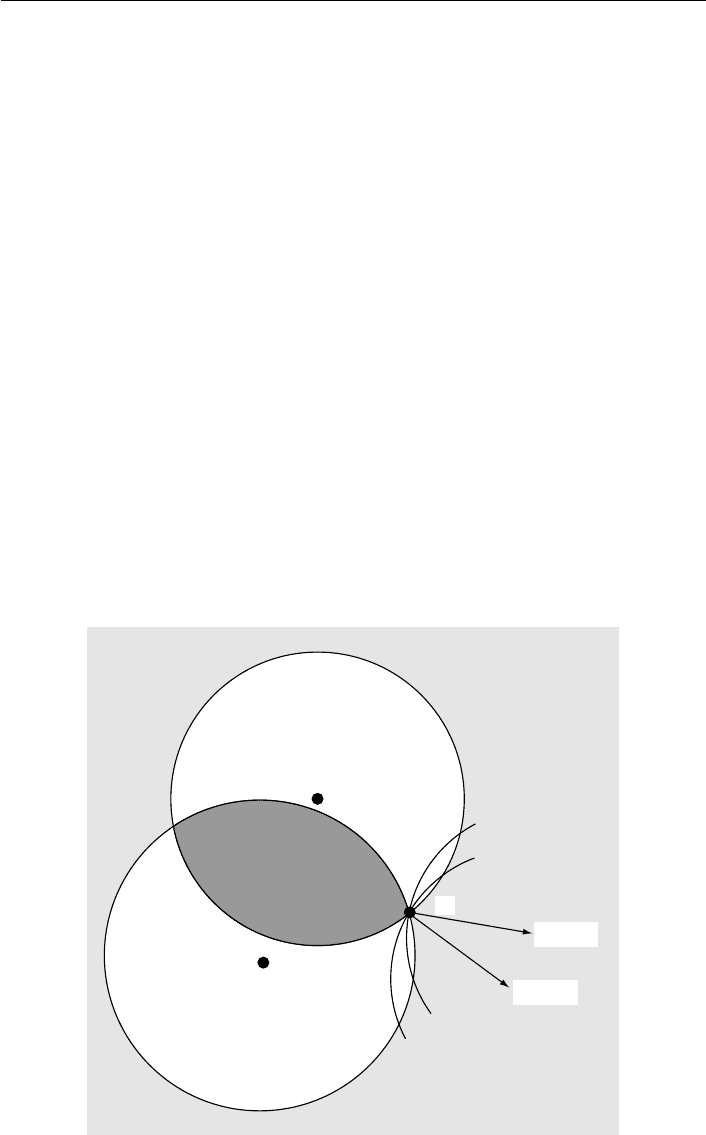
Theorem 2 leaves open the question of whether equilibria exist when the policy

space is multidimensional. Duggan and Fey (2005a) give the example depicted in Fig-

ure 4.3, where there is no equilibrium under win motivation, yet it is an equilibrium

under policy motivation for the candidates to locate at voter 3’s ideal policy: as the

candidates’ indiﬀerence curves suggest, neither can move to a position that beats

in a majority vote (the shaded area in the ﬁgure) and is preferable to

.Furthermore,

this equilibrium is robust to small perturbations in the preferences of voters and

candidates, suggesting more positive results on equilibrium existence under policy

motivation.

)

∆

Fig. 4.3 Equilibrium with policy motivation but not win motivation