Wegener I. Complexity Theory. Exploring the Limits of Efficient Algorithms

Подождите немного. Документ загружается.

3.3 The Fundamental Complexity Classes for Algorithmic Problems 31

Theorem 3.3.1. EP = ZPP(1/2).

Proof.

EP ⊆ ZPP(1/2): If a problem belongs to EP, then there is a randomized

algorithm that correctly solves this problem and for every input of length n

has an expected runtime that is bounded by a polynomial p(n). The Markov

Inequality (Theorem A.2.9) says that the probability of a runtime bounded

by 2 · p(n)isatleast1/2. So we will stop the algorithm if it has not halted on

its own after 2 · p(n) steps. If the algorithm stops on its own (which it does

with probability at least 1/2), then it computes a correct result. If we stop

the algorithm because it takes too long, we will interpret this as a failure and

output “?”. By deﬁnition, this modiﬁed algorithm is a

ZPP(1/2) algorithm.

ZPP(1/2) ⊆ EP: If a problem belongs to ZPP(1/2), then there is a random-

ized algorithm with worst-case runtime bounded by a polynomial p(n)that

never gives false results and provides the correct result with probability at

least 1/2. We can repeat this algorithm independently as often as necessary

until it produces a result, which will then necessarily be correct. By Theo-

rem A.2.12 the expected number of repetitions is bounded by 2. In this way

we obtain a modiﬁed algorithm that always provides correct results and has

a worst-case expected runtime bounded by 2 · p(n). This is an

EP algorithm.



On the basis of this theorem we will only consider worst-case runtime and

various types of error-probabilities. The notation

EP is unusual, and we have

only used it temporarily. In the future we will consider only the

ZPP-classes

instead.

ZPP(1/2) algorithm is like a coin toss in which we lose with probability

at most 1/2. If we repeat the coin toss several times, we will hardly ever lose

every toss. For

ZPP algorithms, one successful run without failure is suﬃcient

to know the correct result (with certainty). This observation can be gener-

alized to drastically reduce the failure-rate. This is referred to as probability

ampliﬁcation.

Theorem 3.3.2. Let p(n) and q(n) be polynomials, then

ZPP(1 − 1/p(n)) = ZPP(2

−q(n)

Proof. We will repeat an algorithm with failure-rate of 1 − 1/p(n) a total of

t(n) times, whereby the individual runs are fully independent, i.e., each new

run uses new random bits. If all of the runs fail, then our new algorithm fails.

Otherwise, every run that does not fail outputs a correct result, which we can

recognize because it diﬀers from “?”. The new algorithm can output any one

of these correct results. The failure-rate of the new algorithm is

(1 − 1/p(n))

t(n)

We let t(n):=(ln 2)·p(n)·q(n). Then t(n) is a polynomial, so the runtime of

the new algorithm is polynomially bounded. Furthermore, since (1 −

)

≤

32 3 Fundamental Complexity Classes

−1

,wehave

(1 − 1/p(n))

(ln 2)·p(n)·q(n)

≤ e

−(ln 2)·q(n)

−q(n)

. 

To reduce the failure-probability from 1 − 1/n to 2

−n

, fewer than n

repe-

titions of the algorithm are required. Smaller failure-probabilities than 2

−q(n)

are impossible with polynomially bounded runtimes. If the computation time

is bounded by a polynomial t(n), then there are at most t(n) random bits,

and so at most 2

t(n)

diﬀerent random sequences. Thus, if the algorithm fails

at all, it must fail with probability at least 2

−t(n)

. Because they only allow

polynomially bounded computation time, the

ZPP(ε(n))-classes for all ε(n)

that do not approach 1 suﬃciently quickly and are not equivalent to ε(n)=0

collapse to the same class. Thus we obtain the following complexity classes.

Deﬁnition 3.3.3. An algorithmic problem belongs to the complexity class

ZPP

if it belongs to ZPP(1/2), that is, if there is an algorithm with polynomially

bounded worst-case runtime that never produces incorrect results and for every

input has a failure-probability bounded by 1/2. An algorithmic problem belongs

ZPP

∗

if it belongs to ZPP(ε(n)) for some function ε(n) < 1.

ZPP algorithms are of practical signiﬁcance, since the failure-probability

can be made exponentially small. On the other hand,

ZPP

∗

algorithms that

are not

ZPP algorithms have no direct practical signiﬁcance. Nevertheless, we

will encounter the complexity class

ZPP

∗

again later and give it another name.

Our considerations in the proof of Theorem 3.3.2 can be extended to

algorithms. If we repeat an RP(ε(n)) algorithm t(n) times, every input that

should be rejected will be rejected in each repetition. On the other hand,

for inputs that should be accepted, the probability of being rejected in every

repetition is bounded by ε(n)

t(n)

. So we will make our decision as follows: If

at least one repetition of the

RP algorithm accepts, then we will accept; if all

repetitions reject, then we will reject. Then the proof of Theorem 3.3.2 leads

to the following result.

Theorem 3.3.4. Let p(n) and q(n) be polynomials, then

RP(1 − 1/p(n)) = RP(2

−q(n)

). 

The number of repetitions required is exactly the same as it was for the

ZPP algorithms.

Deﬁnition 3.3.5. A decision problem belongs to the complexity class

RP if it

belongs to the class

RP(1/2), that is, if there is a randomized algorithm with

polynomially bounded worst-case runtime that rejects every input that should

be rejected with probability 1 and has an error-probability bounded by 1/2 for

inputs that should be accepted. A decision problem belongs to

∗

if it belongs

RP(ε(n)) for some function ε(n) < 1.

3.3 The Fundamental Complexity Classes for Algorithmic Problems 33

Once again, RP algorithms and co-RP algorithms – like the primality test

we discussed previously – are of practical signiﬁcance, and the complexity

class

∗

will prove to be central for complexity theory and will later receive

a diﬀerent name.

The idea of reducing the error-probability by means of independent repe-

titions is not so easily extended to

BPP(ε(n)) algorithms, since we can never

be sure that a result is correct. If we consider an input x of length n then we

get a correct result with probability of s := s(x) ≥ 1 − ε(n) > 1/2. For t(n)

independent runs, we expect a correct result in s · t(n) >t(n)/2 of the tries.

In general, for a search problem we could obtain t(n) diﬀerent results and

have no idea which result we should choose. For problems that have a single

correct result the situation is better. We can take a majority vote,thatis,we

can choose the result that appears most often among the t(n) repetitions of

the algorithm. This majority decision is only wrong if fewer than t(n)/2of

the repetitions deliver the correct result. We can analyze this situation using

the Chernoﬀ Inequality (Theorem A.2.11). Let X

=1iftheith repetition

delivers the correct result, otherwise let X

=0.ThenProb(X

=1)=s,the

random variables X

,...,X

t(n)

are fully independent, and E(X)=s · t(n)for

X = X

+ ···+ X

t(n)

Prob(X ≤ t(n)/2) = Prob(X ≤ (1 − (1 − 1/(2s))) · E(X)) .

When applying the Chernoﬀ Inequality, δ =1− 1/(2s)and

Prob(X ≤ t(n)/2) ≤ e

−t(n)·s·δ

Since s ≥ 1 − ε(n), this bound is largest when s =1− ε(n).

For t(n):=(2 · ln 2) · q(n) · p(n)

, i.e., a polynomial, we obtain an error-

probability that is bounded by 2

−q(n)

. For most optimization problems we

can determine in (deterministic) polynomial time if two results have the same

quality. Since the value of the optimal solution is unique, we can in this case

reduce the error-probability in an analogous manner.

Theorem 3.3.6. Let p(n) and q(n) be polynomials. If we restrict our atten-

tion to the class of problems with a unique solution or to optimization problems

for which the value of a solution can be computed in polynomial time, then

BPP(1/2 − 1/p(n)) = BPP(2

−q(n)

) . 

Theorem 3.3.6 covers the cases that are most interesting to us. Therefore,

the following deﬁnitions are justiﬁed.

Deﬁnition 3.3.7. An algorithmic problem belongs to the complexity class

BPP

if it belongs to BPP(1/3), that is, if there is a randomized algorithm with

polynomially bounded worst-case runtime such that the error-probability for

each input is bounded by 1/3. An algorithmic problem belongs to

PP if it

belongs to

BPP(ε(n)) for some function ε(n) < 1/2.

34 3 Fundamental Complexity Classes

The designation “bounded-error” refers to the fact that the error-prob-

ability has at least some constant distance from 1/2. The class

BPP(1/2) is

just as senseless as the class

ZPP(1), since it contains all decision problems,

even non-computable ones.

We repeat the deﬁnitions of our complexity classes

P, ZPP, ZPP

∗

, RP,

∗

, co-RP, co-RP

∗

, BPP ,andPP informally. All of these classes assume a

polynomially bounded worst-case runtime for their respective (randomized)

algorithms. For the class

P, the result of the algorithm must always be correct,

so we have no need for random bits. For the classes

ZPP and ZPP

∗

errors are

forbidden, but the algorithms may fail to give an answer. On the other hand,

for the classes

RP, RP

∗

, co-RP,andco-RP

∗

a one-sided error is allowed – for

RP and RP

∗

only if x ∈ L, and for co-RP and co-RP

∗

only if x ∈ L. Finally,

for

BPP and PP there may be an error on any input. ZPP, RP, co-RP,andBPP

are complexity classes with bounded failure- or error-probabilities, while the

classes

ZPP

∗

, RP

∗

, co-RP

∗

,andPP are complexity classes without reasonable

bounds on the failure- or error-probabilities.

Algorithms with bounded failure- or error-probability lead to algorithms

that are reasonably applicable in practice. Thus the complexity classes

P, ZPP, RP, co-RP,andBPP contain problems that, under diﬀerent

demands, can be considered eﬃciently solvable.

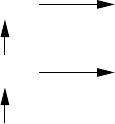
We obtain the following “complexity landscape” for algorithmic problems,

where the directed arrows represent subset relationships.

Theorem 3.3.8.

BPP PP

ZPP

∗

ZPP

Proof. The relationships P ⊆ ZPP, ZPP ⊆ ZPP

∗

,andBPP ⊆ PP follow directly

from the deﬁnitions of these classes.

By Theorem 3.3.2,

ZPP = ZPP(1/2) = ZPP(1/3) ⊆ BPP(1/3) = BPP ,

since “?” in a

BPP algorithm is an error. 

3.4 The Fundamental Complexity Classes for Decision Problems 35

One would like to show the corresponding relationship ZPP

∗

⊆ PP, but this

is presumably not true. A

ZPP algorithm with failure-probability 1 − 2

−2n

even if repeated independently 2

times would still with high probability

return “?” every time. We cannot return a correct result with an error-rate

less than 1/2.

When there are many possible results, “guessing the result” does not help.

This suggests special consideration of complexity classes for decision problems.

We have already seen (in Section 2.1) that optimization problems and evalua-

tion problems have obvious variants that are decision problems. In Chapter 4

we will see that these decision problems are complexity theoretically very sim-

ilar to their underlying optimization and evaluation problems. Therefore, we

will focus on decision problems in the next section.

3.4 The Fundamental Complexity Classes for Decision

Problems

The complexity classes P, ZPP, ZPP

∗

, BPP,andPP were deﬁned for algorithmic

problems. Since one-sided error only makes sense for decision problems,

and RP

∗

were only deﬁned for decision problems. If we focus on the class of

decision problems

DEC, then we have to consider the class P ∩ DEC instead of

P, and analogously for ZPP, ZPP

∗

, BPP,andPP. Of course, P ∩ DEC ⊆ RP, but

P ⊆ RP, since the former contains problems that are not decision problems.

But to the confusion of all who are introduced to complexity theory,

P, ZPP,

ZPP

∗

, BPP,andPP are used ambiguously to represent either the more general

classes or the classes restricted to decision problems. The hope is that from

context it will be clear if the class is restricted to decision problems. To avoid

using unusual notation, we will also use the ambiguous notation and do our

best to clarify any possible confusion. In this section in any case, we will

always restrict our attention to decision problems.

Associated to every decision problem, i.e., to every language, is its comple-

ment, which we will denote as

L or co-L. For complexity classes C,weletco-C

denote the class of all languages

co-L such that L ∈C. Since only classes with

one-sided error have asymmetric acceptance criteria, we have the following:

Remark 3.4.1. The complexity classes

P, ZPP, ZPP

∗

, BPP,andPP are closed

under complement. That is,

P = co-P, ZPP = co-ZPP, ZPP

∗

= co-ZPP

∗

, BPP =

co-BPP,andPP = co-PP.

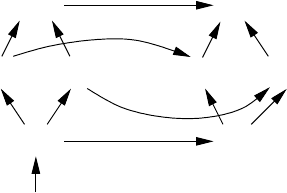
For decision problems there is a more complete complexity landscape than

for all algorithmic problems.

36 3 Fundamental Complexity Classes

Theorem 3.4.2.

BPP

co-RPRP

ZPP ZPP

∗

co-RP

∗

Proof. The inclusion P ⊆ ZPP and the “horizontal inclusions” between classes

of practially eﬃciently solvable problems (bounded error) and the correspond-

ing classes that do not give rise to practically useful algorithms, namely

ZPP ⊆ ZPP

∗

, RP ⊆ RP

∗

, co-RP ⊆ co-RP

∗

,andBPP ⊆ PP, follow directly

from the deﬁnitions.

ZPP ⊆ RP,andZPP

∗

⊆ RP

∗

, since the answer “?” for a failure can be

replaced by a rejection, possibly with error. Analogously,

co-ZPP ⊆ co-RP,

and since

ZPP = co-ZPP, ZPP ⊆ co-RP as well. Similarly, ZPP

∗

⊆ co-RP

∗

By Theorem 3.3.4,

RP = RP(1/2) = RP(1/3) ⊆ BPP(1/3) = BPP .

This is not surprising, since one-sided error is a stronger condition than two-

sided error. Analogously, we have

co-RP ⊆ co-BPP = BPP.

It remains to be shown that the inclusion

∗

⊆ PP holds, since co-RP

∗

⊆

co-PP = PP follows from this. For a decision problem L ∈ RP

∗

we investigate

∗

algorithm A and consider its worst-case runtime p(n), a polynomial

in the input length n. On an input of length n, the algorithm only has p(n)

random bits available. For each of the 2

p(n)

assignments of the random bits the

algorithm works deterministically. Thus we obtain a 0-1 vector A(x) of length

p(n)

that describes for each assignment of the random bits the decision of

the algorithm (1 = accept; 0 = reject). For the

RP algorithm A the following

hold:

• For x ∈ L, A(x)containsatleastone1.

• For x ∈ L, A(x)containsonly0’s.

We are looking for a

PP algorithm A



for L, that is, for an algorithm with

the following properties:

• For x ∈ L, A



(x) contains more 1’s than 0’s.

• For x ∈ L, A



(x) contains more 0’s than 1’s.

3.4 The Fundamental Complexity Classes for Decision Problems 37

The idea is to accept each input with a suitable probability and otherwise

to apply algorithm A. By doing this the acceptance probability is “shifted to

the right” – from 0 or at least 2

−p(n)

to something less than 1/2 or something

greater than 1/2, respectively. This “shifting of acceptance probability” can

be realized as follows: Algorithm A



uses 2p(n) + 1 random bits. The ﬁrst

p(n) + 1 random bits are interpreted as a binary number z.

• If 0 ≤ z ≤ 2

p(n)

(that is, in 2

p(n)

+1 of the 2

p(n)+1

cases), then we simulate

A using the remaining p(n) random bits.

• If 2

p(n)

<z≤ 2

p(n)+1

− 1 (that is, in the other 2

p(n)

− 1 cases) the input

is accepted without any further computation. Note that this happens for

p(n)

− 1) · 2

p(n)

of the 2

2p(n)+1

total assignments of the 2p(n) + 1 random

bits.

The analysis of the algorithm A



is now simple.

• If x ∈ L,thenA never accepts. So A



(x) contains only

p(n)

− 1) · 2

p(n)

2p(n)

− 2

p(n)

< 2

2p(n)+1

1’s, and therefore more 0’s than 1’s.

• If x ∈ L,thenA



(x) contains at most

p(n)

+1)· (2

p(n)

− 1) = 2

2p(n)

− 1 < 2

2p(n)+1

0’s, and therefore more 1’s than 0’s. 

The proof of the inclusion

∗

⊆ PP only appears technical. We have an

experiment that dependent on a property (namely, x ∈ L or x ∈ L)withprob-

ability ε

< 1/2orε

>ε

, respectively, produces an outcome E (accepting

input x). If we decide with probability p<1, to produce the outcome E in

any case, and with probability 1 − p to perform the experiment, then by the

Law of Total Probability (Theorem A.2.2) we have new probabilities



= p +(1− p)ε

= ε

+ p(1 − ε

)

and



= p +(1− p)ε

= ε

+ p(1 − ε

) >ε

+ p(1 − ε

)

for the outcome E. Now it only remains to choose p so that

+ p(1 − ε

) < 1/2 <ε

+ p(1 − ε

) .

Our work is only slightly more diﬃcult because in addition we must see to

it that p is of the form t/2

q(n)

for some polynomial q(n) so that the new

experiment can be realized in polynomial time.

To derive a relationship between

ZPP, RP,andco-RP, we can imagine the

associated algorithms as investment advisers. The

ZPP adviser gives advice in

at least half of the cases, and this advice is always correct, but the rest of the

38 3 Fundamental Complexity Classes

time he merely shrugs his shoulders. The RP adviser is very cautious. When

the prospects for an investment are poor, she advises against the investment,

and when the prospects are good, she only recommends the investment half of

the time. If she advises against an investment, we can’t be sure if she is doing

this because she knows the prospects are poor or because she is cautious. With

the

ZPP adviser, on the other hand, we always know whether he has given

good advice or is being cautious. With the

co-RP adviser the situation is like

that with the

RP adviser, only the tendencies are reversed. His advice is risky.

We won’t miss any good investments, but we are only warned about poor

investments at least half of the time. If we have both a conservative adviser

and an aggressive adviser, that is, both an

RP and a co-RP adviser, we should

be able to avoid mistakes. This is formalized in the following theorem.

Theorem 3.4.3.

ZPP = RP ∩ co-RP and ZPP

∗

= RP

∗

∩ co-RP

∗

Proof. We will only prove the ﬁrst equality. The proof is, however, correct

for all bounds ε(n), and so the second equality follows as well. The inclusion

ZPP ⊆ RP ∩ co-RP follows from Theorem 3.4.2, so we only need to show that

RP ∩ co-RP ⊆ ZPP.

If L ∈

RP ∩ co-RP, then there are polynomially bounded RP algorithms A

and

A for L and L, respectively. We run both algorithms, one after the other,

which clearly leads to a polynomially bounded randomized algorithm. Before

we describe how we will make our decision about whether x ∈ L, we will

investigate the behavior of the algorithm pair (A,

A).

• Suppose x ∈ L.Thensincex/∈

L, A rejects the input, which we will

denote by

A(x) = 0. Since x ∈ L, A accepts x with probability at least

1/2, which we denote with A(x)=1|0. So





is (1|0, 0).

• Suppose x/∈ L. Analogously,





is (0, 1|0).

The combined algorithm (A,

A) has three possible results (since (1, 1) is

impossible). These results are evaluated as follows:

• (1, 0): Since A(x)=1,x must be in L. (If x/∈ L,thenA(x) = 0.) So we

accept x.

• (0, 1): Since

A(x)=1,x must be in L. (If x ∈ L,thenA(x) = 0.) So we

reject x.

• (0, 0): One of the algorithms has clearly made an error, but we don’t know

which one, so we output “?”.

The new algorithm is error-free. If x ∈ L,then

A(x) = 0 with certainty,

and A(x) = 1 with probability at least 1/2, so the new algorithm accepts x

with probability at least 1/2. If x/∈ L, then it follows in an analogous way

that the new algorithm rejects with probability at least 1/2. All together, this

implies that the new algorithm is a

ZPP algorithm for L. 

3.5 Nondeterminism as a Special Case of Randomization 39

3.5 Nondeterminism as a Special Case of Randomization

Now that we have introduced important complexity classes using randomiza-

tion (which we consider as a key concept), we want to establish the connection

to the classical use of nondeterminism. Once again in this section we will only

consider decision problems.

With deterministic algorithms, the eﬀects of the next computation step

only depend on the information currently being read and the program instruc-

tion about to be executed. A randomized algorithm can at every step choose

between two actions based on the random bit available for that step, whereby

each action is performed with probability 1/2. A nondeterministic algorithm

can also choose at each step between two possible actions, but there are no

rules about how the choice between the two actions is to be made. Formally, a

nondeterministic Turing machine, just like a randomized Turing machine, has

a pair of programs (δ

,δ

) available to it. This is more typically, but equiv-

alently, described as a single function δ : Q × Γ → (Q × Γ ×{−1, 0, +1})

which contains both possible actions. An input is accepted if and only if there

is a legal computation path, i.e., a sequence of actions that agree with the

program, that leads to acceptance of the input.

Deﬁnition 3.5.1. A decision problem L belongs to the complexity class

(nondeterministic polynomial time) if there is a nondeterministic algorithm

with polynomially bounded worst-case runtime that accepts every x ∈ L along

at least one legal computation path, and rejects every x/∈ L along every legal

computation path.

This is the complexity class that was discussed in Chapter 1 in the con-

text of the

NP = P-hypothesis. It is admittedly diﬃcult to imagine the way

a nondeterministic machine works. The following explanations are frequently

used:

• Algorithmically, all computation paths are tried out. If the maximal run-

time is p(n), this can be as many as 2

p(n)

computation paths.

• The algorithm has the ability to “guess” the correct computation steps.

So we are dealing either with an exponentially long computation or with an

unrealizable concept. Thus nondeterministic computers are considered to be a

theoretically important but practically unrealizable concept. Randomization

provides simpler access to the class

NP.

Theorem 3.5.2.

NP = RP

∗

Proof. The deﬁnitions of

NP and RP

∗

expect algorithms with polynomially

bounded worst-case computation time p(n) and two possible actions in each

situation. For x/∈ L,an

NP algorithm must reject along every computation

path, and for an

∗

algorithm this must happen with probability 1. Since

every computation path has a probability of at least 2

−p(n)

, the two require-

ments are equivalent. For x ∈ L,an

NP algorithm must accept x along at least

40 3 Fundamental Complexity Classes

one computation path, and an RP

∗

algorithm must reject with a probability

less than 1. Once again, these two statements are equivalent. 

∗

algorithm, and therefore an NP algorithm, can be performed on a

randomized computer with polynomially bounded computation time, and is

therefore a realizable algorithmic concept. It just isn’t practically useful due

to the potentially large error-probability.

Nondeterminism is the same thing as randomization where one-sided

errors and any error-probability less than 1 are allowed.

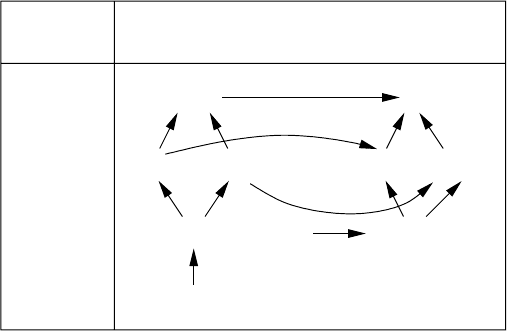
Now we can insert the results of Theorem 3.4.3 into Theorem 3.4.2 and

reformulate Theorem 3.4.2 with the usual notation.

Theorem 3.5.3.

BPP

co-RPRP

NP co-NP

∩ co-NPZPP = RP ∩ co-RP

error

two-sided

one-sided

error

failure-probability

bounded error or unbounded error or

failure-probability

zero error

but failure

no error

no failure



The rows and columns in the ﬁgure above reﬂect the characterization from

the modern perspective with the focus on randomization. The terminology of

the complexity classes arose historically, and are rather unfortunately chosen.

For example,

BPP (B = bounded) is not the only class for which the diﬀer-

ence between the trivial error-probability and the tolerated error-probability

is bounded by a constant; the same is true for

RP algorithms and for the

failure-probability of

ZPP algorithms. In ZPP and BPP, the second P stands

for probabilistic, and in

RP,theR stands for random, although randomization

is involved in all these classes. The classes

PP and NP deal with randomized

algorithms with unacceptable error-probabilities, but only

PP indicates this

in its name. Finally, the class

NP ∩ co-NP, in contrast to ZPP = RP ∩ co-RP,

hasnorealnameofitsown.

When the complexity class

NP was “discovered” (in the 1960’s), random-

ized algorithms were exotic outsiders, while formal languages had been highly

developed as the basis for programming languages. A word belongs to the