Wegener I. Complexity Theory. Exploring the Limits of Efficient Algorithms

Подождите немного. Документ загружается.

240 15 Communication Complexity

such a way that distinct inputs a and a



have only few ﬁngerprints in common.

So for a random choice of ﬁngerprint, Bob can check the property “a = b”

with small error-probability.

Theorem 15.4.3. R

1,1/n

(

)=O(log n).

Proof. Alice and Bob interpret their inputs as binary numbers a, b∈

{0,...,2

− 1}. Both of them compute the n

smallest prime numbers. From

number theory we know that the size of these prime numbers is O(n

log n)

and so each of these primes can be described with O(log n) bits. Alice ran-

domly selects one of these prime numbers, and sends to Bob the type of ﬁn-

gerprint (p) and the ﬁngerprint itself, namely a mod p. Bob checks whether

a≡b mod p, and sends the result of this test back to Alice. The input is

rejected if a≡b mod p. The length of this protocol is Θ(log n) and inputs

(a, b)witha = b are always rejected. We need to approximate the probability

that an input (a, b) is accepted if a = b. If there are k primes among the small-

est n

primes for which a≡b mod p, then this probability is k/n

. We will

show that there are fewer than n primes p such that a≡b mod p, i.e., that

k<n. For this we need a simple result from elementary number theory. If

a≡b mod m

and a≡b mod m

for two relatively prime numbers m

and m

,thena≡b mod m

as well. The assumptions say that a−b

is an integer multiple of m

and an integer multiple of m

.Sincem

and m

are relatively prime, a−b must then be an integer multiple of m

.If

a≡b mod p for n prime numbers p, then this will also be true for their

product. But since each of these primes is at least 2, their product must be

greater than 2

.Butifa≡b mod N for an integer N with N ≥ 2

,then

a = b,soa = b. Thus the error-probability is bounded by n/n

=1/n.



When we deﬁned randomized communication protocols in Section 15.3 we

emphasized that Alice knows r

but not r

and that Bob knows r

but not

. What diﬀerence does it make if we have only one random vector of length

+ l

which is known to both Alice and Bob? To distinguish between these

two models, we will say that our original model uses private coins,andthat

the modiﬁed model uses public coins. We will use a superscripted “pub” in

our notation to distinguish the public-coin complexity measures from their

private-coin counterparts. Clearly Theorem 15.4.1 is still valid for protocols

with public coins. Furthermore,

Remark 15.4.4. A protocol with private coins can be simulated by a protocol

with public coins. So for example, R

pub

2,ε

(f) ≤ R

2,ε

(f).

Proof. Let l

and l

be the lengths of the random vectors for Alice and Bob

in a protocol with private coins. The protocol with public coins uses a random

vector of length l

+ l

. During the simulation, Alice uses the preﬁx of the

random vector of length l

, and Bob uses the suﬃx of length l

. 

15.4 Randomized Communication Protocols 241

Public coins sometimes lead to short and elegant protocols, as the following

result shows.

Theorem 15.4.5. R

pub

1,1/2

(

) ≤ 2.

Proof. Alice and Bob use a public random vector r ∈{0, 1}

. Alice computes

the Z

-sum of all a

with 1 ≤ i ≤ n and sends the result h

(a) to Bob.

The notation h

should remind us of the hash function used in the proof

of Theorem 11.3.4. Bob computes h

(b) and sends the result to Alice. They

accept the input if h

(a) = h

(b). The length of the protocol is 2. If a = b,

then h

(a)=h

(b) for all r and the protocol works without error. If a = b,

then there is a position i with a

= b

. By symmetry it suﬃces to consider the

case that a

= 0 and b

=1.Leth

∗

(a)betheZ

-sum of all a

with j = i;

∗

(b) is deﬁned analogously. Then h

(a)=h

∗

(a)andh

(b)=h

∗

(b) ⊕ r

.So

the probability that h

(a)=h

(b) is exactly 1/2 and so the error-rate is 1/2.



Is it possible for R

1,ε

(f)andR

pub

1,ε

(f)orR

2,ε

(f)andR

pub

2,ε

(f)todiﬀer

even more strongly? It can be shown that R

1,1/4

(

) ≥ R

2,1/4

(EQ

Ω(log n). On the other hand, by Theorems 15.4.5 and 15.4.1 it follows that

pub

1,1/4

(

) ≤ 4. Thus we already have an example where the diﬀerence

between the two models is essentially as large as possible.

Theorem 15.4.6. Let f : {0, 1}

×{0, 1}

→{0, 1} and δ>0 be given. Then

• R

2,ε+δ

(f) ≤ R

pub

2,ε

(f)+O(log n +logδ

−1

),and

• R

1,ε+δ

(f) ≤ R

pub

1,ε

(f)+O(log n +logδ

−1

Proof. In this proof we use the fact that communication protocols are a non-

uniform model. The protocols generated here are not in general eﬃciently

computable. In this aspect and in the methodology we orient ourselves on

the proof that

BPP ⊆ P/poly (Theorem 14.5.1, Corollary 14.6.3). In that case

there was a single golden computation path. Here we will show that there

are t = O(n · δ

−2

) computation paths such that the random choice of one of

these computation paths only lets the error-probability grow from ε to ε + δ.

From this the claims of the theorem follow easily. Alice and Bob agree on the

good computation paths, and Alice generates with her private random bits a

random i ∈{1,...,t} and sends i to Bob using O(log t)=O(log n +logδ

−1

)

bits. Then Alice and Bob simulate the ith of the selected computation paths.

Suppose we have an optimal randomized communication protocol with a

public random vector r of length l. The two cases, namely one-sided error and

two-sided error, are handled with the same argument. Let Z(a, b, r

∗

)=1if

the given protocol on input (a, b)withr = r

∗

provides an incorrect result, and

let Z(a, b, r

∗

) = 0 otherwise. We can imagine the Z-values as a matrix, the

rows of which represent the inputs (a, b) and the columns the vectors r

∗

.By

assumption, the proportion of 1’s in each row is bounded by ε (for one-sided

242 15 Communication Complexity

error the rows contain no 1’s for (a, b) ∈ f

−1

(0)). We want to show that there

is a selection of t columns such that each row of the submatrix restricted to

these columns has a proportion of at most ε + δ 1’s (for one-sided error, of

course, the shortened rows contain no 1’s for (a, b) ∈ f

−1

(0)). With these t

random vectors – or, equivalently, with these t computation paths – we can

complete the argument we began above. To be precise we must mention that

columns may be chosen more than once.

We prove the existence of t such columns using the probabilistic method

(see Alon and Spencer (1992)). This method proves the existence of an object

with certain properties by designing a suitable random experiment and show-

ing that the probability that the result of this experiment is an object with

the desired properties is positive. The potential of this method was ﬁrst rec-

ognized and employed by Erd˝os. In our case, we randomly and independently

select t computation paths r

,...,r

.LetR be the random variable that takes

on the values r

,...,r

each with probability 1/t.Bydeﬁnition

E(Z(a, b, R)) =



1≤i≤t

Z(a, b, r

)/t .

But since r

,...,r

are also randomly selected, we can use the Chernoﬀ In-

equality to prove that

Prob





1≤i≤t

Z(a, b, r

)/t ≥ ε + δ



≤ 2e

−δ

In Theorem A.2.11 we proved a form of the Chernoﬀ Inequality in which

Prob(X ≤ (1 − δ) · E(X)) is bounded from above. Here we require a Chernoﬀ

Inequality for estimating Prob(X ≥ (1+δ)·E(X)) (see Motwani and Raghavan

(1995)). If t =2nδ

−2

+1, then 2e

−δ

< 2

−2n

. Since there are only 2

inputs

(a, b), the probability that



1≤i≤t

Z(a, b, r

)/t ≥ ε + δ

is smaller than 1 for any input (a, b). So the probability of a selection of

,...,r

such that the error-probability for each input is bounded by ε + δ

is positive, and so t suitable vectors r

,...,r

must exist. This completes the

proof. 

For a constant ε<1/2 in the case of two-sided error (or ε<1 in the case of

one-sided error) we can choose a constant δ>0 such that ε+δ<1/2(ε+δ<1

in the case of one-sided error). By Theorem 15.4.1 and Theorem 15.4.6 it

follows that

2,ε

(f)=O(R

pub

2,ε

(f)+logn)

and

1,ε

(f)=O(R

pub

1,ε

(f)+logn) .

15.4 Randomized Communication Protocols 243

These results demonstrate a certain robustness of our model of randomized

communication protocols with private coins. We have also already encoun-

tered a method for designing short randomized communication protocols.

Lower bounds for one-sided error follow from lower bounds for nondetermin-

istic communication protocols. But what is the situation for randomized com-

munication protocols with two-sided error? As in Section 9.2 we will make use

of the theory of two-person zero-sum games to characterize R

pub

2,ε

(f)usinga

measure for deterministic protocols and randomly selected inputs.

For f : A × B → C we consider probability distributions p on A × B

and investigate deterministic protocols such that the error-probability with

respect to p is bounded by ε.WeletD

p,ε

(f) denote the length of the shortest

deterministic protocol that for a p-random choice of input yields an error-

probability bounded by ε. The corresponding complexity measure is called

(p, ε)-distributional communication complexity, but it is clearer to speak of

this as the complexity of ε-approximations for f with respect to p.

Theorem 15.4.7. For any function f : A × B → C and each δ>0,

• R

pub

2,ε

(f) ≥ max{D

p,ε

(f) | p a distribution on A × B},and

• R

pub

2,ε+δ

(f) ≤ max{D

p,ε

(f) | p a distribution on A × B}.

Proof. For the proof of the lower bound we assume there is a randomized

communication protocol of length R

pub

2,ε

(f) with an error-probability of ε.The

error-bound is valid for every input (a, b), and thus also for any input randomly

selected according to the distribution p and A×B. If the randomized protocol

uses a random vector r of length l, then we are dealing with a random choice

from among 2

deterministic protocols. If all of these protocols had an error-

probability greater than ε with respect to p, then the randomized protocol

would also have an error-probability greater than ε, which would contradict

the assumption. Therefore there must be a deterministic protocol with length

pub

2,ε

(f) that has an error-probability bounded by ε with respect to p-random

inputs.

For the proof of the other inequality we investigate the following two-

person zero-sum game. For d := max

p,ε

(f)}, Alice can select a determin-

istic communication protocol P of length d and Bob gets to choose the input

(a, b). The payoﬀ matrix M has a 1 in position ((a, b),P) if the protocol P

makes an error on input (a, b), otherwise this position contains a 0. Recall

that Alice must pay this amount to Bob. By the deﬁnition of d, against each

randomized strategy of Bob (that is, for each probability distribution p on

A × B), Alice has a deterministic strategy (that is, a deterministic commu-

nication protocol) for which her expected payout is bounded by ε.Sothe

value of the game is bounded by ε. By the Minimax Theorem (see Owen

(1995)) it follows that there is a randomized strategy for Alice (i.e., a prob-

ability distribution over the protocols of length at most d)thatguarantees

for each input (a, b) an error-probability of at most ε. For Alice and Bob to

produce a common communication protocol from this, they must be able to

244 15 Communication Complexity

make the corresponding random decision. This is possible using a common

random vector, i.e., with public coins. To be precise, Alice and Bob would

need an inﬁnite sequence of random bits to correctly realize probabilities like,

for example, 1/3. But with ﬁnitely many random bits they can approximate

any error-probability ε arbitrarily accurately. 

We can omit the additive term δ for the error-probability if we allow the

individual random bits to take on the value 1 with a probability that is not

necessarily 1/2 but is instead p

for the ith random bit. We won’t pursue

this idea further here since we are primarily interested in the “≥” part of

Theorem 15.4.7. In order to prove lower bounds for R

pub

2,ε

(f)wecanchoose

a distribution p on A × B and prove a lower bound for D

p,ε

(f). This is one

form of Yao’s minimax principle.

Now, of course, we have the diﬃculty of proving lower bounds for D

p,ε

(f).

Since we are once again dealing with deterministic protocols, we can hope to

make use of our techniques involving sizes of rectangles with various proper-

ties. Since we may make errors on some of the inputs, the rectangles describ-

ing the inputs that lead to a leaf v may not be monochromatic. But if the

error-probability is small, then these rectangles will either be small or almost

monochromatic with respect to p.Forf : A × B →{0, 1}, a probability dis-

tribution p on A × B, and a rectangle R ⊆ A × B,letR

:= f

−1

(0) ∩ R and

:= f

−1

(1) ∩ R, and let the discrepancy of R with respect to f and p be

deﬁned by

Disc

p,f

(R):=|p(R

) − p(R

)| .

It follows that Disc

p,f

(R) ≤ p(R) and that small rectangles cannot have large

discrepancy. Finally, let

Disc

(f):=max{Disc

p,f

(R) | R ⊆ A × B and R is a rectangle}

be the discrepancy of f with respect to p. The following result shows that a

small discrepancy implies a large communication complexity with respect to

the distribution, and thus a large communication complexity with respect to

randomized protocols with two-sided error.

Theorem 15.4.8. If f is a function f : A × B →{0, 1}, p a probability

distribution on A × B,and0 <ε≤ 1/2, then

p,1/2−ε

(f) ≥ log(2ε) − log(Disc

(f)) .

Proof. This result follows directly from the deﬁnitions and a simple calcula-

tion. We consider a deterministic protocol of length d := D

p,1/2−ε

(f)with

an error-probability of at most 1/2 − ε with respect to p. The corresponding

protocol tree has at most 2

leaves v ∈ L at which precisely the inputs in the

rectangle R

⊆ A × B arrive. The rectangles R

for v ∈ L form a partition

of A × B.LetE

denote the set of all inputs on which the protocol works

correctly, and let E

−

:= (A × B) − E

be the set of all inputs on which

15.4 Randomized Communication Protocols 245

the protocol makes an error. By our assumption, p(E

−

) ≤ 1/2 − ε and so

p(E

) ≥ 1/2+ε. It follows that

2ε ≤ p(E

) − p(E

−

)



v∈L



p(E

∩ R

) − p(E

−

∩ R

)



≤



v∈L

|p(E

∩ R

) − p(E

−

∩ R



v∈L

Disc

p,f

)

≤ 2

Disc

(f).

Here we are only using the deﬁnitions of Disc

p,f

(R)andDisc

(f). We obtain

the claim of the theorem by solving this inequality for d := D

p,1/2−ε

(f). 

It is not always easy to apply this method. As an example we will inves-

tigate IP

Theorem 15.4.9. If 0 <ε≤ 1/2, then

pub

2,1/2−ε

(IP

) ≥ n/2+logε.

Proof. By Theorem 15.4.7 and Theorem 15.4.8 it suﬃces to prove for some

distribution p on {0, 1}

×{0, 1}

an upper bound of 2

−n/2

for the discrepancy

of arbitrary rectangles A × B. We will use the uniform distribution u on

{0, 1}

×{0, 1}

. In addition, we will replace the 1’s in the communication

matrix with −1’s and the 0’s with 1’s. The result is the Hadamard matrix H

introduced in Section 15.2. This has the advantage that we can now compute

the discrepancy (now with respect to the colors 1 and −1) algebraically. By

deﬁnition

Disc

u,IP

(A × B)=



#{(a, b) ∈ A × B | H

(a, b)=1}−

#{(a, b) ∈ A × B | H

(a, b)=−1}





(a,b)∈A×B

(a, b)



Let e

∈{0, 1}

be the characteristic vector of A ⊆{0, 1}

,andlete

the characteristic vector of B ⊆{0, 1}

.Thene



· H

· e

sums exactly those

(a, b)with(a, b) ∈ A × B.Thus

Disc

u,IP

(A × B)=|e



· H

· e

|/2

246 15 Communication Complexity

and it is suﬃcient to demonstrate an upper bound of 2

3n/2

for |e



·H

·e

|.For

this we can make use of the algebraic properties of H

.Forthe2

×2

-identity

matrix I

it follows by simple computation that

· H



· I

The matrix H

· H



has in position (a, b)theentry



c∈{0,1}

(a, c) · H

(b, c) .

If a = b,thenH

(a, c)=H

(b, c) ∈{−1, +1}, H

(a, c) · H

(b, c)=1and

the sum is 2

. As in the proof of Theorem 15.4.5, if a = b,thenIP

(a, c)=

(b, c) for exactly half of all c ∈{0, 1}

.SohalfofallH

(a, c) · H

(b, c)

have the value 1, and the other half have the value −1. Thus the sum of these

values is 0. Since I

has only one eigenvalue, namely 1, the only eigenvalue of

· H



· I

is 2

. From this it follows that the spectral norm ||H

of H

has the value 2

n/2

. The norm of vectors is their Euclidean length.

Thus ||e

= |A|

1/2

≤ 2

n/2

and ||e

≤ 2

n/2

. These norms measure how

much vectors are lengthened when multiplied by the vector or matrix being

investigated. Thus



· H

· e

|≤||e

·||H

·||e

≤ 2

3n/2

and Disc

u,IP

(A × B) ≤ 2

−n/2

for arbitrary rectangles A × B. 

Randomized communication protocols, even with very small error-

probabilities, can be exponentially shorter than deterministic commu-

nication protocols. It doesn’t make much diﬀerence if the random bits

are public or private. If with respect to some probability distribution

on the inputs every rectangle of the communication matrix contains

roughly half 0’s and half 1’s, then the randomized communication com-

plexity of the corresponding function is large.

15.5 Communication Complexity and VLSI Circuits

We will be satisﬁed with a naive understanding of VLSI circuits based on

the simple model described below. The lower bounds we obtain for this sim-

ple model will certainly hold for any more realistically restricted model. We

imagine a VLSI circuit as a rectangular grid of length l and width w.Thegrid

has area A := lw and consists of lw cells. Each cell can hold at most one bit

of the input and is potentially connected only to the (at most four) cells with

whichitsharesacellwall.Ineachtimeunitatmostonebitcanbesentin

one direction across each connection. For functions with one output y there is

a cell that contains this result at the end of the computation. A VLSI circuit

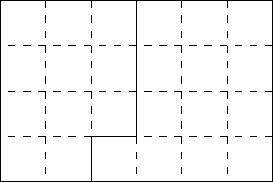
with eight inputs and one output is shown in Figure 15.5.1.

15.6 Communication Complexity and Computation Time 247

Fig. 15.5.1. A VLSI circuit of width 6 and length 4.

We can see from this diagram that it will always be possible to cut the

circuit so that n/2 inputs are on one side of the cut and n/2 inputs are

on the other side and such that the cut consists of at most l + 1 cell walls.

By symmetry we can assume that l ≤ w and thus that l ≤ A

1/2

. In each time

unit, at most l + 1 bits can be communicated across this cut. If we partition

the input bits in such a way that Alice receives the bits on one side of the

cut and Bob the bits on the other side, then we can establish a connection

among the communication complexity of f with respect to this partition of

the input bits, the area A, and the parallel computation time T of the VLSI

circuit, namely

C(f) ≤ (A

1/2

+1)· T +1.

ThisisbecauseineachoftheT time steps at most A

1/2

+ 1 bits can be

sent across the cut. This can be simulated by a deterministic communication

protocol. The extra summand +1 is necessary, since in the VLSI circuit only

one cell, i.e., only Alice or only Bob, must know the result. In a communication

protocol this result must be communicated. Since the complexity of VLSI

circuits is usually measured in terms of AT

, our result can be expressed as

= Ω(C(f)

As we see, we cannot partition the input arbitrarily. For the middle bit

of multiplication (MUL), however, we have proven a linear lower bound for

the communication complexity that is valid for any partition of the input bits

that gives half of the bits of the ﬁrst factor to each of Alice and Bob. If we

modify our cut in the VLSI circuit so that it only takes into consideration

the bits of the ﬁrst factor, then we can still apply the observations above to

obtain the following result:

Theorem 15.5.1. For VLSI circuits that compute the middle bit of multipli-

cation for two factors of length n, AT

= Ω(n

). 

15.6 Communication Complexity and the Computation

Time of Turing Machines

Turing machines with k tapes and runtime t(n) can be simulated by Turing

machines with one tape and runtime O(t(n)

). Is this quadratic slowdown

248 15 Communication Complexity

necessary? At least for linear runtimes we can answer these questions by giving

a language that can be decided in linear time by a Turing machine with two

tapes but requires quadratic time for any Turing machine with only one tape.

For f =(f

)withf

: {0, 1}

×{0, 1}

→{0, 1} let

∗

= {acb : |a| = |c| = |b|,a,b∈{0, 1}

∗

,c∈{2}

∗

|a|

(a, b)=1} .

Remark 15.6.1. The language L

∗

can be decided by a two-tape Turing ma-

chine in time O(n).

Proof. In one pass over the input tape we can test whether the input has the

form acb with a, b ∈{0, 1}

∗

and c ∈{2}

∗

, and simultaneously copy b to the

second tape. By reading a and b at the same time, we can test whether they

have the same length, and if so, we can compute EQ

(a, b). Finally, we can

check whether b and c have the same length. 

More interesting than this simple observation is the proof of a lower bound

for the runtime of Turing machines with only one tape.

Theorem 15.6.2. If the language L

∗

for f =(f

) is decided by a one-tape

Turing machine M in time t(n), then

pub

)=O(t(3n)/n +1).

Proof. We want to design a randomized, error-free communication protocol for

that has a small expected length for every input. Alice knows a ∈{0, 1}

and Bob knows b ∈{0, 1}

. In particular, each of them knows n and the

way M works on the input w = a2

b,where2

denotes a sequence of n 2’s.

With the help of the publicly known random vector, Alice and Bob select a

random i ∈{0,...,n}. This is used to divide the tape of M between Alice

and Bob. Alice receives the left portion, up to cell n + i, and Bob receives the

rest. Since the head of M is reading a

at the beginning of the computation,

Alice can simulate the ﬁrst portion of the computation. When M crosses over

the dividing line from left to right, Alice sends Bob the state of the Turing

machine. This requires only log |Q| = O(1) bits. Now Bob can simulate the

Turing machine until the dividing line is crossed from right to left and send

Alice the state of the Turing machine at that point. This process continues

until the machine halts. At that point, one of Alice and Bob knows the result

and communicates it to the other. This protocol is error-free since M is error-

free and correctly simulated.

Now let z

= z

(a, b) be the number of computation steps at which the

dividing line between tape cells n + i and n + i + 1 is crossed. Since at each

step at most one dividing line can be crossed and |w| =3n it follows that

+ ···+ z

≤ t(3n)

and

15.6 Communication Complexity and Computation Time 249

+ ···+ z

)/(n +1)≤ t(3n)/n .

So on average, Alice and Bob send at most t(3n)/n messages of length O(1)

and at the end one additional message of length 1. This proves the theorem.



By Theorem 15.3.5 C

(EQ

) ≥ n, and thus R

1,2/3

(EQ

) ≥ n.Soby

Theorem 15.4.6 R

pub

1,1/2

(EQ

)=Ω(n). By the variant of Theorem 15.4.1 for

protocols with public coins, it follows that R

pub

(EQ

)=Ω(n). Finally, using

Theorem 15.6.2 we obtain the desired result:

Theorem 15.6.3. For one-tape Turing machines that decide L

∗

in time

t(n), t(n)=Ω(n

). 

The results of the last two sections show that results about the com-

munication complexity of speciﬁc problems can support the solution of

problems from very diﬀerent areas.