Воробей В.В., Маркин В.Б. Основы технологии и проектирования корпусов ракетных двигателей
Подождите немного. Документ загружается.


Ãëàâà 6
Ðàñ÷åò è ïðîåêòèðîâàíèå
âíóòðåííåé òåïëîçàùèòû êîðïóñà
6.1. Àëãîðèòì ðàñ÷åòà òðåáóåìûõ òîëùèí
òåïëîçàùèòíîãî ïîêðûòèÿ
Òðåáóåìûå òîëùèíû ïîêðûòèÿ (ñ ãåðìîñëîåì è àíòèäèôôóçè
-
îííûì ñëîåì) îïðåäåëÿþòñÿ èç óñëîâèÿ íåïðåâûøåíèÿ ñ çàäàííîé
íàäåæíîñòüþ â òå÷åíèå çàäàííîãî âðåìåíè òåìïåðàòóðîé çàùèùàå
-
ìîé ïîâåðõíîñòè ñèëîâîé îáîëî÷êè äîïóñêàåìîãî çíà÷åíèÿ.
Äëÿ ñå÷åíèé, ðàñïîëîæåííûõ âíå çîí ïîâûøåííûõ îòíîñèòåëü
-
íûõ äåôîðìàöèé ïîêðûòèÿ
*
, ðàñ÷åò òðåáóåìûõ òîëùèí ïîêðûòèÿ
ïðîèçâîäèòñÿ ïî ôîðìóëå
[]
ddd
ÒÇÏ ç â ïð â
=+kk t t
gd
() (),
(6.1)
ãäå
k
g
— ýìïèðè÷åñêèé êîýôôèöèåíò âëèÿíèÿ èíåðöèîííûõ ïåðå-
ãðóçîê íà ãëóáèíó äåñòðóêöèè ïîêðûòèÿ;
d
d
— ãëóáèíà äåñòðóêöèè;
d
ïð
— òîëùèíà ñëîÿ ïîêðûòèÿ, ïðîãðåòîãî äî äîïóñêàåìîé íà åãî
âíóòðåííåé ïîâåðõíîñòè òåìïåðàòóðû;
t
â
— ïðîäîëæèòåëüíîñòü âîç-
äåéñòâèÿ ïðîäóêòîâ ñãîðàíèÿ íà ïîâåðõíîñòü ïîêðûòèÿ â ðàñ÷åòíîì
ñå÷åíèè; k
ç
— êîýôôèöèåíò çàïàñà òîëùèí ïîêðûòèÿ (êîýôôèöèåíò
áåçîïàñíîñòè).
Êîýôôèöèåíò âëèÿíèÿ ïåðåãðóçîê íà ãëóáèíó äåñòðóêöèè ïî
-
êðûòèÿ îïðåäåëÿåòñÿ ýêñïåðèìåíòàëüíî ïî ñïåöèàëüíîé ìåòîäèêå
íà ãàçîãåíåðàòîðàõ, óñòàíîâëåííûõ íà öåíòðèôóãå.
Ãëóáèíà äåñòðóêöèè ïîêðûòèÿ ðàññ÷èòûâàåòñÿ äâóìÿ ñïîñîáàìè:
— íà îñíîâå ÷èñëåííîãî ðåøåíèÿ êðàåâîé çàäà÷è íåñòàöèîíàð
-
íîé òåïëîïðîâîäíîñòè â ïîêðûòèè è ñòåíêå êîðïóñà ñ ó÷åòîì â ÿâ
-
íîé ôîðìå ïîâåðõíîñòíîãî è âíóòðåííåãî óíîñà ìàññû;
— ñ èñïîëüçîâàíèåì ýìïèðè÷åñêîãî êîýôôèöèåíòà äåñòðóêöèè
ïîêðûòèÿ, ó÷èòûâàþùåãî â íåÿâíîé ôîðìå ïîâåðõíîñòíûé è âíóò
-
ðåííèé óíîñ ìàññû.
Âî âòîðîì ñëó÷àå äëÿ ðàñ÷åòà ãëóáèíû äåñòðóêöèè ïîêðûòèÿ èñ
-
ïîëüçóåòñÿ ôîðìóëà âèäà
dx
dd
tt=−()
ê
ïðè
tt≥
ê
, (6.2)
Ðàñ÷åò è ïðîåêòèðîâàíèå âíóòðåííåé òåïëîçàùèòû êîðïóñà 101
* Çîíû ïîâûøåííûõ äåôîðìàöèé ïîêðûòèÿ ðàñïîëîæåíû â ìåñòàõ ñîåäèíåíèÿ
ïëàñòèêîâîé îáîëî÷êè êîðïóñà.

ãäå
x
d
— êîýôôèöèåíò äåñòðóêöèè ïîêðûòèÿ;
t
— òåêóùåå çíà÷åíèå
âðåìåíè;
t
ê
— âðåìÿ ïðîãðåâà ïîâåðõíîñòè ïîêðûòèÿ äî òåìïåðàòó
-
ðû êîêñîâàíèÿ.
Ëèíåéíàÿ ñêîðîñòü óíîñà ìàññû ïîêðûòèÿ ñóáëèìèðóþùåãî
òèïà îïðåäåëÿåòñÿ ïî ôîðìóëå
v
q
H
=
r
, (6.3)
ãäå q — ïëîòíîñòü òåïëîâîãî ïîòîêà, ïîñòóïàþùåãî ê ïîâåðõíîñòè
ïîêðûòèÿ;
r
— ïëîòíîñòü ìàòåðèàëà ïîêðûòèÿ; Í— ýôôåêòèâíàÿ
ýíòàëüïèÿ ïîêðûòèÿ.
Òîëùèíà ïðîãðåòîãî ñëîÿ ïîêðûòèÿ âî âñåõ ñëó÷àÿõ ðàññ÷èòûâà
-
åòñÿ ïóòåì ÷èñëåííîãî ðåøåíèÿ óðàâíåíèÿ íåñòàöèîíàðíîé òåïëî
-
ïðîâîäíîñòè â ñòåíêå êîðïóñà.
Äëÿ ðàñ÷åòíûõ ñå÷åíèé, ðàñïîëîæåííûõ â çîíàõ ïîâûøåííûõ
îòíîñèòåëüíûõ äåôîðìàöèé ïîêðûòèÿ, ôîðìóëà äëÿ ðàñ÷åòà åãî òðå-
áóåìûõ òîëùèí èìååò âèä
dd e
ÒÇÏ
ÒÇÏ
=+
∂
/( ),1
y
(6.4)
ãäå
e
y
— ïîïåðå÷íàÿ äåôîðìàöèÿ ïîêðûòèÿ.
Ïîïåðå÷íàÿ äåôîðìàöèÿ ïîêðûòèÿ îïðåäåëÿåòñÿ èç ñîîòíîøåíèÿ
eee
yxz
=− − ,
(6.5)
ãäå
ee
xz
,
— ìåðèäèîíàëüíàÿ è îêðóæíàÿ äåôîðìàöèè ïîêðûòèÿ.
Ñîîòíîøåíèå (6.5) ïîëó÷åíî ïðè çíà÷åíèè êîýôôèöèåíòà Ïóàñ-
ñîíà ìàòåðèàëà ïîêðûòèÿ, ðàâíîì 0,5. Âõîäÿùèå â íåãî ìåðèäèîíàëü
-
íàÿ è îêðóæíàÿ äåôîðìàöèè ïîêðûòèÿ îïðåäåëÿþòñÿ èç ðàñ÷åòà íàïðÿ
-
æåííî-äåôîðìèðîâàííîãî ñîñòîÿíèÿ ñèñòåìû ïëàñòèêîâàÿ îáîëî÷
-
êà — ìåòàëëè÷åñêèé ôëàíåö — ïîêðûòèå. Íàïðèìåð, ïðè
e
x
= 025,,
e
z
= 002,
ïîëó÷àåì
e
y
= 027,.
Òîãäà
dd
¶
ïîêð ïîêð
= 1345,
.
Ïðè ðàñ÷åòàõ òîëùèíû ïðîãðåòîãî ñëîÿ äåôîðìèðîâàííîãî ïî
-
êðûòèÿ èñïîëüçóþòñÿ òåïëîôèçè÷åñêèå õàðàêòåðèñòèêè, îïðåäåëåí
-
íûå ñ ó÷åòîì âëèÿíèÿ íà íèõ äåôîðìàöèè.
Ïðè ðàñ÷åòàõ òîëùèíû ïîêðûòèÿ â çîíàõ ðàñêðåïëåíèÿ ñèñòåìû
íàïîëíèòåëü — êîðïóñ (çàìàíæåòíûõ ïîëîñòÿõ) ó÷èòûâàåòñÿ âîç
-
ìîæíîå âëèÿíèå àãëîìåðàòîâ êîíäåíñèðîâàííîé ôàçû, âûïàäàþùèõ
â çàìàíæåòíóþ ïîëîñòü.
Çíà÷åíèå êîýôôèöèåíòà çàïàñà òîëùèí ïîêðûòèÿ îïðåäåëÿåòñÿ â
ïðåäïîëîæåíèè î íîðìàëüíîì çàêîíå ðàñïðåäåëåíèÿ ýòîé ñëó÷àéíîé
âåëè÷èíû, ïîëó÷åííîì ñòàòèñòè÷åñêîé îáðàáîòêîé ðåçóëüòàòîâ èçìå
-
ðåíèé òîëùèí ïîêðûòèÿ ðÿäà èçäåëèé-ïðîòîòèïîâ. Äëÿ ðàñ÷åòà êî
-
ýôôèöèåíòà çàïàñà èñïîëüçóþòñÿ ðåçóëüòàòû ñòàòèñòè÷åñêîãî àíàëèçà
102 Ãëàâà 6

ýêñïåðèìåíòàëüíûõ äàííûõ, ïîëó÷åííûõ ñ èñïîëüçîâàíèåì ïëàíèðî
-
âàíèÿ ýêñïåðèìåíòà. Ïðè ýòîì ó÷èòûâàåòñÿ âëèÿíèå òàêèõ ôàêòîðîâ,
êàê:
— ñîäåðæàíèå êîìïîíåíòîâ â ìàòåðèàëå;
— íåîäíîðîäíîñòü åãî ñòðóêòóðû;
— ðåæèìû òåðìîîáðàáîòêè ïîêðûòèÿ, êîðïóñà, èçäåëèÿ â öåëîì.
Êîýôôèöèåíò çàïàñà òîëùèí ïîêðûòèÿ îïðåäåëÿåòñÿ ñîîòíîøå
-
íèåì
k
ç
íîì
=+1
Dd
d
,
(6.6)
ãäå
Dd
— ðàçáðîñ òîëùèí ïîêðûòèÿ ïðè çàäàííîé âåðîÿòíîñòè åãî
áåçîòêàçíîé ðàáîòû;
d
íîì
— òðåáóåìàÿ òîëùèíà ïîêðûòèÿ, îïðåäå
-
ëåííàÿ ïðè íîìèíàëüíûõ çíà÷åíèÿõ åãî õàðàêòåðèñòèê.
Ïîñêîëüêó òîëùèíà ïîêðûòèÿ ÿâëÿåòñÿ ñëó÷àéíîé âåëè÷èíîé è
çàâèñèò îò áîëüøîãî ÷èñëà ïåðâè÷íî íåçàâèñèìûõ ôàêòîðîâ, ïðàâî-
ìåðíî äîïóùåíèå î íîðìàëüíîì çàêîíå ðàñïðåäåëåíèÿ ýòîé ñëó÷àé-
íîé âåëè÷èíû, ÷òî ïîäòâåðæäàåòñÿ ñòàòèñòè÷åñêîé îáðàáîòêîé ðå-
çóëüòàòîâ èçìåðåíèé òîëùèí ïîêðûòèÿ íàòóðíûõ èçäåëèé.
 ýòîì ñëó÷àå âûðàæåíèÿ äëÿ íîðìàòèâíîãî êîýôôèöèåíòà
áåçîïàñíîñòè ìîæíî çàïèñàòü â âèäå
kUS
pdd
=+1,
(6.7)
ãäå
U
p
— êâàíòèëü íîðìàëüíîãî ðàñïðåäåëåíèÿ;
S
d
— äèñïåðñèÿ
òîëùèíû ïîêðûòèÿ.
Ïðè íàëè÷èè ìàòåìàòè÷åñêèõ çàâèñèìîñòåé òîëùèíû ïîêðûòèÿ
(èëè èñõîäíûõ äàííûõ äëÿ åå ðàñ÷åòà) îò âëèÿþùèõ ôàêòîðîâ çíà÷å
-
íèå êîýôôèöèåíòà áåçîïàñíîñòè ìîæíî ðàññ÷èòàòü ìåòîäîì ñòàòè
-
ñòè÷åñêîãî ìîäåëèðîâàíèÿ (Ìîíòå-Êàðëî), èñõîäÿ èç óðîâíÿ ðàñ
-
ñåÿíèÿ ñîîòâåòñòâóþùèõ ôàêòîðîâ èëè ïóòåì ñòàòèñòè÷åñêîãî àíà
-
ëèçà ýêñïåðèìåíòàëüíûõ äàííûõ, ïîëó÷åííûõ ñ èñïîëüçîâàíèåì
ïëàíèðîâàíèÿ ýêñïåðèìåíòà.
Ýòîò àíàëèç óäîáíî ïðîâîäèòü ïî ãðóïïàì íåçàâèñèìûõ ôàêòîðîâ:
kUS
pi
i
I
dd
d=+
=
∑
1
2
1
05
(/ ) ,
,
íîì
(6.8)
ãäå
S
id
— ñðåäíåå êâàäðàòè÷íîå îòêëîíåíèå òîëùèíû ïîêðûòèÿ ïîä
âëèÿíèåì ðàññåÿíèÿ i-é ãðóïïû íåçàâèñèìûõ ôàêòîðîâ.
Ê ÷èñëó ôàêòîðîâ, ðàññåÿíèå êîòîðûõ âëèÿåò íà ðàññåÿíèå òîë
-
ùèíû ïîêðûòèÿ, îòíîñÿòñÿ ôàêòîðû îñíîâíîé ðàáîòû (òåìïåðàòóðà
ïðîäóêòîâ ñãîðàíèÿ, äàâëåíèå â êàìåðå äâèãàòåëÿ, ñêîðîñòü ïîòîêà
Ðàñ÷åò è ïðîåêòèðîâàíèå âíóòðåííåé òåïëîçàùèòû êîðïóñà 103

ïðîäóêòîâ ñãîðàíèÿ, âðåìÿ ðàáîòû äâèãàòåëÿ, õèìè÷åñêèé ïîòåíöè
-
àë ïðîäóêòîâ ñãîðàíèÿ, äåôîðìàöèÿ ïîêðûòèÿ è äð.); òåõíîëîãè÷å
-
ñêèå (äàâëåíèå ïðåññîâàíèÿ, òåìï íàãðåâà, òåìïåðàòóðà íàãðåâà,
âðåìÿ âûäåðæêè, òåìï îõëàæäåíèÿ); ïîëóôàáðèêàòà (ïðèðîäà ñû
-
ðüÿ, ñîäåðæàíèå êîìïîíåíò, ñòåïåíü íåîäíîðîäíîñòè ñòðóêòóðû).
Íàðÿäó ñ ýòèìè ôàêòîðàìè ñëåäóåò ó÷èòûâàòü òî÷íîñòü èçãîòîâ
-
ëåíèÿ ïîêðûòèÿ è èçìåðåíèÿ åãî òîëùèíû.
6.2. Ïîñòàíîâêà çàäà÷è íåñòàöèîíàðíîãî ïðîãðåâà
è óíîñà ìàññû âíóòðåííåãî ïîêðûòèÿ
6.2.1. Óðàâíåíèå íåñòàöèîíàðíîé òåïëîïðîâîäíîñòè
ñ êðàåâûìè óñëîâèÿìè äëÿ ñëó÷àÿ ÿâíîãî ó÷åòà
âíóòðåííåãî è ïîâåðõíîñòíîãî óíîñà ìàññû
Äëÿ ðåøåíèÿ çàäà÷è íåñòàöèîíàðíîãî ïðîãðåâà ñòåíêè ñ ïîêðû-
òèåì èñïîëüçóåòñÿ îäíîìåðíîå óðàâíåíèå íåñòàöèîíàðíîé òåïëî-
ïðîâîäíîñòè, çàïèñàííîå â ñèñòåìå êîîðäèíàò OY, íà÷àëî êîòîðîé
ñâÿçàíî ñ èñõîäíûì ïîëîæåíèåì ðàáî÷åé ïîâåðõíîñòè ïîêðûòèÿ, à
îñü Y íàïðàâëåíà ïåðïåíäèêóëÿðíî ê íåé (ïîïåðåê ñòåíêè). Óðàâíå-
íèå ñîäåðæèò ÷ëåíû, ó÷èòûâàþùèå ïîãëîùåíèå òåïëîòû ïðè òåðìè-
÷åñêîì ðàçëîæåíèè ìàòåðèàëà ïîêðûòèÿ è âëèÿíèå ôèëüòðàöèè ãà-
çîîáðàçíûõ ïðîäóêòîâ ðàçëîæåíèÿ íà ïðîãðåâ ïîêðûòèÿ [14]:
() ,1 −ϕ
′′
=
−
′′ ′′
−
∂
∂
∂
∂
∂
∂
∂
∂
rl wcmc
ðð
T
ty
T
y
T
y
S
(6.9)
ãäå j — òåêóùàÿ ïîðèñòîñòü ïîêðûòèÿ;
′
r
— ïëîòíîñòü êàðêàñà ïî
-
ðèñòîãî ìàòåðèàëà;
′
c
ð
— òåïëîåìêîñòü êàðêàñà; Ò — òåìïåðàòóðà; t —
âðåìÿ; ó — êîîðäèíàòà;
l
S
— ýôôåêòèâíàÿ òåïëîïðîâîäíîñòü ìàòå
-
ðèàëà, ó÷èòûâàþùàÿ êîêñîâàíèå êàðêàñà è ïåðåíîñ òåïëîòû èçëó÷å
-
íèåì â ïîðàõ;
′′
m
— ìàññîâàÿ ñêîðîñòü (ôèëüòðàöèè ãàçîâ ïèðîëèçà;
′′
c
p
— òåïëîåìêîñòü ãàçîâ ïèðîëèçà;
w = QR
SS
— îáúåìíàÿ ñêîðîñòü
ïîãëîùåíèÿ òåïëîòû ïðè ïèðîëèçå;
Q
S
— ñóììàðíûé òåïëîâîé ýô
-
ôåêò ïðîöåññà ïèðîëèçà;
R
S
— îáúåìíàÿ ñêîðîñòü ïðîöåññà ïèðîëèçà.
Óðàâíåíèå òåïëîïðîâîäíîñòè (6.9) ìîæåò áûòü óïðîùåíî çà ñ÷åò
îáúåäèíåíèÿ òåïëîïðîâîäíûõ è ôèëüòðàöèîííûõ ÷ëåíîâ åãî ïðàâîé
÷àñòè. Ñ ýòîé öåëüþ ôèëüòðàöèîííûé ÷ëåí ïðåäñòàâëÿåòñÿ â ôîðìå
′′
=
mñ
v
ð
m
T
v
T
v
¶
¶
¶
¶
¶
¶
l ,
(6.10)
104 Ãëàâà 6
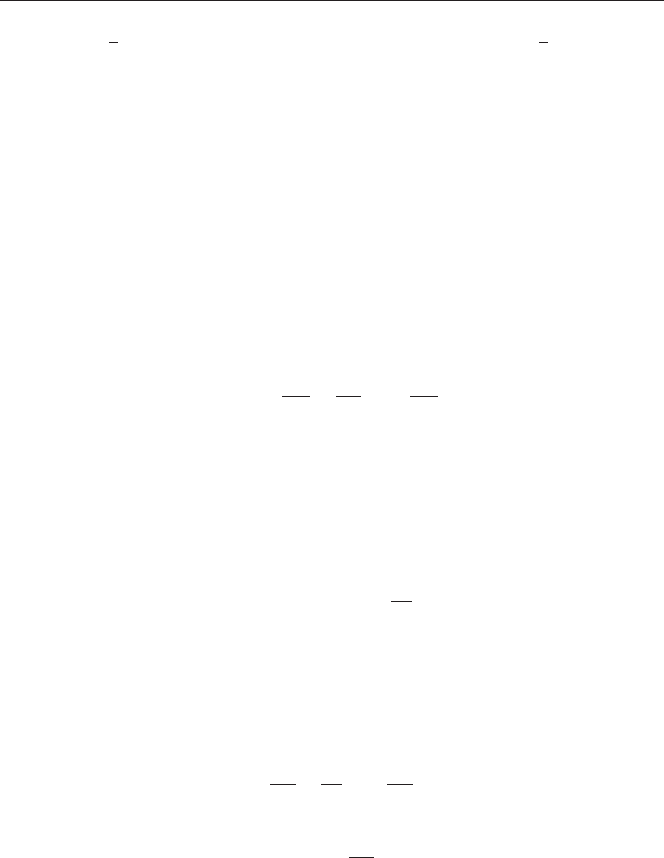
ãäå
l
m
m=
′′
ct
p
d()
— “êîíâåêòèâíàÿ” òåïëîïðîâîäíîñòü;
c
p
— ñðåäíå-
èíòåãðàëüíîå çíà÷åíèå òåïëîåìêîñòè ãàçà (ïàðà), çàïîëíÿþùåãî
ïîðû, â èíòåðâàëå òåìïåðàòóð T
íð
≤
Ò
≤
T
ï
;
d()t
— ðàññòîÿíèå ïî êî
-
îðäèíàòå ó ìåæäó èçîòåðìàìè T
íð
è
Tt
ï
()
; íð — íà÷àëî òåðìè÷åñêîãî
ðàçëîæåíèÿ ìàòåðèàëà ïîêðûòèÿ; ï — ïîâåðõíîñòü ïîêðûòèÿ.
Âõîäÿùàÿ â ôîðìóëó äëÿ “êîíâåêòèâíîé” òåïëîïðîâîäíîñòè
ìàññîâàÿ ñêîðîñòü ôèëüòðàöèè ãàçîâ ïèðîëèçà îïðåäåëÿåòñÿ èç ñîîò
-
íîøåíèÿ
′′
=−
∂
mKrd
0
1(),
(6.11)
ãäå
d
∂
— ñêîðîñòü ïåðåìåùåíèÿ ôðîíòà òåðìè÷åñêîãî ðàçëîæåíèÿ
(äåñòðóêöèè) â ãëóáü ïîêðûòèÿ.
Ïîñëå ïîäñòàíîâêè ôîðìóëû (6.10) â óðàâíåíèå (6.9) îíî ïðåîá
-
ðàçóåòñÿ ê âèäó
()1 −
′′ ′′
=
−jr l w
¶
¶
¶
¶
¶
¶
c
p
m
T
ty
T
y
S
, (6.12)
ãäå
lll
SS
mm
=−
— ýôôåêòèâíàÿ òåïëîïðîâîäíîñòü, ó÷èòûâàþùàÿ
ôèëüòðàöèþ ãàçîîáðàçíûõ ïðîäóêòîâ òåðìè÷åñêîãî ðàçëîæåíèÿ ìà-
òåðèàëà.
Âûðàæåíèå äëÿ îáúåìíîé ñêîðîñòè ïðîöåññà ïèðîëèçà, âõîäÿ-
ùåå â èñòî÷íèêîâûé ÷ëåí óðàâíåíèÿ (6.12), èìååò âèä
RK
t
S
=−
∂
∂
r
c
0
1(),
(6.13)
ãäå
r
0
— íà÷àëüíîå çíà÷åíèå ïëîòíîñòè ìàòåðèàëà; Ê— êîêñîâîå
÷èñëî;
c
— ñòåïåíü çàâåðøåííîñòè ïðîöåññà òåðìè÷åñêîãî ðàçëîæå
-
íèÿ ìàòåðèàëà.
Ïîñëå ïîäñòàíîâêè (6.13) â (6.12) îíî ïðèîáðåòàåò âèä
C
T
ty
T
y
m
ef
∂
∂
∂
∂
∂
∂
=
l
S
,
(6.14)
ãäå
CcKQ
T
ef
=−ϕ
′′
+−
∂
∂
() ( )11
0
rr
c
S
— îáúåìíàÿ òåïëîåìêîñòü
ìàòåðèàëà, ó÷èòûâàþùàÿ òåïëîâîé ýôôåêò ïðîöåññà òåðìè÷åñêîãî
ðàçëîæåíèÿ ìàòåðèàëà.
Óðàâíåíèå íåñòàöèîíàðíîé òåïëîïðîâîäíîñòè (6.14) ïî ôîðìå
àíàëîãè÷íî íàèáîëåå øèðîêî ïðèìåíÿåìîìó íà ïðàêòèêå óðàâíå
-
íèþ òåïëîïðîâîäíîñòè áåç ôèëüòðàöèîííîãî è èñòî÷íèêîâîãî ÷ëå
-
íîâ ïðàâîé ÷àñòè. Óðàâíåíèå òåïëîïðîâîäíîñòè â òàêîé ôîðìå ïðè
-
Ðàñ÷åò è ïðîåêòèðîâàíèå âíóòðåííåé òåïëîçàùèòû êîðïóñà 105

ìåíÿåòñÿ äëÿ ñòåíêè êîðïóñà, êîòîðàÿ íå íàãðåâàåòñÿ äî òåìïåðàòó
-
ðû íà÷àëà òåðìè÷åñêîãî ðàçëîæåíèÿ:
rl
00
0
ñ ==
∂
∂
∂
∂
∂
∂
T
ty
T
y
,
(6.15)
ãäå
rl
00
0
,,ñ
— ïëîòíîñòü, òåïëîåìêîñòü è òåïëîïðîâîäíîñòü ìàòå
-
ðèàëà ñòåíêè â èñõîäíîì ñîñòîÿíèè.
Êðàåâûå óñëîâèÿ ê óðàâíåíèÿì (6.14), (6.15) çàïèñûâàþòñÿ â ñëå
-
äóþùåì âèäå.
Íà÷àëüíîå óñëîâèå:
Ty Ty(, ) ().0 =
(6.16)
Ãðàíè÷íîå óñëîâèå íà ïîâåðõíîñòè âíóòðåííåãî ïîêðûòèÿ:
−
=−
′
−++
∂
∂
=−
lh
a
S
T
yc
yy
k
p
q
mII
ï
ïãï ý
ÔÀ
0
()
()
ôãï
s TT mQ
yy
44
−+
(6.17)
èëè
−
=−+
=−
la
¶
¶
SS
T
y
yy
yy
TT mQ
ï
ãï
0
() ,
ãäå
a
k
— êîýôôèöèåíò êîíâåêòèâíîãî òåïëîîáìåíà ìåæäó ãàçîâûì
ïîòîêîì è ïîâåðõíîñòüþ ïîêðûòèÿ;
a
aS
= fxt(,)
— “ñóììàðíûé”
êîýôôèöèåíò òåïëîîáìåíà, âêëþ÷àþùèé ëó÷èñòóþ ñîñòàâëÿþùóþ;
Tfxt
ãò
= (,)
— òåìïåðàòóðà â ÿäðå ïîòîêà, îìûâàþùåãî ðàáî÷óþ ïî
-
âåðõíîñòü;
xxd= /
— îòíîñèòåëüíàÿ äóãîâàÿ êîîðäèíàòà, îòñ÷èòû
-
âàåìàÿ îò öåíòðà ê ïåðèôåðèè äíèùà; d— äèàìåòð êîðïóñà;
h
q
—
êîýôôèöèåíò âäóâà (äëÿ òóðáóëåíòíîãî ïîòîêà
h
q
= 0,2); À
ýô
— ðàñ
-
÷åòíàÿ èëè ýìïèðè÷åñêàÿ ôóíêöèÿ ðàäèàöèîííûõ ïàðàìåòðîâ ïðè
-
ñòåííîãî ñëîÿ ãàçîâîãî ïîòîêà è ïîâåðõíîñòè; s — ïîñòîÿííàÿ Ñòå
-
ôàíà—Áîëüöìàíà; m
y
, Q
y
— ìàññîâàÿ ñêîðîñòü è òåïëîâîé ýôôåêò
ïîâåðõíîñòíîãî óíîñà ìàññû.
Óñëîâèÿ íà ãðàíèöàõ ìåæäó ñëîÿìè:
ll
∂
∂
∂
∂
=
==
=+
T
y
T
y
yy
yy
m
m
0
0
,
(6.18)
|
|
TT
yy
yy
m
m
=−
=+
=
0
0
,
(6.19)
106 Ãëàâà 6

ãäå
y
m
— êîîðäèíàòà m-é ãðàíèöû ìåæäó ñëîÿìè. Óñëîâèå íà íàðóæ
-
íîé ïîâåðõíîñòè ñòåíêè*:
l
∂
∂
=
=−
T
y
yy
m
0
0.
(6.20)
Äëÿ öèëèíäðè÷åñêîé ÷àñòè ñîñóäà óðàâíåíèå íåñòàöèîíàðíîé
òåïëîïðîâîäíîñòè ïðåäñòàâëÿåòñÿ â ôîðìå
Ñ( ) ( ) ,TrT
T
tr
T
r
∂
∂
∂
∂
=
1
l
(6.14¢ )
rRR t
m
∈→(, ); ,
0
0
ãäå
CT p c() ;=
00
ll()t =
0
ïðè
TT<
íð
;
ÑT C T() ();=
ef
ll() ()TT
m
=
S
ïðè
TT>
íð
;
R
0
, R
m
— çíà÷åíèÿ ðàäèóñà âíóòðåííåé ïîâåðõíîñòè è
m-é ãðàíèöû ìåæäó ñëîÿìè îáîëî÷êè; T
íð
— òåìïåðàòóðà íà÷àëà òåð-
ìè÷åñêîãî ðàçëîæåíèÿ ìàòåðèàëà.
Ïðè ìàëûõ çíà÷åíèÿõ îòíîøåíèÿ òîëùèíû îáîëî÷êè ê ðàäèóñó
åå êðèâèçíû óðàâíåíèå (6.14¢ ) ñòàíîâèòñÿ ýêâèâàëåíòíûì óðàâíåíè-
ÿì (6.14), (6.15). Ïîñêîëüêó ôîðìà (6.14¢ ) ÿâëÿåòñÿ áîëåå îáùåé, êî-
íå÷íî-ðàçíîñòíîå ðåøåíèå óðàâíåíèÿ íåñòàöèîíàðíîé òåïëîïðî-
âîäíîñòè áóäåì ðàññìàòðèâàòü íèæå ïðèìåíèòåëüíî ê ýòîé ôîðìå
åãî ïðåäñòàâëåíèÿ.
6.2.2. Ðàñ÷åò ñêîðîñòè ïîâåðõíîñòíîãî óíîñà ìàññû
îáóãëåííîãî ñëîÿ ïîêðûòèÿ
 ðàññìàòðèâàåìîì ñëó÷àå ïîâåðõíîñòíûé óíîñ ìàññû îáóãëåí
-
íîãî ñëîÿ (ÎÑ) ïîêðûòèÿ îáóñëîâëåí õèìè÷åñêèìè ðåàêöèÿìè óãëå
-
ðîäà ñ ãàçàìè Î, Î
2
,ÑÎ
2
,H
2
O. Ýòè ðåàêöèè ïðîòåêàþò â äèôôóçèîí
-
íîì ðåæèìå, êîãäà ñêîðîñòü ðåàêöèè íå çàâèñèò îò òåìïåðàòóðû ïî
-
âåðõíîñòè ÎÑ è îïðåäåëÿåòñÿ èíòåíñèâíîñòüþ òåïëîìàññîîáìåíà
ïîâåðõíîñòè ñ ãàçîâûì ïîòîêîì. Ïðè äîïóùåíèè î ðàâíîìåðíîì ìå
-
õàíè÷åñêîì óíîñå ÷àñòèö íàïîëíèòåëÿ ïî ìåðå âûãîðàíèÿ óãëåðîäà
ÎÑ äëÿ ðàñ÷åòà ìàññîâîé ñêîðîñòè õèìè÷åñêîãî óíîñà îáóãëåííîãî
ñëîÿ ìîæíî èñïîëüçîâàòü ôîðìóëó âèäà (6.12), ãäå
a
x
ð
ñ
— êîýôôèöè
-
Ðàñ÷åò è ïðîåêòèðîâàíèå âíóòðåííåé òåïëîçàùèòû êîðïóñà 107
* Ââèäó òîãî, ÷òî ñòåíêà ÿâëÿåòñÿ “òåðìè÷åñêè òîëñòîé”, âíóòðè íåå ìîæíî âû
-
äåëèòü óñëîâíóþ ãðàíèöó ñ êîîðäèíàòîé
′′
y
ï
,
íà êîòîðîé â êîíöå òåïëîâîãî âîçäåéñòâèÿ
òåìïåðàòóðà ïîâûøàåòñÿ íå áîëåå ÷åì íà 3 Ê. Îíà è ðàññìàòðèâàåòñÿ â êà÷åñòâå íà
-
ðóæíîé (òåïëîèçîëèðîâàííîé) ãðàíèöû ðàñ÷åòíîé îáëàñòè.

åíò ìàññîîáìåíà ìåæäó ïîòîêîì ïðîäóêòîâ ñãîðàíèÿ è ïîâåðõíîñòüþ
ÒÇÏ; B
m
— õèìè÷åñêèé ïîòåíöèàë ïðîäóêòîâ ñãîðàíèÿ;
K
ÒÇÌ
— êîê
-
ñîâîå ÷èñëî ÒÇÌ;
m
í
— ìàññîâàÿ äîëÿ íàïîëíèòåëÿ â ÒÇÌ;
′
ð
,
ð
í
—
ïëîòíîñòè êàðêàñà ÎÑ è íàïîëíèòåëÿ;
t
*
— âðåìÿ íà÷àëà õèìè÷åñêî
-
ãî óíîñà ìàññû ÎÑ;
k
x
— êîýôôèöèåíò ñîãëàñîâàíèÿ ïðèíÿòîé ìî
-
äåëè õèìè÷åñêîãî óíîñà ñ ýêñïåðèìåíòîì.
·
,
*
m
tt
y
m
ð
kBK
ñK m
m
K
=−
−
′
0
1
ïðè
êê ÒÇÌ
ÒÇÌ í
í
ÒÇÌ í
p
a
r
r
ïðè ttf
*
.
(6.21)
Äëÿ ðåàêöèé óãëåðîäà ñ ïåðå÷èñëåííûìè âûøå õèìè÷åñêè àê
-
òèâíûìè êîìïîíåíòàìè ïðîäóêòîâ ñãîðàíèÿ èõ õèìè÷åñêèé ïîòåí
-
öèàë ìîæåò áûòü ðàññ÷èòàí ïî ôîðìóëå
()
B
m
M
M
=+++
ñ
ã
HO CÎ
22
mm m m
00
2
,
(6.22)
ãäå
MM
ñã
,
— ìîëåêóëÿðíûå ìàññû óãëåðîäà è ïðîäóêòîâ ñãîðàíèÿ;
m
i
— ìîëüíàÿ äîëÿ i-ãî êîìïîíåíòà (i =Î,Î
2
,Í
2
Î, ÑÎ
2
).
Âðåìÿ íà÷àëà õèìè÷åñêîãî óíîñà îáóãëåííîãî ñëîÿ îïðåäåëÿåòñÿ
èç óñëîâèé:
à) ïðåâûøåíèÿ êîýôôèöèåíòîì ìàññîîáìåíà íóëåâîãî çíà÷åíèÿ
ïðè ñíèæåíèè ìàññîâîé ñêîðîñòè âäóâà äî ñîîòâåòñòâóþùåãî óðîâíÿ
a
x
ð
tt
ñ
≥
=
*
;0
(6.23)
á) ðàâåíñòâà ìàññîâîé ñêîðîñòè âäóâà ãàçîâ ïèðîëèçà êðèòè÷å
-
ñêîìó çíà÷åíèþ ïðè äàëüíåéøåì åå óìåíüøåíèè
*
|
·
()
·
.
*
*
′′
≤
=
mt m
tt
ï
(6.24)
Ôîðìóëó äëÿ îïðåäåëåíèÿ
m
*
ìîæíî ïîëó÷èòü èç ïðèáëèæåííî
-
ãî àíàëèçà ïðîöåññîâ òåïëîìàññîïåðåíîñà â ïîãðàíè÷íîì ñëîå, îá
-
ðàçóþùåìñÿ ó ïîâåðõíîñòè ÒÇÏ, â ïðåäïîëîæåíèè î ñëàáîì âëèÿ
-
íèè õèìè÷åñêèõ ðåàêöèé íà äèôôóçèþ êîìïîíåíòîâ ãàçîâîé ñìåñè
è ïåðåíîñ òåïëîòû, à òàêæå î ðàâåíñòâå ÷èñåë Ïðàíäòëÿ, Øìèäòà è
108 Ãëàâà 6
* Ìàññîâàÿ ñêîðîñòü âäóâà ãàçîâ ïèðîëèçà óáûâàåò ïî âðåìåíè â ñâÿçè ñ óìåíü
-
øåíèåì ñêîðîñòè äåñòðóêöèè ÒÇÏ. Ïîýòîìó âíà÷àëå ïåðåñòàåò “ðàáîòàòü” ôèçè÷å
-
ñêèé ýôôåêò îòòåñíåíèÿ ïîãðàíè÷íîãî ñëîÿ ïîòîêà ïðîäóêòîâ ñãîðàíèÿ îò ïîâåðõíî
-
ñòè îáóãëåííîãî ñëîÿ, à çàòåì — õèìè÷åñêèé ýôôåêò âçàèìîäåéñòâèÿ ãàçîâ ïèðîëèçà ñ
àêòèâíûìè êîìïîíåíòàìè ïðîäóêòîâ ñãîðàíèÿ [5].

Ëüþèñà, îòêóäà âûòåêàåò ïîäîáèå îòíîñèòåëüíûõ (ïðèâåäåííûõ)
ïðîôèëåé êîíöåíòðàöèè ïñåâäîâåùåñòâà è ýíòàëüïèè:
~~
~~
,
ÑÑ
ÑÑ
ï
ã
ï
ãï
ï
−
−
−
−
=
II
II
(6.25)
ãäå
~
ÑÑ Ñ
a
=−
0
n
— êîíöåíòðàöèÿ ïñåâäîâåùåñòâà;
Ñ
0
,Ñ
a
— êîíöåí
-
òðàöèÿ îêèñëÿþùèõ è õèìè÷åñêè àêòèâíûõ êîìïîíåíòîâ â ïðîäóêòàõ
ïèðîëèçà;
n
— ñòåõèîìåòðè÷åñêîå ñîîòíîøåíèå; I—ýíòàëüïèÿ.
Ñ ó÷åòîì ñîîòíîøåíèÿ (6.25) èç óñëîâèé áàëàíñà ìàññû è ýí
-
òàëüïèè íà ïîâåðõíîñòè îãíåçàùèòû ïîëó÷àåòñÿ âûðàæåíèå äëÿ êîí
-
öåíòðàöèè ïñåâäîâåùåñòâà íà ýòîé ïîâåðõíîñòè âèäà
~
,
~~
Ñ
ï
ãï
ÑÑ
=
+
′′
+
B
B1
(6.26)
çäåñü
B=
a
m
/ñ
ð
·
′′
ï
ê
— ïàðàìåòð âäóâà.
Ïîñêîëüêó â ìîìåíò âðåìåíè
t
*
ôðîíò âçàèìîäåéñòâèÿ ãàçîâ ïè-
ðîëèçà ñ ïðîäóêòàìè ñãîðàíèÿ äîñòèãàåò ïîâåðõíîñòè è
~
Ñ
ï
ñòàíîâèò-
ñÿ ðàâíûì íóëþ, èç âûðàæåíèÿ (6.26) ñëåäóåò, ÷òî
B
*
~~
.
′′
=−
′′
=ÑÑÑ
ïãã
0
(6.27)
Îòñþäà ïðè
~~
,
′′
=−ÑÑ
ï
n
a
ïåðåõîäÿ îò êîíöåíòðàöèé ê ìîëüíûì
äîëÿì, ïîëó÷àåì èñêîìóþ ôîðìóëó äëÿ êðèòè÷åñêîãî çíà÷åíèÿ ìàñ-
ñîâîé ñêîðîñòè âûõîäà ãàçîâ ïèðîëèçà â âèäå
·
*
.mk
vm
p
c
=
a
ê
(6.28)
Âõîäÿùèé â íåå êîýôôèöèåíò
k
vm
îïðåäåëÿåòñÿ èç ñîîòíîøåíèÿ
k
vm
i
i
i
M
M
v
=
′′
′′
∑∑
1
ã
m
m
b
b
b
b
,
ãäå
m
i
— ìîëüíàÿ äîëÿ i-ãî îêèñëÿþùåãî êîìïîíåíòà â ïîòîêå ïðî
-
äóêòîâ ñãîðàíèÿ;
′′
m
b
— ìîëüíàÿ äîëÿ õèìè÷åñêè àêòèâíûõ êîìïîíåíò â
ãàçàõ ïèðîëèçà (b =Í
2
,ÑH
4
,Ñ
2
Í
2
è ò.ï.);
MM
ã
,
′′
b
— ìîëåêóëÿðíûå
ìàññû ïðîäóêòîâ ñãîðàíèÿ è b-êîìïîíåíòà ãàçîâ ïèðîëèçà;
v
ib
— ñòå
-
õèîìåòðè÷åñêèé êîýôôèöèåíò â õèìè÷åñêîé ðåàêöèè i-ãî îêèñëÿþùå
-
ãî êîìïîíåíòà ïðîäóêòîâ ñãîðàíèÿ ñ b-êîìïîíåíòîì ãàçîâ ïèðîëèçà.
Ñêîðîñòü ëèíåéíîãî óíîñà ìàññû ÎÑ îïðåäåëÿåòñÿ ïî ôîðìóëå
vm
yy
=
′
−ϕ
·
/( )r 1
.
Ðàñ÷åò è ïðîåêòèðîâàíèå âíóòðåííåé òåïëîçàùèòû êîðïóñà 109

Ïî ýòèì äàííûì îïðåäåëÿåòñÿ òåêóùàÿ êîîðäèíàòà ðàáî÷åé ïî
-
âåðõíîñòè ïîêðûòèÿ
yt vdt
y
t
t
ï
() .
*
=
∫
(6.29)
Âõîäÿùàÿ â ãðàíè÷íîå óñëîâèå íà ðàáî÷åé ïîâåðõíîñòè ïîêðû
-
òèÿ òåïëîòà õèìè÷åñêîãî óíîñà ðàññ÷èòûâàåòñÿ ïî ôîðìóëå
QQ
xii
i
i
i
=
==
∑∑
mm
1
4
1
4
,
(6.30)
ãäå
m
i
— ìîëüíàÿ äîëÿ i-ãî õèìè÷åñêè àêòèâíîãî êîìïîíåíòà â ñî
-
ñòàâå ïðîäóêòîâ ñãîðàíèÿ;
Q
i
— òåïëîâîé ýôôåêò õèìè÷åñêîé ðåàê
-
öèè i-ãî êîìïîíåíòà ñ óãëåðîäîì, êÄæ/êã
Ñ
.
Òåïëîâûå ýôôåêòû õèìè÷åñêèõ ðåàêöèé àêòèâíûõ êîìïîíåíòîâ
ïðîäóêòîâ ñãîðàíèÿ ñ óãëåðîäîì ðàññ÷èòûâàþòñÿ ïî òåïëîòàì îáðà-
çîâàíèÿ èñõîäíûõ âåùåñòâ è ïðîäóêòîâ ñîîòâåòñòâóþùèõ ðåàêöèé ñ
ïîìîùüþ çàêîíà Ãåññà:
QvH vH
i
=−
∑∑
a
a
ab
b
b
DD,
(6.31)
ãäå
DDHH
ab
,
— òåïëîòû îáðàçîâàíèÿ a -ïðîäóêòà ðåàêöèè è b-èñ-
õîäíîãî âåùåñòâà; v
a
, v
b
— ñòåõèîìåòðè÷åñêèå êîýôôèöèåíòû.
Òåïëîòû îáðàçîâàíèÿ âåùåñòâ, ó÷àñòâóþùèõ ïðè âûñîêèõ òåì-
ïåðàòóðàõ â õèìè÷åñêèõ ðåàêöèÿõ ñ óãëåðîäîì îáóãëåííîãî ñëîÿ,
ïðèâåäåíû â òàáë. 6.1.
Ðåçóëüòàòû ðàñ÷åòà òåïëîâûõ ýôôåêòîâ ðåàêöèé õèìè÷åñêè àêòèâ
-
íûõ êîìïîíåíò ïðîäóêòîâ ñãîðàíèÿ ñ óãëåðîäîì îáóãëåííîãî ñëîÿ äàíû
â òàáë. 6.2. Ïðîâåðêà ïîëó÷åííûõ ðåçóëüòàòîâ ïóòåì èõ ñðàâíåíèÿ ñ
èìåþùèìèñÿ ýêñïåðèìåí
-
òàëüíûìè äàííûìè ïî òåï
-
ëîòàì ñãîðàíèÿ óãëåðîäà
ïîäòâåðäèëà ïðàâèëüíîñòü
110 Ãëàâà 6
Òàáëèöà 6.1
Òåïëîòû îáðàçîâàíèÿ âåùåñòâ,
ó÷àñòâóþùèõ â õèìè÷åñêèõ ðåàê
-
öèÿõ ñ óãëåðîäîì îáóãëåííîãî ñëîÿ
Õèìè÷åñêàÿ
ôîðìóëà
âåùåñòâà
Ìîëåêóëÿð
-
íàÿ ìàññà,
êã/ìîëü
Òåïëîòà îá
-
ðàçîâàíèÿ,
êÄæ/ìîëü
ÑÎ 0,028 –110,53
ÑÎ
2
0,044 –393,51
Í
2
Î 0,018 –286,03
Òàáëèöà 6.2
Òåïëîâûå ýôôåêòû ðåàêöèè óãëåðîäà ñ àêòèâíû
-
ìè êîìïîíåíòàìè ïðîäóêòîâ ñãîðàíèÿ
¹
ï/ï
Ðåàêöèÿ
Òåïëîâîé ýôôåêò
Q
i
,
êÄæ/(ìîëü × ñ)
Q
i
,
êÄæ/(êã × ñ)
1
Ñ+ή ÑÎ
–110,53 –92100
2
Ñ+Î
2
® ÑÎ
2
–393,51 –32792
3
Ñ+ÑÎ
2
® 2ÑÎ
+ 172,45 +14371
4
Ñ+Í
2
Î ® ÑÎ+Í
2
+ 175,50 +14625
Ïðèìå÷àíèå. Çíàê – îáîçíà÷àåò âûäåëåíèå,
+ — ïîãëîùåíèå òåïëîòû.
