Воробей В.В., Маркин В.Б. Основы технологии и проектирования корпусов ракетных двигателей

Подождите немного. Документ загружается.

Îñíîâíûå ïàðàìåòðû äâèãàòåëÿ:

— ìàññà çàðÿäà 6200 êã;

— óäåëüíûé èìïóëüñ íà óðîâíå ìîðÿ 213,5 ñ;

— ìàêñèìàëüíîå äàâëåíèå 55 áàð;

— äèàìåòð êðèòè÷åñêîãî ñå÷åíèÿ ñîïëà 190 ìì;

— äèàìåòð âûõîäíîãî ñå÷åíèÿ ñîïëà 900 ìì.

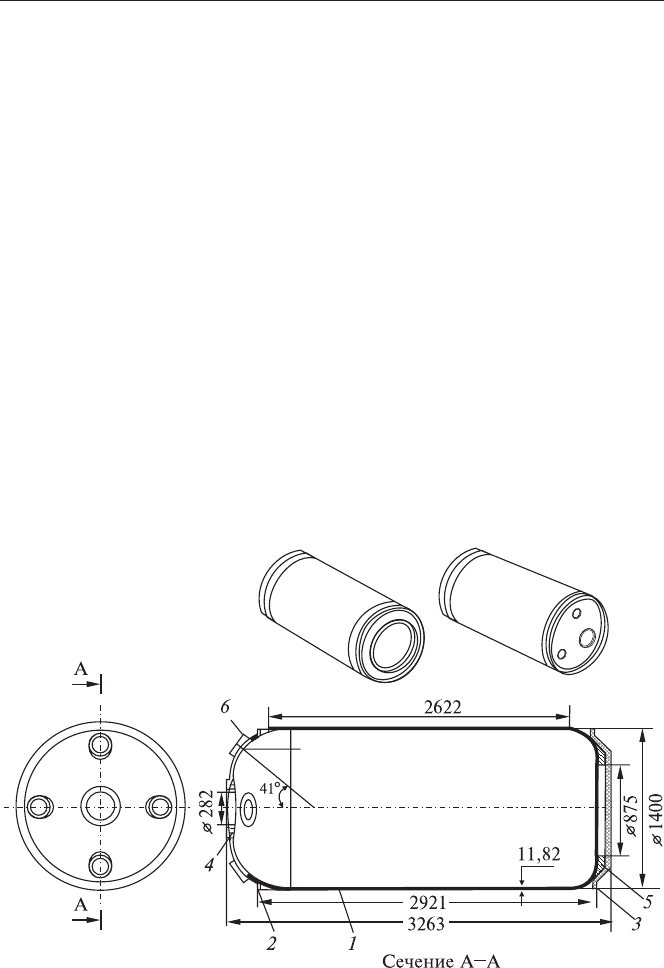
Ýñêèç êîðïóñà ñ óêàçàíèåì îñíîâíûõ ãàáàðèòíûõ ðàçìåðîâ

ïðåäñòàâëåí íà ðèñ. 4.1.

Ñ öåëüþ îïðåäåëåíèÿ ïàðàìåòðîâ òåïëîâîãî âîçäåéñòâèÿ íà òåï-

ëîçàùèòó âûáðàíû ôîðìà è ñîñòàâ íàïîëíèòåëÿ è ïðîâåäåíû ðàñ÷å-

Ãëàâà 4

Èñõîäíûå äàííûå

äëÿ ïðîåêòèðîâàíèÿ êîðïóñà äâèãàòåëÿ

Ðèñ. 4.1. Îñíîâíûå ãàáàðèòíûå ðàçìåðû êîðïóñà.

1 — ñèëîâàÿ îáîëî÷êà; 2 — óçåë ñîåäèíåíèÿ ïåðåäíèé è 3 — çàäíèé; 4 — ôëàíåö ïå

ðåäíèé è 5 — çàäíèé; 6 — îòâåðñòèÿ äëÿ óïðàâëåíèÿ òÿãîé.

òû: èçìåíåíèå ãåîìåòðèè íàïîëíèòåëÿ â ïðîöåññå ðàáîòû, à òàêæå

äàâëåíèÿ è ñêîðîñòè îáòåêàíèÿ âíóòðåííåé ïîâåðõíîñòè êîðïóñà

ïðîäóêòàìè ñãîðàíèÿ.

4.1. Ðàñ÷åò èçìåíåíèÿ

âî âðåìåíè ãåîìåòðèè íàïîëíèòåëÿ

è äàâëåíèÿ âíóòðè êîðïóñà

Èñõîäíûìè äàííûìè äëÿ ðàñ÷åòà ðàçãàðà íàïîëíèòåëÿ ÿâëÿþòñÿ

ãåîìåòðèÿ âíóòðåííåé ïîâåðõíîñòè êîðïóñà è ãåîìåòðèÿ íàïîëíèòå

ëÿ íà ìîìåíò íà÷àëà ãîðåíèÿ ïðè t =0(t — âðåìÿ). Îñíîâíûå õàðàê

òåðèñòèêè âûáðàííîãî íàïîëíèòåëÿ ìàðêè ANB-3066 ïðèâåäåíû â

òàáë. 4.1–4.3. Ãåîìåòðè÷åñêèå ïàðàìåòðû íàïîëíèòåëÿ ïðèâåäåíû íà

ðèñ. 4.1 [13].

82 Ãëàâà 4

Òàáëèöà 4.1

Ñîñòàâ (%) è áàëëèñòè÷åñêèå õàðàêòåðèñòèêè íàïîëíèòåëÿ ìàðêè

ANB-3066

Ñîñòàâ è õàðàêòåðèñòèêà íàïîëíèòåëÿ Çíà÷åíèå

Ïåðõëîðàò àììîíèÿ 66

Ïîëèáóòàäèåíîâàÿ êèñëîòà 12

Ýïîêñèäíàÿ ñìîëà 3

Àëþìèíèåâûé ïîðîøîê 19

Çàâèñèìîñòü ñêîðîñòè ãîðåíèÿ

= 20 °Ñ) 2,9(Ð/98 100)

0,3

¶¶lnu T/,

1/°Ñ 0,002

Ïëîòíîñòü, ã/ñì

1,77

Ìèíèìàëüíîå äàâëåíèå óñòîé÷èâîãî ãîðåíèÿ, ÌÏà 0,01

Ïóñòîòíûé óäåëüíûé èìïóëüñ, ì/ñ 2720

Òåìïåðàòóðà ãîðåíèÿ, Ê 3420

Ðàñõîäíûé êîìïëåêñ

, ì/ñ 1590

* Ïðè

ÌÏà;

= 01,

ÌÏà.

Òàáëèöà 4.2

Òåïëîôèçè÷åñêèå õàðàêòåðèñòèêè íàïîëíèòåëÿ ANB-3066

Õàðàêòåðèñòèêà Çíà÷åíèå

Óäåëüíàÿ òåïëîåìêîñòü, Äæ/(êã × Ê)

1377

Êîýôôèöèåíò òåïëîïðîâîäíîñòè, Âò/(ì × Ê)

0,24

Êîýôôèöèåíò ëèíåéíîãî ðàñøèðåíèÿ, 1/Ê

2 × 10

Ýêñïëóàòàöèîííûé èíòåðâàë òåìïåðàòóð, °Ñ –55 ... +55

Ìàêñèìàëüíàÿ òåìïåðàòóðà õðàíåíèÿ, °Ñ 50

Äëÿ îïðåäåëåíèÿ çà-

âèñèìîñòè îò âðåìåíè ïî-

âåðõíîñòè ãîðåíèÿ íàïîë-

íèòåëÿ íà ÷åðòåæ åãî

ïðîäîëüíîãî ñå÷åíèÿ íà-

íîñèëè ëèíèè ïðîìåæóòî÷íûõ ïîëîæåíèé ïîâåðõíîñòè ãîðåíèÿ,

ñîîòâåòñòâóþùèå òîëùèíàì ñãîðåâøåãî ñâîäà ê çàäàííûì ìîìåíòàì

âðåìåíè. Êðîìå òîãî, ñâîä íàïîëíèòåëÿ ðàçáèâàëñÿ íà ãåîìåòðè÷å-

ñêèå ôèãóðû ïðîñòîé ôîðìû. Â ðåçóëüòàòå ñîîòâåòñòâóþùèõ ãåîìåò-

ðè÷åñêèõ ðàñ÷åòîâ ïîëó÷åíà çàâèñèìîñòü ïëîùàäè ïîâåðõíîñòè ãîðå

íèÿ íàïîëíèòåëÿ

()S

îò òîëùèíû ñãîðåâøåãî ñâîäà

(),C

ïðåäñòàâëåí

íàÿ â òàáë. 4.4.

Äàâëåíèå â ñîñóäå â ïðîöåññå ãîðåíèÿ íàïîëíèòåëÿ ðàññ÷èòûâà

ëîñü èç óðàâíåíèÿ áàëàíñà ìàññû, ïðåäñòàâëåííîãî â âèäå ðàâåíñòâà

ïðèõîäà ãàçà ñ ïîâåðõíîñòè ãîðåíèÿ (Ï) ðàñõîäó ãàçà ÷åðåç ñå÷åíèå

âûõîäíîãî îòâåðñòèÿ (G):

Ï( ) ( ).tGt=

(4.1)

Ïðèõîä ãàçà ñ ïîâåðõíîñòè ãîðåíèÿ îïðåäåëÿåòñÿ èç ñîîòíî-

øåíèÿ

() () ().tUt St= r

(4.2)

Äëÿ ðàñ÷åòà ðàñõîäà ãàçà èñïîëüçóåòñÿ ôîðìóëà âèäà

Fpt

()

(4.3)

Èñõîäíûå äàííûå äëÿ ïðîåêòèðîâàíèÿ êîðïóñà äâèãàòåëÿ 83

Òàáëèöà 4.3

Õàðàêòåðèñòèêè è ðàâíîâåñíûé ñîñòàâ

ïðîäóêòîâ ñãîðàíèÿ íàïîëíèòåëÿ ANB-3066

ïðè äàâëåíèè 4,0 ÌÏà

Õàðàêòåðèñòèêà Çíà÷åíèå

Òåìïåðàòóðà, T, Ê 3415

Ìîëåêóëÿðíàÿ ìàññà,

, ã/ìîëü 27,9

Òåïëîåìêîñòü,

, Äæ/(êã × Ê)

3,76

Âÿçêîñòü,

× 10

,Í× ñ/ì

0,91

Òåïëîïðîâîäíîñòü,

, Âò/(ì × Ê)

1,28

Ïîêàçàòåëü àäèàáàòû, k 1,16

Ñîäåðæàíèå êîìïîíåíòîâ

(ìîë. äîëè)

Í 0,0454

0,3511

Î 0,0947

HCl 0,1157

0,0793

CO 0,2656

0,0086

0,3204

Òàáëèöà 4.4

Çàâèñèìîñòü ïëîùàäè ïîâåðõíî

ñòè ãîðåíèÿ íàïîëíèòåëÿ îò

òîëùèíû ñãîðåâøåãî ñâîäà

Ñ,ìì

7,44 0 9,22 200

7,85 20 5,99 220

8,01 40 8,93 240

7,98 60 8,91 260

8,88 80 8,90 280

9,36 100 8,88 300

9,83 120 8,83 320

10,28 140 8.81 340

9,82 160 8,72 360

9,51 180 8,68 380

Â ôîðìóëàõ (4.2), (4.3) èñ

ïîëüçîâàíû ñëåäóþùèå îáîçíà

÷åíèÿ: U(t) — òåêóùèå çíà÷åíèÿ

ñêîðîñòè ãîðåíèÿ íàïîëíèòåëÿ;

— çàäàííàÿ ïëîòíîñòü íàïîë

íèòåëÿ,

= 1770 êã/ì

;

— ïëî

ùàäü ñå÷åíèÿ âûõîäíîãî îòâåð

ñòèÿ,

= 3,1416

; R

— ðàäèóñ

âûõîäíîãî îòâåðñòèÿ, ïðè ðàñ÷eòå

= 0,128 ì;

pt()

— äàâëåíèå;

— êîýôôèöèåíò ðàñõîäà.

Òåêóùèå çíà÷åíèÿ ñêîðîñòè ãîðåíèÿ íàïîëíèòåëÿ ðàññ÷èòûâà-

þòñÿ ïî ôîðìóëå âèäà

Ut U pt() [ ()]=

, (4.4)

ãäå

, n

— ïàðàìåòðû çàêîíà ñêîðîñòè ãîðåíèÿ.

Ïîñëå ïîäñòàíîâêè çàâèñèìîñòè ñêîðîñòè ãîðåíèÿ íàïîëíèòåëÿ

îò äàâëåíèÿ (4.4) â ñîîòíîøåíèå (4.2) è íåñëîæíûõ ïðåîáðàçîâàíèé

ñ ó÷åòîì ôîðìóë (4.1) è (4.3) çàâèñèìîñòü äàâëåíèÿ â ñîñóäå îò âðå-

ìåíè èìååò âèä

UpS t

() .

()

/( )













−

(4.5)

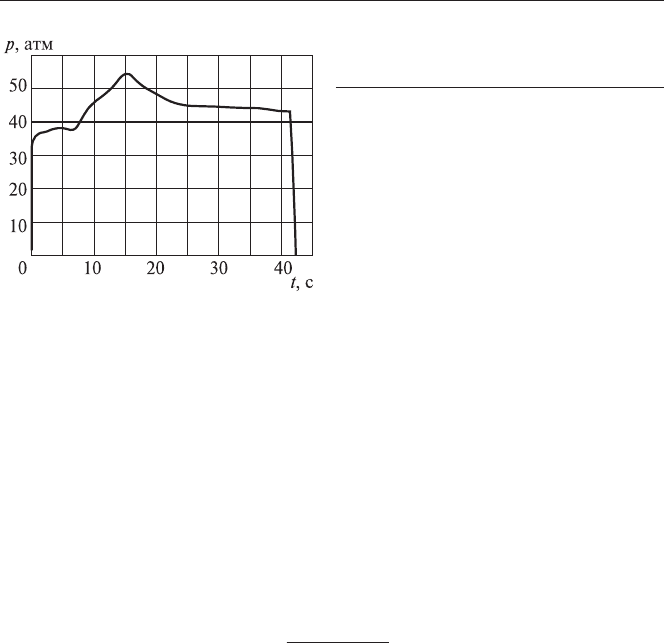
Ãðàôèê çàâèñèìîñòè îò âðåìåíè äàâëåíèÿ

pt()

ïðèâåäeí íà

ðèñ. 4.2.

4.2. Îïðåäåëåíèå ñêîðîñòè îáòåêàíèÿ ãàçîì

âíóòðåííåé ïîâåðõíîñòè êîðïóñà

Ñêîðîñòü îáòåêàíèÿ âíóòðåííåé ïîâåðõíîñòè ïåðåäíåãî äíèùà

êîðïóñà ðàññ÷èòûâàåòñÿ ïî ôîðìóëå

Vt VtStFt

ppp

() () ()/ ()=

, (4.6)

ãäå

()

— ñêîðîñòü îòòîêà ãàçîâ îò ïîâåðõíîñòè ãîðåíèÿ;

()

— ïëîùàäü ïîâåðõíîñòè ãîðåíèÿ â çîíå ïåðåäíåãî äíèùà;

84 Ãëàâà 4

Ðèñ. 4.2. Çàâèñèìîñòü îò âðåìåíè äàâ

ëåíèÿ âíóòðè êîðïóñà.

()

— òåêóùàÿ ïëîùàäü êîíè÷åñêîé ïîâåðõíîñòè, ÷åðåç êîòîðóþ

ãàçû âòåêàþò â öåíòðàëüíûé êàíàë*.

Ïðè ñíèæåíèè âåëè÷èíû

()

äî óðîâíÿ ñêîðîñòè îòòîêà ãàçîâ

îò ïîâåðõíîñòè ãîðåíèÿ íàïîëíèòåëÿ

()

çíà÷åíèÿì

()

ïðèñâàè-

âàþòñÿ çíà÷åíèÿ

()

, êîòîðûå ðàññ÷èòûâàþòñÿ ïî ôîðìóëå

Vt Ut t

() () / (),= rr

pt RT= ()/( ),

(4.7)

ãäå R

— ãàçîâàÿ ïîñòîÿííàÿ ïðîäóêòîâ ñãîðàíèÿ; Ò

— òåìïåðàòóðà

ïðîäóêòîâ ñãîðàíèÿ.

Ñêîðîñòü îáòåêàíèÿ âíóòðåííåé ïîâåðõíîñòè çàäíåãî äíà êîðïó

ñà íàõîäèòñÿ ïî ôîðìóëå

Vt VtStFt

ddd

() () ()/ (),=

(4.8)

ãäå

()

— òåêóùàÿ âî âðåìåíè ïëîùàäü êîíè÷åñêîé ïîâåðõíîñòè,

÷åðåç êîòîðóþ ãàçû âòåêàþò â âûõîäíîå îòâåðñòèå*;

()

— ïëîùàäü

ïîâåðõíîñòè ãîðåíèÿ â çîíå çàäíåãî äíèùà.

Ïðè ñíèæåíèè âåëè÷èíû

()

äî óðîâíÿ ñêîðîñòè îòòîêà ãàçîâ

îò ïîâåðõíîñòè ãîðåíèÿ íàïîëíèòåëÿ

()

âåëè÷èíå

()

(êàê è â

ïðåäûäóùåì ñëó÷àå) ïðèñâàèâàåòñÿ çíà÷åíèå

()

. Ðàññ÷èòàííûå ïî

îïèñàííîìó âûøå àëãîðèòìó çàâèñèìîñòè îò âðåìåíè ñêîðîñòåé îá

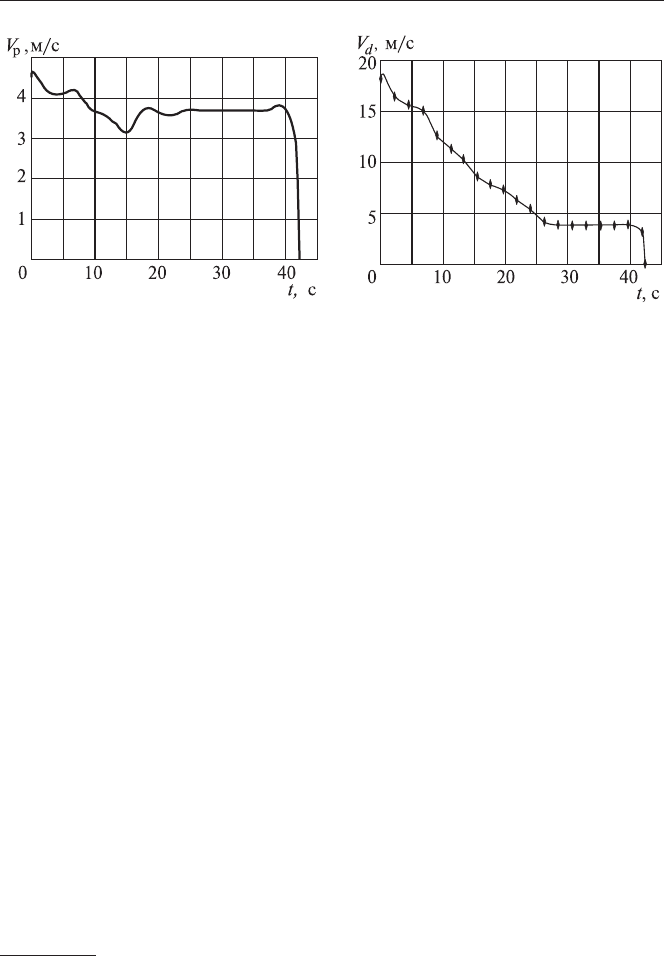
òåêàíèÿ ïðîäóêòàìè ñãîðàíèÿ ïåðåäíåãî è çàäíåãî äíèùà â ãðàôè

÷åñêîé ôîðìå ïðåäñòàâëåíû íà ðèñ. 4.3 è 4.4.

Èñõîäíûå äàííûå äëÿ ïðîåêòèðîâàíèÿ êîðïóñà äâèãàòåëÿ 85

Ðèñ. 4.3. Çàâèñèìîñòü îò âðåìåíè

ñêîðîñòåé îáòåêàíèÿ ïåðåäíåãî äíà.

Ðèñ. 4.4. Çàâèñèìîñòü îò âðåìåíè

ñêîðîñòåé îáòåêàíèÿ çàäíåãî äíà.

* Îáðàçóþùàÿ ýòîé êîíè÷åñêîé ïîâåðõíîñòè — îòðåçîê ïðÿìîé, ñîåäèíÿþùåé òî÷

êó íà òåêóùåé âõîäíîé êðîìêå öåíòðàëüíîãî êàíàëà íàïîëíèòåëÿ ñ òåêóùåé òî÷êîé íà

ïîâåðõíîñòè ïåðåäíåãî äíà â ìîìåíò åå âñêðûòèÿ (áåðåòñÿ èç ãåîìåòðè÷åñêîãî ðàñ÷åòà).

Ãëàâà 5

Ïðîåêòèðîâàíèå è ðàñ÷åò

ñèëîâîé îáîëî÷êè êîðïóñà

(ïðî÷íîñòè, æåñòêîñòè,

òåõíîëîãè÷åñêèõ àñïåêòîâ íàìîòêè)

Ïðîåêòèðîâî÷íûé ðàñ÷åò áàëëîíîâ äàâëåíèÿ, âûïîëíåííûõ èç

êîìïîçèöèîííûõ ìàòåðèàëîâ ìåòîäîì íåïðåðûâíîé íàìîòêè, ñâî

äèòñÿ ê îïðåäåëåíèþ ïðîåêòíûõ ïàðàìåòðîâ êîíñòðóêöèè, îáåñïå

÷èâàþùèõ óäîâëåòâîðåíèå ñëåäóþùèõ óñëîâèé:

1) îáåñïå÷åíèå ìèíèìàëüíîé ìàññû ïðîåêòèðóåìîé êîíñòðóê

öèè;

2) ñîõðàíåíèå òðåáóåìîé ïðî÷íîñòè (æåñòêîñòè) ïðè äåéñòâèè

ðàñ÷åòíûõ íàãðóçîê;

3) òåõíîëîãè÷åñêàÿ ðåàëèçóåìîñòü.

Îñíîâíûìè ïàðàìåòðàìè áàëëîíîâ äàâëåíèÿ, îïðåäåëÿåìûìè â

ïðîöåññå ïðîåêòèðîâàíèÿ, ÿâëÿþòñÿ [7]:

1) êîíòóðû äíèù áàëëîíîâ;

2) ðàñïðåäåëåíèå óãëîâ àðìèðîâàíèÿ (óãëîâ îðèåíòàöèè àðìè-

ðóþùèõ âîëîêîí îòíîñèòåëüíî ìåðèäèîíàëüíûõ ëèíèé ïîâåðõíîñòè

áàëëîíà);

3) êîëè÷åñòâî ñëîåâ àðìèðóþùåãî ìàòåðèàëà, îáðàçóþùèõ ñèëî

âóþ îáîëî÷êó.

5.1. Ìåòîäèêà ðàñ÷åòà

îïòèìàëüíûõ óãëîâ àðìèðîâàíèÿ

è êîíòóðîâ äíèù

Ïðè èçãîòîâëåíèè ñèëîâûõ îáîëî÷åê áàëëîíîâ äàâëåíèÿ ìåòî

äîì íåïðåðûâíîé íàìîòêè óêëàäêó àðìèðóþùèõ íèòåé íà ïîâåðõ

íîñòü îïðàâêè íàèáîëåå öåëåñîîáðàçíî ïðîèçâîäèòü ïî ãåîäåçè÷å

ñêèì ëèíèÿì ïîâåðõíîñòè [9]. Òðàåêòîðèÿ íàìîòêè ïðè ýòîì îïðåäå

ëÿåòñÿ èçâåñòíûì ñîîòíîøåíèåì òåîðèè Êëåðî:

r sin j = const

, (5.1)

ãäå r — ðàäèóñ îáîëî÷êè;

— óãîë àðìèðîâàíèÿ.

86 Ãëàâà 5

Öåëåñîîáðàçíîñòü òàêîé ñõåìû àðìèðîâàíèÿ îáóñëîâëåíà ñëå

äóþùèìè îáñòîÿòåëüñòâàìè:

1. Ïðè ãåîäåçè÷åñêîì àðìèðîâàíèè íèòü, óêëàäûâàåìàÿ íà îï

ðàâêó, íàõîäèòñÿ â ðàâíîâåñèè äàæå ïðè ñêîëü óãîäíî ìàëîì êîýô

ôèöèåíòå òðåíèÿ ìåæäó îïðàâêîé è íèòüþ, ïîñêîëüêó êàñàòåëüíûå

óñèëèÿ, äåéñòâóþùèå íà íèòü â ïîïåðå÷íîì íàïðàâëåíèè, â äàííîì

ñëó÷àå îòñóòñòâóþò [7].

2. Óñèëèÿ â íèòÿõ, óëîæåííûõ ïî ãåîäåçè÷åñêèì òðàåêòîðèÿì,

ïðè äåéñòâèè íà áàëëîí âíóòðåííåãî äàâëåíèÿ îêàçûâàþòñÿ ïîñòî

ÿííûìè ïî äëèíå, ÷òî ïîçâîëÿåò ñïðîåêòèðîâàòü ðàâíîïðî÷íóþ ñè

ëîâóþ êîíñòðóêöèþ [9].

Ðàâåíñòâî (5.1) ìîæåò áûòü ïåðåïèñàíî â ñëåäóþùåì âèäå:

rrsin j ==

const

. (5.2)

Çäåñü r

— ðàäèóñ ïîëþñíîãî îòâåðñòèÿ, ãäå, èñõîäÿ èç óñëîâèÿ íå-

ïðåðûâíîñòè íàìîòêè,

= 90°. Àíàëèçèðóÿ ïîñëåäíåå ñîîòíîøåíèå,

íåòðóäíî âèäåòü, ÷òî ãåîäåçè÷åñêàÿ íàìîòêà ðåàëèçóåìà òîëüêî â

ñëó÷àå, êîãäà ðàäèóñû ïîëþñíûõ îòâåðñòèé îäèíàêîâû. Åñëè æå ýòè

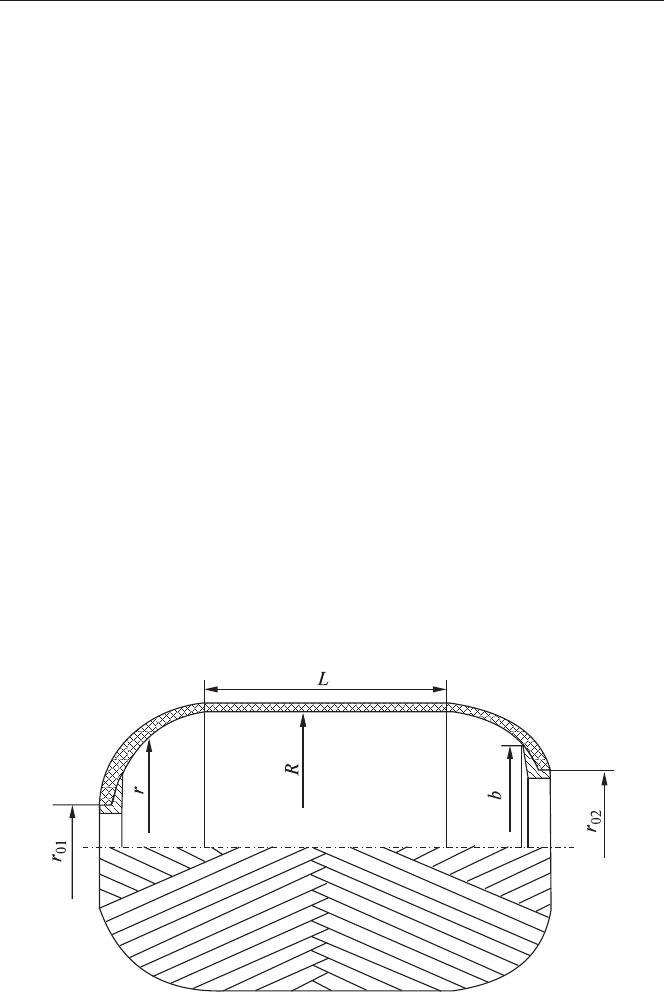
ðàäèóñû ðàçëè÷íû (ðèñ. 5.1), çíà÷åíèÿ ôóíêöèè Êëåðî

rsinj

ëåæàò â

äèàïàçîíå îò r

äî r

, ãäå r

— ðàäèóñû ïåðåäíåãî è çàäíåãî ïî-

ëþñíûõ îòâåðñòèé ñîîòâåòñòâåííî. Ïðè ýòîì óñëîâèå (5.2), î÷åâèä-

íî, íå âûïîëíÿåòñÿ, è òðàåêòîðèè óêëàäêè àðìèðóþùèõ íèòåé íà

÷àñòè áàëëîíà áóäóò îòëè÷àòüñÿ îò ãåîäåçè÷åñêèõ. Òàêóþ íàìîòêó

ïðèíÿòî íàçûâàòü íåãåîäåçè÷åñêîé [8].

Ïîñêîëüêó ïðè íåãåîäåçè÷åñêîé íàìîòêå àðìèðóþùàÿ íèòü óäåð-

æèâàåòñÿ îò ñîñêàëüçûâàíèÿ ñ ïîâåðõíîñòè îïðàâêè áëàãîäàðÿ ñèëàì

Ïðîåêòèðîâàíèå è ðàñ÷åò ñèëîâîé îáîëî÷êè êîðïóñà 87

Ðèñ. 5.1. Ñõåìà áàëëîíà äàâëåíèÿ.

òðåíèÿ, î÷åâèäíî, ñóùåñòâóåò ìèíèìàëüíîå çíà÷åíèå êîýôôèöèåíòà

òðåíèÿ ìåæäó íèòüþ è ïîâåðõíîñòüþ, îáåñïå÷èâàþùåå ñòàòè÷åñêîå

ðàâíîâåñèå íèòè. Ìàòåìàòè÷åñêè ýòî óñëîâèå ôîðìóëèðóåòñÿ ñëå

äóþùèì îáðàçîì [7]:

òð

q ≤ k ,

(5.3)

ãäå k

òð

— êîýôôèöèåíò òðåíèÿ;

— óãîë ìåæäó íîðìàëüþ ê ïîâåðõ

íîñòè îïðàâêè

è íîðìàëüþ ê òðàåêòîðèè óêëàäêè íèòè

íàçûâàå

ìûé óãëîì ãåîäåçè÷åñêîãî îòêëîíåíèÿ.

Ðóêîâîäñòâóÿñü îïðåäåëåíèåì óãëà ãåîäåçè÷åñêîãî îòêëîíåíèÿ è

èñïîëüçóÿ àïïàðàò äèôôåðåíöèàëüíîé ãåîìåòðèè, íåòðóäíî ïîëó

÷èòü âûðàæåíèå äëÿ òàíãåíñà óãëà ãåîäåçè÷åñêîãî îòêëîíåíèÿ ïðè

ìåíèòåëüíî ê óêëàäêå íèòè íà ïîâåðõíîñòü, îáðàçîâàííóþ âðàùåíè

åì êðèâîé r = r(z) âîêðóã îñè z:

tgq

=−

′

−

″

′

−

()

. (5.4)

Çäåñü è â äàëüíåéøåì

xj= r sin

— îáîçíà÷åíèå, ââåäeííîå äëÿ ôóíê-

öèè Êëåðî, à âåðõíèì øòðèõîì îáîçíà÷àåòñÿ îïåðàöèÿ äèôôåðåíöè-

ðîâàíèÿ ïî êîîðäèíàòå z.

Påàëèçóåìîñòü (ñ òî÷êè çðåíèÿ óñòîé÷èâîñòè íèòè íà îïðàâêå)

òðàåêòîðèé íåãåîäåçè÷åñêîé íàìîòêè ïî çàäàííîìó çàêîíó

xx= ()z

íà ïîâåðõíîñòü âðàùåíèÿ ñ çàäàííîé ôîðìîé îáðàçóþùåé r(z)ìî-

æåò áûòü îöåíåíà ïî êðèòåðèþ (5.3) ïîñëå îïðåäåëåíèÿ òàíãåíñà

óãëà ãåîäåçè÷åñêîãî îòêëîíåíèÿ ïî ôîðìóëå (5.4).

Îòìåòèì, ÷òî òðàåêòîðèè óêëàäêè àðìèðóþùåé íèòè, ñîîòâåòñò

âóþùèå

|| ,tgq = const

ïðèíÿòî íàçûâàòü ëèíèÿìè ïîñòîÿííîãî îòêëî

íåíèÿ [8].

Î÷åâèäíî, ÷òî ñëó÷àþ

||tg

òð

q = k

ñîîòâåòñòâóåò òðàåêòîðèÿ, îò

êëîíÿþùàÿñÿ îò òðàåêòîðèè ãåîäåçè÷åñêîé íàìîòêè, â íàèáîëüøåé

ñòåïåíè îïðåäåëÿåìîé êîýôôèöèåíòîì òðåíèÿ

òð

Êîíêðåòèçèðóåì îñíîâíûå ïðîåêòíûå òðåáîâàíèÿ, ñôîðìóëèðî

âàííûå â îáùåì âèäå â íà÷àëå íàñòîÿùåãî ðàçäåëà.

Îïòèìàëüíîñòü ïðîåêòà îöåíèâàåòñÿ âåëè÷èíîé ìàññû îáîëî÷êè

áàëëîíà îïðåäåëÿåìîé ïî ôîðìóëå

mnfS=

,,r

(5.5)

ãäå ï—÷èñëî íèòåé, îáðàçóþùèõ ñèëîâóþ îáîëî÷êó; f—ïðèâåäåí

íàÿ ïëîùàäü ñå÷åíèÿ íèòè ñ ó÷åòîì ñâÿçóþùåãî;

— äëèíà íèòè

ìåæäó ïîëþñàìè;

— ïëîòíîñòü ìàòåðèàëà ñèëîâîé îáîëî÷êè.

88 Ãëàâà 5

Òåõíîëîãè÷åñêèå îãðàíè÷åíèÿ ñâîäÿòñÿ ê óñëîâèþ (5.3) è óñëî

âèþ íåïðåðûâíîñòè íèòè ïðè íàìîòêå (ïîñòîÿíñòâà ÷èñëà íèòåé,

ïðîõîäÿùèõ ÷åðåç ëþáîå ñå÷åíèå îáîëî÷êè), ìàòåìàòè÷åñêàÿ çàïèñü

êîòîðîãî èìååò âèä

nf = const. (5.6)

Óñëîâèå ñîõðàíåíèÿ ïðî÷íîñòè ôîðìóëèðóåòñÿ ñëåäóþùèì îá

ðàçîì:

max

() ,p ≤

(5.7)

ãäå

max

()p

— ìàêñèìàëüíûå íàïðÿæåíèÿ â àðìèðóþùèõ íèòÿõ, âîç

íèêàþùèå ïðè äåéñòâèè âíóòðåííåãî äàâëåíèÿ p;

— äîïóñêàåìûå

íàïðÿæåíèÿ.

Ïðîåêòíûì ïàðàìåòðîì â äàííîì ñëó÷àå ÿâëÿåòñÿ çàâèñèìîñòü

ôóíêöèè Êëåðî îò ïðîäîëüíîé êîîðäèíàòû

xj() ()sin ()zrz z=

, îäíî-

çíà÷íî îïðåäåëÿþùàÿ òðàåêòîðèþ íàìîòêè êîíñòðóêöèè.

Ïðè ïðîåêòèðîâàíèè áàëëîíà, èçãîòàâëèâàåìîãî íàìîòêîé îä-

íîíàïðàâëåííîé ëåíòû, áóäåì ïðåíåáðåãàòü íåñóùåé ñïîñîáíîñòüþ

ïîëèìåðíîãî ñâÿçóþùåãî, ñîåäèíÿþùåãî îòäåëüíûå íèòè â ëåíòå, è

çàìåíèì ëåíòó ñèñòåìîé íèòåé, âîñïðèíèìàþùèõ íàãðóçêó òîëüêî â

íàïðàâëåíèè àðìèðîâàíèÿ. Òàêîå óïðîùåíèå äîïóñòèìoe, ïîñêîëü-

êó ïðî÷íîñòü îäíîíàïðàâëåííîé ëåíòû ïîïåðeê àðìèðîâàíèÿ íà

1–2 ïîðÿäêà ìåíüøå, ÷åì â íàïðàâëåíèè àðìèðîâàíèÿ. Êðîìå òîãî,

ôèçè÷åñêàÿ êàðòèíà ðàáîòû êîíñòðóêöèè ïðè íàãðóçêàõ, áëèçêèõ ê

ðàçðóøàþùèì, êàê ïðàâèëî, ñîîòâåòñòâóåò íèòÿíîé ñèñòåìå, òàê êàê

ðàçðóøåíèå ñâÿçóþùåãî íàñòóïàåò ñóùåñòâåííî ðàíüøå èñ÷åðïàíèÿ

íåñóùåé ñïîñîáíîñòè îáîëî÷êè [9].

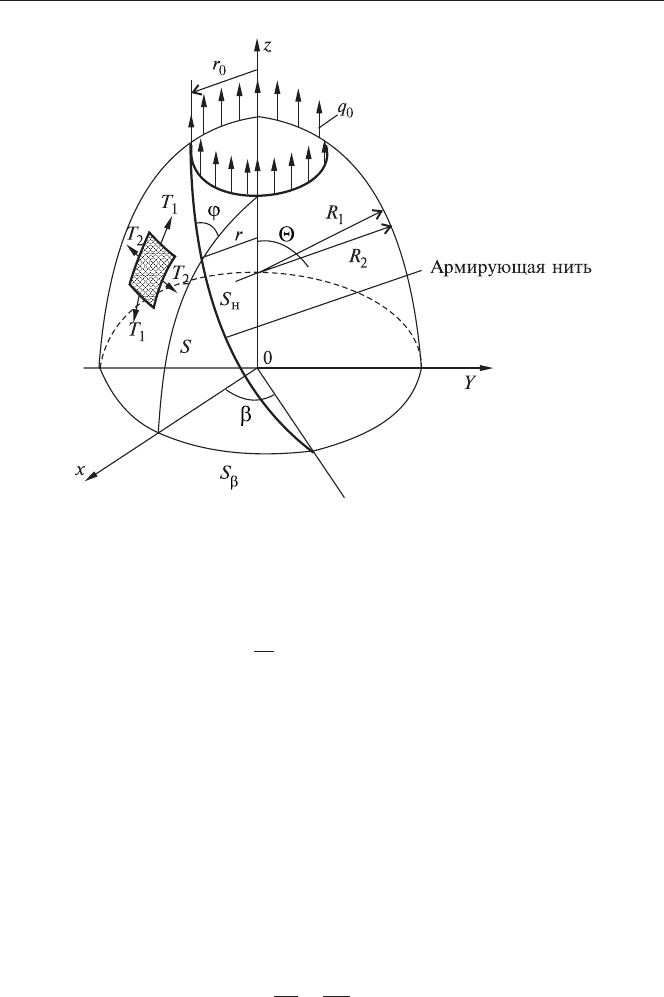
Óðàâíåíèÿ ðàâíîâåñèÿ áåçìîìåíòíîé îáîëî÷êè âðàùåíèÿ, íà

ãðóæåííîé âíóòðåííèì äàâëåíèåì ð, äëÿ ñëó÷àÿ îñåñèììåòðè÷íîãî

äåôîðìèðîâàíèÿ èìåþò âèä

rT T R

q() ,

121

0−=cos

(5.8)

Çäåñü T

, T

— èíòåíñèâíîñòè ìåðèäèîíàëüíûõ è êîëüöåâûõ óñèëèé,

âîçíèêàþùèõ â îáîëî÷êå; R

, R

— ãëàâíûå ðàäèóñû êðèâèçíû ïî

âåðõíîñòè âðàùåíèÿ (ðèñ. 5.2).

Èñïîëüçóÿ èçâåñòíîå ñîîòíîøåíèå [12]

Rddr

cos qq=

Ïðîåêòèðîâàíèå è ðàñ÷åò ñèëîâîé îáîëî÷êè êîðïóñà 89

ïåðâîå óðàâíåíèå ðàâíîâåñèÿ èç ñèñòåìû (5.8) ìîæíî çàïèñàòü â áî-

ëåå ïðîñòîé ôîðìå:

rT T() .

0−=

(5.9)

Ìåðèäèîíàëüíûå è êîëüöåâûå íàïðÿæåíèÿ â îáîëî÷êå

âûðàæàþòñÿ ÷åðåç íàïðÿæåíèÿ â àðìèðóþùèõ íèòÿõ

ñëåäóþùèì

îáðàçîì [9]:

ss j

= cos , ss j.

= sin

(5.10)

Ñîîòâåòñòâóþùèå âûðàæåíèÿ äëÿ ìåðèäèîíàëüíûõ è êîëüöåâûõ

ïîãîííûõ óñèëèé èìåþò âèä

Thh

==ssjcos , Thh

==ssjsin .

(5.11)

Çäåñü h — òîëùèíà îáîëî÷êè, îïðåäåëÿåìàÿ èç óñëîâèÿ íåïðåðûâíî

ñòè íàìîòêè (5.6) ïî ôîðìóëå

0+=.

(5.12)

90 Ãëàâà 5

Ðèñ. 5.2. Ãåîìåòðè÷åñêîå ïðåäñòàâëåíèå îáîëî÷êè âðàùåíèÿ è ðàñïîëîæåíèå

àðìèðóþùåé íèòè íà äíèùå ñîñóäà äàâëåíèÿ.