Вольдек А.И. Электрические машины
Подождите немного. Документ загружается.


Если при этом сохраним шаг по пазам Уи = 4, то у
г
= и
а
у
1г
=
= 2-4 = 8, у
2
— —7, у = у
к
= +1. Эта обмотка будет равносек-
циоиной.
Схему такой обмотки можно изображать двояким образом, как
показано на рис. 3-21, а и б. Верхний ряд цифр на этом рисунке
представляет собой номера секций, а нижний ряд — номера пазов.
Так как число пазов не изменилось, то и звезда пазовых э. д. с.
не изменяется (см. рис. 3-11, б). Векторы э. д. с. каждой пары сек-
ций (1—2, 3—4 и т. д.) будут совпадать по фазе, а векторы э. д. с.
секций, лежащих в соседних пазах (секции 2—3, 4—5 и т. д.), будут
\1\г\з\№
Рис. 3-22. Варианты изображения схемы ступенчатой обмотки с 2р
~-
Z = 18, и
п
= 2, Z
t
= S = К = 36, & = 9, у
2
= -8, у = у
к
=
= 4,
+
1
сдвинуты на 40°, как и в предыдущем случае. Поэтому многоуголь-
ник э, д. с. обмотки будет выглядеть так же, как и на рис. 3-19,
с тем лишь различием, что каждая сторона многоугольника будет
представлять собой сумму э. д. с. двух секций, лежащих в общих
пазах.
Если при тех же значениях 2р, Z и Z
a
выбрать шаги по элемен-
тарным пазам
й = ? =
9;
й-1-9 = -8,
то обмотка будет ступенчатой. Схема такой обмотки также может
быть изображена двояким образом, как показано на рис. 3-22, а и б.
При этом обмотка имеет два значения шага у
и
ло зубцам; у[
г
= 4
и y[z = 5.
Построим векторы э. д. с. секций Т, 2, 3 этой обмотки (рис. 3-23).
Секция ) лежит в пазах 1 и 5, и ее э. д. с. равна разности векторов 1
и 5 звезды на рис. 3-11, б. Построенный таким образом вектор сек-
ции 1 на рис. 3-23 обозначен 1, а составляющие его векторы пазов или
секционных сторон обозначены 1' и —5". Секция 2 лежит в пазах 1

и 6, а секция 3 — в пазах 2 и 6, и векторы э. д. с. этих секций по-
строены и обозначены на рис. 3-23 по такому же принципу, как
и вектор секции 1. Как следует из этого рисунка, векторы э. д. с.
секций сдвннуты относительно друг друга на 20
е
, т. е. на половину
угла, соответствующего пазовому делению.
1 v-j" -б"А2 Таким образом, ступенчатая обмотка с Z = 18
VV // 34 г и и Z
3
— 36 в этом отношении равноценна об-
мотке с удвоенным числом пазов Z = Z
3
= 36.
Соответственно этому многоугольник э. д. с.
ступенчатой обмотки будет иметь в два раза
больше сторон и в большей мере прибли-
жаться к окружности, чем при равносекцион-
ной обмотке. Это является некоторым пре-
имуществом ступенчатой обмотки. Однако
главное преимущество такой обмотки состоит
в улучшении условий коммутации (см. § 6-6).
Уравнители первого рода для рассмот-
ренных равносекциоиной и ступенчатой обмо-
ток выполняются так же просто, как и в ра-
нее рассмотренном случае. Разница заклю-
чается лишь в том, что вследствие удвоения S = К шаг уравни-
телей у
Ур
также удваивается.
Аналогично схемам на рис. 3-21 и 3-22 можно изображать та-
кже схемы и других типов обмоток при и
П
> 1.
§ 3-4. Сложная петлевая обмотка
Общие положения. Сложную, или многоходовую, петлевую
обмотку можно рассматривать как сочетание нескольких (пг — 2,
3...) простых петлевых обмоток. Такую обмотку называют также
сложной параллельной. В рассматриваемой обмотке секции и кол-
лекторные пластины m простых обмоток по окружности чередуются
и для отвода тока из обмотки необходимо, чтобы ширина щеток
была не меньше m коллекторных делений. Таким образом, m простых
обмоток m-ходовой обмотки включаются с помощью щеток парал-
лельно и количество параллельных ветвей сложной петлевой об-
мотки
2а = 2pm. (3-18)
Результирующий шаг по элементарным пазам и шаг по коллек-
тору сложной петлевой обмотки
О
Рис. 3-23. Векторы
э. д. с. секций обмот-
ки, показанной на
рис. 3-22
у = у
к
= ±т.
(3-19)

Шаги £/
г
и у
2
= у — ух определяются так же, как и для простой
петлевой обмотки.
Сложная петлевая обмотка применяется в мощных машинах
с большими токами якоря, и секции обмотки в этом случае являются
одновитковыми.
Симметричная двухходовая двукратнозамкнутая петлевая об-
мотка. Рассмотрим особенности сложной петлевой обмотки на кон-
кретном примере: m — 2, 2р = 4, Z = Z
b
— S = К = 20, и
а
— 1.
1-й ход 1'л Зк 5л 7к # ilk 13к $ Пк <
oSmmxu / V V V V V V V V V \
' 7 5" 1Г 1Г if /3" 1 J"
v
5
2-й ход
2
А f f
е
А
f f f f f
2
°k
o6mmu
w//////У *
Рис. 3-24. Таблица соединений секционных сторон
сложной петлевой обмотки, показанной на рис. 3-25
При этом 2а = 4 -2 = 8 и условия симметрии (3-5)—(3-7) соблю-
даются. Заметим, что эти условия в сложной петлевой обмотке при
m — 2 соблюдаются всегда, если Юр равно четному числу.
Выберем шаги обмотки:
9П
</
= </к = + 2; i/i = f+l =
6; #2
= 2
— 6 —
— 4.
По известным значениям шагов построим таблицу соединений
секционных сторон обмотки (рис. 3-24). При этом, начиная с пла-
стины и секции 1, обойдем все нечетные секции и вернемся к пла-
стине /, замкнув первый ход обмотки. Начав второй ход с пластины 2,
обойдем все четные секции и снова вернемся к пластине 2, замкнув
второй ход обмотки.
Таким образом, в рассматриваемом случае получаются две са-
мостоятельные обмотки, которые соединяются параллельно с по-
мощью щеток. Это обусловлено тем, что S = К является в данном
случае четным числом. Такая обмотка называется двукратнозамкну-
той. В общем случае кратность замыкания сложной петлевой об-
ыотки t равна общему наибольшему делителю чисел m и К..
Схема рассматриваемой обмотки представлена на рис. 3-25.
На рис. 3-26 изображена звезда э. д. с. пазов или сторон секций,
в которой векторы сдвинуты на угол
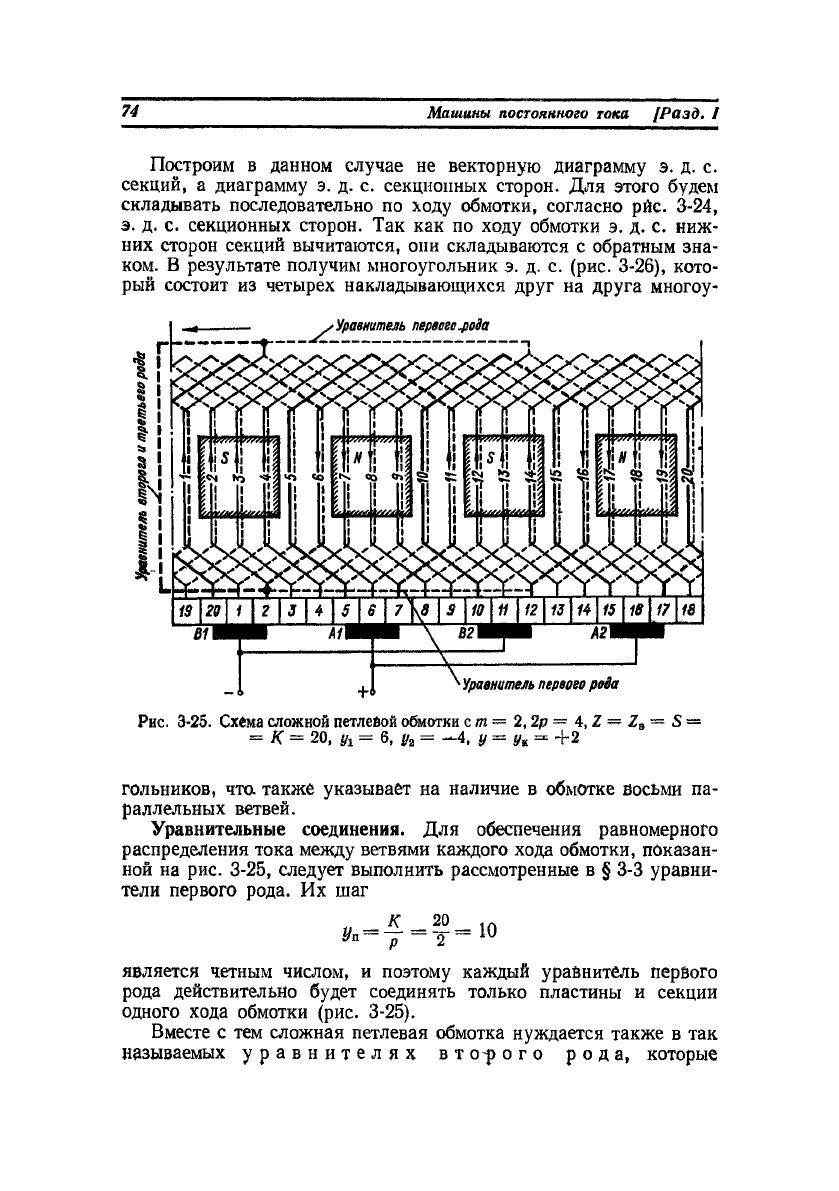
Построим в данном случае не векторную диаграмму э. д. с.
секций, а диаграмму э. д. с. секционных сторон. Для этого будем
складывать последовательно по ходу обмотки, согласно рйс. 3-24,
э. д. с. секционных сторон. Так как по ходу обмотки э. д. с. ниж-
них сторон секций вычитаются, они складываются с обратным зна-
ком. В результате получим многоугольник э. д. с. (рис. 3-26), кото-
рый состоит из четырех накладывающихся друг на друга многоу-
Рис. 3-25. Схема сложной петлейой обмотки с m = 2,2р = 4, 2 = Z
B
— S —
= К = 20, й = 6, й = -4, у = у
%
= +2
гольников, что также указывает на наличие в обмотке восьми па-
раллельных ветвей.
Уравнительные соединения. Для обеспечения равномерного
распределения тока между ветвями каждого хода обмотки, показан-
ной на рис. 3-25, следует выполнить рассмотренные в § 3-3 уравни-
тели первого рода. Их шаг
К 20
1Г1
2>п
= у =Т=
10
является четным числом, и поэтому каждый уравнитель первого
рода действительно будет соединять только пластины и секции
одного хода обмотки (рис. 3-25).
Вместе с тем сложная петлевая обмотка нуждается также в так
называемых уравнителях второго рода, которые
служат для выравнивания нагрузки между разными ходами сложной
обмотки.
Каждая щетка (рис. 3-25) касается пластин разных ходов об-
мотки. Щеточный контакт не может быть вполне устойчивым, так
как отдельные пластины несколько выступают по отношению к со-
седним и т. д. Поэтому условия контакта с пластинами разных
ходов постоянно изменяются, что вызывает беспрерывное перерас-
пределение тока нагрузки и пульсацию токов отдельных ходов об-
мотки. Вместе с тем сильно колеблются также напряжения между
соседними пластинами. Все это приводит к перегрузке отдельных
участков щеток, их искрению и т. д.
Во избежание таких явлений необходимо соединить теорети-
чески равнопотенциальные точки разных ходов обмотки уравни-
телями второго рода и таким образом осуществить их парал-
лельное соединение внутри самой обмотки помимо или до щеточ-
ного контакта.
Как уже указывалось, две равнопотенциальные точки рассмат-
риваемой обмотки удалены на одной стороне якоря на у
п
= 10 пла-
стин или элементарных пазов и принадлежат поэтому одному ходу
обмотки. Вследствие этого в данном случае выполнение уравни-
телей второго рода на одной стороне якоря невозможно.
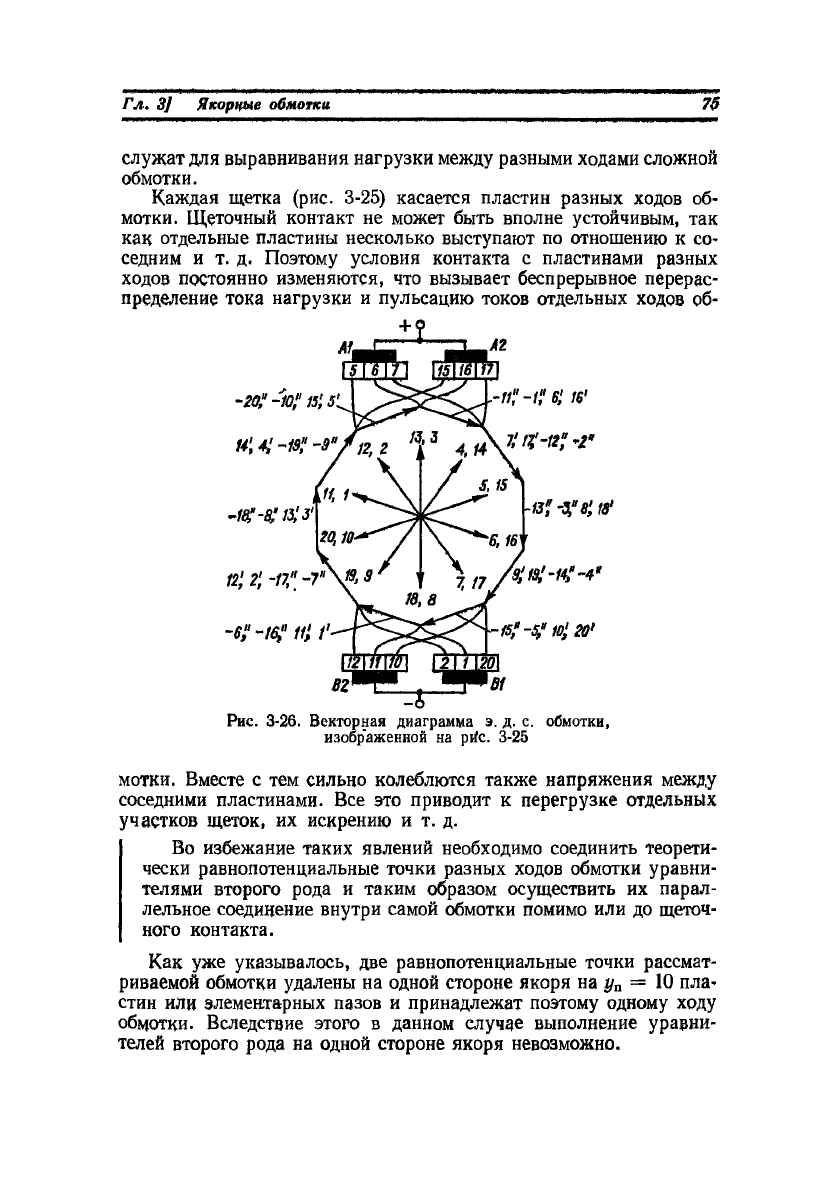
.-//,"-/,"(?; 16'
7,'ц'чг;'^"
$ ю;-и,"-4*
-а", -дч'
Рис. 3-26. Векторная диаграмма э. д. с. обмотки,
изображенной на prfc. 3-25

Из рассмотрения рис. 3-26 видно, что две равнопотенциальные
точки разных ходов обмотки будут, например, соответствовать
концу вектора Г (или началу вектора — 7") и началу вектора 2'.
Это будут соответственно середина лобовой части секции 1 на сто-
роне, противоположной коллектору, и коллекторная пластина 2.
Эти две равнопотенциальные точки (рис. 3-25), а также другие ана-
логичные пары точек можно соединить уравнителями второго рода,
проходящими между сердечником якоря и валом машины. В данном
случае уравнители первого рода, принадлежащие разным ходам
обмотки, выполняются на разных сторонах якоря, как показано на
рис. 3-25, так как при этом р уравнителей второго рода можно
заменить одним. Например, показанный на рис. 3-25 уравнитель
второго рода для секций / и 2 служит также уравнителем второго
рода для середины секции 11 и начала секции 12. В таком случае
обычно выполняют только один уравнитель второго рода на (2 .-4-
3) р коллекторных пластин. Недостатком уравнителей, прохо-
дящих между сердечником якоря и валом, является их конструк-
тивная сложность.
Иногда в машинах с тяжелыми условиями коммутации в двух-
ходовых петлевых обмотках применяют также уравнители
третьего рода. Их задача сводится к тому, чтобы при вра-
щении коллектора щетка замыкала накоротко не сразу всю сек-
цию, а сначала одну ее половину и затем другую.
Для этого необходимо середину одновитковой секции, располо-
женной на противоположной от коллектора стороне якоря, соеди-
нить с коллекторной пластиной, находящейся между началом и
концом данной секции. В обмотке, показанной на рис. 3-25, такую
роль выполняют уравнители второго роДа, т. е. они являются также
одновременно уравнителями третьего рода. Как видно из рис. 3-25,
при движении коллектора вправо щетка В1 сначала замкнет пла-
стины 1—2 и тем самым левую половину секции 1, а затем пластины
2—3 и тем самым правую половину секции 1.
Уравнители третьего рода выполняют в таком количестве, чтобы
коммутация всей обмотки происходила по полусекциям. Естественно,
Что уравнители третьего рода можно выполнять лишь в том
случае, если соединяемые ими точки обмотки имеют равные по-
тенциалы.
Несимметричные сложные петлевые обмотки. Рассмотрим двух-
ходовую петлевую обмотку со следующими данными: m — 2, 2р =
= 4, 2а = 8, Z = Z
9
= S = К = 18, у = у
к
= +2, у
г
= 4, у
2
=
= —2. Так как К — четное число, обмотка будет двукратнозамкну-
той. Однако она не будет симметричной, так как условия (3-5) и
(3-6) не выполняются. Заметим, что при m = 2 эти условия не вы-
полняются, если /С/р равно нечетному числу.

Последовательность соединений секций в этой обмотке предста-
влена на рис. 3-27, а схема обмотки — на рис. 3-28.
Звезда э. д. с. секций и диаграмма э. д. с. рассматриваемой об-
мотки, построенные на основании рис. 3-27 и 3-28, изображены
на рис. 3-29. При этом масштаб звезды э. д. с. в два раза меньше
масштаба многоугольника э. д. с. То обстоятельство, что много-
угольники э. д. с. на рис. 3-29 не совмещаются, также свидетель-
ствует о несимметрии обмотки.
Равнопотенциальные точки этой обмотки имеют шаг
и =— =
—
= 9
Уп
р
2 '
что следует также из рис. 3-29. Эти точки принадлежат разным
ходам обмотки, и поэтому при соединении их получим уравнители
второго рода, которые
в данном случае распо-
}
.
йШ
пп* w
у
,
д
,
13
,
f5
,
лагаются на одной сто-
oSmmu
\
Ai А А А А А А А /
роне якоря (рис. 3-28).
ammKK
/ У./
д
У „У ,/,/,/ /
Но эти уравнители сое- 7 w
я
, г-тп , , , ,
диняют также парал-
2-й ход
A A A ?jAi А А А /
лельные ветви, находя- обмотка / у у У у » у у у
щиеся под разными па- 6 8 Ю t2
L
u_, К № 2
рами полюсов, И поэтому Рис. 3-27. Таблица соединений секционных сто-
одновременно являются Р°Н сложной петлевой обмотки, изображенной
также уравнителями
на
Р
ис
-
3-28
первого рода. То обстоя-
тельство, что эти ветви принадлежат разным ходам обмотки, не имеет
значения, так как при достаточном количестве уравнителей все
ветви, расположенные под разными полюсами, окажутся взаимно
соединенными друг с другом и щетки будут загружаться равномерно.
Простота выполнения уравнителей первого и второго рода яв-
ляется большим преимуществом рассматриваемой обмотки, и поэ-
тому несимметричные двухходовые обмотки с К/р, равным нечет-
ному числу, на практике часто предпочитают симметричным с К/р,
равным четному числу.
Предположим, что в обмотке, показанной на рис. 3-28, жела-
тельно выполнить также уравнители третьего рода, один из которых
можно было бы провести между точками а и б на рис. 3-28. На
рис. 3-30, а построен вектор э. д. с. секции 1 этой обмотки, а на
рис. 3-29 э. д. с. секции. 1 представлена штриховой линией также
в виде разности э. д. с. проводников витка. При этом из рис. 3-29
видно, что точки а и б на рис. 3-28 не являются равно потенциаль-
ными и выполнить уравнители третьего рода невозможно. Если бы
на схеме рис. 3-28 был взят удлиненный шаг у
1
= 5, то потенциал
точки а сместился бы в противоположную сторону (рис. 3-30, б).
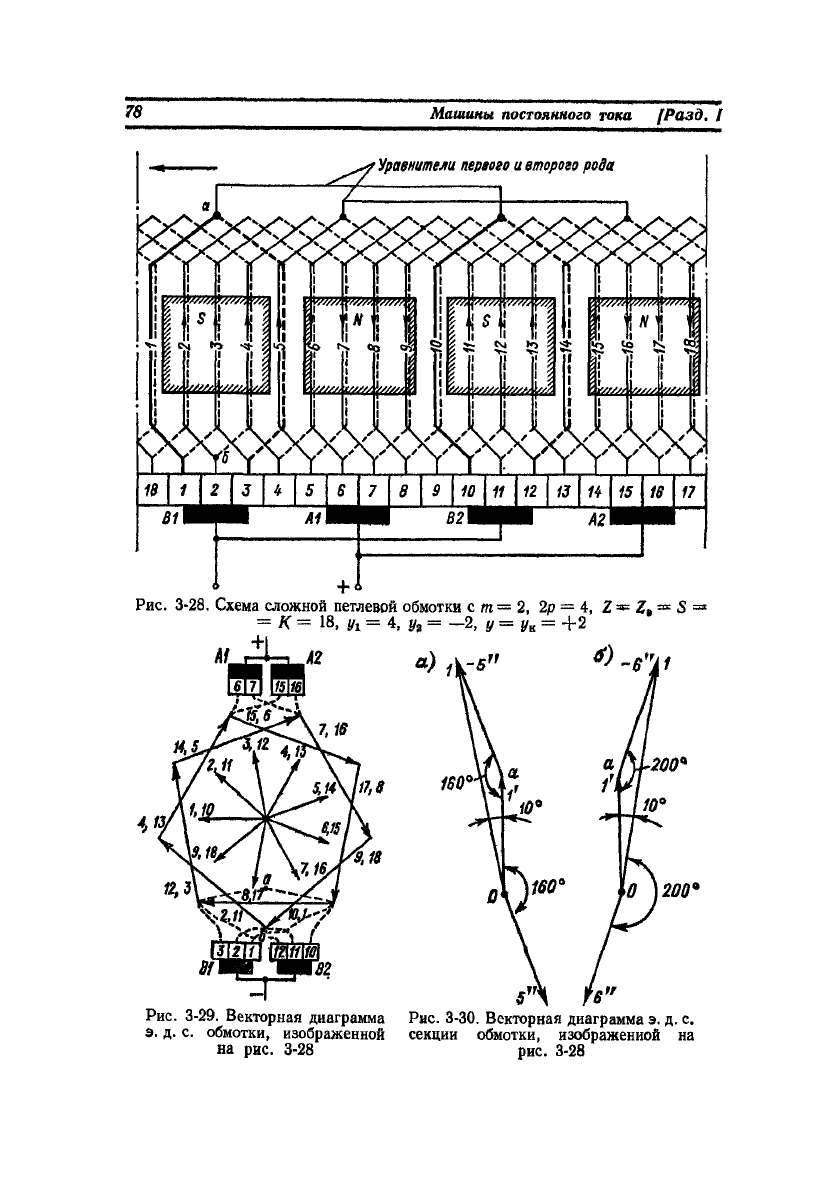
I'
-f. I,
Рис. 3-28. Схема сложной петлевой обмотки с т= 2, 2р — 4, Z, = S =
= К = 18, y
t
= 4, у
%
= -2, y=y
s
= +2
Рис. 3-29. Векторная диаграмма Рис. 3-30. Векторная диаграмма э. д. с.
э. д. с. обмотки, изображенной секции обмотки, изображенной на
на рис. 3-28 рис. 3-28

Гл. 3J Якорные обмотки
79
Однако и в этом случае точки а и б были бы неравнопотенциальными.
Поэтому при необходимости выполнения уравнителей третьего
рода применяют симметричные двухходовые обмотки типа пока-
занной на рис. 3-25 с К 1р, равным четному числу.
При нечетном К двухходовая петлевая обмотка будет однократ-
нозамкнутой, но такая обмотка будет во всех случаях несимметрич-
ной, так как а = 2р является четным числом и условие (3-5) не
выполняется. Трехходовые петлевые обмотки (пг = 3, а = 3р)
будут тоже всегда несимметричными, так как не выполняется усло-
вие (3-7). Тем не менее в последнее время обмотки с m = 3 исполь-
зуются в мощных машинах.
Для несимметричных обмоток всегда требуется анализ возмож-
ности их применения. Эти вопросы, а также особенности выполне-
ния многоходовых обмоток с и
п
> 1 и ступенчатых обмоток рас-
сматриваются в специальных руководствах [12, 30, 40, 41].
§ 3-5. Простая волновая обмотка
Общие положения. Мысленно
ненные секции простой волновой
разный обход якоря, причем
каждый обход включает р сек-
ций и заканчивается на коллек-
торной пластине, которая нахо-
дится слева или справа рядом
с исходной (рис. 3-31). В первом
случае (рис. 3-31, а) получается
неперекрещенная обмотка, а во
втором (рис. 3-31, б) —пере-
крещенная. Во втором случае
расход меди будет несколько
больше. Рассматриваемую об-
мотку называют также про-
стой последовательной обмот-
кой.
В соответствии со сказанным
обходя последовательно соеди-
обмотки, мы совершаем волнооб-
/V
ч
t
б) rtS У
г
|
У
fijl ft ft
Рис. 3-31. Секции неперекрещенной (a)
и перекрещенной (б) простой волновой
обмотки
между шагом по 'коллектору у
к
(рис. 3-31) и количеством коллекторных пластин К простой волно-
вой обмотки существует зависимость
ру
х
±
1
= К,
откуда
К+ 1
(3-20)

Знак минус относится к неперекрещенной обмотке, а знак
плюс — к перекрещенной. Поскольку шаг у* — у должен быть
целым числом, то К не может принимать произвольных значений.
Шаг у
г
определяется по формуле (3-9), и
уг = у-ух-
(3-21)
Шаги Ух и у
2
близки к т, а у = у
к
— к 2т.
Симметричная волновая обмотка. Ознакомимся со свойствами
простой волновой обмотки на примере обмотки с 2р = 4 и Z = Z
3
=
= S = К = 17. Возьмем при этом
Ук =
У-
К-1
17-1
:8
Z=> 17 1 .
г/2
= г/-«/1 = 8-4 = 4.
Порядок соединений секционных сторон обмотки определяется
таблицей на рис. 3-32, а схема обмотки имеет вид, показанный на
>Т 8[ 161 71 151 6'
k
[»
А
' € 12[ t it 2i[f0l
.. I
4
/
4
'/
4
/ \
LJ-J^a * v
\J \J \ J \ i / \ / \\J \J \ / \ / \ / \ / \y ч
3
У
Jf
y 17 16* 7 №
Рис. 3-32. Таблица соединений секционных сторон простой волновой
обмотки, показанной на рис. 3-33
рис. 3-33. Ряд секций, выделенных на рис. 3-33 жирными линиями,
в отличие от секций петлевых обмоток замыкается накоротко через
две щетки одной полярности и соединительные провода между ними.
Короткозамкнутые секции обведены рамкой также и на рис. 3-32.
На рис. 3-34 построена звезда э. д. с. секций и векторная
диаграмма э. д. с. обмотки, представленной на рис. 3-33. Мас-
штаб звезды э. д. с. в два раза больше масштаба многоуголь-
ника э. д. с.
Как следует из рис. 3-32, 3-33 и 3-34, обмотка имеет две парал-
лельные ветви. Одна из них содержит секции 17, 8, 16, 7, 15, 6,
присоединена своими концами к коллекторным пластинам 17, 14
и расположена, таким образом, между щетками А2, В2. Другая
ветвь содержит секции 13, 4, 12, 3, 11, 2, присоединена концами
к пластинам 13, 10 и расположена между щетками В2, А1,
