Вольдек А.И. Электрические машины

Подождите немного. Документ загружается.

основной характеристики машины, а также по расчетным данным.

Рассмотрим здесь его построение с помощью х. х. х. и х. к. з.,

для чего обратимся к рис. 9-5,ч где изображены х. к. з. / = } (i

)

(прямая 1) и начальная, прямолинейная, часть х. х.~х. U = f (i

)

(прямая 2), проходящие через начало координат.

Построим характеристический треугольник для номинального

тока машины /

= / = /

, которому на х. к. з. соответствует

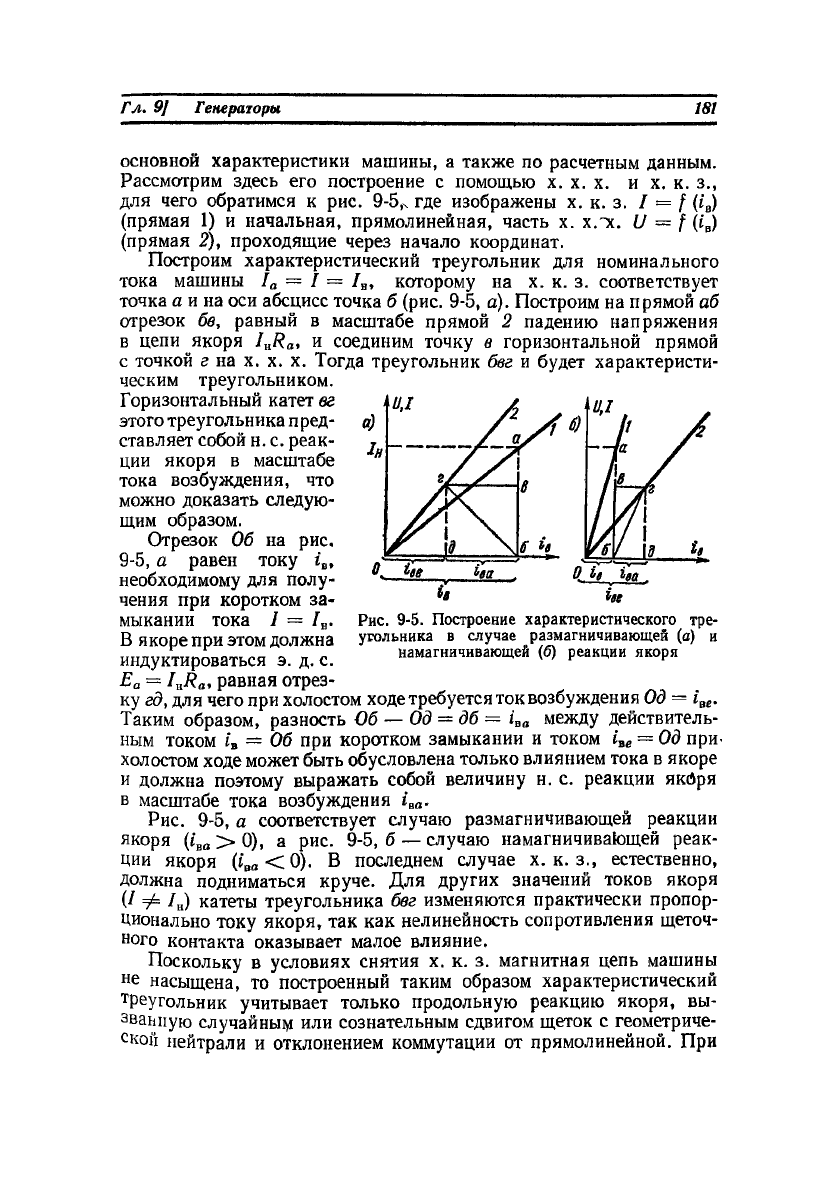
точка а и на оси абсцисс точка б (рис. 9-5, а). Построим на прямой аб

отрезок бв, равный в масштабе прямой 2 падению напряжения

в цепи якоря /

/?о> и соединим точку в горизонтальной прямой

с точкой г на х. х. х. Тогда треугольник бег и будет характеристи-

ческим треугольником.

Горизонтальный катет вг

этого треугольника пред-

ставляет собой н. с. реак-

ции якоря в масштабе

тока возбуждения, что

можно доказать следую-

щим образом.

Отрезок Об на рис,

9-5, а равен току i

необходимому для полу-

чения при коротком за-

мыкании тока / = /

В якоре при этом должна

индуктироваться э. д. с.

= Л,Ra, равная отрез-

ку гд, для чего при холостом ходе требуется ток возбуждения Од = г

ве

Таким образом, разность Об — Од = дб = i

между действитель-

ным током г"

= Об при коротком замыкании и током i

= Од при-

холостом ходе может быть обусловлена только влиянием тока в якоре

и должна поэтому выражать собой величину н. с. реакции якйря

в масштабе тока возбуждения t

Рис. 9-5, а соответствует случаю размагничивающей реакции

якоря (i

> 0), а рис. 9-5, б — случаю намагничивающей реак-

ции якоря (t

< 0). В последнем случае х. к. з., естественно,

Должна подниматься круче. Для других значений токов якоря

(I Ф /

) катеты треугольника бег изменяются практически пропор-

ционально току якоря, так как нелинейность сопротивления щеточ-

ного контакта оказывает малое влияние.

Поскольку в условиях снятия х. к. з. магнитная цепь машины

не насыщена, то построенный таким образом характеристический

треугольник учитывает только продольную реакцию якоря, вы-

званную случайны^ или сознательным сдвигом щеток с геометриче-

ской нейтрали и отклонением коммутации от прямолинейной. При

Рис. 9-5. Построение характеристического тре-

угольника в случае размагничивающей (а) и

намагничивающей (6) реакции якоря

установке щеток на геометрической нейтрали катет треугольника

= дб равен н. с. коммутационной реакции якоря (в масштабе г

)

и характеризует качество коммутации (на рис. 9-5, а — замедлен-

ная коммутация и на рис. 9-5, б — ускоренная). Когда щетки

стоят на нейтрали и коммутация прямолинейна, г

во

•= дб = 0 и

треугольник бег вырождается в вертикальную прямую.

Для построения характеристического треугольника с учетом

влияния поперечной реакции якоря, можно воспользоваться ха-

рактеристикой холостого хода и внешней, регулировочной или на-

грузочной характеристикой. Обычно пользуются нагрузочной.

Внешняя характеристика генератора независимого возбужде-

ния U = f (/) при г'

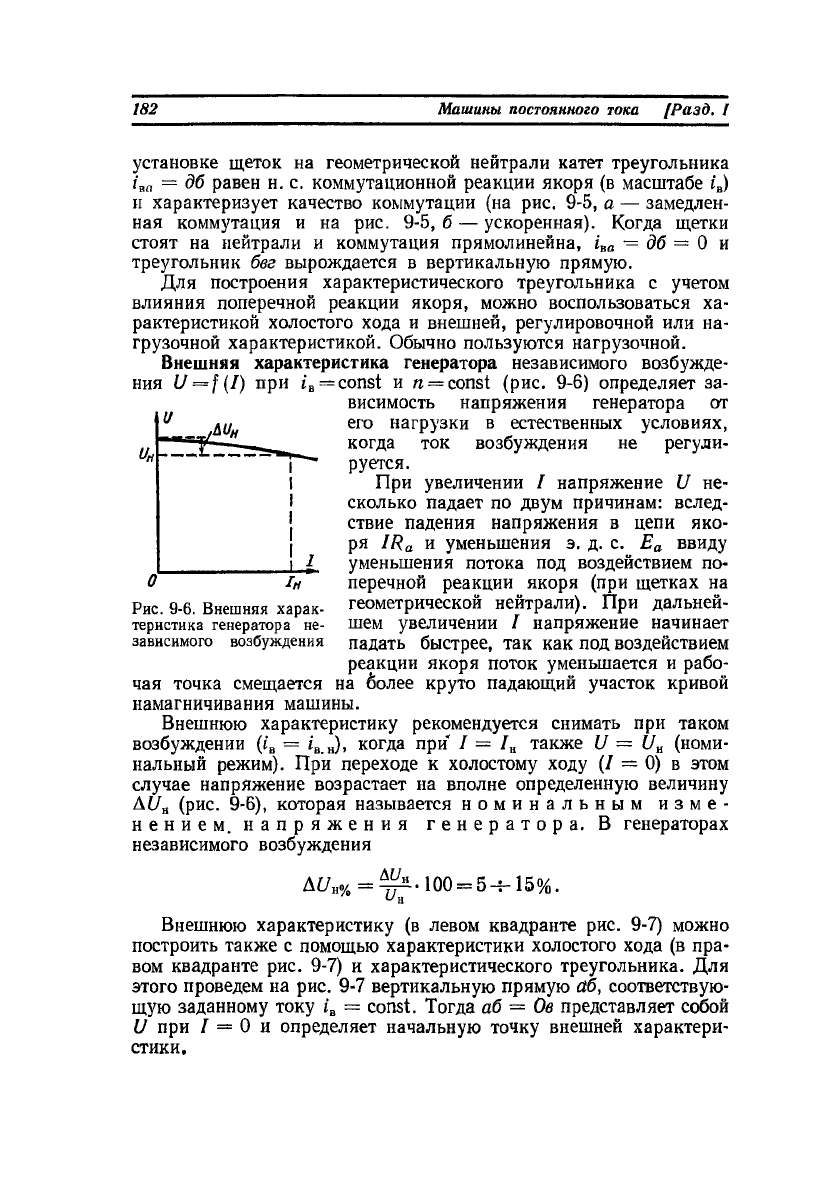
= const и га = const (рис. 9-6) определяет за-

висимость напряжения генератора от

его нагрузки в естественных условиях,

когда ток возбуждения не регули-

руется.

При увеличении I напряжение U не-

сколько падает по двум причинам: вслед-

ствие падения напряжения в цепи яко-

ря IR

и уменьшения э. д. с. Е

ввиду

уменьшения потока под воздействием по-

перечной реакции якоря (при щетках на

геометрической нейтрали). При дальней-

шем увеличении / напряжение начинает

падать быстрее, так как под воздействием

реакции якоря поток уменьшается и рабо-

чая точка смещается на более круто падающий участок кривой

намагничивания машины.

Внешнюю характеристику рекомендуется снимать при таком

возбуждении (t'

= г

в н

), когда при / = /

также U = 1/

(номи-

нальный режим). При переходе к холостому ходу (/ = 0) в этом

случае напряжение возрастает на вполне определенную величину

A£/„ (рис. 9-6), которая называется номинальным изме-

нением. напряжения генератора. В генераторах

независимого возбуждения

Д£/

% = ^».Ю0 = 5Ч-15%.

Внешнюю характеристику (в левом квадранте рис. 9-7) можно

построить также с помощью характеристики холостого хода (в пра-

вом квадранте рис. 9-7) и характеристического треугольника. Для

этого проведем на рис. 9-7 вертикальную прямую йб, соответствую-

щую заданному току г

= const. Тогда аб = Ов представляет собой

U при / = 0 и определяет начальную точку внешней характери-

стики.

О I,„

Рис. 9-6. Внешняя харак-

теристика генератора не-

зависимого возбуждения

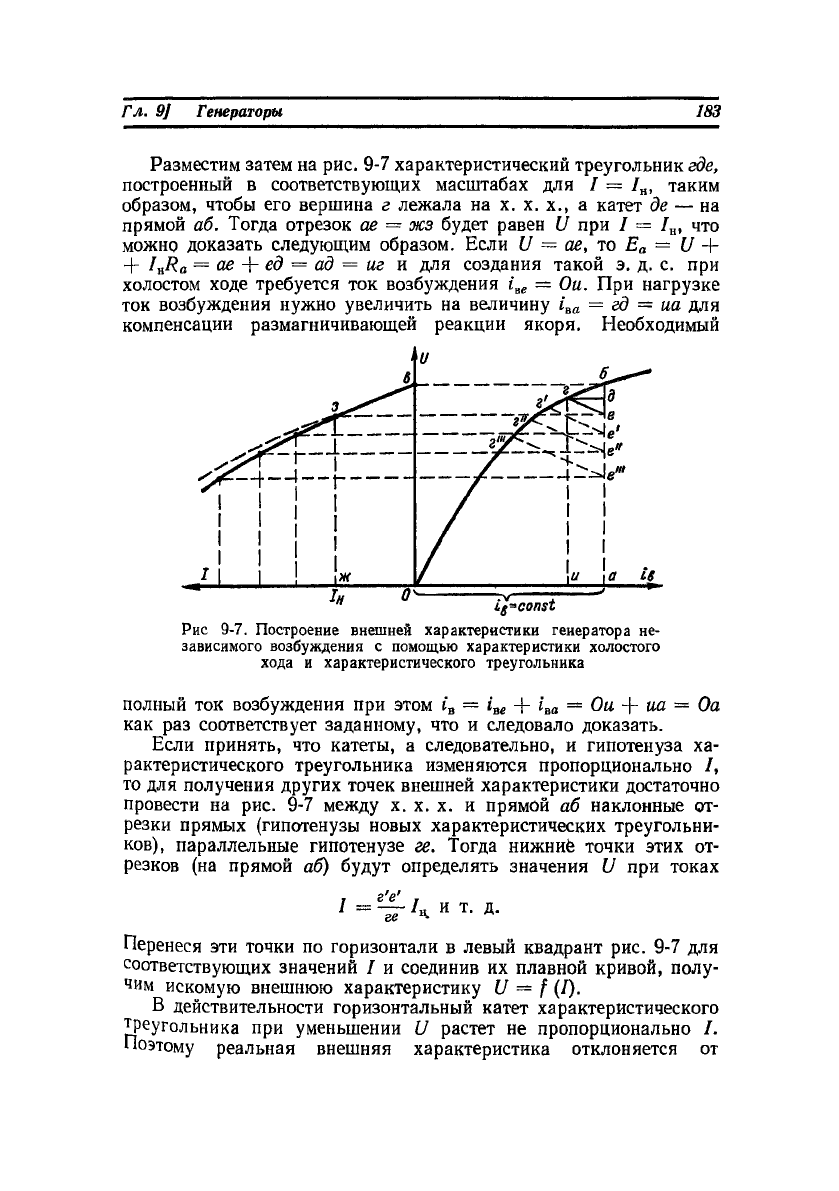
Разместим затем на рис. 9-7 характеристический треугольник где,

построенный в соответствующих масштабах для I = /

, таким

образом, чтобы его вершина г лежала на х. х. х., а катет де — на

прямой аб. Тогда отрезок ае = жз будет равен U при I = /

, что

можно доказать следующим образом. Если U = ае, то Е

= U +

+ /А = ае + ед = ад = иг и для создания такой э. д. с. при

холостом ходе требуется ток возбуждения i

— Ои. При нагрузке

ток возбуждения нужно увеличить на величину i

— гд = ua для

компенсации размагничивающей реакции якоря. Необходимый

Рис 9-7. Построение внешней характеристики генератора не-

зависимого возбуждения с помощью характеристики холостого

хода и характеристического треугольника

полный ток возбуждения при этом i

= i

+ i

= Ои + ua = Оа

как раз соответствует заданному, что и следовало доказать.

Если принять, что катеты, а следовательно, и гипотенуза ха-

рактеристического треугольника изменяются пропорционально I,

то для получения других точек внешней характеристики достаточно

провести на рис. 9-7 между х. х. х. и прямой аб наклонные от-

резки прямых (гипотенузы новых характеристических треугольни-

ков), параллельные гипотенузе ге. Тогда нижниё точки этих от-

резков (на прямой аб) будут определять значения U при токах

Перенеся эти точки по горизонтали в левый квадрант рис. 9-7 для

соответствующих значений I и соединив их плавной кривой, полу-

чим искомую внешнюю характеристику U — f (/).

В действительности горизонтальный катет характеристического

треугольника при уменьшении U растет не пропорционально I.

Поэтому реальная внешняя характеристика отклоняется от

построенной несколько в сторону, как показано в левом квадранте

рис. 9-7 штриховой линией.

Точка внешней характеристики с U = 0 определяет величину

тока короткого замыкания машины при полном возбуждении.

Так как Р

мало, то этот ток в 5—15 раз превышает /

. Такое корот-

кое замыкание весьма опасно, так как возникает круговой огонь,

а также большие механические усилия и моменты вращения. Поэтому

в условиях эксплуатации генераторы и двигатели средней и боль-

шой мощности защищаются быстродействующими автоматическими

выключателями в цепи якоря, которые ограничивают длительность

короткого замыкания и отключают машину от сети в течение 0,01—

0,05 сек после начала внезапного короткого

замыкания. Однако эти выключатели не за-

щищают машину при коротком замыкании

внутри машины.

Если имеются опытные х. х. х. и внешняя

характеристика и если известно R

, то,

производя построение на рис. 9-7 в обратной

последовательности, можно получить харак-

теристические треугольники с учетом реаль-

ных условий насыщения для любых значений

U и Е

Регулировочная характеристика i

= f (/)

при U = const и п — const показывает, как

нужно регулировать ток возбуждения, чтобы

при изменении нагрузки напряжение генера-

тора не менялось (рис. 9-8). С увеличением I ток г„ необходимо

несколько увеличивать, чтобш компенсировать влияние падени,я

напряжения I

и реакции якоря.

При переходе от холостого хода с U = U„ к номинальной на-

грузке / = /

увеличение тока возбуждения составляет 15—25%.

Построение регулировочной характеристики (нижний квадрант

рис. 9-9) по х. х. х. (верхний квадрант рис. 9-9) и характеристиче-

скому треугольнику производится следующим образом. Для задан-

ного U = Оа = вб = const величина t„ при / =

определяется

точкой в. Характеристический треугольник где для номинального

тока расположим так, чтобы его вершины г и е находились соответ-

ственно на х. х. х. и прямой абе. Тогда отрезок

Ож

— ае определяет

значение i

при I = /

, что можно доказать аналогично тому, как

это делалось в случае построения внешней характеристики. Для

получения других точек характеристики достаточно провести

между кривой х. х. х. и прямой абе на рис. 9-9 отрезки прямых,

параллельные гипотенузе ге. Тогда нижние концы (точки) этих

отрезков будут соответствовать величинам г

для значений /.опреде-

ляемых отношениями длин этих отрезков к гипотенузе ге, как и в пре-

Рис. 9-8. Регулировоч-

ная характеристика ге-

нератора независимого

возбуждения

дыдущем случае. Снеся эти точки вертикально вниз, в нижний

квадрант рис. 9-9, на уровень соответствующих значений /, получим

точки регулировочной характеристи-

ки. С учетом изменяющихся условий

насыщения реальная опытная регули-

ровочная характеристика будет иметь

вид, показанный в нижнем квадранте

рис. 9-9 штриховой линией.

Обратным построением, если даны

х. х. х. и регулировочная характери-

стика, можно получить характери-

стический треугольник.

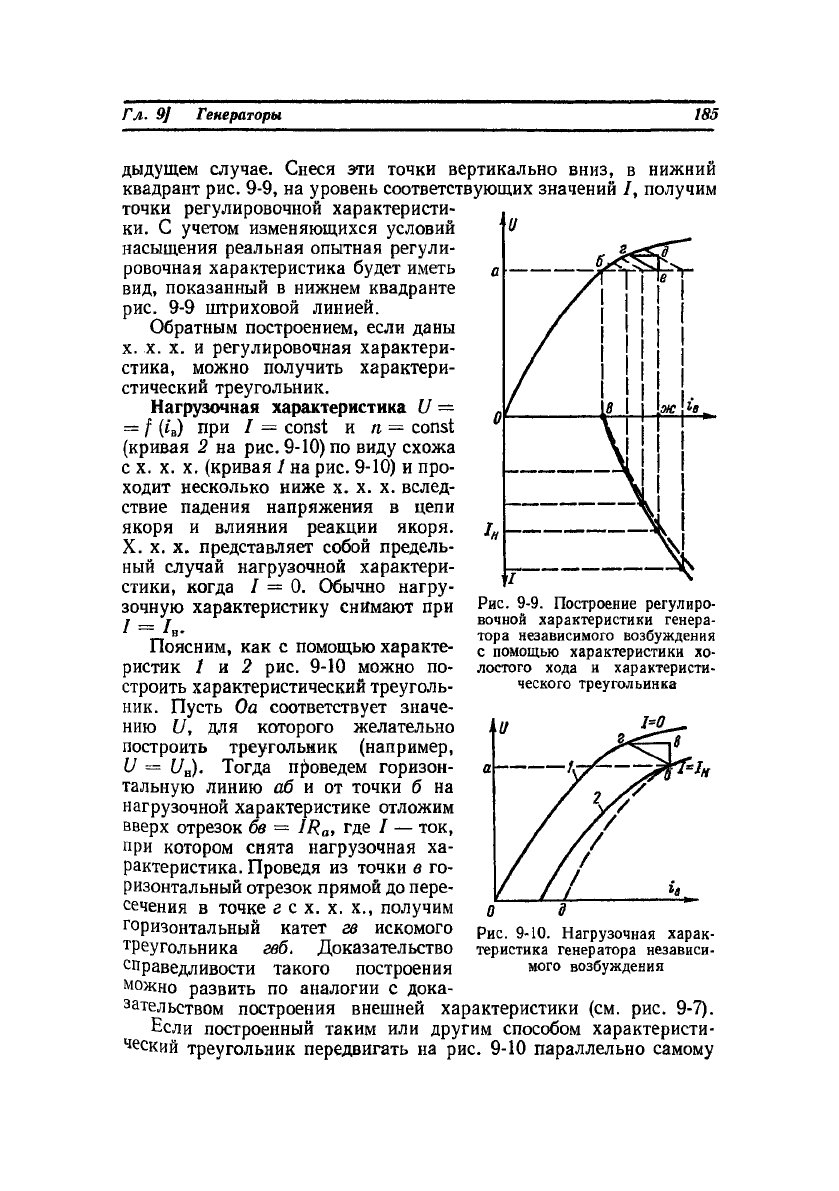
Нагрузочная характеристика U —

— f (г'

) при I — const и п = const

(кривая 2 на рис. 9-10) по виду схожа

с х. х. х. (кривая

на рис. 9-10) и про-

ходит несколько ниже х. х. х. вслед-

ствие падения напряжения в цепи

якоря и влияния реакции якоря.

X. х. х. представляет собой предель-

ный случай нагрузочной характери-

стики, когда / = 0. Обычно нагру-

зочную характеристику снимают при

I = /

Поясним, как с помощью характе-

ристик 1 и 2 рис. 9-10 можно по-

строить характеристический треуголь-

ник. Пусть Оа соответствует значе-

нию U, для которого желательно

построить треугольник (например,

U = U

). Тогда проведем горизон-

тальную линию аб и от точки б на

нагрузочной характеристике отложим

вверх отрезок бв = IR

, где I — ток,

при котором снята нагрузочная ха-

рактеристика. Проведя из точки в го-

ризонтальный отрезок прямой до пере-

сечения в точке г с х. х. х., получим

горизонтальный катет гв искомого

треугольника гвб. Доказательство

справедливости такого построения

можно развить по аналогии с дока-

зательством построения внешней характеристики (см. рис. 9-7).

Если построенный таким или другим способом характеристи-

ческий треугольник передвигать на рис. 9-10 параллельно самому

Рис. 9-9. Построение регулиро-

вочной характеристики генера-

тора независимого возбуждения

с помощью характеристики хо-

лостого хода и характеристи-

ческого треугольника

Рис. 9-10. Нагрузочная харак-

теристика генератора независи-

мого возбуждения

себе так, чтобы его вершина г скользила по х. х. х., то его вер-

шина б очертит нагрузочную характеристику (штриховая кривая

на рис. 9-10). Эта характеристика несколько разойдется с опытной

характеристикой 2, так как величина катета гв будет меняться

вследствие изменения условий насыщения.

Точка д на рис 9-10 соответствует короткому замыканию генера-

тора.

Все характеристики генераторов можно изобразить как в абсо-

лютных величинах, так и в относительных единицах. В последнем

случае характеристики будут более на-

I глядными. Характеристики однотипных

машин, хотя бы и разной мощности, по-

строенные в относительны х единицах, мало

отличаютс я друг от друга.

Влияние сдвига щеток с геометрической

нейтрали сказывается в том, что возни-

кает продольная реакция якоря, изме-

няющая поток полюсов, и поток добавоч-

ных полюсов будет индуктировать э. д. с.

не в коммутируемых секциях, а в рабочих

секциях параллельных ветвей якоря. При

повороте щеток против направления вра-

щения якоря (рис. 9-11) это вызовет уве-

а при сдвиге по направлению вращения —

уменьшение э. д. с. В первом случае внешняя характеристика

(см. рис. 9-6) с увеличением I будет падать медленнее или даже

может подниматься, во втором — будет падать более круто. При

наличии добавочных полюсов в обоих случаях возникает расстрой-

ство коммутации.

Влияние сдвига щеток на другие характеристики нетрудно ана-

лизировать подобным же образом.

Рис. 9-11. Сдвиг щеток

с нейтрали при наличии

добавочных полюсов

личение э. д. с. якоря,

§ 9-4. Генераторы параллельного возбуждения

Самовозбуждение генератора параллельного возбуждения про-

исходит при соблюдении следующих условий: 1) наличия остаточ-

ного магнитного потока полюсов; 2) правильного подключения

концов обмотки возбуждения или правильного направления вра-

щения. Кроме того, сопротивление цепи возбуждения R

при

данной скорости вращения ti должно быть ниже некоторого кри-

тического значения или скорость вращения при данном /?„

должна быть выше некоторой критической величины.

Для самовозбуждения достаточно, чтобы остаточный поток состав-

лял 2—3% от номинального. Остаточный поток такой величины

практически всегда имеется в уже работавшей машине. Вновь

изготовленную машину или машину, которая по каким-либо причи-

нам размагнитилась, необходимо намагнитить, пропуская через

обмотку возбуждения ток от постороннего источника.

При соблюдении необходимых условий процесс самовозбуждения

протекает следующим образом. Небольшая э. д. е., индуктируемая

в якоре остаточным магнитным потоком, вызывает в обмотке воз-

буждения малый ток i

. Этот ток вызывает увеличение потока

полюсов, а следовательно увеличение э. д. е., которая в свою

очередь обусловливает дальнейшее увеличение г

, и т. д. Такой

лавинообразный процесс самовозбуждения продолжается до тех пор,

пока напряжение генератора

не

достигнет установившегося значения.

Если подключение концов обмотки возбуждения или направле-

ние вращения неправильны, то возникает ток i

обратного направ-

ления, вызывающий ослабление остаточного потока и уменьшение

э. д. е., вследствие чего самовозбуждение невозможно. Тогда необ-

ходимо переключить концы обмотки возбуждения или изменить

направление вращения. В соблюдении этих условий можно убе-

диться, следя с помощью вольтметра с малым пределом измерения

за напряжением якоря при замыкании и размыкании цепи возбуж-

дения.

Полярность зажимов генератора при самовозбуждении опреде-

ляется полярностью остаточного потока. Если при заданном направ-

лении вращения полярность генератора необходимо изменить,

то следует перемагнитить машину путем подачи тока в обмотку

возбуждения от постороннего источника.

Рассмотрим подробнее процесс самовозбуждения при холостом

ходе.

На рис. 9-12, а кривая 1 представляет собой х. х. х., а прямая 2 —

так называемую характеристику цепи возбуждения или зависи-

мость U

= R

, где R

= const — сопротивление цепи возбуж-

дения, включая сопротивление регулировочного реостата.

В процессе самовозбуждения i

Ф const и напряжение на концах

цепи возбуждения

л _ц> , d

)

. d

)

— + ——

где L

— индуктивность цепи возбуждения.

Напряжение якоря при холостом ходе (I = 0)

—

изображается на рис. 9-12, а кривой 1. Так как £„ мало, то практи-

чески U

= Е

Но в генераторе параллельного возбуждения (см. рис. 9-1, б)

^а = U

. Поэтому разность ординат кривой / и прямой 2 на

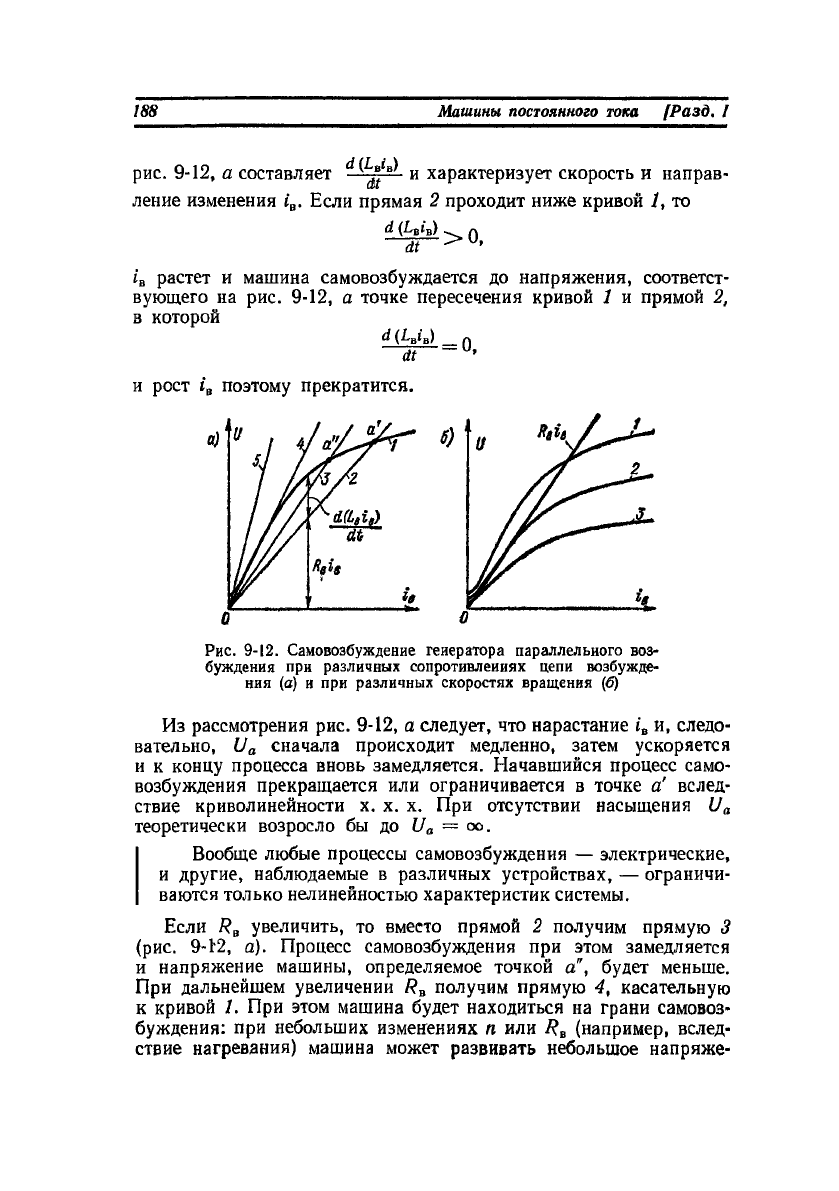
рис. 9-12, а составляет

d (L

)

и характеризует скорость и направ-

ление изменения i

. Если прямая 2 проходит ниже кривой 1, то

)

>0,

растет и машина самовозбуждается до напряжения, соответст-

вующего на рис. 9-12, а точке пересечения кривой 1 и прямой 2,

в которой

d(L

)

и рост i

поэтому прекратится.

Рис. 9-12. Самовозбуждение генератора параллельного воз-

буждения при различных сопротивлениях цепи возбужде-

ния (а) и при различных скоростях вращения (б)

Из рассмотрения рис. 9-12, а следует, что нарастание

i„

и, следо-

вательно, U

сначала происходит медленно, затем ускоряется

и к концу процесса вновь замедляется. Начавшийся процесс само-

возбуждения прекращается или ограничивается в точке а' вслед-

ствие криволинейности х. х. х. При отсутствии насыщения U

теоретически возросло бы до U

= оо.

Вообще любые процессы самовозбуждения — электрические,

и другие, наблюдаемые в различных устройствах, — ограничи-

ваются только нелинейностью характеристик системы.

Если R

увеличить, то вместо прямой 2 получим прямую 3

(рис. 9-12, а). Процесс самовозбуждения при этом замедляется

и напряжение машины, определяемое точкой а", будет меньше.

При дальнейшем увеличении R

получим прямую 4, касательную

к кривой 1. При этом машина будет находиться на грани самовоз-

буждения: при небольших изменениях п или R

(например, вслед-

ствие нагревания) машина может развивать небольшое напряже-

ние или терять его. Значение R

, соответствующее прямой 4, назы-

вается критическим (R

). При R

> R

B кр

(прямая 5)

самовозбуждение невозможно и напряжение машины определяется

остаточным потоком.

Из сказанного следует, что генератор параллельного возбуж-

дения может работать только при наличии определенного насыщения

магнитной цепи. Посредством изменения R

можно регулировать U

до значения U = U

KBiS

, соответствующего началу колена кривой

х. х. х. В машинах обычного исполнения U

= (0,65 0,75) U

Э. д. с. п, и для разных значений гц~> п

получим

х. х. х., изображенные на рис. 9-12, б кривыми 1, 2, 3. Из этого

рисунка видно, что при некотором значении R

в случае кривой 1

имеем устойчивое самовозбуждение, при кривой 2 машина находится

на грани самовозбуждения и при

кривой 3 самовозбуждение невоз-

можно. Поэтому для каждого

данного значения R„ существует

такое значение скорости вращения

ti = п

р (кривая 2 на рис. 9-12, б),

ниже которого самовозбуждение

невозможно. Такое значение п =

= п

р называется критиче-

ской скоростью вра-

щения.

В некоторых случаях требуется, чтобы U генератора парал-

лельного возбуждения можно было регулировать в широких пре-

делах, например U

HKB

— 5:1 или даже U:U

KaH

= 10:1 (возбу-

дители синхронных машин—см. раздел 5 и др.). Тогда кривая

х. х. х. должна искривляться уже в своей начальной части. С этой

целью в необходимых случаях в магнитной цепи выполняют участки

с ослабленным сечением (магнитные мостики насыщения) в виде

прорезей в листах сердечников полюсов (рис. 9-13, а), выступов

в верхней части этих листов (рис. 9-13, б) и т. п. В таких мостиках

происходит концентрация магнитного потока, и их насыщение

наступает уже при малых потоках.

Характеристика холостого хода U= f (i

) при / = 0 и ti = const

при параллельном возбуждении может быть снята только в одном

квадранте (рис. 9-14) путем регулирования i

с помощью регули-

ровочного реостата в цепи возбуждения (см. рис. 9-1, б). Так как

°к i

мал, то U да Е

, и характер кривой х. х. х. у генератора

параллельным возбуждением будет таким же, как и у генератора

независимым возбуждением.

Характеристика короткого замыкания / = f (г

) при U — 0 и

= const для генератора параллельного возбуждения может быть

снята только при питании обмотки возбуждения от постороннего

Рис. 9-13. Магнитные мостики на-

сыщения в магнитной цепи

источника, как и для генератора независимого возбуждения, так

как при самовозбуждении при U — 0 также i

= 0.

Внешняя характеристика U = f (/) генератора параллельного

возбуждения снимается при R

= const и п = const, т. е. без регу-

лирования в цепи возбуждения, при естественных условиях работы.

Вследствие этого к двум причинам падения напряжения, указанным

для генератора независимого возбуждения (см. § 9-3), прибавляется

третья — уменьшение i

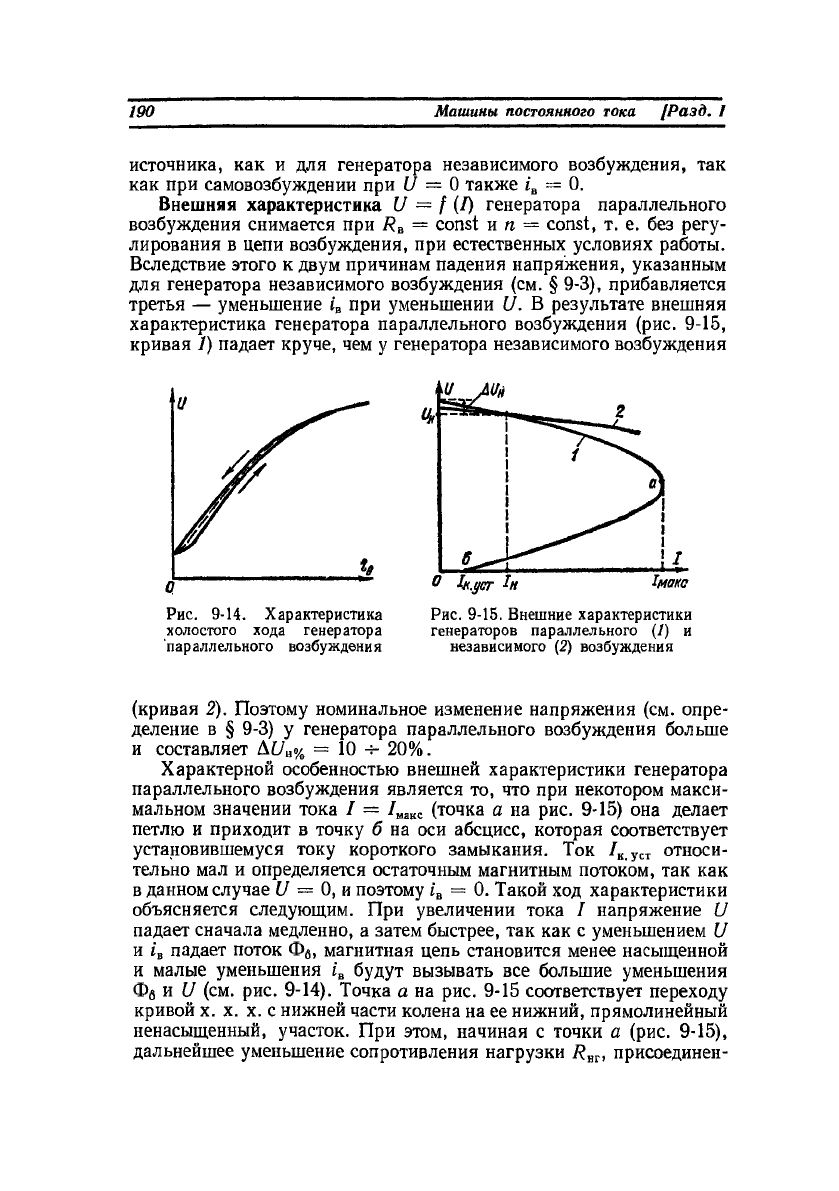
при уменьшении U. В результате внешняя

характеристика генератора параллельного возбуждения (рис. 9-15,

кривая 1) падает круче, чем у генератора независимого возбуждения

Рис. 9-14. Характеристика

холостого хода генератора

параллельного возбуждения

(кривая 2). Поэтому номинальное изменение напряжения (см. опре-

деление в § 9-3) у генератора параллельного возбуждения больше

и составляет Af/

% = Ю ч- 20%.

Характерной особенностью внешней характеристики генератора

параллельного возбуждения является то, что при некотором макси-

мальном значении тока I — /

макс

(точка а на рис. 9-15) она делает

петлю и приходит в точку б на оси абсцисс, которая соответствует

установившемуся току короткого замыкания. Ток /

уст

относи-

тельно мал и определяется остаточным магнитным потоком, так как

в данном случае U = 0, и поэтому i

= 0. Такой ход характеристики

объясняется следующим. При увеличении тока / напряжение U

падает сначала медленно, а затем быстрее, так как с уменьшением U

и i

падает поток Фв, магнитная цепь становится менее насыщенной

и малые уменьшения i

будут вызывать все большие уменьшения

Фв и U (см. рис. 9-14). Точка а на рис. 9-15 соответствует переходу

кривой х. х. х. с нижней части колена на ее нижний, прямолинейный

ненасыщенный, участок. При этом, начиная с точки а (рис. 9-15),

дальнейшее уменьшение сопротивления нагрузки R

, присоединен-

Рис. 9-15. Внешние характеристики

генераторов параллельного (1) и

независимого (2) возбуждения