Винокуров В.Н. Лекции по теоретической механике

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей

61

Решение. Выразим декартовы координаты точек приложения сил через обобщённую коор-

динату. Сила

gm

1

приложена посередине стержня 1, в точке

1

C . Координаты этой точки

ϕ

cos

2

1

l

x

C

= ,

ϕ

sin

2

1

l

y

C

= . Координаты точки

2

C приложения силы gm

2

:

ϕ

cos

2

3

2

l

x

C

= ,

ϕ

sin

2

l

y

C

=

. Координаты точки

B

приложения сил gm

3

и F :

ϕ

cos2lx

B

=

, 0=

B

y .

Запишем значения проекций действующих сил: 0)()()(

321

=

==

yxxx

Fgmgmgm ,

ggm

y

4)(

1

−= , ggm

y

3)(

2

−

= , ggm

y

−

=

)(

3

, 20

−

=

x

F .

По формуле (16.12)

ϕϕ

ϕ

sin8cos7,0

1

+−=

⎟

⎠

⎞

⎜

⎝

⎛

∂

+

∂

=

∑

=

g

y

F

x

FQ

N

k

ky

k

kx

.

2. Если задать системе такое возможное перемещение, при котором лишь одна из

обобщённых координат

i

q получает приращение

i

q

δ

, то из (16.13) следует

i

q

N

k

i

q

FA

Q

i

δ

⎥

⎦

⎤

⎢

⎣

⎡

=

∑

=1

)(

)...,,2,1( ni

=

. (16.14)

Индекс

i

q в числителе (16.14) как раз означает, что работа сил определяется на та-

ком перемещении системы, при котором изменяется лишь

я

−

i обобщённая коорди-

ната получает бесконечно малое изменение

i

q

δ

, а остальные обобщённые координа-

ты не меняются. Данный способ наиболее употребителен, поскольу всегда эффекти-

вен.

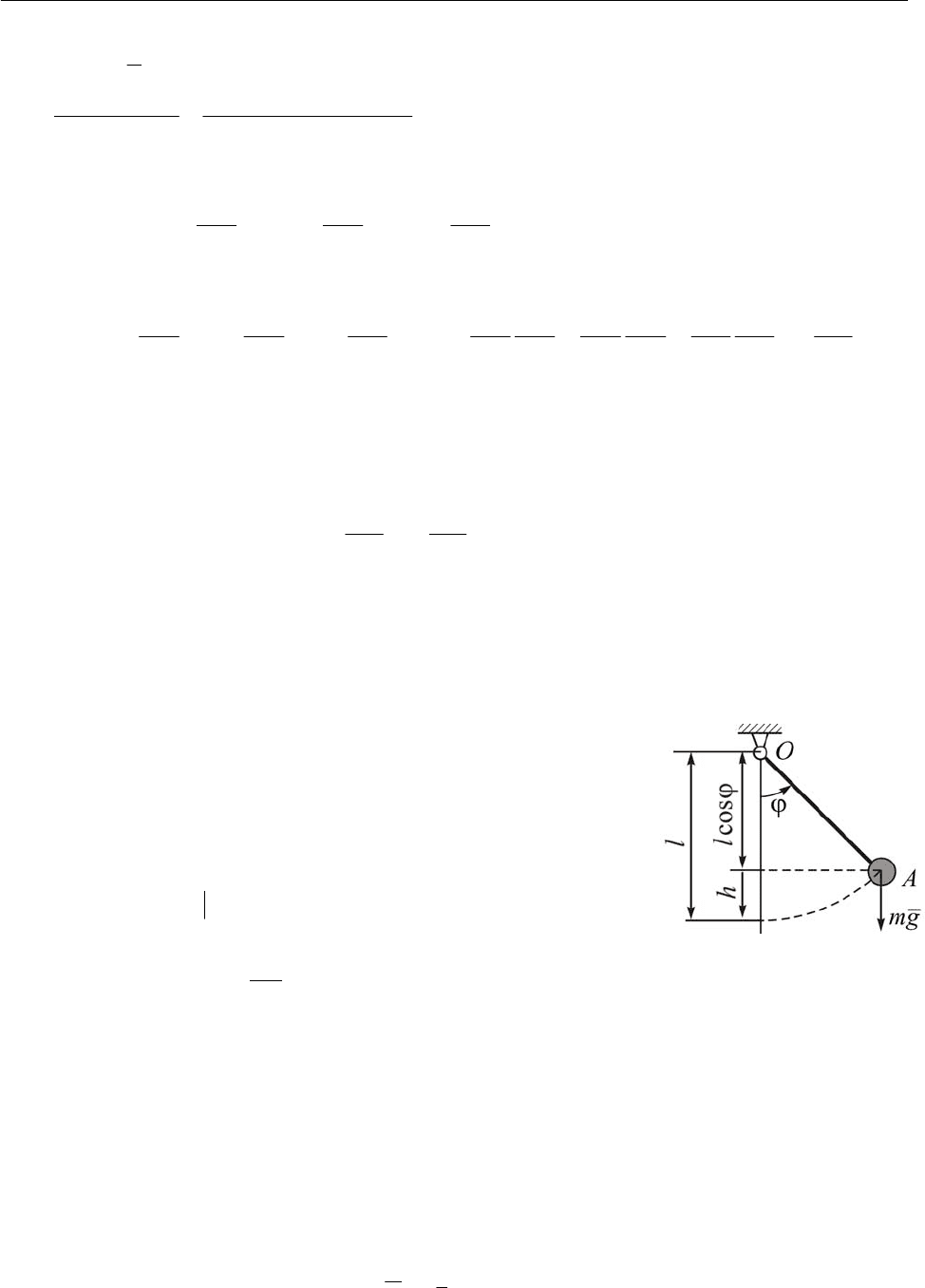
Пример. Ползун 1 массы

1

m может без трения пере-

мещаться по плоскости, наклонённой под углом

α

к го-

ризонту. С ползуном шарниром связан невесомый стер-

жень

ОА длины l , на конце которого закреплена мате-

риальная точка массы

2

m (рис. 16.9).

Полагая, что механизм совершает движение в верти-

кальной плоскости, выбрать обобщённые координаты и

вычислить соответствующие им обобщённые силы.

Решение. Система имеет две степени свободы. Ко-

ординатой

s определим положение ползуна. Координа-

той

ϕ

определим отклонение стержня

ОА

относительно

вертикали.

Для вычисления обобщённой силы

s

Q полагаем, что

система совершила из произвольного положения такое

перемещение, при котором координата

s возросла на

сколь угодно малую величину s

δ

, а координата

ϕ

не изменилась, 0

=

δϕ

. Тогда,

α

δ

αδαδ

δ

sin)(

)90cos()90cos(

)(

21

1

gmm

s

sgmsgm

s

FA

Q

s

N

k

s

+=

−°⋅⋅+−°⋅⋅

=

⎥

⎦

⎤

⎢

⎣

⎡

=

∑

=

.

Для вычисления

ϕ

Q представим, что система совершила из произвольного положения такое

перемещение, при котором координата

s не изменилась, 0

=

s

δ

, а координата

ϕ

изменилась на

сколь угодно малую величину

δϕ

. Тогда

Рис. 16.9

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей

62

ϕ

δϕ

ϕδϕ

δϕ

δ

ϕ

sin

)90cos(

)(

2

1

glm

lgm

FA

Q

N

k

−=

+°⋅⋅

=

⎥

⎦

⎤

⎢

⎣

⎡

=

∑

=

.

3. Если все силы потенциальны, то их проекции, согласно (14.55), вычисляются

по формулам

k

kx

x

U

F

∂

= ,

k

ky

y

U

F

∂

= ,

k

kz

z

U

F

∂

= . Подставив эти значения проекций в

формулу (16.12) определения обобщённой силы, получим

i

N

k

i

k

ki

k

ki

k

N

k

i

k

kz

i

k

ky

i

k

kxi

q

U

q

z

U

q

y

U

q

x

U

q

z

F

q

y

F

q

x

FQ

∂

=

⎟

⎠

⎞

⎜

⎝

⎛

∂

+

∂

+

∂

=

⎟

⎠

⎞

⎜

⎝

⎛

∂

+

∂

+

∂

=

∑∑

== 11

.

Таким образом, если все силы потенциальны и известна силовая функция

U

(или

потенциальная энергия

П

), то обобщённые силы могут быть вычислены как част-

ные производные от силовой функции по соответствующим обобщённым координа-

там:

ii

i

q

П

q

U

Q

∂

−=

∂

= )...,,2,1( ni

=

.

Пример. На рисунке 16.10 изображён математический маятник, т.е. невесомый стержень

OA

длины

l , закреплённый концом O с помощью неподвижного цилиндрического шарнира, на дру-

гом конце которого прикреплена материальная точка массы

m .

Найти обобщённую силу, применив третий способ её вычисления.

Решение. Система имеет одну степень свободы. За обоб-

щённую координату примем угол

ϕ

отклонения маятника от

вертикали. При движении маятника работу будет совершать

лишь сила тяжести, которая относится к потенциальным. Вы-

числим потенциальную энергию как работу сил при перемеще-

нии системы из произвольного положения в положение равно-

весия:

)cos(

0

ϕ

llmgmghАП

M

−=== .

Тогда,

ϕ

sinmgl

П

Q −=

∂

−= .

16.7. Принцип возможных перемещений. Данный принцип устанавливает усло-

вие равновесия

механических систем, подчинённых идеальным, стационарным свя-

зям.

Чтобы данное положение механической системы с идеальными стационарными

связями было положением равновесия, необходимо и достаточно, чтобы сумма

элементарных работ всех активных сил на любом возможном перемещении систе-

мы из этого положения была равна нулю:

0

1

=⋅

∑

=

N

k

kk

rF

δ

. (16.15)

Рис. 16.10

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей

63

Доказательство необходимости. Пусть механическая система, состоящая из

N

материальных точек, находится в равновесии. Тогда приложенные к произвольной

точке активные силы и реакции связей составляют уравновешенную систему сил,

0

=

+

kk

RF

N

k

...,,2,1

=

. (16.16)

Умножив скалярно каждое из уравнений (16.16) на вектор

k

r

δ

возможного пере-

мещения ой−

k

точки и просуммировав по всем уравнениям, получим

0

11

=⋅+⋅

∑∑

==

N

k

kk

N

k

kk

rRrF

δδ

.

С учётом определения идеальных связей последнее уравнение эквивалентно уравне-

нию (16.15). Тем самым доказана необходимость.

Доказательство достаточности проведём методом от противного. Пусть для неко-

торого положения системы выполняется равенство (16.15). Но, помещённая в это

положение система с нулевыми скоростями точек, пришла в движение. Значит, най-

дётся точка системы, которая за промежуток времени

d

t

совершит действительное

перемещение

k

rd , которое будет направлено по равнодействующей

kk

RF

+

и, сле-

довательно,

0)( >⋅+

kkk

rdRF . Для стационарных связей действительное перемеще-

ние

k

rd

совпадает с одним из возможных

k

r

δ

. Учитывая это и суммируя последние

неравенства по всем точкам системы, получим

0)(

1

>⋅+

∑

=

N

k

kkk

rRF

δ

⇒ 0

11

>⋅+⋅

∑∑

==

N

k

kk

N

k

kk

rRrF

δδ

⇒ 0

1

>⋅

∑

=

N

k

kk

rF

δ

.

Полученный результат противоречит равенству (16.15). Это указывает на то, что

предположение о нарушении равновесия системы ошибочно и, тем самым, доста-

точность принципа доказана.

Примечание. Для изучающих принцип возможных перемещений впервые, кажется парадок-

сальным, что одно уравнение (16.15) описывает всё состояние равновесия механической системы,

помня из статики, что равновесие пространственной системы сил описывается шестью скалярны-

ми уравнениями. «Разгадка парадокса» в том, что уравнений (16.15) можно получить столько,

сколько необходимо, вычисляя сумму работ на различных возможных перемещениях системы.

16.8. Условие равновесия механической системы в обобщённых силах. Если

положение механической системы из

N

материальных точек, в силу наложенных на

неё голономных стационарных удерживающих связей, определено обобщёнными

координатами

n

qqq ,...,,

21

, то радиус-вектор каждой точки будет функцией этих ко-

ординат:

),...,,(

21 nkk

qqqrr =

. Вариация радиус-вектора через вариации обобщённых

координат определяется по формуле

∑

=

∂

=

n

i

k

q

r

1

δδ

(см. 16.11). Тогда уравнение

принципа возможных перемещений (16.15) можно преобразовать к виду

0

11111

==

⎟

⎠

⎞

⎜

⎝

⎛

∂

⋅=

⎟

⎠

⎞

⎜

⎝

⎛

∂

⋅

∑∑∑∑∑

=====

n

i

ii

n

i

N

k

i

k

N

k

n

i

k

qQq

q

r

Fq

q

r

F

δδδ

.

Так как вариации обобщённых координат взаимно независимы, то последнее урав-

нение будет выполняться лишь в случае, если все обобщённые силы раны нулю:

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей

64

0

=

i

Q , ni ...,,2,1

=

. (16.17)

Полученная система из n уравнений есть условия равновесия механической систе-

мы в обобщённых силах: для того, чтобы некоторое положение механической сис-

темы, подчинённой идеальным голономным стационарным связям было положени-

ем равновесия, необходимо и достаточно равенства нулю в этом положении всех

обобщённых сил.

Пример. Для математического маятника, показанного на рисунке 16.10, была вычислена обоб-

щённая сила

ϕ

sinmglQ −= . Согласно (16.17), положения равновесия маятника определяются из

уравнения

0sin =−

ϕ

mgl

, которое даёт два очевидных решения: 0

1

=

ϕ

,

π

ϕ

=

2

.

Если все силы потенциальны, то обобщённые силы, как было доказано выше,

можно выразить через силовую функцию (либо потенциальную энергию) по форму-

ле

ii

i

q

П

q

U

Q

∂

−=

∂

= . В этом случае условие равновесия (16.17) преобразуются к виду

0=

∂

i

q

U

либо

0=

∂

i

q

П

, ni ...,,2,1

=

.

16.9. Принцип Даламбера-Лагранжа. Общее уравнение динамики. Рассмот-

рим систему, состоящую из

N

материальных точек. В соответствие с принципом

Даламбера, приложенные к каждой точке активные силы, реакции связей и силы

инерции в любой момент времени образуют уравновешенную систему сходящихся

сил:

0

=

Φ

+

kkk

RF . (16.18)

Здесь

k

F

и

k

R

- равнодействующие активных сил и реакций связей, приложенных к

ой−

k

точке,

kkk

am−=Φ – сила инерции.

Умножим обе части уравнения (16.18) скалярно на возможное перемещение

k

r

δ

ой−

k

точки и просуммируем полученные для всех точек системы произведения. В

результате имеем

()

∑

=

=⋅Φ++

N

k

kkkk

rRF

1

0

δ

. (16.19)

Это уравнение выражает принцип Даламбера-Лагранжа: при движении механиче-

ской системы в любой момент времени сумма работ активных сил, сил реакций

связей и сил инерции на любом возможном перемещении из занимаемого положения

равна нулю. Ещё это уравнение называют общим уравнением динамики, потому что

из него могут быть выведены все

другие уравнения, описывающие движения меха-

ническим систем.

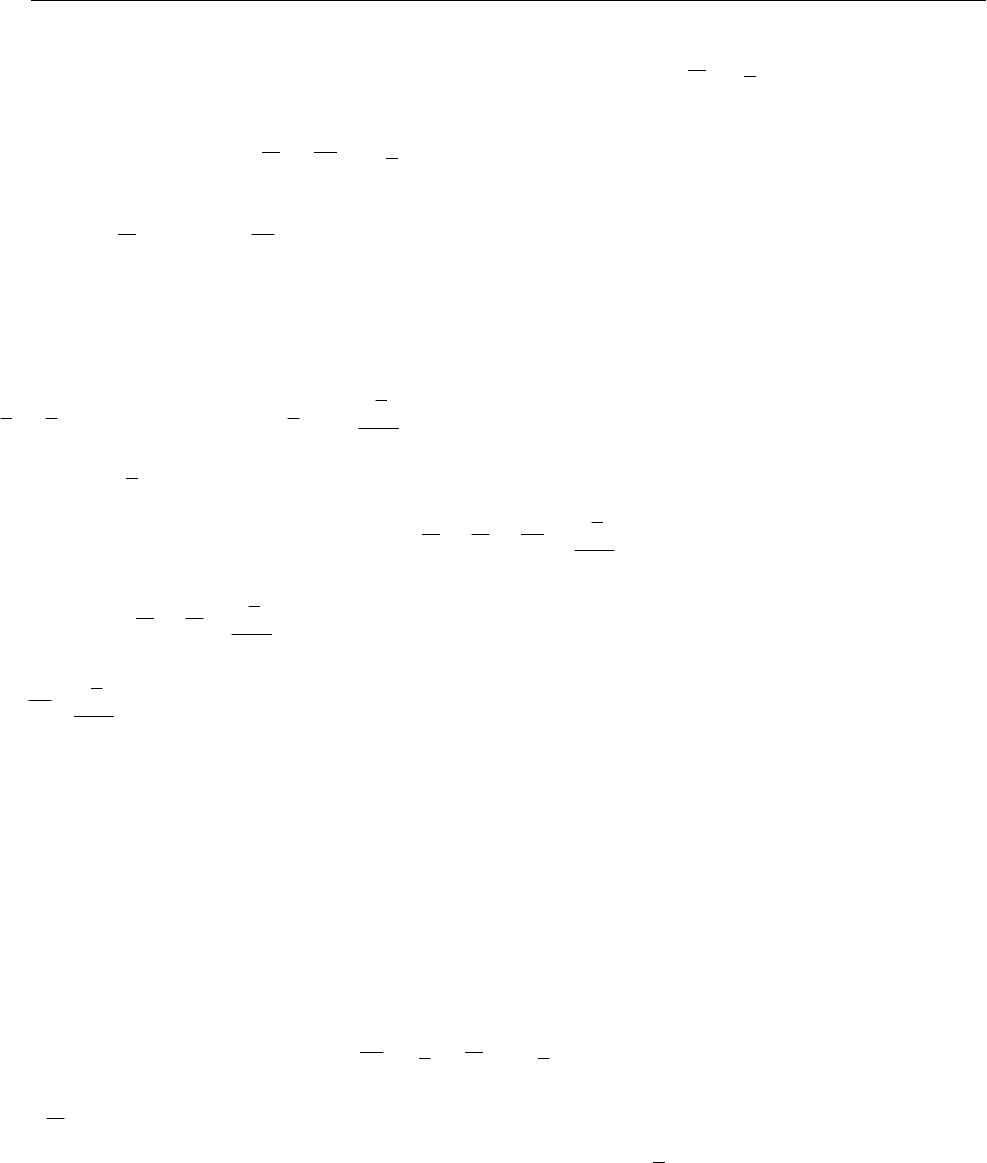
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей

65

Если связи, наложенные на систему, идеальные, то

∑

=

=⋅

N

k

kk

rR

1

0

δ

и общее урав-

нение примет вид

()

∑

=

=⋅Φ+

N

k

kkk

rF

1

0

δ

, что можно записать и в несколько иной фор-

ме:

0)()(

11

=+

∑∑

==

N

k

N

k

ФAFA

δδ

.

При движении системы с идеальными связями в любой момент времени должна

быть равна нулю сумма возможных работ активных сил и сил инерции.

Если для изучения движения системы применяют обобщённые координаты, то

()

tqqqrr

nkk

,,...,,

21

= и

∑

=

∂

=

n

i

k

q

r

1

δδ

. Подставив выражение для возможного пере-

мещения

k

r

δ

в (16.19) и изменив порядок суммирования, получим

()

∑∑

==

=

⎥

⎦

⎤

⎢

⎣

⎡

∂

⋅Φ++

n

i

k

N

k

kkk

q

r

RF

11

0

δ

. (16.20)

Так как

()

∑

=

∂

⋅+

N

k

i

k

kk

Q

q

r

RF

1

- обобщённая сила, соответствующая i -й координате, то

∑

=

∂

⋅Φ

N

k

ИН

i

k

Q

q

r

1

- обобщённая сила инерции, соответствующая той же координате.

Вследствие независимости между собой вариаций обобщённых координат, условие

(16.20) принимает вид

0=+

ИН

ii

QQ , ni ...,,2,1

=

.

Последнее выражение называется общим уравнением динамики в обобщённых си-

лах.

При изучении движения твёрдого тела силы инерции нужно привести к какому-

либо центру, например центру масс тела. Тогда сумму возможных работ сил инер-

ции можно вычислить следующим образом:

∑

=

⋅+⋅=⋅Φ

N

k

ИН

CИНkk

LrRr

1

δϕδδ

ω

,

где

ИН

R ,

ИН

L

ω

- главный вектор и главный момент сил инерции относительно мгно-

венной оси вращения, проходящей через центр масс;

C

r

δ

- возможное перемещение

центра масс;

δϕ

- возможный угол поворота тела вокруг мгновенной оси вращения.

16.10. Уравнения Лагранжа второго рода. Уравнения Лагранжа второго рода

представляют собой дифференциальные уравнения движения несвободной механи-

ческой системы, составленные в обобщённых координатах.

Пусть на движение механической системы из

N

материальных точек наложены

m идеальных голономных удерживающих связей. Общее уравнение динамики для

такой системы имеет вид

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей

66

()

∑

=

=⋅−

N

k

kkkk

rrmF

1

0

δ

&&

. (16.21)

Определим положение системы обобщёнными координатами

n

qqq ,...,,

21

, где

m

N

n −= 3. Тогда радиус-вектор каждой точки будет функцией указанных коорди-

нат и времени,

()

tqqqrr

nkk

,,...,,

21

=

, а возможное перемещение ой−

k

точки вычис-

ляется по формуле

∑

=

∂

=

n

i

k

q

r

1

δδ

. (16.22)

Подставив (16.22) в (16.21) и поменяв порядок суммирования, получим

0

11 1

=

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

∂

⋅−

∂

⋅

∑∑ ∑

== =

n

i

N

k

N

k

i

kk

k

i

k

q

r

dt

rd

m

q

r

F

δ

&

. (16.23)

Первое слагаемое в квадратных скобках есть обобщённая сила соответствующая

ой−i обобщённой координате:

i

N

k

i

k

Q

q

r

F =

∂

⋅

∑

=1

. Преобразуем выражение

⎟

⎠

⎞

⎜

⎝

⎛

∂

⋅

i

kk

q

r

dt

rd

&

:

⎟

⎠

⎞

⎜

⎝

⎛

∂

⋅−

⎟

⎠

⎞

⎜

⎝

⎛

∂

⋅=

⎟

⎠

⎞

⎜

⎝

⎛

∂

⋅

i

k

ii

kk

q

r

dt

d

r

q

r

dt

d

q

r

dt

rd

&&

&

. (16.24)

Выведем теперь два вспомоготельных тождества. Так как

∑

=

∂

+

∂

=

n

i

k

i

k

t

r

q

r

1

&

, то

i

k

i

k

q

r

q

r

∂

=

∂

&

. (16.25)

Равентво (16.25) называется

первым тождеством Лагранжа. Заменив на осно-

вании этого тождества производную

i

k

q

r

∂

на

i

k

q

r

&

∂

в первом слагаемом выражения

(16.24), получим

.

2

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

⎟

⎠

⎞

⎜

⎝

⎛

∂

⋅=

⎟

⎠

⎞

⎜

⎝

⎛

∂

⋅

k

ik

k

i

k

r

qdt

d

q

r

dt

d

q

r

dt

d

&

&&

&

&&

Следовательно,

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

⎟

⎠

⎞

⎜

⎝

⎛

∂

∑∑

==

i

N

k

N

k

kk

ii

k

kk

q

T

dt

drm

qdt

d

q

r

dt

d

m

&

11

2

, (16.26)

где

T

- кинетическая энергия механической системы.

Преобразуем теперь производную

⎟

⎠

⎞

⎜

⎝

⎛

∂

i

k

q

r

dt

d

. Так как

()

tqqqrr

nkk

,,...,,,

21

= , то

⎟

⎠

⎞

⎜

⎝

⎛

∂

i

k

q

r

- функция обобщённых координат и времени. Поэтому, с одной стороны,

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей

67

i

k

n

in

k

i

k

i

k

i

k

qt

r

q

qq

r

q

qq

r

q

qq

r

q

r

dt

d

∂∂

∂

+

∂∂

∂

++

∂∂

∂

+

∂∂

∂

=

⎟

⎠

⎞

⎜

⎝

⎛

∂

22

2

1

2

...

&&&

. (16.27)

С другой стороны,

∑

=

∂

+

∂

=

n

i

k

i

k

t

r

q

r

1

&

и

tq

r

q

qq

r

q

qq

r

q

qq

r

q

r

i

k

n

ni

k

i

k

i

k

i

k

∂∂

∂

+

∂∂

∂

+

∂∂

∂

+

∂∂

∂

=

∂

22

2

1

2

...

&&&

&

. (16.28)

Сопоставляя (16.27) и (16.28), заключаем, что

i

k

i

k

q

r

q

r

dt

d

∂

=

⎟

⎠

⎞

⎜

⎝

⎛

∂

&

.

Это

второе тождество Лагранжа. С учётом данного тождества, получаем

i

N

k

kk

i

N

k

i

k

kk

N

k

i

k

kk

q

T

rm

qq

r

rm

q

r

dt

d

rm

∂

=

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

∂

⋅=

⎟

⎠

⎞

⎜

⎝

⎛

∂

∑∑∑

=== 1

2

11

2

&&

. (16.29)

С учётом (16.24), (16.26), (16.29) и определения обобщённой силы общее уравне-

ние динамики (16.23) можно записать в виде

0

1

=

⎥

⎦

⎤

⎢

⎣

⎡

∂

+

⎟

⎠

⎞

⎜

⎝

⎛

∂

−

∑

=

i

n

i

ii

i

q

T

q

T

dt

d

Q

δ

&

. (16.30)

Вследствии независимости между собой вариаций

i

q

δ

обобщённых координат,

уравнение (16.30) будет выполняться лишь в случае, если равны нулю выражения в

квадратных скобках, т.е. если

i

ii

Q

q

T

q

T

dt

d

=

∂

−

⎟

⎠

⎞

⎜

⎝

⎛

∂

&

, ni ...,,2,1

=

. (16.31)

Уравнения (16.31) называются уравнениями Лагранжа второго рода. Число этих

уравнений равно числу степеней свободы.

16.11. Уравнения Лагранжа в случае потенциальных сил. Циклические ко-

ординаты и циклические интегралы

. Если все силы, действующие на точки сис-

темы потенциальны, то обобщённые силы вычисляются через потенциальную энер-

гию

),...,,,(

21

tqqqПП

n

= по формуле

i

q

П

Q

∂

−= . Тогда уравнения Лагранжа (16.31)

могут быть записаны в виде

iii

q

П

q

T

q

T

dt

d

∂

−=

∂

−

⎟

⎠

⎞

⎜

⎝

⎛

∂

&

.

Функция, равная разности кинетической и потенциальной энергий механической

системы, называется функцией Лагранжа:

П

T

L

−

=

.

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей

68

Так как потенциальная энергия не зависит от обобщённых скоростей, 0≡

∂

i

q

П

&

, то

ii

q

T

q

L

&&

∂

=

∂

. При использовании функции Лагранжа уравнения (16.31) имеют вид

0=

∂

−

⎟

⎠

⎞

⎜

⎝

⎛

∂

ii

q

L

q

L

dt

d

&

.

Обобщённая координата, которая явно не входит в выражение функции Лагран-

жа, называется циклической координатой. Если

j

q – циклическая координата, то

0=

∂

j

q

L

и из последнего уравнения следует 0=

⎟

⎠

⎞

⎜

⎝

⎛

∂

j

q

L

dt

d

&

, откуда, в свою очередь,

получаем, что функция

j

q

L

&

∂

не меняется:

constC

q

L

j

==

∂

&

.

Функция координат, скоростей и времени, которая не меняется на решениях диф-

ференциальных уравнений, называется первым интегралом. Значение первых инте-

гралов в том, что они упрощают интегрирование дифференциальных уравнений. Та-

ким образом, если удаётся выбрать циклические координаты, то это гарантирует

существование первых интегралов, называемых в этом случае циклическими инте-

гралами.

16.12. Структура уравнений Лагранжа второго рода. Кинетическая энергия

механической системы, состящей из

N

материальных точек, определяется по фор-

муле

∑

=

N

k

kk

rmT

1

2

1

&

. Если данная система с голономными нестационарными связями

имеет

n степеней свободы, то

∑

=

∂

+

∂

=

n

i

k

i

k

t

r

q

r

1

&

и кинетическую энергию системы

можно записать так:

∑∑∑∑∑

=====

++=

⎟

⎠

⎞

⎜

⎝

⎛

∂

+

∂

=

n

i

ii

n

i

n

j

jiij

N

k

n

i

k

i

k

CqBqqA

t

r

q

r

mT

1111

2

1

2

1

2

1

2

1

&&&&

, (16.32)

где введены обозначения

j

k

N

k

i

k

kij

q

r

q

r

mA

∂

=

∑

=1

,

∑

=

∂

=

N

k

i

k

ki

t

r

q

r

mB

1

,

∑

=

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

N

k

t

r

mC

1

.

Если наложенные на систему связи стационарные, то

0=

∂

t

r

k

и тогда 0

=

i

B ,

0

=

C

. В этом случае кинетическая энергия системы является однородной квадра-

тичной формой обобщённых скоростей:

∑∑

==

=

n

i

n

j

jiij

qqAT

11

2

1

&&

. (16.33)

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей

69

Производные от кинетической энергии (16.33), соответствующие левой части

уравнений Лагранжа, равны

∑

=

∂

n

j

jij

i

qA

q

T

1

&

,

∑∑∑∑∑

==−=−

⎟

⎠

⎞

⎜

⎝

⎛

∂

+=+=

⎟

⎠

⎞

⎜

⎝

⎛

∂

n

j

n

i

ij

n

j

jij

n

j

ij

n

j

jij

i

qq

q

A

qAq

dt

dA

qA

q

T

dt

d

11111

&&&&&&&

&

,

∑∑

==

∂

=

∂

n

i

n

j

ji

i

ij

i

qq

q

A

q

T

11

2

1

&&

.

Подставляя эти выражения в уравнения Лагранжа, получаем

i

n

j

n

j

n

i

n

i

n

j

ji

i

ij

i

ij

jij

Qqq

q

A

qq

q

A

qA =

∂

−

∂

+

∑∑∑ ∑∑

=== ==111 11

2

1

&&&&&&

, ni ...,,2,1

=

. (16.34)

Обобщённые силы

i

Q есть функции обобщённых координат, времени и, возмож-

но, обобщённых скоростей. Тогда из (16.34) следует, что наивысший порядок про-

изводных по времени от обобщённых координат – второй. Порядок уравнений не

изменится и при нестационарных связях.

Таким образом, уравнения Лагранжа второго рода для механической системы с

голономными связями представляют собой систему обыкновенных дифференциаль-

ных

уравнений порядка n2 относительно обобщённых координат.

Последовательность действий при использовании уравнений Лагранжа второго

рода при решеии задач следующая:

1) определить число степеней свободы системы и выбрать наиболее удобные

обобщённые координаты;

2) вычислить кинетическую энергию системы в её абсолютном движении и выра-

зить эту энергию через обобщённые скорости и, возможно, обобщённые кординаты;

3) вычислить производные от

кинетической энергии, входящие в левую часть

уравнений Лагранжа;

4) определить обобщённые силы, соответствующие обобщённым координатам;

5) подставить все вычисленные величины в уравнения Лагранжа.

Пример. Планетарный механизм, состоящий водила 1 массы

1

m , сателлита 2 массы

2

m и не-

подвижной солнечной шестерни 3 движется в горизонтальной плоскости под действием постоян-

ного вращающего момента

вр

M приложенного к водилу (рис.

16.11).

Приняв звено 1 за однородный стержень, а звено 2 за одно-

родный диск, составить дифференциальное уравнение движения

данной механической системы.

Радиусы второго и третьего звеньев одинаковы и равны

r

.

Проскальзывание между звеньями 2 и 3 отсутствует.

Решение. Система имеет одну степень свободы. За обоб-

щённую координату примем угол поворота

ϕ

звена 1. Следова-

тельно, движение механизма будет описываться уравнением Ла-

гранжа

Q

TT

dt

d

=

∂

−

⎟

⎠

⎞

⎜

⎝

⎛

∂

ϕϕ

&

.

Считаем, что кривошип вращается с угловой скоростью

ϕ

&

в положительном направлении от-

счёта угла

ϕ

. Кинетическая энергия системы

21

TTT

+

=

. Первое звено совершает вращательное

Рис. 16.11

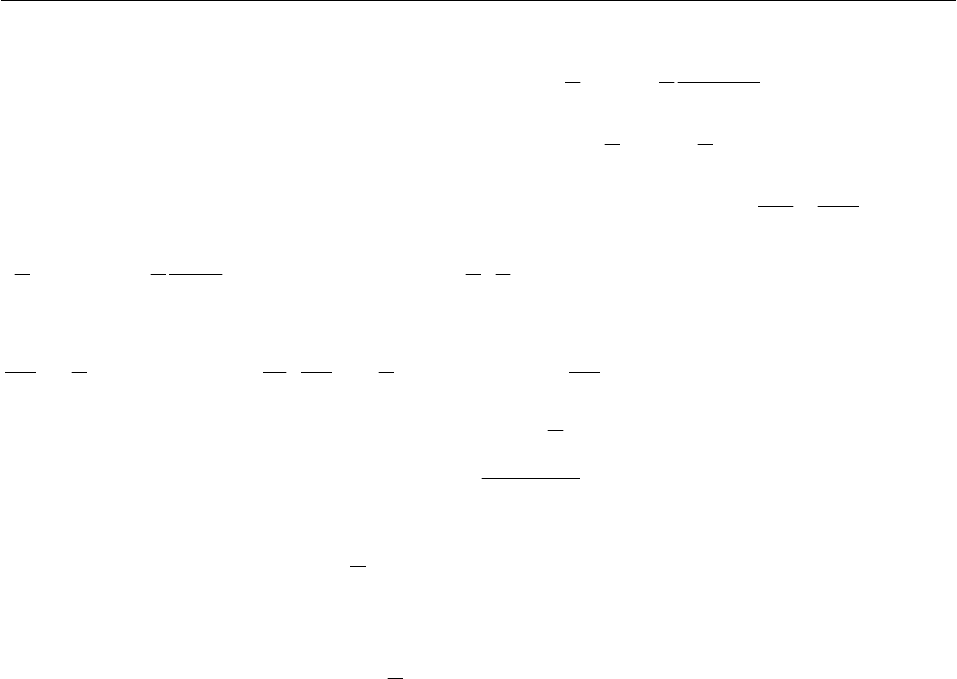
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей

70

движение вокруг неподвижной оси. Следовательно

2

1

2

111

3

)2(

2

1

2

1

ϕω

&

rm

JT ==

. Второе звено со-

вершает плоское движение. Его кинетическая энергия

2

22

2

22

2

1

2

1

ωυ

JmT

A

+= . Скорость точки

A

ϕ

ω

υ

&

rOA

A

2

1

== . Угловая скорость звена 2 при плоском его движении

ϕ

υ

ω

&

2

===

r

AP

A

. Тогда

22

2

22

3)2(

22

1

)2(

2

1

ϕϕϕ

&&&

rm

rmT =+= ,

22

21

6

3

4

2

1

ϕ

&

rmmT

⎟

⎠

⎞

⎜

⎝

⎛

+= .

Вычислим производные от кинетической энергии.

ϕ

&

2

21

6

3

4

rmm

T

⎟

⎠

⎞

⎜

⎝

⎛

+=

∂

,

ϕ

&&

&

2

21

6

3

4

rmm

T

dt

d

⎟

⎠

⎞

⎜

⎝

⎛

+=

⎟

⎠

⎞

⎜

⎝

⎛

∂

, 0=

∂

ϕ

T

.

Обобщённую силу вычислим по формуле

δϕ

δ

∑

=

N

k

FA

Q

1

)(

, для чего представим, что угол

ϕ

уве-

личился на сколь угодно малую величину

δϕ

. На таком перемещении системы лишь момент сил

вр

М совершит работу. Тогда

δϕδ

вр

N

k

МFA =

∑

=1

)(,

вр

МQ

=

. Подставляя найденные величины в

уравнение Лагранжа, получим

вр

Мrmm =

⎟

⎠

⎞

⎜

⎝

⎛

+

ϕ

&&

2

21

6

3

4

.

Последнее уравнение является ответом в задаче.

ЛИТЕРАТУРА

1.

Дронг В.И. и др. Курс теоретической механики. Под ред. Колесникова. - М.:

МГТУ, 2002. - 736 с.

2.

Тарг С.М. Краткий курс теоретической механики. – М.: Высшая школа, 2002. –

416 с.

Винокуров В.Н. Лекции по теоретической механике

Подождите немного. Документ загружается.