Винокуров В.Н. Лекции по теоретической механике
Подождите немного. Документ загружается.


В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
41
()
∑∑ ∑∑∑
== ===
++===
N
k
N
k
N
k
r
kk
r
k
C
kCk
N
k
kk
N
k
kk
mmmmmT
11
2
1
2
1
2
1
2
2
1
2
1
2
1
2
1
υυυυυυ
.
Здесь
0
1111
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
===⋅
∑∑∑∑
====
N
k
kkC
N
k
k
kC
N
k
N
k
r
kkC
r
kCk
m
dt
d
dt
d
mmm
ρυ
ρ
υυυυυ
,
поскольку
∑
=
==
N
k
Ckk
Mm
1
0
ρρ
.
Таким образом,
r
CC
TMT +=
2
2
1
υ
, (14.44)
где
∑
=
=
N
k
k
mM
1
– масса механической системы,
(
)
∑
=
=
N
k
r
kk
r
C
mT
1
2
2
1
υ
– кинетическая
энергия системы в её движении относительно кёниговой системы отсчёта.
Формула (14.44) выражает теорему Кенига: кинетическая энергия механической
системы в её абсолютном движении равна сумме кинетической энергии центра
масс, в предположении, что в нём сосредоточена вся масса системы, и кинетиче-
ской энергии системы относительно центра масс.
14.19. Кинетическая энергия твёрдого тела при поступательном, вращатель-
ном и плоском его движениях
. При поступательном движении твёрдого тела ско-
рости всех его точек одинаковы и равны скорости центра масс, поэтому
2
1
2
1
2
1
2
2
1
222
C
N
k
k
C
N
k
Ck
N
k
kk
пост
Mm
mm
T
υ
υυυ
====
∑∑∑
===
,
где
M
- масса твёрдого тела.
При вращении твёрдого тела вокруг неподвижной оси Oz с угловой скоростью
ω
скорость его произвольной точки
kk
h
ω
υ
=
,
где
k
h - кратчайшее расстояние от точки
k
M до оси вращения.
Тогда
()
2
1
2
2
1
2
1
2
2
1
22
1
2
1
ω
ω
ωυ
z
N
k
kk
N
k
kk
N
k
kkвр
JhmhmmT ====
∑∑∑
===
,
где
∑
=
=
N
k
kkz
hmJ
1
2
– момент инерции тела относительно оси вращения Oz .
Плоское движение твёрдого тела можно рассматривать как совокупность посту-
пательного движения вместе с центром масс со скоростью
C
υ
и вращательного
движения с угловой скоростью
ω
вокруг подвижной оси zC
′
, движущейся поступа-
тельно вместе с центром масс. Тогда кинетическая энергия относительного движе-
ния
2
2
1
ω
zCвр
r
C
JTT
′
== и по теореме Кёнига
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
42
22
2
1
2
1
ωυ
zCCпл
JMT
′
+= .
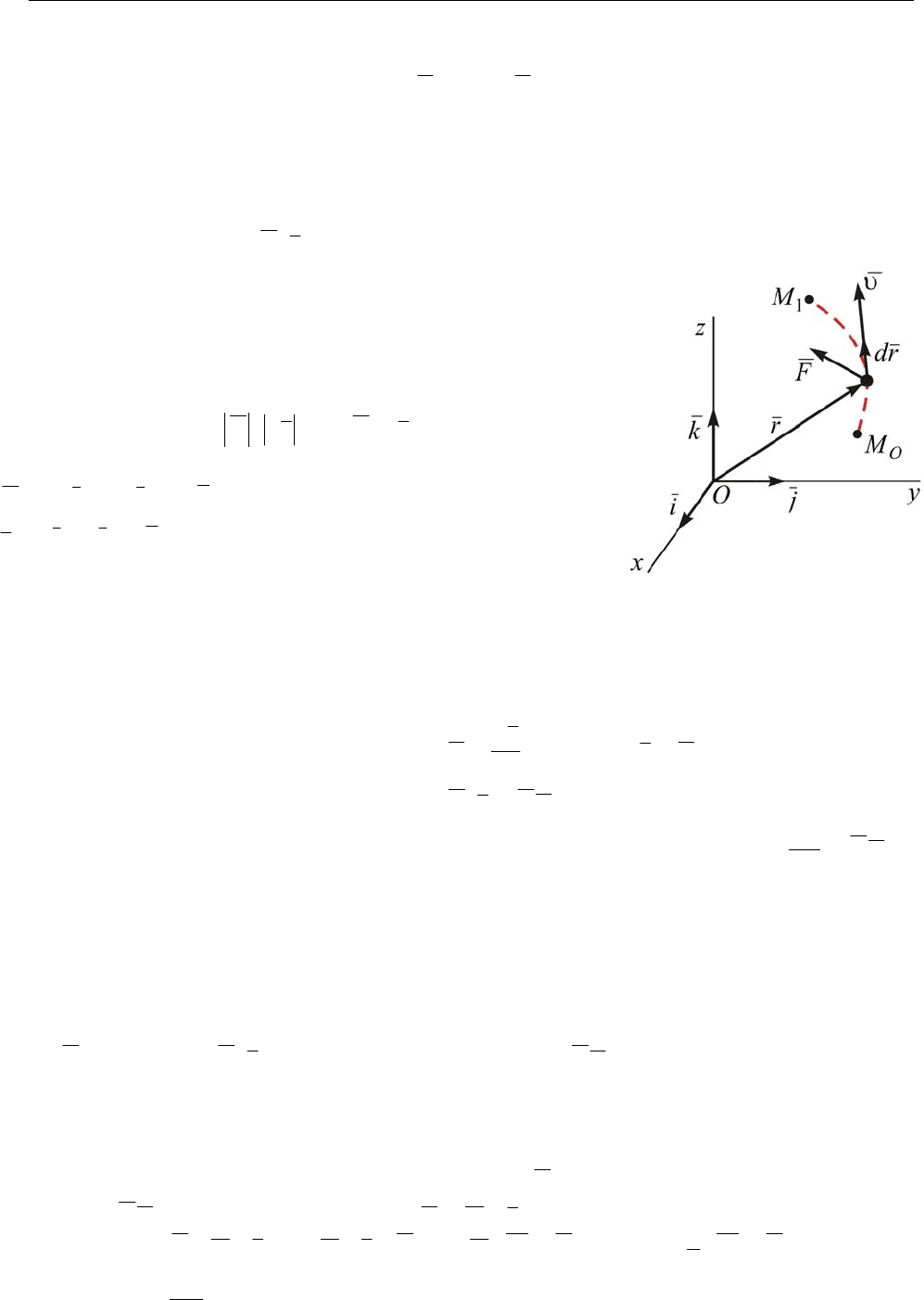
14.20. Элементарная и полная работа силы и момента силы. Элементарной
работой силы называется скалярное произведение вектора силы на вектор элемен-
тарного перемещения точки приложения силы (рис. 14.14):
r
dFdA = . (14.45)
Скалярное произведение векторов можно вы-
числить как произведение модулей перемножае-
мых векторов на косинус угла между ними. Тогда
получается следующая формула для вычисления
элементарной работы силы:
(
)
rdFrdFdA
∧
⋅⋅= cos .
Если известны разложения вектора силы
kFjFiFF
zyx
++=
и радиус-вектора
kzjyixr ++=
по базисным векторам, то скаляр-
ное произведение можно вычислить как сумму
попарных произведений координат и для элемен-
тарной работы силы получается формула, называемая аналитической:
dzFdyFdxFdA
zyx
+
+
=
. (14.46)
Может быть полезной ещё одна формула для вычисления элементарной работы
силы. Из определения вектора скорости
dt
rd
=
υ
следует d
t
r
d ⋅
=
υ
. Тогда
d
t
F
r
dFdA
υ
=
=
.
Мощностью силы называется производная работы по времени
υ
F
dt
dA
W == . Ха-
рактеризует быстроту совершения работы.
Работой силы (полной работой силы) на перемещении точки из положения
0
M в
положение
1
M
называется интеграл от элементарной работы силы вдоль криво-
линейной дуги
10
MM (рис. 14.14):
∫∫∫∫
=++===
1
0
1
0
1
0
1
0
)()(
t
t
M
M
zyx
M
M
M
M
dtFdzFdyFdxFrdFdAFA
υ
.
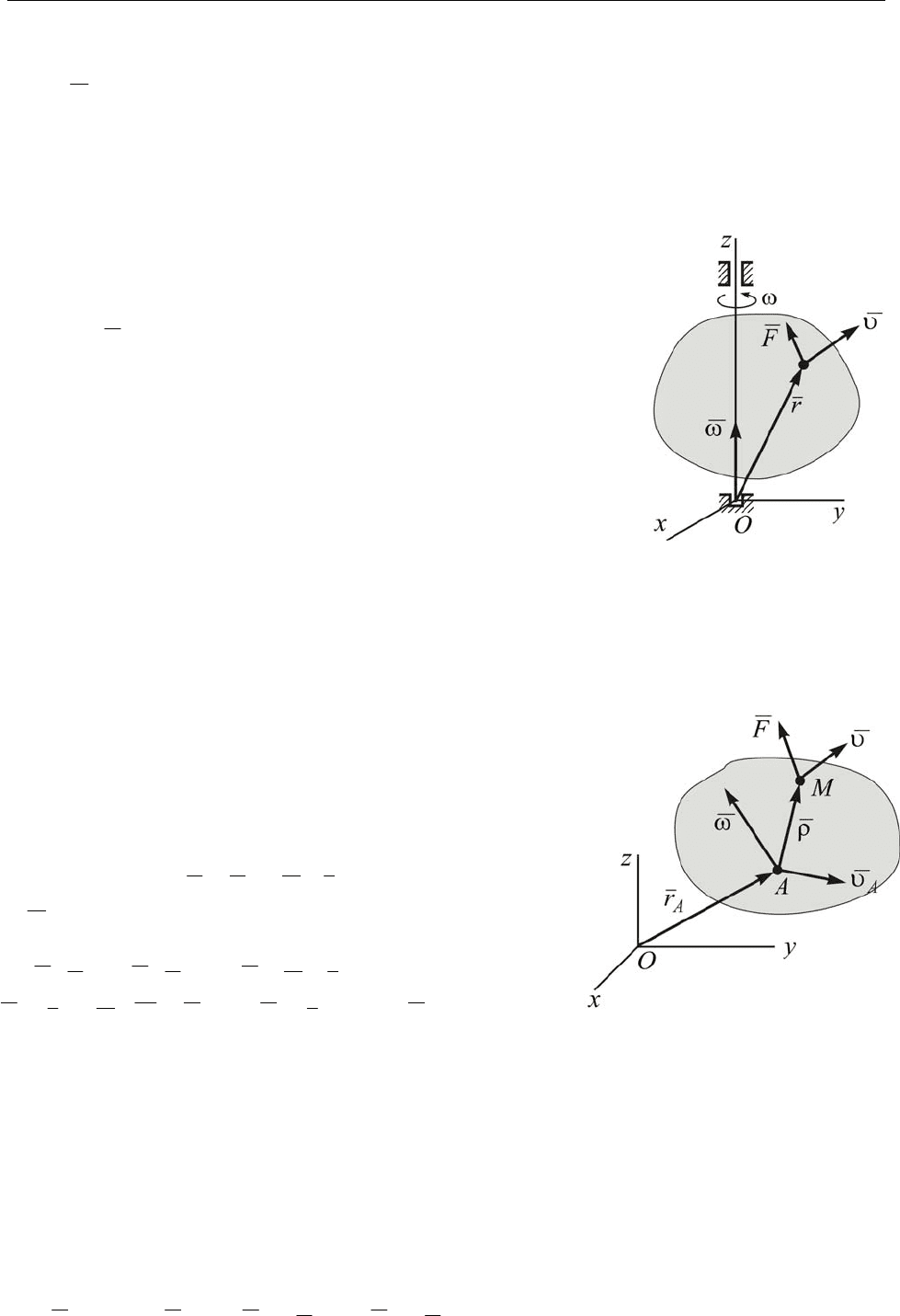
Получим, далее, формулу для вычисления элементарной и полной работы момен-
та силы. Пусть на некоторую точку твёрдого тела имеющего возможность вращать-
ся вокруг неподвижной оси Oz действует сила
F (рис. 14.15). Элементарная работа
силы
d
t
FdA
υ
= . По формуле Эйлера
r
×
=
ω
υ
. Тогда
()
(
)
=
⋅
⋅
=
⋅
=
×
⋅=×⋅= dtFMпрdtFMdtFrdtrFdA
OO
))(()(
ω
ω
ω
ω
ω
ϕ
ϕ
ωω
dMdtM
dt
d
=⋅⋅= .
Рис. 14.14
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
43
Здесь через
ω
M обозначена проекция векторного момента силы на направление
вектора
ω
угловой скорости.
Полученный результат может быть истолкован ещё и в такой форме. Действие
силы на твёрдое тело, имеющее возможность вращаться вокруг неподвижной оси,
характеризуется её вращающим действием, что количественно оценивается момен-
том этой силы. При повороте тела момент силы
z
M
совершает элементарную работу
ϕ
dMMdA
zz
=)( . (14.47)
Работа будет положительной, если направления мо-
мента
)(FM
z
и приращения угла
ϕ
d совпадают. В
противном случае работа отрицательна.
Работа момента силы
∫
=
1
0
)(
ϕ
ϕ
ϕ
dMMA
zz
. Если мо-
мент постоянен, то его можно вынести за знак инте-
грала и, для этого частного случая, получается форму-
ла
)()(
01
ϕ
ϕ
−=
zz
MMA .
14.21. Работа силы при свободном движении твёрдого тела. В кинематике бы-
ло доказано, что свободное движение твёрдого тела можно представить как сово-
купность поступательного движения вместе с
некоторой точкой называемой полюсом (точка
А
на рисунке 14.16) и сферического движения во-
круг полюса. В этом случае скорость произволь-
ной точки
M
складывается из переносной ско-
рости вместе с полюсом и относительной вокруг
полюса
r
А
×+
=
ω
υ
υ
,
где
ω
– вектор мгновенной угловой скорости
сферического движения. Тогда
=
×⋅+⋅=⋅= dtrFdtFdtFdA
A
)(
ω
υ
υ
ϕ
ω
ω
dFMrdFdtFMrdF
AAA
)()(
+
⋅=⋅+⋅= .
Таким образом, элементарная работа силы,
приложенной к точке твёрдого тела совершающего свободное движение, равна
сумме элементарных работ на элементарном поступательном перемещении вме-
сте с полюсом и элементарном вращательном перемещении вокруг мгновенной оси,
проходящей через полюс.
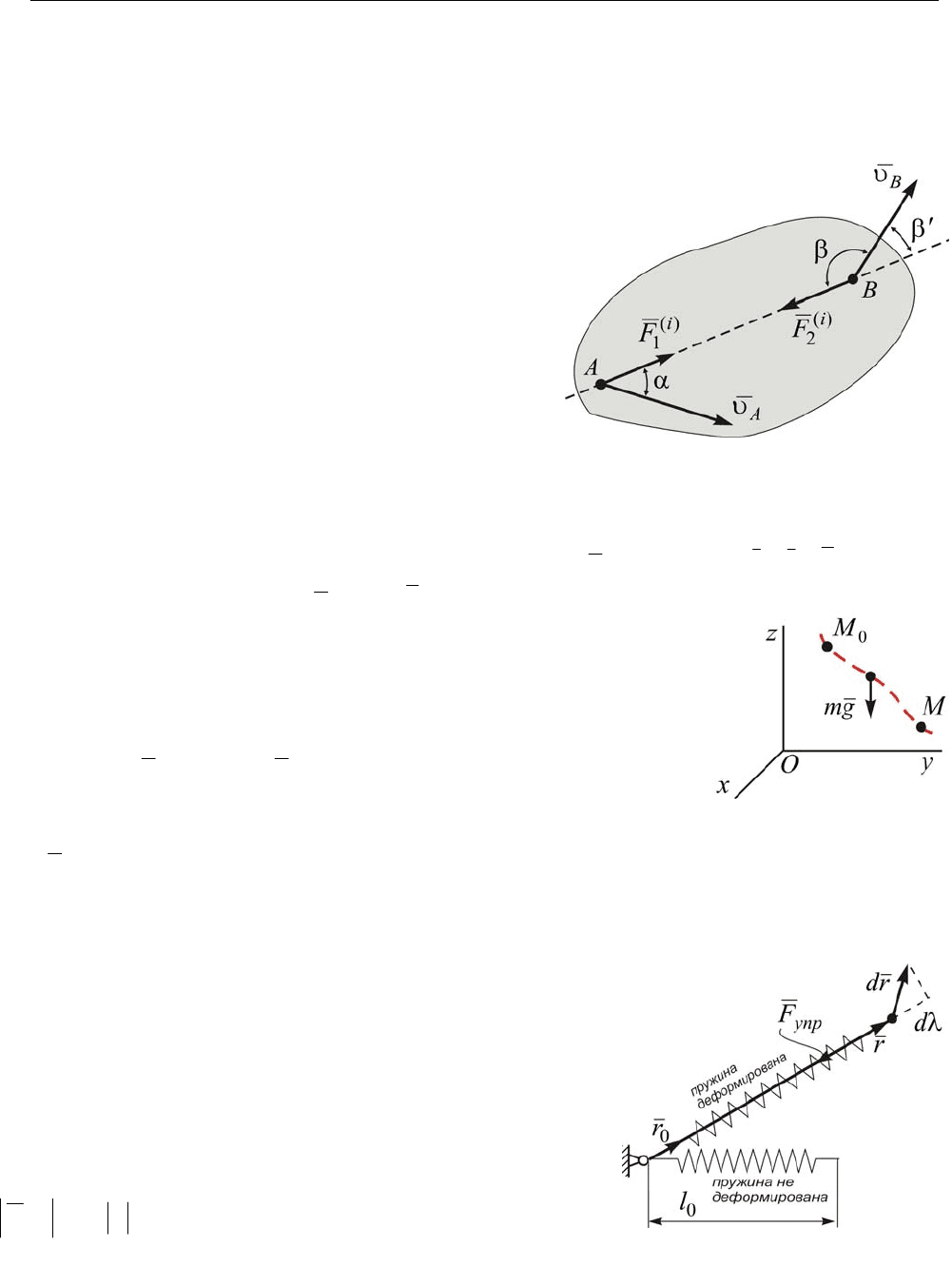
14.22. Работа внутренних сил твёрдого тела. Выделим в твёрдом теле
(рис.14.17) две произвольные точки и вычислим сумму элементарных работ сил
взаимодействия этих точек.
=+=⋅+⋅=+ dtFFdtFdtFFdAFdA
B
i
A
i
B
i
A
iii
)coscos()()(
)(
2
)(
1
)(
2
)(
1
)(
2
)(
1
βυαυυυ
Рис. 14.15
Рис. 14.16
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
44
dtFF
B
i
A
i
)coscos(
)(
2
)(
1
βυαυ
′
−=
. С учётом равенства модулей сил взаимодействия
двух точек, а также равенства проекций скоростей двух точек на ось, проходящую
через эти точки,
=
′
− dtFF
B
i
A
i
)coscos(
)(
2
)(
1
βυαυ
00)coscos(
)(
1
)(
1
=⋅⋅=
′
−= dtFdtF
i
BA
i
βυαυ
.
Следовательно, для сил взаимодействия
двух любых точек твёрдого тела сумма ра-
бот на всяком элементарном, следователь-
но, и конечном перемещении равна нулю.
А так как вся совокупность внутренних сил
разбивается на попарные силы действия и
противодействия, то и сумма работ всех
внутренних сил твёрдого тела равна нулю.
14.23. Работа силы тяжести. Если для системы координат Oxy
z
ось Oz напра-
вить вертикально вверх, то вектор силы тяжести
g
m
через орты i , j ,
k
осей коор-
динат запишется в виде
kmggm −= . Элементарная ра-
бота mgdzdzFdyFdxFdA
zyx
−=++= . Работа силы, при
перемещении точки из положения
0
M в положение
M
(рис. 14.18)
)()()(
0
00
zzmgmgdzgmdAgmA
z
z
M
M
−−=−==
∫∫
.
Часто этот результат записывают в форме
mgh
g
m
A
±=)(, где h – перепад высот (который считаем всегда положительным). В
последней формуле нужно взять знак «+», если материальная точка переместилась с
большей высоты на меньшую.
14.24. Работа силы упругости. Рассмотрим
пружину, работающую на растяжение (или сжа-
тие). Длину пружины в недеформированном со-
стоянии обозначим
0
l
. При изменении длины
такой пружины до значения
l
возникает сила
упругости, модуль которой, в соответствии с за-
коном Гука, вычисляется по формуле
λ
⋅= cF
упр
, где c - коэффициент жесткости,
)(
0
ll −=
λ
– деформация пружины.
Пусть длина деформации пружины изменена от значения
0
λ
до
λ
. Необходимо
вычислить работу, которую совершила сила упругости. Для этого рассмотрим пру-
жину в произвольном деформированном состоянии (рис. 14.19). Вектор силы упру-
Рис. 14.17
Рис. 14.18
Рис. 14.19
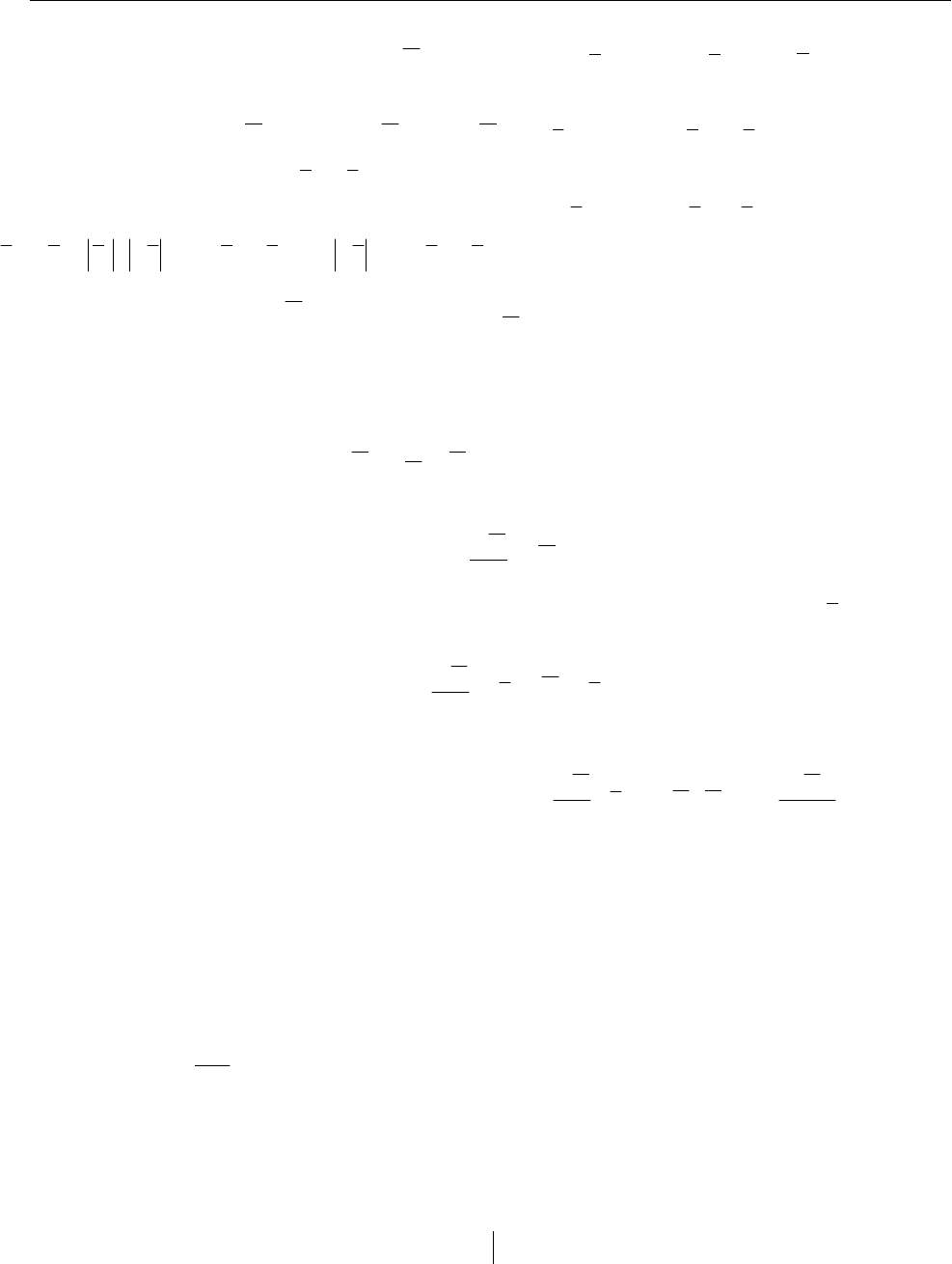
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
45
гости можно выразить формулой
000
)( rcrllcF
упр
⋅
⋅
−
=
−
⋅
−
=
λ
, где
0
r - орт радиус-
вектора точки приложения силы. Следовательно,
∫∫∫
⋅⋅⋅−=⋅== rdrcrdFFdAFA
упрупрупр
)()()(
0
λ
.
Скалярное произведение
rdr ⋅
0
равно элементарному удлинению
λ
d пружины при
изменении радиус-вектора от значения
r
до
r
d
r
+ . Действительно,
(
)
(
)
λ
drdrrdrdrrdrrdr =⋅⋅=⋅⋅=⋅
∧∧
0000
cos1cos . Тогда,
()
(
)
2
0
2
2
0
λλλλ
λ
λ
−−=−=
∫
c
dсFA
упр
. (14.48)
14.25. Теорема об изменении кинетической энергии точки. При движении точ-
ки её кинетическая энергия
2
2
1
)(
υυ
mT = , в общем случае, меняется. Какому закону
подчиняется это изменение? Для ответа на этот вопрос обе части уравнения
F
dt
d
m =
υ
,
выражающего второй закон Ньютона, умножим скалярно на вектор
r
d элементар-
ного перемещения точки:
rdFrd
dt
d
m ⋅=⋅
υ
. (14.49)
В правой части полученного равенства стоит элементарная работа силы, дейст-
вующая на точку. Преобразуем левую часть:
dT
m
ddmrd
dt
d
m =
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
==
2
2
υ
υυ
υ
. Сле-
довательно, уравнение (14.49) имеет вид
dAd
T
=
(14.50)
и выражает теорему об изменении кинетической энергии точки в дифференциаль-
ной форме:
дифференциал кинетической энергии точки равен элементарной работе
силы, действующей на точку
.
Если обе части уравнения (14.50) поделить на
d
t
, то получим ещё одну запись
той же теоремы:
W
dt
dT
= .
Проинтегрируем уравнение (14.50) вдоль траектории движения точки при её пе-
ремещении из положения
0
M в положение
M
∫∫
=
M
M
T
T
dAdT
00
, или
M
M
ATT
0
0
=− (14.51)
Уравнение (14.51) выражает теорему об изменении кинетической энергии точки в
интегральной форме:
изменение кинетической энергии точки равно работе силы,
действующей на точку
.

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
46
14.26. Теорема об изменении кинетической энергии механической системы.
На каждую точку механической системы действуют, в общем случае, равнодейст-
вующая внешних сил
)(e
k
F
и равнодействующая внутренних сил
)(i
k
F
. Тогда, урав-
нение (14.50) для произвольной точки можно записать в виде
)()(
2
)()(
2
i
k
e
k
kk
FdAFdA
m
d +=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
υ
,
N
k
...,,2,1
=
. (14.52)
Просуммировав это уравнение по всем точкам системы и вынося в левой части знак
дифференциала за знак суммы, получим
∑∑∑
===
+=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
N
k
i
k
N
k
e
k
N
k
kk
FdAFdA
m
d
1
)(
1
)(
1
2
)()(
2
υ
, или
∑∑
==
+=
N
k
i
k
N
k
e
k
FdAFdAdT
1
)(
1
)(
)()( . (14.53)
Формула (14.53) выражает теорему об изменении кинетической энергии механи-
ческой системы в дифференциальной форме:
дифференциал кинетической энергии
механической системы равен сумме элементарных работ всех внешних и внутрен-
них сил, действующих на систему
.
Поделив уравнение (14.53) на
d
t
, получим ещё одну запись той же теоремы:
∑∑
==
+=
N
k
i
k
N
k
e
k
FWFW
dt
dT
1
)(
1
)(
)()( .
Производная по времени от кинетической энергии системы равна сумме мощно-
стей всех внешних и внутренних сил, действующих на систему
.
Проинтегрируем каждое из уравнений (14.52) по соответствующей траектории и
после этого почленно просуммируем по всем точкам системы. Получим
∑∑
==
+=−
N
k
i
k
N
k
e
k
FAFATT
1
)(
1
)(
0
)()( . (14.54)
Уравнение (14.54) выражает теорему об изменении кинетической энергии меха-
нической системы в интегральной форме:
изменение кинетической энергии механи-
ческой системы при её перемещении из начального положения в конечное равно
сумме работ всех внешних и внутренних сил на этом перемещении
.
Потенциальное силовое поле
14.27. Потенциальное силовое поле и его войства. Силовым полем называется
часть пространства, в котором на материальную точку действует сила, завися-
щая от координат точки и времени
:
),,,( tzyxFF
=
.
Если сила явно не зависит от времени, то силовое поле называется стационар-
ным. В частном случае, сила может быть постоянной. Силовое поле в этом случае
называется однородным.

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
47
Стационарное силовое поле называется потенциальным, если существует та-
кая скалярная функция
),,( zy
x
U
, называемая силовой функцией, через которую
проекции силы на оси координат вычисляются по формулам
x
U
F
x
∂
∂
=
,
y
U
F
y
∂
∂
=
,
z
U
F
z
∂
∂
= . (14.55)
Эти три скалярных равенства можно записать в виде одного векторного
UgradF = , (14.56)
где
k
z
U
j
y
U
i
x
U
Ugrad
∂
∂
+
∂
∂
+
∂
∂
=
.
Как следует из определения (14.55), если вместо силовой функции ),,(
zy
x
U
взять
С
zy
x
U
+),,(, где
С
– любая постоянная, то значение силы не изменится. Ма-
тематики этот факт выражают так: силовая функция определяется с точностью до
аддитивной постоянной. Для инженеров и физиков, может быть, более ценным яв-
ляется иная формулировка этого свойства: начало отсчёта силовой функций можно
выбирать от любого положения механической системы.
Свойства потенциального силового поля. 1.
Элементарная работа силы
потенциального силового поля равна дифференциалу силовой функции:
dUdz
z
U
dy
y
U
dx
x
U
dzFdyFdxFdA
zyx
=
∂
∂
+
∂
∂
+
∂
∂
=++=
.
2. Работа силы потенциального силового поля равна разности значений силовой
функции в конечном и начальном положениях:
),,(),,(
000
00
zyxUzyxUdUdAA
M
M
M
M
−===
∫∫
. (14.57)
В частности, если начальная и конечная точки совпадают, то работа равна нулю.
3. Условие потенциальности силового поля выражается системой уравнений
0=
∂
∂
−
∂
∂
z
F
y
F
y
z
, 0=
∂
∂
−
∂
∂
x
F
z
F
zx
, 0=
∂
∂
−
∂
∂
y
F
x
F
x
y
.
Докажем первое из этих равенств. Согласно определению (14.55) имеем
yz
U
z
U
yy
F
z
∂∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
∂
∂
2
,
zy
U
y
U
zz
F
y
∂∂
∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
=
∂
∂
2
.
Для дважды дифференцируемой функции
U
, что предполагается, значение сме-
шанных производных не зависит от порядка дифференцирования. Поэтому, если по-
лученные равенства почленно вычесть, то убедимся, что
0=
∂
∂
−
∂
∂
z
F
y
F
y
z
. Аналогично
доказываются два других равенства.
14.28. Потенциальная энергия. Для потенциального поля сил наряду с силовой
функцией
U
используется так же несколько иная функция, характеризующая запас
энергии в данной точке силового поля, – потенциальная энергия
П
.
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
48
Потенциальной энергией потенциального силового поля в данной точке называ-
ется работа силы поля действующей на материальную точку при перемещении её
из данного положения
M
в начальное
0
M :
UUdUdAAП
M
M
M
M
M
M
−====
∫∫
0
00
0
Как видно из этого определения, потенциальная энергия с точностью до несуще-
ственной постоянной
0
U отличается от силовой функции лишь знаком.
14.29. Примеры вычисления силовой функции и потенциальной энергии.
Для однородного поля силы тяжести (рис. 14.16) mgd
z
dAd
U
−
=
=
. Следовательно,
1
CmgzdUU +−==
∫
, (14.58)
2
CmgzП
+
=
.
Для работы силы упругости пружины ранее была получена формула (14.48)
() ()
(
)
2
0
2
2
00
λλλλ
λ
λ
−−=−==
∫∫
c
dсFAdFA
упр
M
M
упр
.
Следовательно, для силовой функции справедлива формула
1
2
2
C
c
U
+−=
λ
, а для
потенциальной энергии
2
2
2
С
с
П +=
λ
. Здесь деформация пружины
λ
должна быть
выражена через координаты
x
, y , z . Если начало осей выбрано в положении, при
котором 0=
λ
, то
1
222
)(
2
Czyx
c
U +++−= ,
2
222
)(
2
Czyx
c
П +++= . (14.59)
14.30. Поверхности уровня силовой функции. Для привлечения языка рисун-
ков при изучении свойств потенциального силового поля вводится понятие поверх-
ности уровня силовой функции.
Поверхностью уровня силовой функции называется множество точек про-
странства, удовлетворяющее уравнению cons
t
C
zy
x
U
=
=
),,( .
Придавая постоянной
С
различные значения получим семейство поверхностей,
разбивающее пространство. По виду этих поверхностей и их взаимному расположе-
нию можно судить об особенностях потенциального поля. Этот анализ основан на
следующих свойствах.
Свойство 1. Сила, действующая на материальную точку со стороны поля, на-
правлена перпендикулярно поверхности уровня в сторону возрастания силовой
функции.
Свойство 2. Сила, действующая
на материальную точку со стороны поля, имеет
больший модуль в тех точках поля, где поверхности уровня расположены гуще
(ближе друг к другу).
Эти два свойства следуют из уравнения (14.56).

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
49
Свойство 3. Работа силы, действующей на материальную точку со стороны поля
равна нулю, если начальное и конечное положение точки расположены на одной и
той же поверхности уровня.
Последнее свойство следует из формулы (14.57) и определения поверхности
уровня силовой функции.
Для однородного поля силы тяжести поверхности уровня силовой функции, как
следует из (14.58), описываются уравнением
C
mg
z
=
−
, т.е. являются горизонталь-
ными плоскостями.
Из (14.59) следует, что для поля силы упругости поверхности уровня силовой
функции представляют собой концентрические сферы, так как описываются уравне-
нием Czyx =++
222
.
14.31. Закон сохранения механической энергии. Пусть на механическую сис-
тему действуют лишь потенциальные силы, т.е. силы, значение которых можно вы-
числить через силовую функцию по формулам
k
kx
x
U
F
∂
∂
= ,
k
ky
y
U
F
∂
∂
= ,
k
kz
z
U
F
∂
∂
= )...,,2,1(
N
k
=
По теореме об изменении кинетической энергии механической системы в диффе-
ренциальной форме
()
dUdz
z
U
dy
y
U
dx
x
U
dzFdyFdxFdT
N
k
k
k
k
k
k
k
N
k
kkzkkykkx
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
=++=
∑∑
== 11
Если перейти от силовой функции к потенциальной энергии, то последний ре-
зультат можно записать в виде 0)(
=
+
П
T
d , откуда следует, что
00
ПТПT
+
=
+
.
Левая часть полученного уравнения представляет полную механическую энер-
гию в конечном положении:
Е
П
Т
=
+
. Правая часть представляет полную механи-
ческую систему в начальном положении:
000
ЕПТ
=
+
. Следовательно, при движе-
нии механической системы лишь под действием потенциальных сил полная механи-
ческая энергия остаётся неизменной.
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
50
Глава 15. ПРИНЦИП ДАЛАМБЕРА
15.1. Принцип Даламбера. Сила инерции. Принцип Даламбера сформулирован
в 1743 г. и первоначально, в отличие от законов Ньютона, был предназначен для
изучения движения несвободных механических систем. В настоящее время этот
принцип и вытекающий из него метод кинетостатики рассматривают как удобный
приём, позволяющий дифференциальные уравнения динамики сводить к форме
уравнений равновесия статики.
Рассмотрим, вначале, этот принцип применительно
к точке. В соответствии с ак-
сиомами динамики основное уравнение движения материальной точки имеет вид
R
F
am
+
=
, (15.1)
где
F - равнодействующая активных сил;
R
- равнодействующая реакций связей;
2
2
d
t
rd
a = - абсолютное ускорение точки.
Уравнение (15.1) можно также записать в виде
(
)
0
=
−
+
+
amRF .
Слагаемое
()
am− обозначают
Φ
и называют даламберовой силой инерции (или
просто силой инерции). Основное уравнение динамики материальной точки при ис-
пользовании силы инерции принимает следующий вид:
0
=
Φ
+
+
R
F . (15.2)
Так как указанные выше силы образуют систему сходящихся сил, то уравнение
(15.2) можно рассматривать как условие равновесия системы сил
()
Φ
,, RF . В этом
и состоит принцип Даламбера для материальной точки. Формулируется он так: при
движении материальной точки в любой момент времени приложенные к ней ак-
тивные силы и реакции связей вместе с силой инерции образуют систему сил, экви-
валентную нулю (уравновешенную систему сил), т. е.
(
)
Φ
,, RF ഗ 0 (15.3)
Отметим, что в формулировке принципа Даламбера речь идёт об уравновешен-
ности определённой системы сил, а не о равновесии (покое) материальной точки.
Таким образом, дополняя систему активных сил и реакций связей, приложен-
ных к точке, силой инерции, получаем уравновешенную систему сходящихся сил,
для которой должно выполняться условие (15.2). В проекциях на
оси декартовой
системы координат имеем:
0=Φ++
xxx
RF ; 0
=
Φ
+
+
yyy
RF ; 0=Φ
+
+
zzz
RF ,
где
xm
x
&&
−=Φ
, ym
y
&&
−
=Φ .
zm
z
&&
−
=Φ
.
15.2. Принцип Даламбера для механической системы. Рассмотрим механиче-
скую систему, состоящую из
N
материальных точек. Применяя принцип Даламбера
к каждой точке системы, получаем
0
=
Φ
+
+
kkk
RF
,
N
k
...,,2,1
=
, (15.4)
