Винокуров В.Н. Лекции по теоретической механике
Подождите немного. Документ загружается.

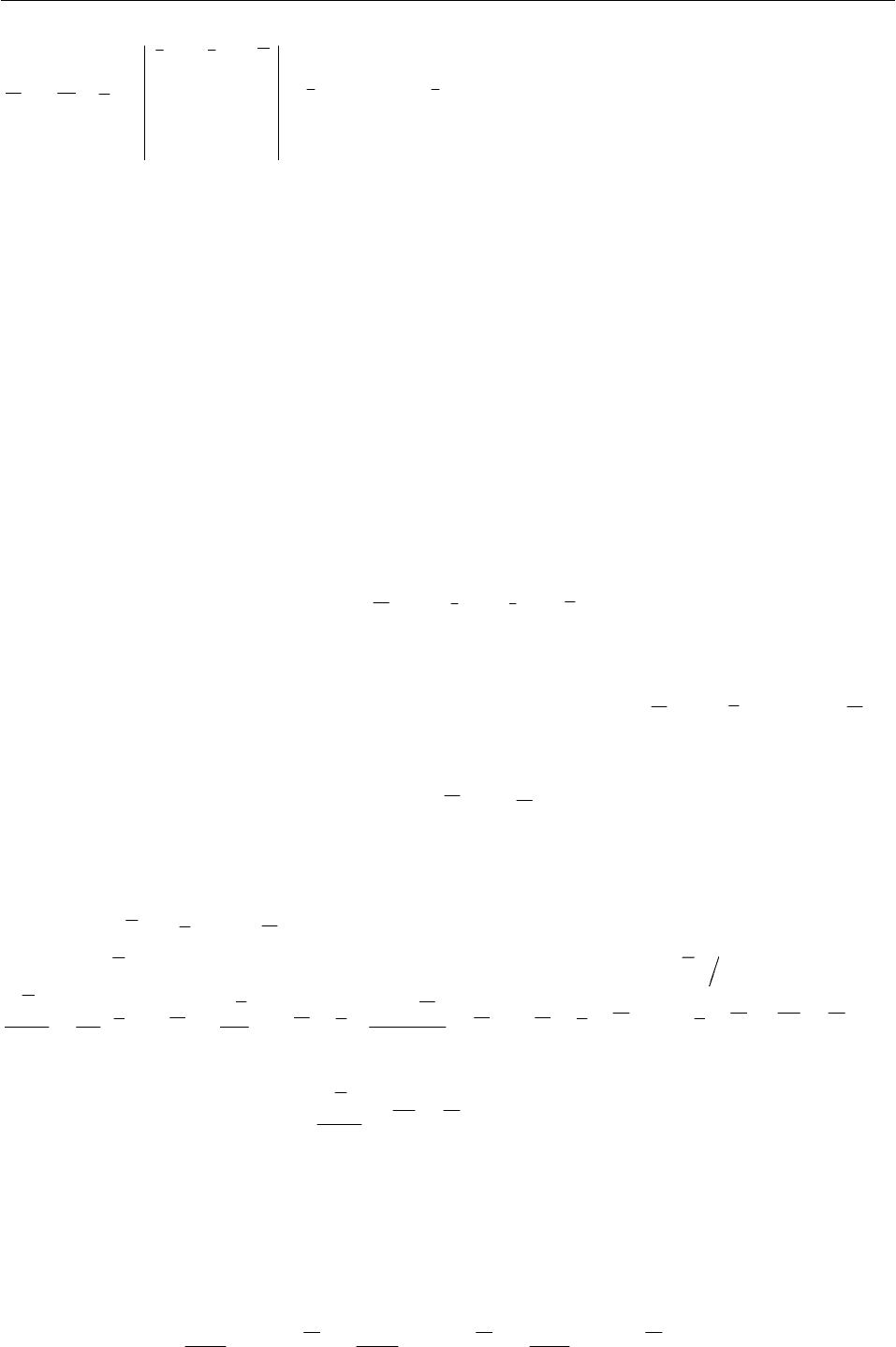
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
31
)()(00
kzkz
kkk
zkk
xjyi
zyx
kji
r
ωωωωυ
+−==×= .
Следовательно, проекции вектора скорости точки на оси Ox и O
y
вычисляются по
формулам
kzkxk
yx
ω
υ
−
==
&
,
kzkyk
xy
ω
υ
=
=
&
. Тогда
[]
=
−
−= )()(
kzkkzkkz
yyxxmk
ω
ω
)(
22
kkkz
yxm +
ω
. (14.24)
Геометрический смысл величины )(
22
kk
yx + – квадрат расстояния от точки
k
A до
оси вращения Oz :
222
kkk
yxR += .
Просуммировав выражения (14.24) по всем точкам, получим
zz
N
k
kkz
N
k
kkzz
JRmRmK
ωωω
===
∑∑
== 1
2
1
2
, где величина
∑
=
=
N
k
kkz
RmJ
1
2
– момент инер-
ции тела относительно оси Oz . Окончательно имеем
zzz
JK
ω
=
. (14.25)
Знак величины
z
K определяется знаком проекции угловой скорости
z
ω
.
Замечание. Следует обратить внимание, что в данной механической системе вектор кинетиче-
ского момента относительно центра
O kKjKiKK
zyxO
++= . не направлен по оси вращения те-
ла. Проекции кинетического момента на оси
Ox и Oy , как будет доказано ниже, вычисляются в
рассматриваемой задаче по формулам:
zzxx
JK
ω
−
=
,
zyzy
JK
ω
−
=
. И лишь в случае если ось Oz –
главная ось инерции, то
0==
zxyz
JJ
и, следовательно,
0
=
=
yx
KK
, kKK
zO
= и вектор
O
K ока-
жется направленным вдоль оси вращения. В этом частном случае для вектора кинетического мо-
мента будет справедливой формула
ω
zO
JK = . (14.26)
14.11. Теорема об изменении момента количества движения материальной
точки.
Момент количества движения точки величина переменная, что вытекает из
определения
)()( tmtrk
O
υ
×= . Выведем уравнение, которому подчиняется измене-
ние вектора
O
k , для чего вычислим производную по времени dtkd
O
:
()
)(0
)(
FMFrFrm
d
t
md
rm
d
t
rd
mr
d
t
d
d
t
kd
O
O
=×+=×+×=×+×=×=
υυ
υ
υυ
.
Таким образом, получили
)(FM
dt
kd
O
O
= (14.27)
Уравнение (14.27) выражает теорему об изменении момента количества движе-
ния материальной точки: производная по времени от момента количества движе-
ния точки относительно неподвижного центра O равна векторному моменту рав-
нодействующей силы относительно того же центра O .
В проекциях на декартовы оси координат
)(FM
dt
dk
x
x
= , )(FM
dt
dk
y
y
= , )(FM
dt
dk
z
z
= . (14.28)

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
32
14.12. Теорема об изменении кинетического момента механической системы.
Рассмотрим механическую систему, состоящую из
N
материальных точек, и для
каждой из них запишем теорему об изменении момента количества движения отно-
сительно неподвижного центра O :
)()(
)(
i
k
k
e
k
kkkk
FrFrmr
dt
d
×+×=×
υ
(
N
k
...,,2,1
=
). (14.29)
Здесь
)(e
k
F
– равнодействующая всех внешних, а
)(i
k
F
– равнодействующая всех
внутренних сил действующих на k – ю точку.
Просуммируем равенства (14.29) по всем точкам
∑∑∑
===
×+×=×
N
k
i
k
k
N
k
e
k
k
N
k
kkk
FrFrmr
dt
d
1
)(
1
)(
1
)(
υ
.
Проанализируем полученное уравнение. В левой его части стоит производная по
времени от кинетического момента механической системы вычисленного относи-
тельно неподвижного центра O . Действительно,
O
N
k
kkk
N
k
kkk
K
dt
d
mr
dt
d
mr
dt
d
=×=×
∑∑
== 11
)()(
υυ
. Первое слагаемое в правой части есть
главный момент всех внешних сил:
)(
1
)(
1
)(
)(
e
O
N
k
e
k
O
N
k
e
k
k
LFMFr ==×
∑∑
==
. Второе слагае-
мое в правой части равно нулю по свойству внутренних сил. Поэтому уравнение
можно записать в виде
∑
=
=
N
k
e
k
O
O
FM
dt
Kd
1
)(
)( (14.30)
и выражает оно теорему об изменении кинетического момента механической систе-
мы: производная по времени от кинетического момента относительно неподвиж-
ного центра O равна главному моменту внешних сил относительно того же цен-
тра O .
В проекциях на оси координат
∑
=
=
N
k
e
k
x
x
FM
dt
dK
1
)(
)(,
∑
=
=
N
k
e
k
y
y
FM
dt
dK
1
)(
)(,
∑
=
=
N
k
e
k
z
z
FM
dt
dK
1
)(
)( . (14.31)
14.13. Законы сохранения кинетического момента. 1. Если главный момент
внешних сил равен нулю,
0)(
1
)()(
==
∑
=
N
k
e
k
O
e
O
FML , то из уравнения (14.30) следует,
что вектор кинетического момента не меняется
constK
O
= .
Это векторное равенство эквивалентно трём скалярным
1
CK
x
= ,
2
CK
y
= ,
3
CK
z
=
. (14.32)
Пример. Рассмотрим движение планеты (например, Земля) под
действием силы гравитации
G к Солнцу, считая его неподвижным
(рис. 14.5) и пренебрегая притяжением других планет. В этом случае
Рис. 14.5

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
33
момент силы притяжения относительно центра O
0)( =×= GrGM
O
так как перемножаемые
векторы коллинеарны и, следовательно, имеет место только что рассмотренный закон сохранения
кинетического момента. Уравнения (14.32), с учётом (14.21), запишем в виде
1
)( Cyzzym
=
−
&
&
,
2
)( Czxxzm
=
−
&
&
,
3
)( Cxyyxm
=
−
&&
.
Если первое из полученных уравнений умножить на
x
, второе на y и третье на
z
и после это-
го почленно сложить, то придём к соотношению
zCyCxC
321
0
+
+
=
, из которого следует, что
движение планеты будет происходить в неподвижной плоскости проходящей через Солнце.
2. Может случиться, что главный момент внешних сил относительно центра O не
равен нулю, но равна нулю его проекция на одно из направлений, например, на-
правление оси Oz . Тогда из (14.31) следует, что constK
z
=
.
Пример. Скамья Жуковского представляет диск, который достаточно легко может вращаться
вокруг неподвижной вертикальной оси (оси
Oz на рисунке 14.6). Исследователь встаёт на диск,
разводит руки в стороны и ему сообщается угловая скорость
0
ω
. Затем исследователь руки опус-
кает, максимально прижимая их к туловищу. При этом угловая ско-
рость вращения
ω
заметно возрастает:
0
ω
ω
> . Необходимо объяс-
нить данный эффект.
Решение. Внешним силами, действующие на систему иссле-
дователь–диск, являются силы тяжести и реакция
O
R подпятника
O
. Момент каждой из указанных сил относительно оси
Oz
равен
нулю. Следовательно, имеет место закон сохранения
1
CK
z
=
.
По формуле (14.25), для твёрдого тела, вращающегося вокруг
неподвижной оси
Oz
, проекция кинетического момента на ось
вращения равна произведению осевого момента инерции на угло-
вую скорость вращения:
zzz
JK
ω
= . В начальном положении, когда
руки разведены в стороны, момент инерции, обозначим его
0z
J ,
максимален. Когда же руки прижаты к туловищу, то момент инер-
ции
z
J минимален. По закону сохранения
zzzz
JJ
ω
ω
=
00
, откуда
следует
0
0
0 z
z
z
zz
J
J
ωωω
>= , так как 1
0
>
z
z
J
J
.
14.14. Дифференциальное уравнение вращательного движения твёрдого тела
вокруг неподвижной оси.
Как известно из кинематики, положение твёрдого тела
при его вращательном движении вокруг неподвижной оси определяется одной ко-
ординатой – углом поворота
ϕ
вокруг этой оси (рис. 14.7).
При вращении тела под действием сил и моментов угол
поворота меняется.
Какому уравнению (какому закону) подчиняется изме-
нение угла поворота?
Для вывода такого уравнения воспользуемся теоремой
об изменении кинетического момента системы в проекции
на ось вращения Oz (14.31):
∑
=
=
N
k
e
k
z
z
FM
dt
Kd
1
)(
)(. Для твёр-
дого тела, вращающегося вокруг неподвижной оси враще-
Рис. 14.7
Рис. 14.6
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
34
ния, кинетический момент в проекции на эту ось
zzz
JK
ω
=
, где осевой момент
инерции constJ
z
= . Тогда указанную выше теорему можно записать в виде
∑
=
=
N
k
e
k
zz
FMJ
1
)(
)(
ϕ
&&
. (14.33)
Уравнение (14.33) есть уравнение вращательного движения твёрдого тела вокруг
неподвижной оси.
Пример. Однородный диск массы кг 4
=
m и радиу-
са
м 2,0=r
может свободно (без трения) вращаться во-
круг неподвижной оси
Oz совпадающей с осью сим-
метрии диска (рис. 14.8). К вращающемуся с угловой
скоростью
-1
0
с 2=
ω
диску прикладывают пару сил с
моментом
Нм 1,0 tM
z
=
.
Найти кинематическое уравнение движения
)(t
ϕ
ϕ
= .
Массой вала, удерживающего диск, пренебречь. В начальном положении угол поворота диска
принять равным нулю.
Решение. Рассмотрим вращательное движение твёрдого тела диск–вал и укажем действие на
него внешних сил и моментов: пара сил с моментом
z
M
, сила тяжести
g
m , реакция
A
R подшип-
ника A и реакция
B
R подшипника
B
. Момент каждой из сил
g
m ,
A
R ,
B
R относительно оси Oz
равен нулю. Следовательно, с учётом того, что для диска момент инерции
2
2
mr
J
z
= , дифференци-
альное уравнение (14.33) вращательного движения твёрдого вокруг неподвижной оси в данной за-
даче можно
записать в виде
z
M
mr
=
ϕ
&&
2
2
. После подстановки числовых значений и сокращений,
получим t25,1=
ϕ
&&
.
Следующим шагом в решении задачи является интегрирование полученного дифференциаль-
ного уравнения:
t
dt
d
25,1=
ω
⇒ tdtd 25,1
=
ω
⇒
1
25,1 Ctdtd +=
∫
∫
ω
⇒
1
2
2
25,1 C
t
+=
ω
⇒
1
2
2
25,1 C
t
dt
d
+=
ϕ
⇒ dtC
t
d )
2
25,1(
1
2
+=
ϕ
⇒
21
2
)
2
25,1( CdtC
t
d ++=
∫∫
ϕ
⇒
21
3
6
25,1 CtC
t
++=
ϕ
.
Запишем соотношения
1
2
2
25,1 C
t
+=
ω
и
21
3
6
25,1 CtC
t
++=
ϕ
в начальном положении твёрдо-
го тела:
⎩
⎨
⎧
++=
+=
.000
,02
2
1
С
С
Следовательно, произвольные постоянные интегрирования имеют значения
2
1
=С , 0
2
=
С и угол
поворота диска изменяется по закону
t
t
2
6
25,1
3
+=
ϕ
.
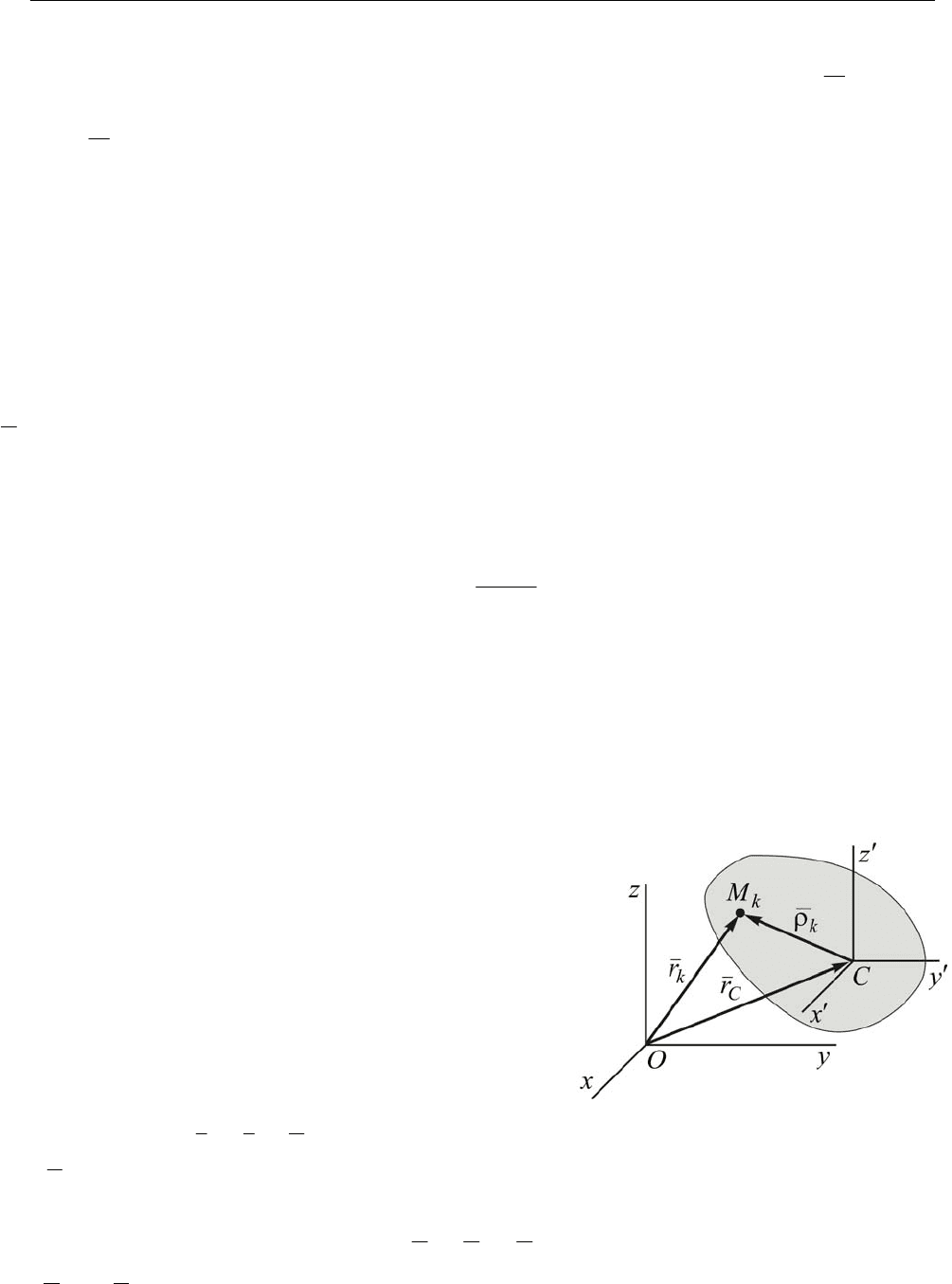
14.15. Кинетический момент механической системы при сложном её движе-
нии.
Рассмотрим движение некоторой совокупности материальных точек относи-
тельно неподвижной системы отсчёта Oxy
z
(рис. 14.9). Введём в рассмотрение ещё
Рис. 14.8
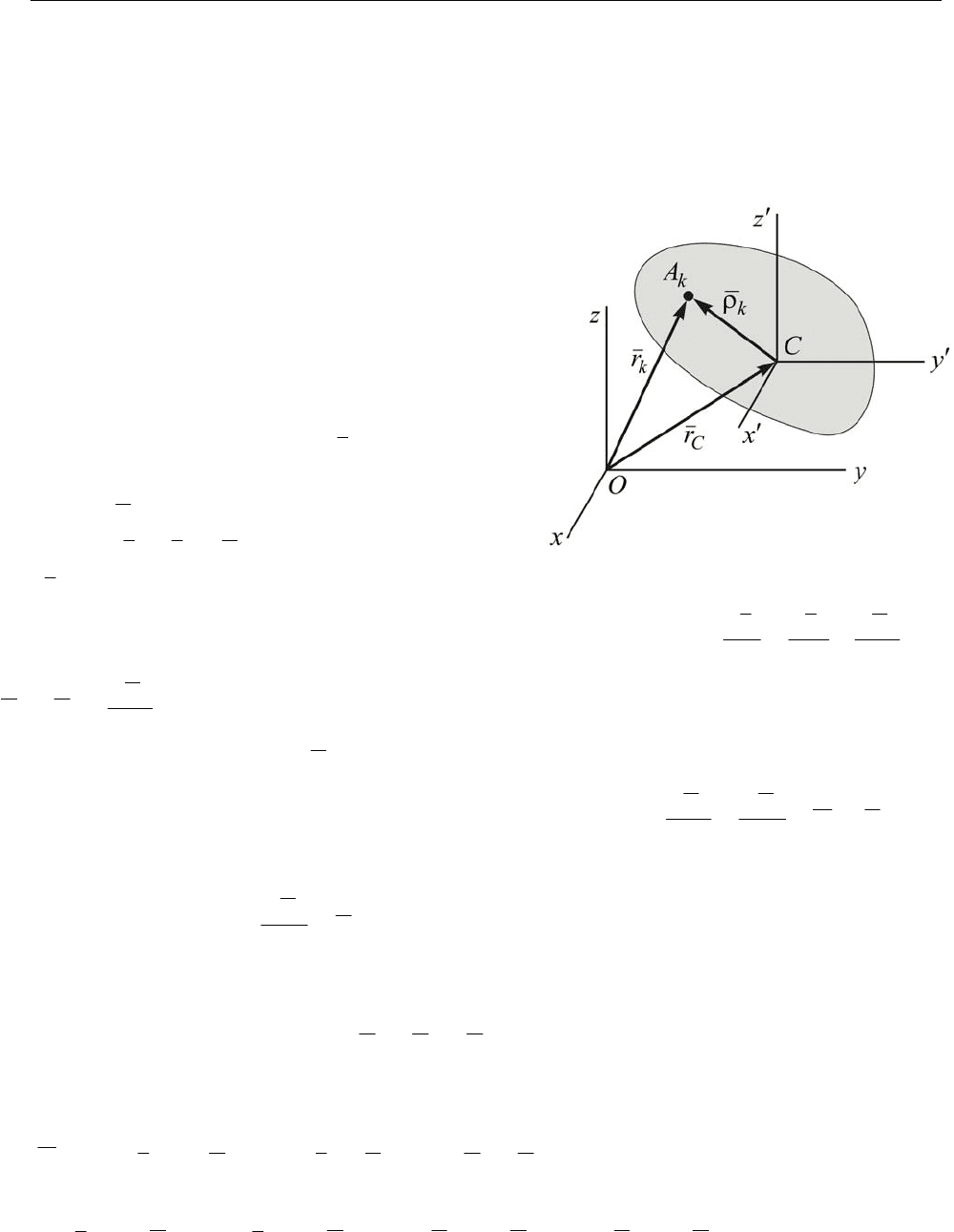
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
35
одну систему координат zyxC
′
′′
с началом в центре масс механической системы и
осями параллельными соответствующим осям неподвижной системы координат. В
этом случае система отсчёта zyxC
′
′
′
будет совершать поступательное движение и на-
зывают её кёниговой системой отсчёта.
Можно вычислить кинетический мо-
мент механической системы относитель-
но неподвижного центра O и относи-
тельно подвижного центра масс
C
. Нас
будет интересовать связь между этими
величинами.
Положение произвольной точки
k
A
относительно неподвижного центра оп-
ределим радиус-вектором
k
r , относи-
тельно подвижного центра масс радиус-
вектором
k
ρ
. Очевидно соотношение
kCk
rr
ρ
+= , (14.34)
где
C
r – радиус-вектор центра
C
.
Вычислим производную по времени от равенства (14.33)
dt
d
dt
rd
dt
rd
kCk
ρ
+= , или,
dt
d
k
Ck
ρ
υυ
+= .
Так как радиус-вектор
k
ρ
задан в подвижной системе координат, то производ-
ную от этого вектора нужно вычислять по формуле Бура:
ke
kk
dt
d
dt
d
ρω
ρρ
×+=
~
. Здесь
локальная производная определяет скорость движения точки относительно подвиж-
ной системы отсчёта,
r
k
k
dt
d
υ
ρ
=
~
, а угловая скорость
e
ω
поворота подвижных осей,
движущихся поступательно, равна нулю. Следовательно, имеем следующее соотно-
шение между векторами скоростей
r
kCk
υυυ
+= . (14.35)
Подставим соотношения (14.34) и (14.35) в формулу (14.22) для кинетического
момента системы относительно неподвижного центра O и преобразуем её.
[]
=+×+=×=
∑∑
==
N
k
r
kCkkC
N
k
kkkO
mrmrK
11
)()()(
υυρυ
∑∑∑∑
====
×+×+×+×
N
k
r
kkk
N
k
Ckk
N
k
r
kkC
N
k
CkC
mmmrmr
1111
)()()()(
υρυρυυ
.
Упростим, насколько возможно, каждое из слагаемых правой части последнего
выражения.
Рис. 14.9

В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
36
Первое слагаемое:
CCC
N
k
kC
N
k
CkC
Mrmrmr
υυυ
×=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
×=×
∑∑
== 11
)(. Здесь
∑
=
=
N
k
k
mM
1
– масса всей системы.
Второе слагаемое:
0
~
~
)(
11
=×=×=×
∑∑
==
CC
N
k
kkC
N
k
r
kkC
M
dt
d
rm
dt
d
rmr
ρρυ
. Здесь 0
=
C
ρ
,
так как начало отсчёта подвижной системы координат взято в центре масс системы.
По той же причине обращается в нуль третье слагаемое:
00)(
11
=×=×=×
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=×
∑∑
==
СCCC
N
k
kk
N
k
Ckk
Mmm
υυρυρυρ
.
Четвёртое слагаемое не упрощается, так как все сомножители зависят от индекса
суммирования
k
. Следовательно, это есть определение некоторой физической вели-
чины. А именно, так вычисляется кинетический момент системы относительно под-
вижного центра масс, который обозначим
r
C
K .
Окончательно приходим к следующему результату:
r
CCCO
KMrK +×=
υ
. (14.36)
Кинетический момент системы при сложном её движении равен моменту коли-
чества движения центра масс, считая, что в нём сосредоточена масса всей сис-
темы, плюс кинетический момент относительно подвижного центра масс.
Пример. По неподвижному горизонтальному рельсу катится без проскальзывания однородный
диск массы
кг 2=
M
и радиуса м 6,0=R . Скорость центра масс диска см 4=
С
υ
.
Вычислить кинетический момент диска относительно произвольной точки рельса.
Решение. Введём в рассмотрение две правых прямоугольных системы координат, непод-
вижную
Oxyz с началом в произвольной точке О рельса и поступательно движущуюся zyxС
′
′
′
с
началом центре масс
С диска (рис. 14.10). В этом случае оси Oz и zC
′
будут направлены перпен-
дикулярно плоскости рисунка (на нас).
Диск совершает сложное движение, а именно плоское, состоящее из поступательного вместе с
центром масс
С и вращательного вокруг оси zС
′
. Потому для вычисления кинетического момента
диска воспользуемся формулой (14.36).
Вектор
CC
Mr
υ
× направлен в положительном на-
правлении оси
Oz
а его модуль
скгм 8,4sin
2
==⋅⋅=×
CCCCC
MRMrMr
υαυυ
, так
как
Rr
C
=
α
sin .
Определим вектор
r
C
K . Относительным движением
диска по отношению к подвижным осям
zyxС
′
′
′
будет
его вращение в положительном направлении вокруг
оси
zС
′
. Поэтому, кинетический момент относительно-
го движения
r
C
K нужно вычислять как кинетический
момент твёрдого тела вращающегося как бы вокруг неподвижной оси
zС
′
совпадающей с осью
материальной симметрии диска. В этом случае
ω
z
r
C
JK = (см. формулу 14.26). Здесь вектор угло-
вой скорости
ω
направлен в положительном направлении оси zС
′
или, всё равно, что оси Oz , по
модулю равен
R
С
υ
, а 2
2
MRJ
z
= . Следовательно, направлен вектор
r
C
K в положительном на-
Рис. 14.10
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
37
правлении оси
Oz
и по модулю 2
C
r
C
MRK
υ
= . Окончательно приходим к выводу, что направлен
вектор кинетического момента диска в положительном направлении оси
Oz и по модулю равен
C
MR
υ
2
3
.
14.16. Теорема об изменении кинетического момента относительно подвиж-
ного центра масс.
Ранее было получено уравнение (14.30), определяющее закон из-
менения кинетического момента относительно неподвижного центра
. Но, как уви-
дим ниже, для решений задач динамики важным является также знание закона, ко-
торому удовлетворяет изменение кинетического момента относительно подвижного
центра масс системы. К выводу такого уравнения сейчас приступаем.
Итак, рассмотрим движение механической системы состоящей из точек
1
A ,
2
A ,
…,
N
A
массы которых соответственно равны
1
m
,
2
m
, …,
N
m
. Введём в рассмотре-
ние две системы отсчёта, неподвижную Oxy
z
и подвижную zyxC
′′′
с началом в цен-
тре масс системы и осями параллельными соответствующим неподвижным осям.
Для геометрической иллюстрации наших рассуждений будем использовать рисунок
14.9.
В уравнении, выражающем теорему об изменении кинетического момента отно-
сительно неподвижного центра O
(
)
∑
=
×=
N
k
e
k
k
O
Fr
dt
Kd
1
)(
,
заменим
O
K согласно (14.36) и
k
r согласно (14.34)
()
()
[]
∑
=
×+=+×
N
k
e
k
kC
r
CCC
FrKMr
dt
d
1
)(
ρυ
и раскроем скобки:
∑∑
==
×+×=+×+×
N
k
e
k
k
N
k
e
k
C
r
CC
CC
C
FFr
dt
Kd
dt
dM
rM
dt
rd
1
)(
1
)(
ρ
υ
υ
. (14.37)
В полученном выражении:
0=×=×
CCC
C
MM
dt
rd
υυυ
как векторное произведе-
ние коллинеарных векторов;
∑
=
×=×
N
k
e
k
C
C
C
Fr
dt
dM
r
1
)(
υ
с учётом теоремы о движении
центра масс механической системы;
∑∑
==
×=×
N
k
e
k
C
N
k
e
k
C
FrFr
1
)(
1
)(
– не зависящая от ин-
декса суммирования величина
C
r вынесена за знак суммы;
∑∑
==
=×
N
k
e
k
C
N
k
e
k
k
FMF
1
)(
1
)(
)(
ρ
– по определению векторного момента силы относитель-
но центра
C
.
Тогда, уравнение (14.37) преобразуется к виду
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
38
∑
=
=
N
k
e
k
C
r
C
FM
dt
Kd
1
)(
)( . (14.38)
В проекции на оси подвижной системы координат
(
)
()
()
.
,
,
)(
1
)(
1
)(
1
e
k
N
k
zC
r
zC
e
k
N
k
yC
r
yC
e
k
N
k
xC
r
xC
FM
dt
dK
FM
dt
dK
FM
dt
dK
∑
∑
∑
=
′
′
=
′
′
=
′
′
=
=
=
(14.39)
Уравнение (14.38) выражает теорему об изменении кинетического момента отно-
сительно подвижного центра масс: производная по времени от вектора кинетиче-
ского момента системы, вычисленного в кёниговой системе отсчёта, равна век-
торной сумме моментов всех внешних сил относительно центра масс.
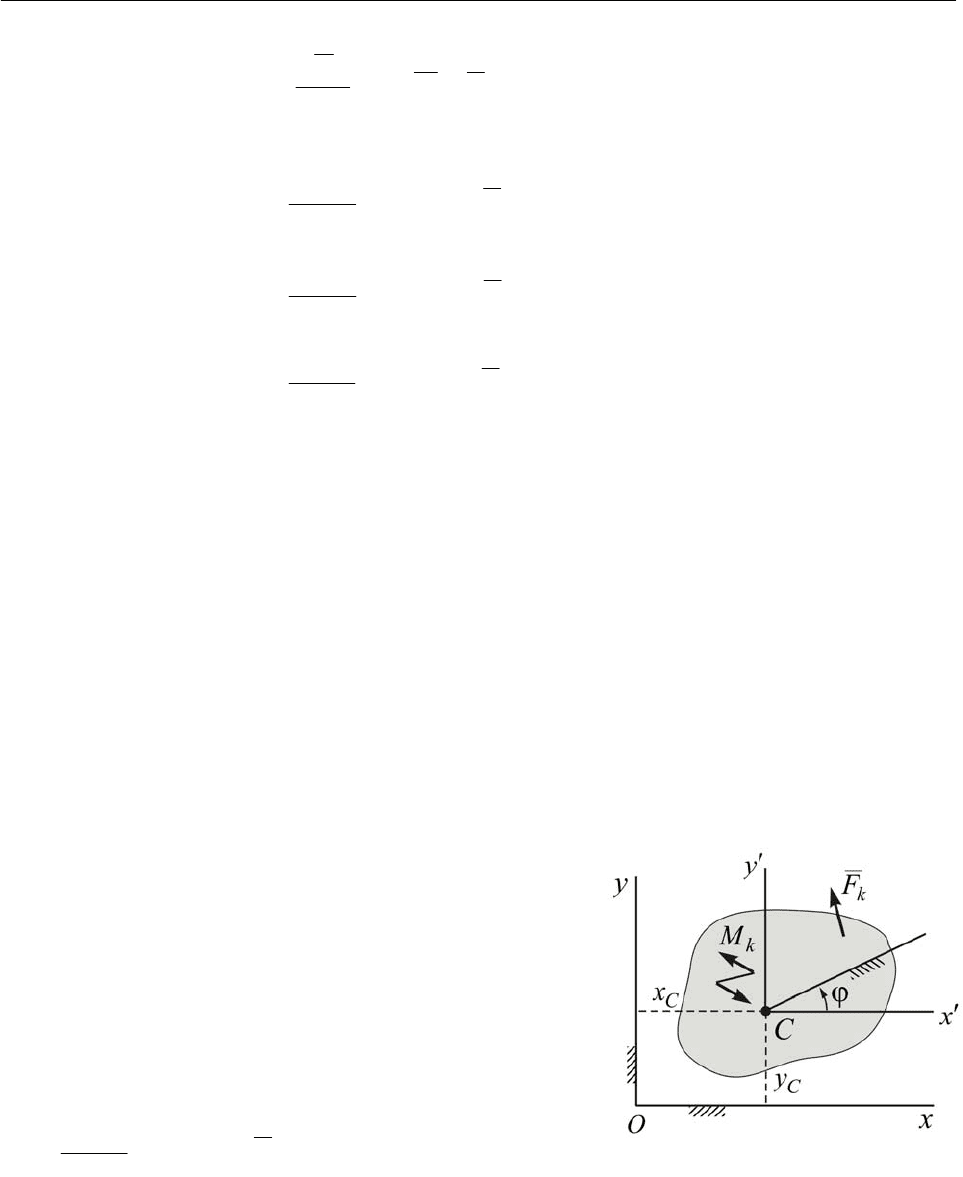
14.17. Дифференциальные уравнения плоского движения твёрдого тела. Оп-
ределим положение твёрдого тела при плоском его движении координатами
C
x ,
C
y ,
определяющими положение центра масс
С
тела, и углом поворота
ϕ
, определяю-
щем поворот тела вокруг центра масс (рис. 14.11). При движении тела эти координа-
ты меняются. Каким уравнениям подчиняется их изменение?
По теореме о движении центра масс системы в проекции на оси O
x
и O
y
∑
=
=
N
k
e
kx
Cx
FMa
1
)(
,
∑
=
=
N
k
e
ky
Cy
FMa
1
)(
(14.40)
где
M
– масса тела,
Cx
a
и
Cy
a – проекции ус-
корения центра масс тела на соответствующие
оси.
Согласно теореме об изменении кинетиче-
ского момента относительно подвижного цен-
тра масс (14.39) в проекции на подвижную ось
zC
′
()
)(
1
e
k
N
k
zC
r
zC
FM
dt
dK
∑
=
′
′
= . (14.41)
Учтём, что
СCx
xa
&&
=
,
СCy
ya
&&
= ,
ϕ
&
zC
r
zC
JK
′′
=
. Тогда уравнения (14.40) и (14.41)
можно переписать в виде следующей системы уравнений
Рис. 14.11
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
39
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=
=
=
∑
∑
∑
=
′
′
=
=
,
,
,
)(
1
1
)(
1
)(
e
k
N
k
zC
zC
N
k
e
ky
C
N
k
e
kx
C
FMJ
FyM
FxM
ϕ
&&
&&
&&
(14.42)
которые представляют собой дифференциальные уравнения плоского движения
твёрдого тела.
Не обязательно для определения положения центра масс тела использовать де-
картовы координаты
C
x ,
C
y . Можно теорему о движении центра масс (14.3) спрое-
цировать, например, на оси естественной системы координат. Тогда, первые два
уравнения из системы (14.42) будут иметь вид
∑
=
=
N
k
e
k
C
FsM
1
)(
τ
&&
,
∑
=
=
N
k
e
kn
С
F
s
M
1
)(
2
)(
ρ
&
, где
C
s – дуговая координата центра масс тела.
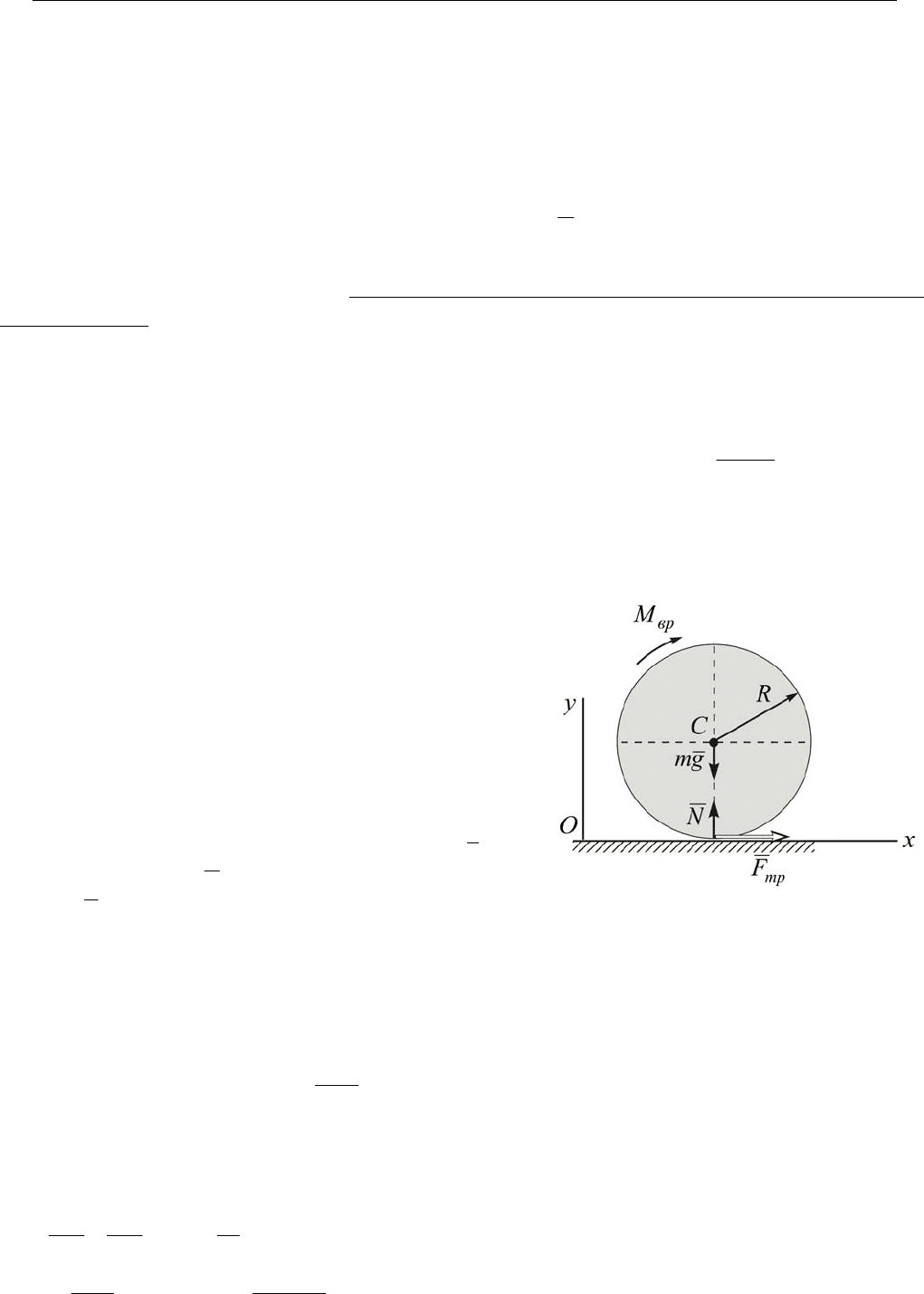
Пример. Ведущее колесо автомашины начинает движение из состояния покоя с пробуксовкой
под действием вращающего момента Нм 50
=
вр
M .
Коэффициент трения скольжения между колесом и
дорогой
5,0=f
. Масса колеса кг 20=m , его ради-
ус
м 2,0=R
.
Найти уравнения движения колеса, приняв его
за однородный диск и пренебрегая трением каче-
ния.
Решение. Колесо совершает плоское движе-
ние. Покажем его в произвольном положении (рис.
14.12) и обозначим действующие на него внешние
силы и моменты внешних сил: сила тяжести
g
m ,
нормальная реакция
N опорной поверхности, сила
трения
тр
F и момент
вр
М . Дифференциальные
уравнения (14.42) для данной задачи имеют вид
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
+−=−
−=
=
)(.)(
2
)(,0
)(,
2
вRFM
mR
бmgN
аFxm
трвр
трC
ϕ
&&
&&
Из уравнения (б) следует H 2,19681,920
=
⋅
=
= mgN .
По условию задачи колесо катится с проскальзыванием. В этом случае сила трения достигает
своего максимально возможного значения H 1,982,1965,0
=
⋅
=
=
fNF
тр
и из уравнения (а) следует
2
с
м
905,4
20
1,98
===
m
F
x
тр
C
&&
, а из уравнения (в) следует
()
()
2-
22
c 95,752,01,9850
2,020
22
=⋅−
⋅
=−= RFM
mR
трвр
ϕ
&&
.
Рис. 14.12
В.Н. Винокуров. Конспект лекций 2 по теоретической механике для машиностроительных специальностей
40
Перейдя от постоянных ускорений к координатам, имеем
00
2
2
905,4
CxC
xt
t
x ++=
υ
,
00
2
2
95,75
ϕωϕ
++= t
t
. Здесь 0
00
=
=
ω
υ
x
по условию задачи (движение начинается из состояния
покоя). Пользуясь произвольностью выбора начала отсчёта координат, принимаем 0
00
=
=
ϕ
C
x .
Окончательно, уравнения движения колеса имеют вид
м 45,2
2
tx
C
= , м 2,0
=
=
Ry
C
, рад 96,37
2
t=
ϕ
.
Теорема об изменении кинетической энергии
14.18. Кинетическая энергия точки и системы. Теорема Кёнига. Кинетиче-
скую энергию материальной точки массой m , движущейся с абсолютной скоростью
υ
, определяют по формуле
2
/
2
υ
m
T
=
.
Кинетическая энергия механической системы равна сумме кинетических энергий
точек этой системы:
∑
=
=
N
k
kk
m
T
1
2
2
υ
. (14.43)
Кинетическая энергия – положительная скалярная величина. Единицей измере-
ния кинетической энергии в системе СИ является джоуль (Дж).
Как может вычисляться кинетическая энергия системы при сложном её движе-
нии? Для ответа на данный вопрос дополнительно к неподвижной системе отсчёта
Oxy
z
(рис. 14.13) введём в рассмотрение ещё подвижную систему отсчёта zyxC
′
′
′
с
началом в центре масс – точке
C
, движу-
щуюся поступательно с центром масс (кёни-
гову систему отсчёта). Абсолютное движе-
ние системы при этом можно рассматривать
как совокупность переносного (вместе с цен-
тром масс) и относительного (по отношению
к центру масс) движений системы.
Для любого момента времени положение
произвольной точки
k
M
системы по отно-
шению к неподвижному центру O определя-
ет радиус-вектор
kck
rr
ρ
+
=
,
где
k
ρ
- радиус-вектор точки
k
A по отношению к центру масс
C
. Продифференци-
ровав это равенство по времени, найдём абсолютную скорость точки системы
r
kCk
υυυ
+= ,
где
dtd
k
r
k
/
ρυ
= - относительная скорость точки (см. вывод (14.35)).
Учитывая, что квадрат вектора равен квадрату его модуля, преобразуем выраже-
ние кинетической энергии системы к виду
Рис. 14.13
