Vilasi G. Hamiltonian Dynamics
Подождите немного. Документ загружается.


394
Integrability
of
Fermionic
Dynamics
16.3
Poisson
Supermanifold
We briefly describe how to introduce super Poisson structures
on
an
(m,
n)-
dimensional supermanifold
S.59'33
For additional results, see also
RRf.
68.
As
before, we shall denote
by
zi
=
(&,dk),
i
E
(1,.
.
.
,m
+
n}
the local coordi-
nates on
S.
By
direct calculations it can be proven' that
If
(wij)
is an
(m
+
n)
x
(m
+
n)
matrix, depending upon the point
z
E
S,
with the follouing properties:
the elements
wij
are homogeneous with parity
p(d)
=
p(zi)
+p(zj)
+
p(w)
and
p(w)
not depending
on
the indices
i
and
j;
0
=
-(_l)lP("i)+P(w)llP("j)+P(w)lWij
,
(16.10)
then, the follouing bracket
e
-+
d
a
aza
dzi
(F,G}
=:
F
-
wii
-
G
(16.12)
makes
G(S)
a Lie superalgebra (Poisson superstructure).
We have two different kind
of
structures according to the fact that
p(w)
=
0
(even Poisson structure),
or
p(w)
=
1
(odd Poisson structure). Indeed, one can
check that the bracket
(16.12)
has properties:

Poisson
Supermanifold
395
We infer from Eqs.
(16.13)
and
(16.14)
that, when thought of
as
elements of
the Poisson superalgebra, homogeneous elements
of
Q(S)
preserve their parity
if
p(w)
=
0,
while they change it if
p(w)
=
1.
If
the
matrix
(wid)
is regular, then its inverse
(wij),w,jwjk
=
6tl
gives the
components of
a
symplectic structure
w
=
idzi
A
dzJwji,
namely,
w
is closed
and nondegenerate with the properties
P(Wij)
=
P(4
+
P(4
+
P(W)
1
(16.15)
and
w
is
homogeneous with parity just equal to
p(w).
Theorem
41
w
homogeneous. Then,
Proposition
42
There
is
also a
Darboux the0~em.l~~
Let
(S,
w)
be
an
(m,
n)-dimensional symplectic manifold with
0
Ifp(w)
=
0,
then
dim
S
=
(2r,
n)
and there exist local coordinates such
that
1,
0
w
=
dqi
A
dpi
+
d('
Ad<'
Wij
=
(-:,
:)
.
(16.16)
0
Ifp(w)
=
1,
then
dim
S
=
(m,m)
and there exist local coordinates
such that
w
=duiAdc,
wij
=
(
':)
.
-1,
By
having a Poisson structure, we can deal with Hamilton equations. From
Eq.
(16.12),
if
H
is the Hamiltonian, the corresponding equations are
(16.17)
Now
we would like to maintain the possibility
of
explicitly constructing
the flow of Eq.
(16.17).
This requires that the dynamical evolution be an
even vector field. In turn this implies that the Poisson structure and the
Hamiltonian function should have the same parity
so
that in particular, with
an odd Poisson structure, we need an odd Hamiltonian function.
Before we analyze the graded Nijenhuis condition, we will study a few
examples.

396
Integrability
of
Fermionic Dynamics
Example
43
(Bosonic -Fermionic oscillator)
The mized bosonic-fermionic
harmonic oscillator
in
(2,2)
dimensions is described with coordinates
(q,p,
q,
()
and has the following equations
of
motion:
(16.18)
Equations
(16.18)
can be given two Hamiltonian descriptions, The Hamiltoni-
ans are the usual even one
H=
;@2+42)+i<q,
(16.19)
and an odd one
K
=
PE
-k
477
7
while the two Poisson structures
am
respectively
(16.20)
0100
AH=(-;
:
a
I)
i
oooi
and
We
can construct
a
mixed invariant tensor field
T
by
0010
0
0
01
0400
i
0
00
T
=:
WH
o
AK
=
(16.23)

Powson
Supermanafold
397
However, this odd tensor field (p(T)
=
1)
is
not a recursion operator. Indeed,
it
is
easy to check that
so
that
TdK
=
dH
,
d(TdH)
#
0.
(16.24)
If
we evaluate the Poisson brackets
of
the coordinate variables, by using the
two symplectic structure given by
Eqs.
(16.21)
and
(16.22),
we
find
that
{q,p)H
=
1
>
{P,q}H
=
-1
9
{V,q}H
=
i
{<,<}H
=
i
7
(16.25)
and
{Q,<}K
=
1,
{<,Q}K
=
-1
9
{P,V)K
=
-1
>
{7),P}K
=
1
>
(16.26)
the remaining ones being identically zero. We see that the sum
{.,
.}+
of
the
two structures
is
itself a Poisson structure with the property
{F,
G}+
=
-(-l)P(F)J’(G)
{G,
F}+
>
(16.27)
but
it
has not definite parity. Moreover the bracket
(0,
.}+
is
degenerate.
Example
44
(Witten
dynamics)
Interesting examples come from super-
symmetric dynamics.
It
has been that the dynamics
of
Witten’s
Hamilton systems184 can be given a bi-Hamiltonian description with an even
Poisson bracket and Grassmann even Hamiltonian,
or
with an odd bracket and
Grassmann odd Hamiltonians. Instead
of
considering the general case we
shall
study a supersymmetric Toda chain with coordinates
(q,
p,
q,
<).
The even Hamiltonian
is
given by
(16.28)
1
H
=
z(p2
+
eq)
+
Ji57/e$
.
2
With
the even Poisson structure
398
Integrability
of
Fermaonic
Dynamics
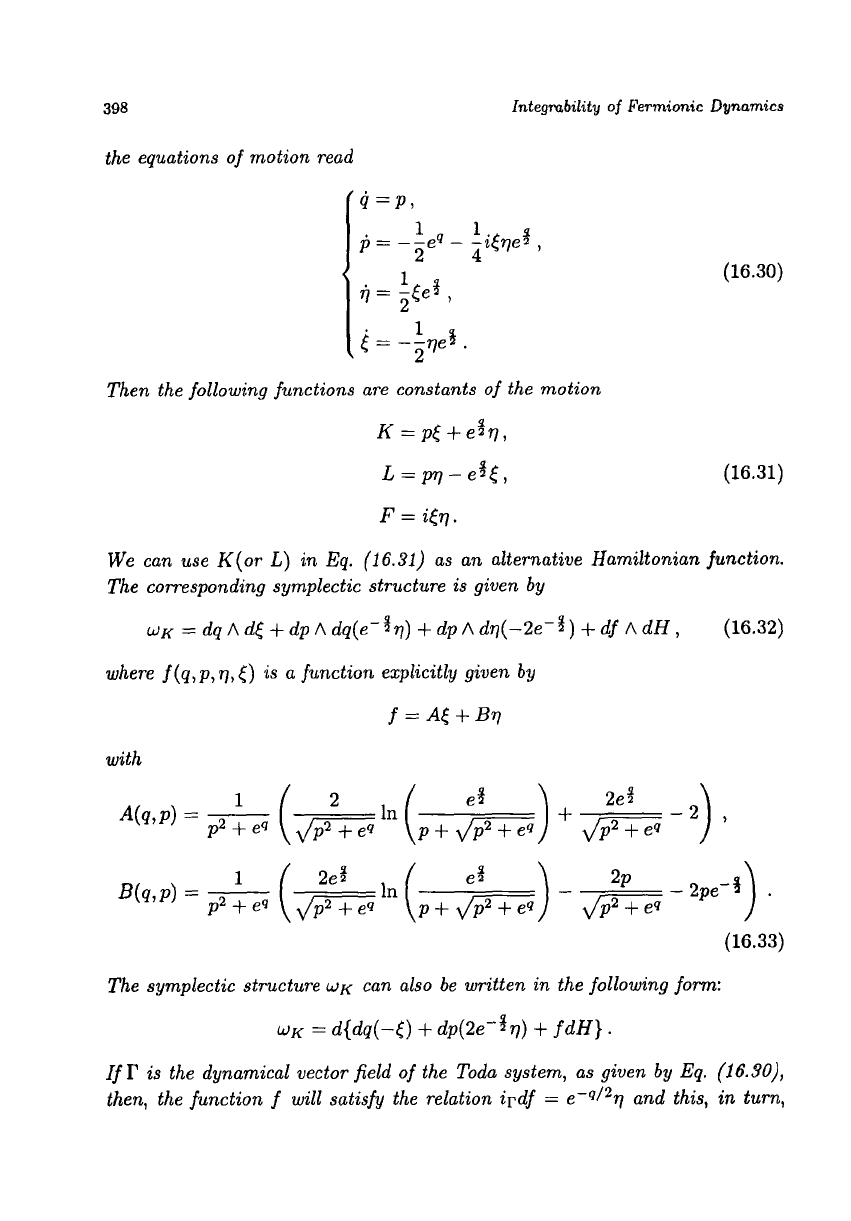
the equations of motion read
(16.30)
Then the following functions are constants of the motion
(16.31)
We can use K(or
L)
in
Eq.
(16.31)
as an alternative Hamiltonian function.
The corresponding symplectic structure is given
by
WK
=
dq
A
d<
+
dp
A
dq(e-4q)
+
dp
A
dq(-2e-4)
+
df
A
dH,
(16.32)
where
f(q,p,q,[)
is a function explicitly given by
f
=
A[
+
Bq
with
(16.33)
The symplectic structure
WK
can also be written
in
the following form:
WK
=
d{dq(-t)
+
dp(2e-$7)
+
fdH}
.
If
r
is the dynamical vector field of the Toda system,
as
given by Eq.
(16.30),
then, the function
f
will satisfy the relation irdf
=
e-qI2q and this,
in
turn,

Poisson
Supemanajold
399
ensures
that
+WK
=
dK.
It
take some algebra
to
check that the
(1,
1)-tensor
field
T
=
WX
0
AH,
(16.34)
is
such
that
TdH
=
dK,
d(T2dH)
f:
0.
Again, the tensor
field
T
in
Eq.
(16.34)
is
not
a
recursion operator
(16.35)
16.3.1
Super
N'jenhuis
torsion
Let
us
recall that one
of
the most relevant consequences deriving from
a
(not
graded) (1
-
1)-tensor field
T,
with
a
vanishing Nijenhuis torsion,
is
the
pos-
sibility to generate sequences of exact differential l-forms according to
NT
=
0,
d(TdF)
=
0
===+
d(TkddF)
=
0.
(16.36)
The above relation is
a
consequence
of
the identity
X
AY
I
d(T2a)
=
{X
ATY
+
TXAY}
I
d(Ta)
-
{TXA
TY}
I
da
-
3CT(X,
Y)
I
a:
*
(16.37)
in which
a
is
any differential l-form.
Indeed, by assuming that both
a
and
Ta:
are closed,
Eq.
(16.37) implies
that
T2a
is
closed
if
and only if
311.
=
0,
namely
if
and only if the
Nijenhuis
torsion
of
T
vanishes.
Let
us
analyze now the graded situation. Suppose
T
is
a
graded
(1,l)-
tensor field that
is
homogeneous
of
parity
~(7').
Then,
if
a
is
any differential
l-form, by using the definition Eq. (16.5), after some (graded) algebra, the
analogue
of
Eq.
(16.37) reads
x
A
y
1_
d(T2a)
=
{(-l)p(T)p(Y)X
A
TY
+
(-l)p(T)[p(X)+p(Y)lTX
A
y}
I
d(Ta)
-
(-1)
P(T)[P(X)+P(T)lTX
A
TY
I
da
-
(-l)p(T)G3C~(x,
Y)
i
Q
+
(-l~p(~)p(x)~l
-
(-l)p(T)]~~x~TY
I
a),
(16.38)
where
G7.1~
is
defined in Eq. (16.9).

400
Integrability
of
Fermionic Dynamics
It is clear then,
that
for
a
(1,
1)
odd tensor field a
(1,
P)-tensor field
corresponding to its super Nijenhuis torsion can be defined only whenp(T)
=
0.
The same result is attained with the use of the general approach
dT
o
dT
=
0.
Summing up, we have shown that there are examples of dynamical systems
whose dynamical vector field
I?
admits two Hamiltonian descriptions, odd and
even, respectively, and that the tensor field
T,
constructed out
of
the corre-
sponding Poisson structures is not
a
recursion operator since it cannot generate
new integrals of motion after the first two ones.
We have also shown that this fact is general and that for
a
generic-graded
(1, 1)-tensor field
T,
a
graded Nijenhuis torsion cannot be defined
unless
T
is
even.
F’rom the nature of the proof it seems plausible that
a
similar theorem
should hold true also
in
infinite dimensions.
The
no
go
theorem we have proved in
our
paper does not exhausts, obvi-
ously, the analysis of complete integrability for graded Hamiltonian systems.
Much more attention must be paid, however, in generalizing to the graded case
geometrical structures that play a relevant and natural role in the nongraded
situation.
Further
Readings
0
M.
Batchelor, “Graded
Manifols
and Supermanifolds,”
in
Mathematical Aspects
of
Superspace,
Clarke, C.
J.
S.,
Rosenblum,
A.,
Seifert,
H.-J.
eds. (Dordrecht,
Reidel,
1984).
0
M.
DuboisViolette, “DQrivation et calcul differbntiel non commutatif,”
C.
R.
Acad.
Sci.
Paris
307
SJrie
I403
(Paris,
1988).
0
B.
A.
Dubrovin,
Geometry
of
Hamiltonian
Ewolvtionary
System
(Bibliopolis,
Naples,
1991).
0
Faddeev and V.
E.
Korepin,
L‘Quantum Theory
of
Solitons,”
Physics
Reports
42C,
1 (1978).
0
S.
P.
Novikov,
S.
V. Manakov,
L.
P.
Pitaevskii,
and
V.
E.
Zakharov,
Theory
of
Solitons:
The
Inverse Scattering Method
(Consultants Bureau,
New
York,
1984).

Appendix
A
Lagrange:
A
Short
Biography
Lagrange
is
considered one
of
the greatest mathematicians
of
the modern age
and it
is
jmpossibIe, in
a
few pages, to quote his enormous contribution
to
mathe~atics and physics. Thus, we shajl limit ourselves to
a
short biogr~phi~
note.
Giuseppe Luigi Lagrangia was born in Torino on January
25,
1736,
and
died in
Paris
on
April
10,
1813.
At
the age of
19
he aIready
ww
Professor of
Mathematics
at
Artillery’s School in Torino and soon after associate founder
of the Ac~~my
of
Sciences
of
Torino. The
first
fruit of Lagrange’s works here
wits
his
letter, wrjtten when he
was
still only
19,
to Euler, in which he solved
the isoperimetrical problem, which for more than half
a
century, had been
;t
subject
of
discussion.
“To
effect the solution he enunciated the principles of the
calculua
of
variations. Euler recognized the generality
of
the method adopted,
and its superiority to that used by himse~~ and with rare courtesy he withheld
a
paper he had previously written, which covered some
of
the same ground,
in
order that the young Italian might have time to complete his work,
and
claimed the undisputed invention
of
the new calculus”.46
Most
of
Lagrange’s early writings are to be found in the five voIumes of
sacti ti#^
of
Turin Academy, usually known
as
the
~~sce~lu~eu
~a~r~nens~~.
The first volume contains
a
memoir
on
the theory of sound propag~tion.
In
this
he
indicates
a
mistake made by Newton, obtains the general differen-
tial equation for the motion and integrates it
for
motion in
a
straight line.
In
401

402
Lagrange:
A
Short Biography
this volume is to be found a complete solutions of the problem of
a
string
vibrating transversely. In particular, the article points out
a
lack
of
gen-
erality in the solutions previously given by Taylor, D’Alembert, and Euler;
arrives
at
the conclusion that the form
of
the curve
at
any time
t
is given by
y
=
asinmxsinnt, and concludes with
a
masterly discussion of
echoes, beats,
and
compound sounds.
In this volume, other articles concern
recurring series,
probabilities,
and
calculus
of
variations.
The second volume includes remarks on the theory and notation
of
the
calculus of variations, already discussed in the first volume, the derivation of
Least Action Principle
as
an illustration
of
the method, and solutions of various
dynamical problems.
The third volume, besides the solutions of additional dynamical problems
by means of the calculus
of
variations, and some articles on the integral cal-
culus, includes the general differential equations of motion for three bodies
moving under their mutual attractions.
In a word, in 1761 Lagrange stood without
a
rival
as
the foremost mathe-
matician living. In his paper in 1764, on the libration of the moon, he explains,
with the aid of the
Principle
of
the Virtual Work,
why the moon always turns
to the earth the same face. Here there was already, in germ, the future gener-
alized equations of the motion.
“In 1766 Euler left Berlin, and Frederick the Great immediately wrote
expressing the wish that ‘the greatest King in Europe’ to have ‘the greatest
mathematician in Europe’ resident at his court. Lagrange accepted the offer
and spent the next twenty years in Prussia, where he produces, not only the
long series of memoirs published in the Berlin and Torino transactions, but his
monumental work, the
Me‘canique Analytique”
.46
Indeed, during these
20
years, Lagrange contributed one memoir per month,
on the average, to the Academies of Berlin, Torino, and Paris. All his memoirs
are of high scientific level. Moreover, some
of
them are actually treatises.
Among the ones sent to Paris it is worth to mention the memoir on the Jovian
system (1766), the essay on the three body problem.(1772), the article on the
secular equation of the moon (1773), and the treatise on cometary perturbation
(1778).
For all these memoirs, the
Acadkmie the fiance,
who had proposed
the subjects, awarded a prize to Lagrange.
In 1787, after the death of Frederick, Lagrange “who had found the cli-
mate of Berlin trying, gladly accepted the offer of Louis XVI to migrate to
Paris. He received similar invitations from Spain and Naples”.46 The decree

Lagrange:
A
Short
Biography
403
of October
1793,
which ordered all foreigners to leave F’rance, specially ex-
empted
him
by name. He was offered the presidency
of
the commission for the
reform
of
weights and measures and the different revolutionary governments
loaded
him with honors and distinctions. In
1795,
Lagrange was appointed to a
mathematical chair at the newly-established
dcole
~o~ule,
which enjoyed
only
a
brief existence
of
four months, and in
1797,
he was made professor at
the
l$cole Polytechnique.
In appearance Lagrange was
of
medium height, and slightly formed, with
pale blue eyes and a colorless complexion. In character, he was nervous and
timid, he detested controversy, and to avoid it willingly allowed others to take
the credit
for
what he had himself done. Indeed, no inconsiderable part of the
discoveries of his great contemporary, Laplace, consists
of
the application of
the Lagrangian formulae to the facts of nature. Even the introduction
of
the
mornentu
and of the
Po~sso~
bracket
occur in the writings of Lagrange
as
well
as
the theory
of
~d~ct~~~
of
the ~rob~e~
of
n
bodzes.
