Vilasi G. Hamiltonian Dynamics
Подождите немного. Документ загружается.


A
of tensor fields sat~sfying Eq.
(15.2)
is
generally
a
different zero. This is, for
instance, the case for the tensor field given by Eq.
(15.5).
15.1.3
We recall that the evolution equation
is
The
A-invariant tensor
field
for
KdV
ti+uux+uxox
=o,
and that
a
tensor field satisfying the equation
CAT
=
0
(15.3)
is
given
by
the operator field
T*
=
a,,
4-3u.f
-
ux
/x
-dy,
whose adjoint is used for construction of the sequences
of
conserved function-
als and
is
related by a Miura-like transformation,
of
tensorial nature, to the
analogous operator for the sineGordon equation. Equation
(15.7),
explicitly
written acquires the form
?’
=
[A,
T]
with
A
=
a,,,
-
ua,
-
u,.
Remark
24
~~~a~~cs,
q-equzualent ~ag~angiu~~~*~
al~a~s
lead
to
a
A-invar~a~t
T.
3
--oo
The
ezistence
of
~-inva~ant
T
is
so
pecu~aa~ in ~agru~gian
15.1.4
In order
to
consider the usual
L
for KdV we will again adopt the coordinate
notation in terms
of
“local
coordinates”
u(z):
differentials
du(z)
and functional
derivatives
d/(su(z)),
as
formal elements
of
the “continuous natural bmis” of
cotangent and tangent spaces, respectively. The vector field is then written as
The
A-covariant tensor
field
for
KdV
s
M
A
=
1,
dzA(u)-
6u(x)
’
It
is
easy to verify that the Lie derivative of the Lax tensor field,
corresponding to the
Lax
operator
I,
=
ax,
+
(1/6)u,
does not vanish.

A
Tensoda1 Version
of
the
Lax
Representation
375
If,
on the other hand, we consider the connection form
m
with
we
obtain
1
ker(B)
=
-i~w[z,
31
=
4d'"(x
-
y)
+
~(o)d'(~
-
y)
-
pxS(s
-
y)
,
and hence
1
2
B
=
4axsx
-
ua,
-
-24%
*
Therefore, the
Lax
representation for KdV equation can be written in the
form
DAL
=
0.
In order to illustrate the utility of the geometrical reading of the LR
as
a
condition of parallel transport, consider the transformations of the Lax pair
induced
by
transformations
of
field variables.
This
matter
is
relevant accord-
ing to the general
f~ling138~17g~180~105~11g
that several integrab~e nonlinear field
theories
are
equivalent between them, up to inversion problems of transforma-
tions. This point of view has, for instance, led to connect the
T
operators
for
sineGordon and KdV and the
T
operators for Liouville' equation and KdV.
To
give
a
simple example of the tr~sformation method, consider once again
the harmonic oscillator.
To
transform, for instance, the Lax pair
to action-angle variables
(J,
cp),
L
must be transformed as (l,l)-tensor field and
B
as
the contraction
of
the co~~ction form
(15.4)
with the dynamical vector
field.
The
transformation law for
w
from the natural basis in
x
coordinates to
that in
o'
is
Wf
=
(~)
w
(~)
f
(~)
d
(g)
.

376
Miscellanea
Then, in the new frame
-mcoscp -2sincp
)
,
(
o
$)
-msincp
&i7coscp
-J
L=
(
B=
,
which are, of course, a
Lax
pair for the dynamics
J
=
0,
@
=
1.
15.2
Liouville Integrability
of
Schrodinger
Equation
Some years ago it was suggested176 the use of complex canonical coordinates
in the formulation of
a
generalized dynamics including classical and quantum
mechanics
as
special cases. In the same spirit, a somehow dual viewpoint
can be proposed151: rather than to complexify classical mechanics
it
may be
useful to give a formulatioli of quantum mechanics in terms of
realified
vector
spaces.
By using the Stone-von Neumann theorem, a quantum mechanical system
is associated with
a
vector field on some Hilbert space
(Schrodinger picture)
or
a vector field; i.e. a derivation, on the algebra of observables
(Heisenberg
picture).
In classical mechanics the analog infinitesimal generator of canonical trans-
formations is a vector field on a symplectic manifold (the
phase space).
Therefore, if we want to use similar procedures, we need to real-off &(Q,
C),
the Hilbert space of square integrable complex functions defined on the con-
figuration space
Q,
as
a symplectic manifold
or,
more specifically,
its
a co-
tangent bundle. We shall see that it can be considered
as
T*(Lz(Q,IR));
&(Q,
9)
denoting the Hilbert space of square integrable real functions defined
on
Q.
The approach is different from previous ones124@*71169 also dealing with the
integrability of quantum mechanical system in the Heisenberg and Schrodinger
picture.
In order to make more transparent the geometrical and the physical con-
tent of the subject, difficult technical aspects (which are however important in
the context of infinite dimensional manifold,"
as
for instance, the distinction
between
weakly
and
strongly
not degenerate bilinear forms,
or
the inverse of
a Schrodinger operator and
so
on) will not be addressed. We shall limit
our-
selves to again observe that no serious difficulties arise working on an infinite
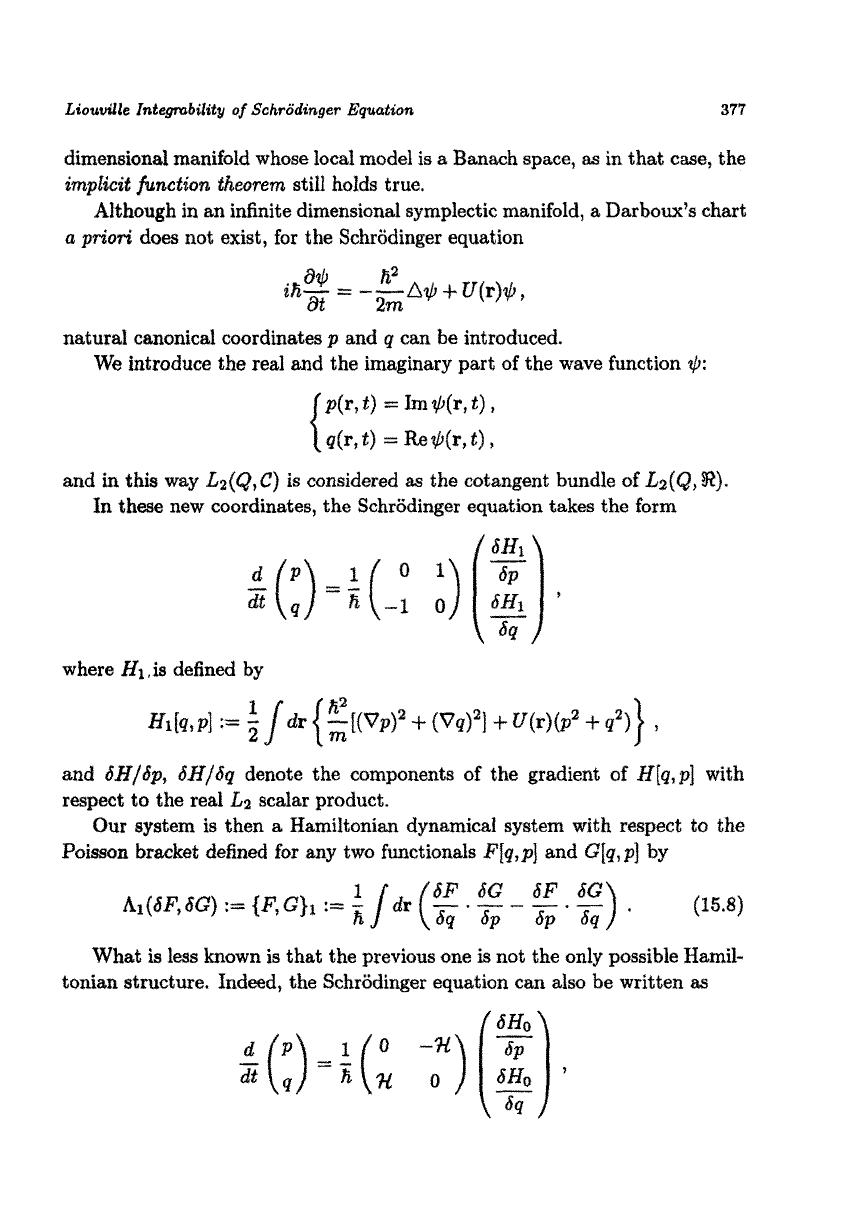
Liouville
Integmbility
of
Schrodinger
Equation
377
dimensional manifold whose local model
is
a
Banach space,
as
in that case, the
implicit
function
theorem
stil holds true.
Although in an infinite dimensional symplectic manifold,
a
Darboux’s chart
a
priori
does not exist, for the Schrodinger equation
natural canonical coordinates
p
and
q
can be introduced.
We
introduce the real and the imaginary part of the wave function
20:
p(r,
$1
=
Im
“1
t>
1
i
a@,
t)
=
~+(r,
t>
>
and
in
this
way
L2(Q1C)
is
considered
as
the cota~ent bundle
of
I&(&,
sz).
In these new coordinates, the Schrodinger equation
takes
the form
where
HI,
is
defined by
and
GH/Gp,
G~/~q
denote th0 components
of
the gradient
of
H[q,p]
with
respect
to
the real
1;2
scalar product.
Our
system is then
a
Ham~ltoni~ dyn~ical system with respect to the
Poisson
bracket defined for any two functionals
F[g,p]
and
G[q,p]
by
What
is
less known
is
that the previous one
is
not the only possible Hamil-
tonian structure. Indeed, the ~chro~nger equation can also be written
as

378
where
HO
is defined
by
and
31
is
the
Schrodinger operator
It
is then again a Hamiltonian dynamical systems with respect to
a
new
Poisson bracket which, for any two functionals
F[q,
p]
and
G[ql
p],
is
defined
bY
Thus, with the same vector field, we have the two following choices:
A
phase manifold with a universal symplectic structure
w1
:=
12
dr(6p
A
6q)
S
s
and a Hamiltonian funct~onal d~pending on the classical potential,
o
A
phase manifold
with
a
symplectic structure determined by the
clas-
sical potential
wg
:=
ti
dr(%-’Sp
A
Sq)
and the universal ~amiltonian func~~ona~ representing the quantum
probability.
The two brackets satisfy the Jacobi ~dentity,
as
the associated differentia1
2-forms are closed for they do not depend on the point
+
zz
(p,
q)
of the
phase
spuce.
We have then the relation
where
(15.9)

LiouviEle Integmbilzty
of
Schrodinger
Equation
and
379
6H
6H
-=[$
621
Since the tensor field
T
does not depend on the point
$J
3
(p, q)
of the
phase
space,
its torsion is identically zero,
so
that the relation
(15.9)
can be iterated
to
-=p-.
6Hn
6HO
6U
621
It
turns out that the Schrodinger equation admits infinitely many conserved
functionals defined by
They are all in involution with respect to the previous Poisson brackets:
It is worth stressing that for smooth potentials
U(z)
in one space dimension,
the eigenvalues of the Schrodinger operator
Ifl
are not degenerate,
so
that the
eigenvalues of
T
are double degenerate.
The eikonal transformation
The map
p(r,
t)
=
A(r,
t)
sin
-
S(r,
6'
is a canonical transformation between the
(p,
q)
and
(T
=
S(2h)-'&,
x
=
A2)
coordinates, since

380
The Hamiltonian
HI
becomes
Miscellanea
so
that Hamilton’s equations
give
div(XV.rr)
,
ax
2ii
-
=
--
at
2m
where
P
=
x
and
J
=
hx(VS/m) represent the
probability density
and the
current density,
respectively.
This transformation being nonlinear will transform previous bi-Hamiltonian
descriptions into
a
mutually compatible pair of nonlinear type.
Finally, it is worth to stress that the Schrodinger equation, in spite of its
linearity, shows that the class of completely integrable field theories in higher
dimensional spaces
is
not empty. Moreover, previous analysis appears to be
interesting also in the formulation of variational principleslog for stochastic
mechanics.
15.2.1
The two-dimensional nonlinear Schrodinger equation
Comparison with the nonlinear Schrodinger equation
(1
5.10)
has been analyzed by several authors.
lS6*
lZ2*
lS8tg5

Liouville
Integmbildty
of
Schrodinger
Equation
381
it takes the form
~KI
z(:)=;(:
dt
-:)
(z)
-
69
'
where
K1
is
defined by
1
ti2
h'lkl,
PI
:=
5
J
t.&E
{
-GI(a3P)2
4-
+
(P2
+
212)
-
It
is
then a Hamiftonian dynamicai system with respect to the canonical
Poisson
bracket
A1
defined by
Eq.
(15.8):
The previous one
is
not the only possible Hamiltonian structure.
As
matter
of
fact the nonlinear Schrodinger equation can
also
be written
ad22*138
where
%!N
is the
Poisson
operator
or
equivalently,

382
Mdscel
tanea
with
Q:
=
~~m/~,
and
It is then again
a
Hamiltonian dynamical systems with respect to
a
new
Poisson bracket+ given, for any
two
functionals
F[q,p]
and
G[q,p],
by
Once again, with the same
vector
field,
we have two following
choices:
*
A
phase manifold with the canonical symplectic structure
and a Hamiltonian functional accounting
for
the interaction.
teraction
*
A
phase manifold with
a
symplectic structure determined
by
the in-
~2
3
AT1
:=
ti
dx(~~'6~
A
Sy)
s
and
a
free
HaIniltonian functional given by the mean value
of
the
momentum
?j
=
-iMS.
We
have then the relation
where
(15.11)
I
-2cYpL)-'q
It
can be shown that the sum
A2
-t
A1
is
again
a
Poisson bracket.
This
is
equivalent to the vanishing of the torsion of the tensor field
TN,
so
that the
tFor
simplicity the
proof
of
Jacobi
identity
for
A2
is
omitted.

Liouville Integrability
of
Schrodinger Equation
383
relation (15.11) can be iterated to
(15.12)
Therefore, the nonlinear Schrodinger equation admits infinitely many con-
served functionals. The first three hnctionals are
They are all in involution with respect
to
the previous Poisson brackets, i.e.
By observing that
the recursion relation (15.12) can be completed to
In terms
of
the operators
T,
TG, TK,
TN
defined by
we have the general scheme on the next page.
