Викулин А.В. Физика Земли и геодинамика

Подождите немного. Документ загружается.

должна заключаться в определен и физической поверхности Земли, и внешнего

гравитационного поля. М.С. Молоденский высказал мысль о том, что триангуляцию

нужно редуцировать сразу на эллипсоид, минуя сложн й и неизвестный геоид. Геоид в

этом случае не определяется, но его и не нужно определять. Задача геодезии состоит в

определении земной поверх

ности и

внешнего гравитационного поля. Эту задачу геодезия

ожет

с е

е .

рушинский, 1976, с. 329].

Вопрос о фигуре Земли имеет принципиальное значение. «Если для планеты

за ь

ускорение планеты»

тенберг, 1963, с. 26].

, ,

ид) и отмечается, что

6-224] в качестве причин, влияющих на изменение фигуры Земли,

отмечаются ротационные и космические факторы, а также блоковое строение планеты. Во

второй части книги мы коснемся вопроса, как эти факторы могут учитываться в рамках

вихревой геодинамики.

м и должна решать на основании лишь проведенных измерений, без привлечения

каких-либо гипотез о внутреннем тро нии Земли. В теории М.С. Молоденского за

фигуру сравнения (относимости), относительно которой определяется фигура реальной

Земли, принимается уровенный эллипсоид, потенциал которого находится в результате

решения з дачи Стокса –

квазиг оид

Квазигеоид на поверхности океана совпадает с геоидом. На материках квазигеоид

будет тем больше отступать от геоида, чем больше аномалии силы тяжести и чем сложнее

рельеф местности. На материках квазигеоид может быть принят за приближенное

выражение для геоида [Г

С этой новой современной точки зрения проблема редуцирования измеренных

величин

на геоид потеряла для геодезии свое значение [Бровар, Магницкий, Шимьерев,

1961, с. 58; Бровар, Юркина, 2001].

М.С. Молоденский - автор первой отечественной «Инструкции по

гравиметрическим работам ля общей основной гравиметрической (маятниковой) съемки

СССР» (1935) и автор первого отечественного гравиметра ГМК – гравиметр кольцевой

Молоденского [Геодезия, 2008а, с. 461].

1960 г. - выход в свет основополагающего руководства М.С. Молоденского, В.Ф.

Еромеева и М.П. Юркиной [1960] «Методы изучения внешнего гравитационного поля и

фигуры Земли», на основе которого развивается овременная геодезия [Бровар, Юркина,

2001].

1963 г. - выход в свет первого издания фундаментального труда Н.П. Грушинского

(1915-2001) «Теория фигуры Земли», в котором автор развил современную концепцию

физической геодезии [Ге дезия, 2008а, с. 189-190; Грушинский, 1976].

О фигуре реальной Земли

даны ее фигура, распределение масс и параметры движения, то можно определит

силы тяжести на любой эквипотенциальной поверхности этой

[Гу

Традиционно для Физики Земли и Геофизики проблема фигуры Земли

рассматривалась в рамках описанного выше ньютоновского подхода

с ориентацией на

получаемые экспериментальные данные [Жарков, Трубицын, Самсоненко, 1971;

Магницкий, 1965, 2006; Орленок, 2000; Стейси, 1971; Теркот Шуберт 1985; Трухин,

Показеев, Куницын, 2005].

Но есть и друг е работы. Так, в работе [Гутенберг, 1963, с. 23-25] реальная фигура

поверхности Земли сравнивается со всевозможными приближенными достаточно

гладкими фигурами (шар, эллипсоид вращения, трехосный эллипсо

эквипотенциальные поверхности в виде

геоидов, близких к среднему уровню моря, имеют

наиболее малые отклонения от истинной поверхности Земли. В работе [Хаин,

Короновский, 2007, с. 21

Сложность и противоречивость проблемы отмечал и патриарх советской геодезии

и геофизики М.С. Молоденский [2001, с. 96]: «Ни один из вопросов теоретической и

прикладной гравиметрии не привлекал к себе такого внимания, как вопрос о редукции

силы т

ено значительное число методов редуцирования,

кажды

чиная с

сообра

ой точностью определения гравиметрических

пункто

дальне

–

понимать форму физической поверхности твердой

части п

учен

.1).

яжести к уровню моря. Этому вопросу посвящены сотни работ, трактующих его с

различных точек рения. К способу редуцирования силы тяжести геодезисты, геологи и

геофизики предъявляют различные требования, вытекающие из особенностей решаемых

ими задач. В связи с этим предлож

й из которых обладает известными преимуществами и

недостатками, более или

менее существенными в условиях той или иной конкретной задачи. При оценке этих

методов приходится принимать во внимание целый ряд обстоятельств, на

жений теоретического порядка и кончая чисто практическими мотивами,

связанными, например, с современн

в, их распределением, с объемом вычислительных работ и пр. Мы

не имеем

возможности осветить этот вопрос всесторонне…» (курсив – А.В.). Поэтому в

йшем при изложении материала этой главы будем иметь в виду исключительно ту

сторону проблемы, которая связана только с задачей изучения формы Земли и ее

размеров.

Понятие об истинной фигуре Земли геоиде и его геометрическое представление

[Трухин, Показеев, Куницын, 2005, с. 13-18; Стейси, 1972; с. 30-34]

Под формой Земли естественно

ланеты. Однако в силу большой сложности этой твердой поверхности из нее давно

стали выделять олее простую (более гладкую часть), в качестве которой принимают

невозмущенную приливами, ветрами и т.д. поверхность океана, продолженную

некоторым образом под континенты. Для такого приближения имеются достаточно

веские

основания, так как на долю поверхности океана приходится большая (3/4) часть

поверхности всей планеты. От этой поверхности "уровня моря" и ведется отсчет высот

при из ии формы реальной поверхности Земли или ее рельефа.

Вращение Земли создает центробежные силы которые приводят к образованию

экваториального вздутия из-за которого форма Земли существенно отличается

от

сферической (рис. 2

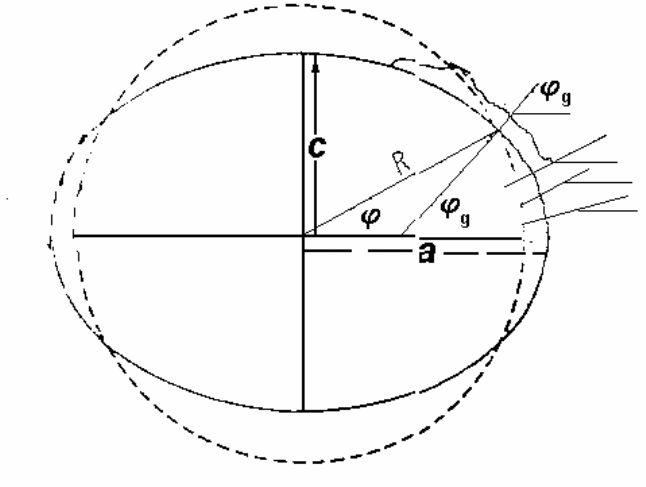
ис. 2.1. Сравнение геоида (сплошная линия) с шаром того же объема (пунктирная линия).

Сжатие геоида пре

а и с – большая

(экв

–

угол между нормалью к поверхности геоида в точ е наблюдения и экваториальной плоскостью.

увеличено примерно в 50 раз. Радиус шара R=(a

1/3

, где

аториальная) и малая (полярная) полуоси. Координата

- географическая широта точки;

Если бы весь земной шар был покрыт морем, то форма поверхности (без учета

несущественных возмущений, вызванных ветром, приливами и т.д.) полностью

определялась бы гидростатическим равновесием воды под действием силы тяжести и сил,

возникающих из-за вращения Земли.

Получающаяся соответствующая невозмущенн ню моря

эквипотенциальная поверхность - поверхность, вдоль которой гравитационный потенциал

я для жно

силы тяжести. Фигуру Земли традиционно

определяют фигурой гео ости в районах суши,

при более

строгой постановке перейти к понятию

нкте наблюдения определяется

, или направление локального вектора силы тяжести относительно звезд. По

результатам съемок, прои спутниковых

наблюдений

были определены следующие параметры геоида: экваториальный радиус а =

ус (радиус равновеликого шара)

ому уров

остается постоянным, называется

геоидом, который и определяет фигуру Земли.

Под материками поверхность геоида криволинейна, т.е. проекция его поверхности

по любому азимуту переменная кривая.

Геоид не является правильной геометрической фигурой, за поверхность геоида

принимается некая поверхность, которая перпендикулярна к линии отвеса во всех точках.

Чтобы пон ть геометрический смысл понятия геоида суши, ну представить

себе достаточно узкие каналы, прорытые через материки и соединенные с океанами.

Уровень воды в таких каналах примерно соответствовал бы поверхности геоида.

Фигура Земли – обобщенная форма поверхности Земли, обычно совпадающая с

уровенной поверхностью потенциала

ида, однако неопределенность его поверхн

задачи, за специалистовставила

квазигеоида [Геодезия, 2008б, с. 370].

Форма геоида была установлена астрономо-геодезической съемкой, проведенной

о нескольким дугам на материках. В каждом пуп

вертикаль

зведенных с 1900 по 1960 гг., и по результатам

6378245 м, полярный радиус с = 6356863 м, едний радиср

ca = 6371032 м, площадь поверхности Земли 5,1·10

км (из них на долю суши

приходится 29,2%, на долю океана 70,8%), ее объем

= 1,1·10

и средняя плотнос

км

, масса М = 6·10

г ть

= 5,5 г/см

экваториальным a и полярным c радиусами составляет малую

Разность между

величину а – с = 21,4 км,

что и определяет сжатие геоида равное [Таблицы, 1976, с. 991-

992; Трухин, Показеев, Куницын, 2005, с. 15]:

00335,0

255,298

−

. (2.1)

Как видим, поверхность реальной Земли отклоняется от сферы небольшую

еличину, примерно равн

на

ую 1/300.

На средний геоид накладываются приливные эффекты, вызванные градиентами

гравитационных полей Луны и Солнца. Но со

сжатием Земли, вызываемые ее вращением. Детали рельефа земной коры (материки,

горные хребты) создают заметное отклонение

реальной земной поверхности от геоида.

глу е (принцип изостазии) ослабляет влияние

геоида

эти эффекты очень малы по сравнению

Однако компенсация масс на некоторой бин

рельефа земной поверхности на форму .

Геофизическое обоснование геоида. Сфероид Клеро

[Магницкий, 1965, с. 200-206; 2006, с. 209-215; Трухин, Показеев, Куницын, 2005, с. 16-18]

Для определения физического смысла геоида введем в рассмотрение потенциал

силы тяжести W, который слагается из потенциалов гравитационного притяжения V и

центробежных сил U:

ϕωω

222222

cos

)(

rVyxVUVW −=+−=+=

, (2.2)

я из закона

всемирного тяготения Ньютона, согласно

оторому сила притяж

dm на расстоянии

ежду их центрами тя

где

- угловая скорость вращения Земли. Ось z направлена по оси вращения Земли, а x, y

или r,

(широта) - координаты точек на земной поверхности. В точках внутри Земли

полный потенциал содержит еще один член, зависящий от давления. На поверхности

ускорение силы тяжести, по определению направлено по нормали к геоиду. Таким

образом, задача вычисления формы геоида сводится к получению выражения для

потенциала V.

Выражение для V получаетс

ения F единичной массы m

= 1 элементом массы

жести r равно:

dmm

GF ==

де G

(2.3)

г = 6,666·10

-8

-1

см

– постоянная тяготения. Тогда потенциал притяжения Земли в

точке вне ее, на расстоянии r от ее центра будет равен:

∫

, (2.4)

где интегрирование проводится по всему объ му Земли.

Если бы Земля была точной сферой радиуса R

со сферически-симметричным

ределением плотности, т гравитационный потенциал на ее поверхности был бы в

очности равен:

расп о

V =

, (2.5)

где

М – масса планеты.

Как видно из соотношения (2.1), реальная Земля всего на 1/300 отклоняется от

ой с центром Земли и с осями,

аправленными вдоль главных моментов инерции, первый полином Лежандра

= 0, то

обавление второго члена разложения, содержащего второй полином Лежандра

приводит к выражени

сферы, поэтому в первом приближении к основной части потенциала (2.5) достаточно

добавить следующий поправочный член в выражении для

V через сферические функции -

олиномы Лежандра. Так как в системе координат связаннп

ю:

⎥

⎦

⎢

⎣

⎤

⎡

RGM

Θ−= )(cos)(1

де

, (2.6)

−Θ

- второй полином Лежандра,

cos

)(cos

=ΘP

−=Θ

~0012,0

≈

−

, (2.7)

и С

оответственно.

Окончательно, в пер го члена в

разложении потенциала по

получаем в виде:

А – моменты инерции Земли относительно осей, проходящих через экватор и полюс

вом приближении, с учетом первого ненулево

сферическим функциям, выражение для геопотенциала

⎭

⎬

⎫

⎩

⎨

⎧

⎥

⎦

⎤

⎢

⎣

⎡

−−

ϕωϕ

22222

sin

)

sin

()(1 r

. (2.8)

Как видно из соотношения (2.7), величина I

является малой, порядка величины

зностей

ежду

сжатия Земли. Следовательно, в каждой точке поверхности Земли значения ра

м радиусами «приближенного» геоида r и сферы R

также должны быть небольшими.

Поэтому тело, создающее потенциал (2.8), стало называться сфероидом Клеро или просто

сфероидом

Выражение для коэффициента I

(2.7) и геопотенциала (2.8) в том же приближении

и с той же точностью, очевидно, может быть переписано в следующем виде, в котором

они, как правило, и используются:

(2.7.1)

−

⎭

⎬

⎩

⎨

⎥

⎦

⎢

⎣

−−

ϕωϕ

)

)(1 r

. (2.8.1)

В полученной

⎫⎧

⎤

⎡

22222

sin

(

aGM

формуле (2.8.1), полагая значение геопотенциала равным ускорению

тяжести на экваторе, и решая полученное уравнение относительно радиуса,

удерживая лишь малые первого по ля сфероида

Клеро [Магницкий, 1965, с. 200-202; Бровар, Магницкий, Шимберев, 1961, с. 71-72]:

где

силы

рядка, получаем в явном виде уравнение д

)sin1(

ϕα

−= ar

, (2.9)

−

При учете малых следующего Дарвина-

Де Ситтера [Жарков, Трубицын, 1980

порядка получаем уравнение для сфероида

, с. 283-284, 300-301]:

⎥

⎦

⎤

⎢

⎣

⎡

−+−=

ϕαϕαϕ

2sin)

(sin1)(

kar

де поправочный параметр k, характеризующий отличие уровенных поверхностей от

точного эллипсоида вращ

ения, является малой величиной.

Фигура и распределение массы внутри Земли

[Тр 209-211]

строения Земли большое значение имеет величина

ухин, Показеев, Куницын, 2004, с. 17-18; Магницкий, 1965, с. 200-2002; 2006, c.

Для проблемы внутреннего

среднего момента инерции

2AC

, (2.10)

которая с учетом величин средней плотности

и данных се

йсмологии о

главастроении Земли позволяет получить распределение плотности в недрах планеты ( 5).

В случае постоянной плотности планеты ее безразмерный момент инерции

∗

равен

4,0

∗

I . (2.11)

Если с глубиной плотность увеличивается, то

∗∗

< II

, если ум

0 0

Значение

∗

еньшается, то

∗∗

для Земли равно:

3315,0=

∗

I , (2.12)

что указывает на существенное увеличение плотности в недрах Земли с глубиной.

Впрочем, имеется и другая точка зрения на связь параметра

∗

со строением Земли.

Так Дж.Ф. Эверден [1997] полагает, что Земля негидростатична и, как следствие, значение

параметра

∗

ничего е говорит о распределении плотности внутри Земли. Однако В.В.

Кузнецов [2008, с. 219-221] полагает, что выводы Эвердена слишком категоричны, они

противоречат геофизическим результатам, а сам парадокс Эвердена может быть разрешен

в рамках модели горячей Земли (см. главы 1 – «Модел горячей Земли», и 12 – «Форма

Земли и геодинамика»).

Ускорение силы тяжести g находится

из выражения:

gradWg

−

. (2.13)

Выражения для его азимутальной

∂

и радиальной

∂

−=

составляющих

∂

приводят к соотношению:

)()(

∂

, (2.14)

из которого на основании (2.8), (2.8.1) и (2.14) можно установить связь межд ем у g и сжати

Земли ε:

⎥

⎦

⎤

⎢

⎣

⎡

−+=

)

(2.15)

где

sin

)

. (2.16)

Уравнение (2.15) впервые было получено А. Клеро в 1743 г. (теорема Клеро о силе

тяжести [Буллен, 1978, с. 56-57; Грушинский, 1976, с. 198]), его можно переписать более

просто:

)sin1(

ϕβ

, (2.17)

где

εβ

−= q

Таким образом, сила тяжести в любой точке земного шара обусловлена:

ого сфероида (первое сла - притяжением всего земн гаемое в (2.16)) и центробежной

силой ( торое слагаемое в (2.17)),

работки триангуляций, на который

относя

и и предписываемых

практи т

у г и р

ференц-эллипсоид по измерениям на

небольшой территории, то параметры эллипсоида будут получаться неуверенно. Поэтому

исторически сложилось так, что большинство исследователей стремились построить

референц-эллипсоид по возможности по большему материалу и, по возможности,

приближающийся к общеземному.

Наиболее широкую известность и практическое применение получили следующие

референц-эллипсоиды.

Эллипсоид Бесселя, выведенный в 1841 г. на основании европейских, индийских и

перуанских градусных измерений:

- влиянием рельефа местности, определяемой зависимостью величины угловой

скорости вращения от высоты точки на поверхности,

- неравномерным распределением масс, в основном, в земной коре, величина

которого определяется

значением коэффициента I

(второе слагаемое в (2.16)).

Ре еренц-эллипсоид. Эллипсоид Красовского.

Международный эллипсоид [Грушинский, 1976, с. 102-104]

Определение. Эллипсоид, принятый для об

тся или редуцируются все геодезические измерения, называется референц-

эллипсоидом или эллипсоидом относимости [Грушинский, 1976, с. 22-23].

Выполнение геодезических работ на территориях больших стран с соблюдением

точностей, достижимых современными техническими средствам

ческими потребностями, требует ус ановления специального, наилучшим образом

отвечающего рассматриваемой области эллипсоида относимости

Для нификации еодезическ х измерений на всей Земле удобно пост оить общий

земной эллипсоид, т.е. такой эллипсоид, при котором условие минимума отклонения

квадратов высот геоида выполняется для всей Земли в целом. Такой эллипсоид лучше

всего представляет реальную Землю. Однако для построения такого эллипсоида требуется

выполнять геодезические наблюдения на всей Земле, т

.е. надо иметь однородную

геодезическую сеть. В рамках классической геодезии это практически невозможно, т.к.

нельзя провод ть геодезические измерения в океанах. Кроме того, следует иметь в виду,

что такой оптимальный эллипсоид для всей Земли может и не быть оптимальным для

данной территории. Однако если строить ре

6377397

м,

153,299/1

. Этот эллипсоид получил

широкое распространение в европейских геодезических работах. В частности, в России он

применялся до вывода в 1940 г. эллипсоида Красовского.

В 1866 г. Кларком был выведен эллипсоид, получивший название эллипсоида

Кларка:

м,

6378206=a

979,294/1=

. При выводе использованы градусные измерения

западноевропейские, русские, индийские, перуанские. Этот эллипсоид применялся во

Франции и ее колониях. В 1880 г. Кларком был выведен другой эллипсоид, который

получил применение в США и Канаде:

6378249

м, 466,293/1

В 1924 г. был принят в качестве междун эллипсоид, выведенный

Хейфордом в 1909 г. в основном по американским

м,

ародного

градусным измерениям:

6378388=a

0,297/1=

В 1940 г. под руководством крупнейших советских геодезистов Ф.Н. Красовского и

А.А. Изотова была закончена работа по выводу нового земного эллипсоида, получившего

название эллипсоида Красовского:

6378245

м, 3,298/1

. Для его вывода были

использованы все доступные в то время градусные измерения СССР, США, Индии, а

также гравиметрические съемки, выполненные на территории СССР. В качестве

исходного пункта, по которому был ориентирован этот эллипсоид, принят центр круглого

зала Пулковской обсерватории. В 1946 г., 7 апреля, постановлением Совета Министров

СССР эллипсоид Красовского утвержден в

качестве основного эллипсоида относимости

для всех геодезических работ СССР.

Эллипсоид Красовского, выведенный по большим астрономогеодезическим сетям,

является эллипсоидом, близко представляющим всю Землю. Его элементы близки к

элементам общего земного эллипсоида. Ориентирование его по Пулкову делает его

наиболее подходящим для Европы, Западной Азии и Северной Африки.

В 1967 г. в США выведен

новый -эллипсоид с использованием все

старых

референц х

и большого объема новых градусных измерении, а также мировой

гравиметрической съемки:

6378160=a

м, 247,298/1

. Этот эллипсоид заменил в

качестве международного эллипсоид Хейфорда 1909 г. и получил название

международного эллипсоида 1967 г.

в тя

н и

на массу m, расположенную в точке (r,

), кроме центральной силы тяготения

Понятие о периодах Эйлера и Чандлера, нутации и прецессии, динамическое сжатие

[Стейси, 1972, с. 37-43]

Из уравнения (2.11) идно, что в разложении потенциала силы жести, кроме

члена, пропорционального

-1

, имеется меньший чле , пропорц ональный r

-3

, который

обусловлен сжатием Земли. Этот член зависит от угловой координаты

. Следовательно,

∂

−

действует момент сил

∂

сил, равный по величине и противоположный по направлению. Моменты, возникающие

з-за действия

−

. Поэтому на массу Земли в свою очередь действует момент

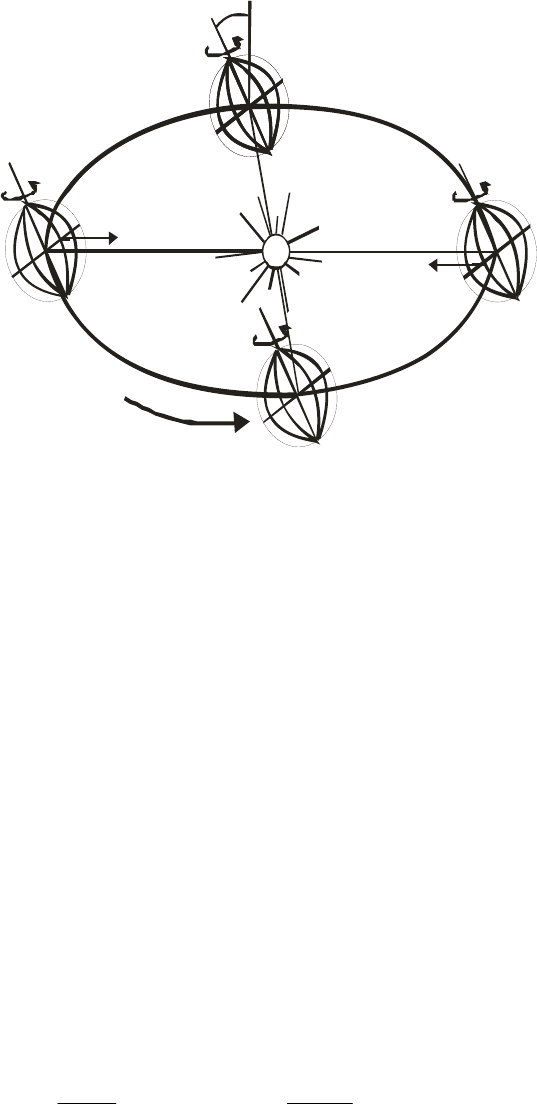
Луны и Солнца на экваториальное вздутие, вызывают прецессию земной

си (рис. 2.2). Период прецессии со

Полное исследование показ накладывается малая нутация,

ли ка

мом

шего момента инерции. Полный момент количества движения

остается постоянным и по величине и по так, что полюс

описывает на ее поверхности круг с центром в точке пересечения оси наибольшего

омента

инерции с поверхностью Земли (рис. 2.3). Ось вращения Земли практически

фиксирована в пространстве и чандлеро ское колебание полюса выражается в

о ставляет 25800 лет.

ывает, что на прецессию

и чания полюса мира

вокруг полюса эклиптики. На са деле имеется несколько

нутаций, возникающих из-за эллиптичности орбит Земли и Луны, расположенных в

разных плоскостях, а также от слабого воздействия других планет.

Независимо от гравитационного взаимодействия с другими телами Земля

испытывает свободную, эйлерову прецессию. В геофизической литературе ее обычно

называют свободной нутацией или чандлеровскими колебаниями

по имени

первооткрывателя. Колебания возникают из-за того, что ось вращения Земли слегка

наклонена к оси наиболь

направлению, а Земля движется

периодических вариациях широты с периодом T

= 430 – 435 суток и переменной

ное полушарие - зима

амплитудой, составляющей, в среднем, α = 0,14

Равнодействие

Северное полушарие - осень

Южное полушарие - весна

Солцестояние

Северное полушарие - лето

Юж

естояние

Северное полушарие - зима

Южное полушарие - лето

Равнодействие

еверное полушарие - весна

Южное полушарие - осен

Солнц

Солнце

энергии вращения приводит к стремлению тела

Рис. 2.2. Причина прецессии земной оси. Гравитационное воздействие Солнца на

экваториальное вздутие создает момен одного и того же направления во время обоих

солнцестояний и не создает никакого момента во время равноденствий.

По аналогии с вращающимся волчком, который можно рассматривать как жесткое

твердое тело, можно получить выражение для периода свободной прецессии Земли. Суть

вычислений заключается в следующем. Полная энергия вращения больше, чем энергия

вращения относительно оси С. Избыток

восстановить состояние симметричного вращения и создает эффективный

гироскопический

момент. Рассматривая его как внешний момент, вызывающий

вынужденную прецессию, получим угловую скорость свободной (эйлеровской) прецессии

жесткой твердой Земли, или, как полагают, теоретический период Чандлера (ch):

= -

, (2.18)

где

- угловая скорость вращения Земли и

– динамическое сжатие, определяемое из

выражения:

51,305

102732,3

≈⋅=

−

. (2.19)

можно видеть из (2.19), теоретическое значение Т

= 2

π/ω

= 305

Как

ch, теор ch

суток не

авно р на практике определенному значению периода Чандлера Т

. Более того,

вариации

широты с частотой

на практике не выявлены. Это может указывать на то, что Землю

нельзя рассматривать как жесткое тело, и, следовательно, чандлеровские колебания,

возможно, связаны не только со свободной прецессией планеты.

Из полученного соотношения (2.19) и из (2.7) находим значение полярного

момента инерции Земли:

3308,0 MaMa

. (2.20)

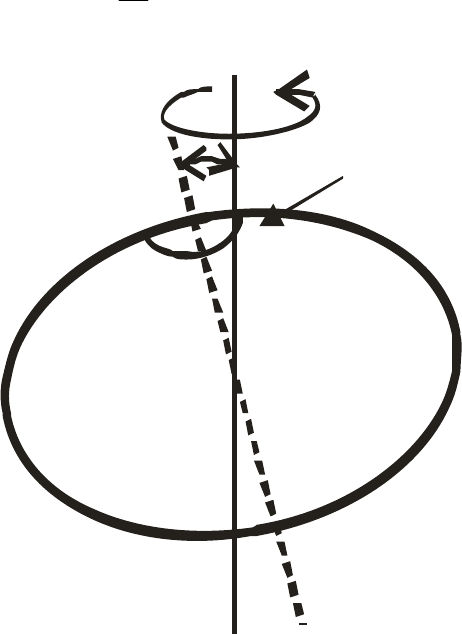
Ось вращени

Траектория оси вращения

на поверхности Земли

Рис. 2.3. Чандлеровское колебание полюса. Периодические изменения широты связаны с тем, что

Земля движется как единое целое, и ее ось вращения, оставаясь неподвижной в пространстве,

описывает конус с раствором 2

вокруг оси наибольшего момента инерции.

Колебания Чандлера и сейсмотектонический процесс

[Викулин, Кролевец, 2001; Vikulin, Krolevets, 2002]

В рамках ротационной модели сейсмического процесса (см. главу 3) исследовалась

природа взаимосвязи сильных землетрясений с прецессией полюса планеты. В результате

были получены следующие результаты.

1. Тектонический процесс, протекающий в районах сейсмически активных поясов

планеты, характеризуется широким спектром частот. Показано, что прецессия полюса

планеты может происходить вследствие изменения формы Земли, вызываемого

колебанием верхней

части литосферы – так называемым «нулевым» колебанием.

Следует отметить следующее. С точки зрения механики, очевидно, что в рамках

ротационной модели возможен и обратный процесс, а именно: перекачка энергии

свободных колебаний планеты в сейсмотектоническое движение.

2. Как оказалось, чандлеровская частота «расщепляется» на две f

ch 1

= 0,835 год

-1

(Т

ch 1

= 437 дней) и f

ch 2

= 0,860 год

-1

(Т

ch 2

= 425 дней). Такой эффект расщепления в рамках

рота ых

ционной модели объясняется различными значениями «нулевых» частот для сам

активных сейсмотектонических поясов планеты, ориентированных меридионально

(тихоокеанской пояс) и широтно (альпийско-гималайской пояс).

3. Распределение значений радиусов траекторий движения полюса планеты по их

числу имеет регулярную «квантовую» составляющую, равную 0

,05. В пересчете на

энергию нутации это значение по порядку величины близко сейсмотектонической

энергии, сбрасываемой в очагах наиболее сильных (М

= 8-9) землетрясений.