Вигура М.А., Соболев А.Б., Рыбалко А.Ф., Рыбалко Н.М. Элементарная математика
Подождите немного. Документ загружается.

I. ЭЛЕМЕНТАРНАЯ МАТЕМАТИКА
3
Федеральное агентство по образованию
ГОУ ВПО «Уральский государственный технический университет – УПИ»
Институт образовательных информационных технологий
I. ЭЛЕМЕНТАРНАЯ МАТЕМАТИКА
Учебное пособие
Научный редактор – доц., канд. физ. - мат. наук О.А. Кеда
Печатается по решению редакционно-издательского совета
Екатеринбург
2005
4
УДК 511(075.8)
ББК 22.13я73
Э-45
Рецензенты:
кафедра физики Уральского государственного лесотехнического университета;
доктор физ-мат. наук, проф. А.П. Танкеев, зав. лабораторией ИФМ УрО РАН
Авторы: А.Б. Соболев, М.А. Вигура, А.Ф. Рыбалко, Н.М. Рыбалко
Э-45 I. ЭЛЕМЕНТАРНАЯ МАТЕМАТИКА: учебное пособие
А.Б. Соболев, М.А. Вигура
, А.Ф. Рыбалко, Н.М. Рыбалко. Екатеринбург: ГОУ
ВПО УГТУ-УПИ, 2005. 81 с.
ISBN 5-321-00633-4
Данная работа представляет собой адаптационный курс элементарной
математики, предваряющий изучение высшей математики, входит в учебно-
методический комплекс дисциплины ЕН.Ф.01.”Математика” для студентов
ММФ, СТФ, МТФ, содержит изложение основных понятий и методов
решения задач, справочный материал
по элементарной математике и задания
для самостоятельной работы.
Рекомендовано Уральским отделением Учебно-методического объединения
вузов РФ в области строительного образования в качестве учебного пособия
для студентов строительных специальностей направления 6533500
“Строительство” всех форм обучения
Подготовлено кафедрой высшей математики
УДК 511(075.8)
ББК 22.13я73
ISBN 5-321-00633-4 © ГОУ ВПО «Уральский государственный
технический университет – УПИ»,2005
5
ОГЛАВЛЕНИЕ
1. АРИФМЕТИКА И АЛГЕБРА……………………………………………..……..6
1.1. Действительные, рациональные и иррациональные числа……………..6
1.2. Числовые неравенства и их свойства……………………………….……6
1.3. Дроби……………………………………………………………………….7
1.4. Пропорции………………………………………………………………….8
1.5. Проценты…………………………………………………………………...8
1.6. Степени и корни…………………………………………...………………8
1.7. Модуль (абсолютная величина)…………………………………………10
1.8. Формулы сокращенного умножения…………………………………....11
1.9. Иррациональные выражения…………………………………………….11
1.10. Сравнение чисел………………………………………………………...12
1.11. Тождественные преобразования алгебраических выражений.............12
1.12. Выделение полного квадрата в квадратном трехчлене………………13
1.13. Прогрессии………………………………………………………………14
2. ФУНКЦИИ, ИХ
СВОЙСТВА И ГРАФИКИ………………………………..…15
2.1. Основные понятия………………………………………………………..15
2.2. Линейная функция………………………………………………………..16
2.3. Квадратичная функция……………………………………………...........17
2.4. Степеннные функции…………………………..………………….……..18
2.5. Дробно–линейная функция………….………………..…………..……..20
2.6. Показательная функция……...…………………..……………………....21
2.7. Логарифмы и их свойства………………..…………………...…….……22
2.8. Логарифмическая функция……….……………..…………………….…22
2.9. Геометрические преобразования графиков функций………………….22
3. РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ……..………………….…………………...24
3.1. Линейные уравнения …….…………………………….………………..24
3.2. Квадратные уравнения …………………………………….……………24
3.3. Теория многочленов…………………..…………………………………25
3.4. Кубические уравнения…………..………………………………………27
3.5. Дробно–рациональные уравнения…………………………...................27
4. РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА…………………………………………..28
4.1. Решение
квадратных неравенств……………………..………………....28
4.2. Дробно-рациональные неравенства……………………………………..28
4.3. Системы рациональных уравнений……….…………………………….29
5. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ…………………………………………..31
6
5.1. Равносильные преобразования иррациональных уравнений………….31
6. ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА………………..………………………32
7. УРАВНЕНИЯ, СОДЕРЖАЩИЕ ЗНАК АБСОЛЮТНОЙ ВЕЛИЧИНЫ…...…33
8. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ЗНАК АБСОЛЮТНОЙ ВЕЛИЧИНЫ…..34
9. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ……………………………..……………....35
9.1. Равносильные преобразования показательных уравнений...………….35
9.2. Равносильные преобразования степенно-показательных уравнений...36
9.3. Равносильные преобразования показательных неравенств…………...36
10. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ……………………..…….…………...37
11. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА………………...……..……………39
11.1. Равносильные преобразования логарифмических неравенств………39
12. ТРИГОНОМЕТРИЯ.…………………………….……………………………...41
12.1. Тригонометрические функции произвольного аргумента
……..…….41
12.2. Основные формулы……………………………….…………………….42
12.3. Свойства и графики тригонометрических функций………………….47
12.4. Тригонометрические уравнения……………………………………….49
12.5. Тригонометрические неравенства……………………………………..52
12.6. Обратные тригонометрические функции……………………………..53
13. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА…………………………...55
13.1.Таблица производных…………………………………………………...55
13.2. Правила дифференцирования…………………………………………..55
13.3. Уравнение касательной и нормали к графику функции………..…….55
13.4. Исследование функций с помощью производной…………………….56
13.5. Схема построения графиков…………………………………..………..56
14. ВЕКТОРНАЯ АЛГЕБРА………………………………………….…………....56
15. ПЛАНИМЕТРИЯ………………………………………………….……………59
16. СТЕРЕОМЕТРИЯ……………………………………………….….…………..63
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ
РАБОТЫ……………………..………64
7

СПИСОК НЕКОТОРЫХ ОБОЗНАЧЕНИЙ И СОКРАЩЕНИЙ
1.
– элемент принадлежит
множеству
aA∈
A
.
2. a – не принадлежит A∉ a
A
.
3.
A
B⊂ –
A
– подмножество
множества
B
,
A
содержится в
B
,
B
содержит
A
.
4.
– пустое множество.
∅
5.
A
B∪ – объединение
множеств.
6.
A
B∩ – пересечение
множеств.
7.
∃
– квантор существования,
aA∃∈ – читается "существует
элемент
, принадлежащий
множеству
a
A
".
8.
– квантор всеобщности,
∀
aA∀∈ – читается "для
каждого элемента
,
принадлежащего множеству
a
A
".
9.
∞
– бесконечность.
10.
A
B⇒ – из следует .
A
B
11.
A
B
⇔
–
A
эквивалентно
B
,
A
равносильно
B
.
12.
12
1
n
jn
j
aaa a
=
=
+++
∑
… .
13.
12
1
n
jn
j
aaa a
=
=
⋅⋅⋅
∏
… .
14.
1
1
n
n
e lim
n
→∞
⎛⎞
=
+=
⎜⎟
⎝⎠
2 718281828
,...
=
– основание
натуральных логарифмов.
15. ОДЗ – область допустимых
значений выражения.
ЧИСЛОВЫЕ МНОЖЕСТВА:
N – множество натуральных чисел
{
}
12N,,,n,
=
……;
Z
– множество целых чисел
{
}
012Z,,,,n,
=
±± ±……;
Q
– множество рациональных чисел (вида
0
p
,p,q Z,q
q
∈
≠
);
I
– множество иррациональных чисел
3
25р
,
,e, ,±± …
.
R
– множество действительных (вещественных) чисел,
R
QI= ∪
.
Числовые промежутки:
интервал: ;
()
baxbxa ,, ∈<<
отрезок (сегмент):
[
]
baxbxa ,,
∈
≤≤
;
полуинтервал (полусегмент):
(
]
[
)
⎩
⎨
⎧
∈<≤
∈≤<
;,,
;,,
baxbxa
baxbxa
луч:
[
)
(
)
(
]
()
⎩
⎨
⎧
≤∞−∈≤<∞−
≥∞∈∞<≤
.,,
;,,
bxbxbx
axaxxa
8
1.АРИФМЕТИКА И АЛГЕБРА
1.1. Действительные, рациональные и иррациональные числа
ОПРЕДЕЛЕНИЕ. Числа 1, 2, 3,... называются натуральными и обозначаются
.
{}{ }
...,3,2,1== nN
ОПРЕДЕЛЕНИЕ. Числа
{}
NnnZ
∈
±
−
−
= ,...,,...,2,2,1,1,0
образуют
множество
целых чисел.
Натуральное число, большее единицы, называется
простым, если оно не
имеет других делителей, кроме единицы и самого себя. Например, 2, 3, 5, 7, 11 –
простые числа. Натуральное число называется
составным, если оно имеет хотя
бы один делитель, отличный от единицы и самого себя. Например, числа 4, 12,
28 – составные. Натуральное число называется
четным, если оно делится
(нацело) на число 2, и
нечетным, если оно не делится на 2.
ОПРЕДЕЛЕНИЕ. Числа вида
n
m
, где
NnZm
∈
∈
,
, называются
рациональными дробями. Дроби
n
m
и
Zk
kn
km
∈,
определяют одно и то же
число.
Множество целых чисел является подмножеством множества
рациональных чисел
.
)1( =n
ОПРЕДЕЛЕНИЕ. Если
nm <
, то рациональная дробь называется
правильной, если
nm ≥
– неправильной.
Рациональные дроби представляются в виде конечной или бесконечной
периодической десятичной дроби путем деления числителя на знаменатель.
ОПРЕДЕЛЕНИЕ. Совокупность целых и дробных чисел (положительных и
отрицательных), а также число нуль составляют
множество рациональных
чисел Q
:
⎭
⎬
⎫
⎩
⎨
⎧
±±=
n
m
nQ ,,0
, которые могут быть представлены в виде конечной или
бесконечной периодической десятичной дроби.
ОПРЕДЕЛЕНИЕ. Числа, выражающиеся бесконечной непериодической
десятичной дробью, составляют
множество иррациональных чисел I.
(Например,
2 ,
3
3 ,
π
, . ) e
ОПРЕДЕЛЕНИЕ. Числа рациональные и иррациональные составляют
множество действительных чисел.
Между множеством действительных чисел и множеством точек числовой
прямой существует взаимно-однозначное соответствие.
1.2.Числовые неравенства и их свойства
При сравнении двух действительных чисел и возможны три случая: a
b
1)
равно ( ), если a
b
ba = 0
=
− ba
; 2) больше ( ), если ; a
b
ba >
0>− ba
3)
меньше ( ), если a
b
ba <
0
<
− ba
. Объединяя случаи 1) и 2), получаем
неравенство 4)
не меньше ( ); случаи 1) и 3) – неравенство 5) не a
b
ba ≥
a
9
больше
( ). Неравенства 2) и 3) называются строгими, 4) и 5) –
нестрогими.
b
ba ≤
Рассмотрим свойства числовых неравенств. Доказательства этих свойств
опираются на следующие утверждения:
1) сумма положительных чисел положительна, 2) произведение
положительных чисел положительно, 3) число, противоположное
положительному, отрицательно. (Напомним, что противоположным числу
называется такое число ( ), что
a
a−
(
)
0
=
−
+
aa ).
1.
Если , то . ba > ab <
2. Если
и , то (свойство транзитивности). ba > cb > ca >
3.
Если , то , где с – любое действительное число. ba > cbca +>+
Следствие. Любое слагаемое можно переносить из одной части
неравенства в другую с противоположным знаком.
4.
Если и , то . ba > 0>c bcac >
5. Если и , то . ba > 0<c bcac <
6.
Если и , то . ba > dc > dbca +>+
Следствие. Неравенства одинакового смысла можно почленно складывать.
7.
Если и , то . ba > dc < dbca −>−
Следствие. Неравенства противоположного смысла можно почленно вычитать,
оставляя знак уменьшаемого.
8.
Если и , то . 0>> ba 0>> dc bdac >
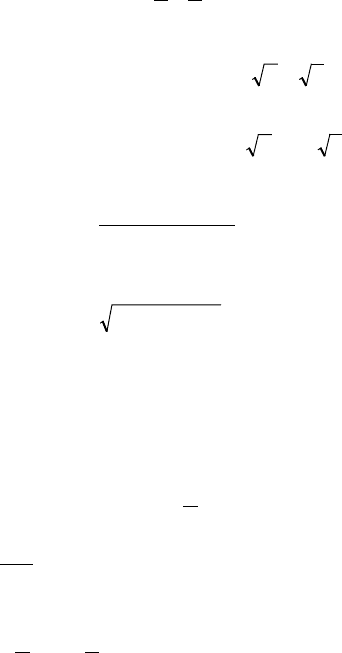
9. Если , то 0>> ba
ba
11
<
.
10. Если и , то . 0≥> ba Nn ∈
nn
ba >
11. Если и , то 0≥> ba Nn ∈
nn
ba > .
12. Если , то . ba > Nnba
nn
∈>
++
,
1212
13. Если и , то ba > Nn ∈
1212 ++
>
nn
ba .
Средним арифметическим действительных чисел называется
число, равное
n
n
aaa ,,,
21
…
n
aaa
n
+
+
+ ...
21
.
Средним геометрическим действительных чисел называется
число, равное
n
n
aaa ,,,
21
…
n
n
aaa ⋅⋅⋅ ...
21
.
1.3.Дроби
ba
b
a
:=
– обыкновенная дробь ( 0,, ≠
∈
bZba ).
n
n
a
a
−
⋅= 10
10
– десятичная дробь ( Nn
∈
).
0,01 = 1 % – процент.
b
a
A
b
a
A +=
– смешанная дробь ( NbaA
∈
,, ).
10
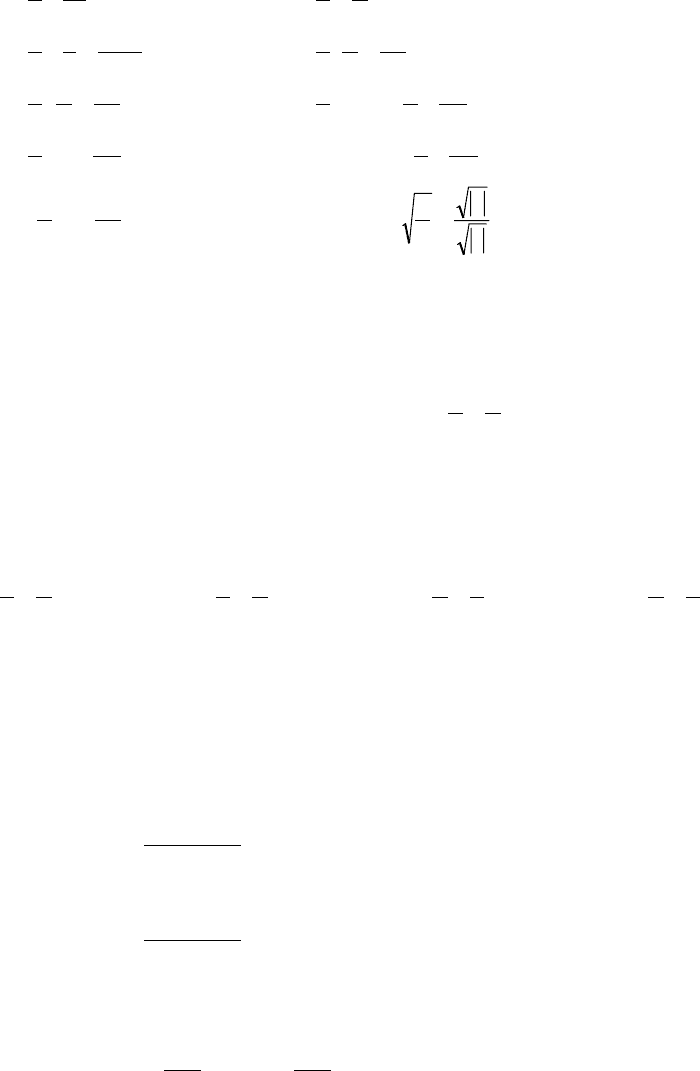
Основные свойства
1.
bc
ac
b
a
=
, ( ). 2. 0≠c
d
c
b
a
=
, если bcad
=
.
3.
b
ca
b
c
b
a ±
=±
. 4.
bd
ac
d
c
b
a
=⋅
.
5.
bc
ad
d
c
b
a
=:
. 6.
b
am
b
a
mm
b
a
=⋅=⋅
.
7.
bm
a
m
b
a
=:
( 0
≠
m ). 8.
a
mb
b
a
m =:
.
9.
n
n
n
b
a
b
a
=
⎟
⎠
⎞
⎜
⎝
⎛
. 10.
n
n
n
b
a
b
a
=
( ). 0>ab
1.4. Пропорции
Частное от деления одного числа на другое называется также их
отношением. Равенство двух отношений
d
c
b
a
=
)0(
≠
bd называется пропорцией,
– крайние члены пропорции, – средние члены. При этом , что
порождает четыре равносильных (при
da, cb, bcad =
0
≠
abcd ) пропорции:
d
c
b
a
=
,
d
b
c
a
=
,
a
c
b
d
=
,
a
b
c
d
=
.
1.5. Проценты
ОПРЕДЕЛЕНИЕ. Процентом
называется сотая часть величины.
ПРИМЕР. Найдите число, которое составляет 115% от 2860.
Искомое число
3289
100
1152860
=
⋅
.
ПРИМЕР. Найдите число, если 12,5% от него равны 3000.
Искомое число
24000
5,12
1003000
=
⋅
.
ПРИМЕР. Найдите выражение одного числа в процентах от другого, а именно,
на сколько процентов увеличилось число 120, став равным 230.
%66,91%100
120
110
%100
120
,110120230 =⋅=⋅
∆
=−=∆
1.6. Степени и корни
ОПРЕДЕЛЕНИЕ.
Степенью числа (
n
a a NnRa
∈
∈
, ) с натуральным
показателем называется произведение множителей, каждый из которых
равен
, ; число называется основанием степени, число –
показателем степени.
n n
a
…
n
n
aaaaa ⋅⋅⋅⋅= a n
Из этого определения следуют основные свойства степени:
11

1)
; 2) .
nmnm
aaa
+
=⋅
()
nm
n
m
aa
⋅
=
ОПРЕДЕЛЕНИЕ. Пусть ZpRa
∈
∈ , . Степень с целым показателем
определяется следующими соотношениями:
p
a p
1)
, если ,
…
m
m
aaaaa ⋅⋅⋅⋅= mp = Nm
∈
;
2)
m
m
a
a
1
=
−
, если и , 0≠a mp −= Nm
∈
;
3)
, если 1
0
=a 0
≠
a ;
4) при
и 0=a 0
=
p или степень с целым показателем не
определена
.
0<p
p
a p
Рассмотрим основные свойства степени с
целым показателем.
Пусть
, , , , , Ra ∈ Rb ∈ 0≠a 0≠b Zn ∈ Zm
∈
. Тогда:
1)
. 2)
nmnm
aaa
+
=⋅
nm
n
m
a
a
a
−
= .
3)
. 4)
()
nm
n
m
aa
⋅
=
(
)
nn
n
baab = .
5)
n
n
n
b
a
b
a
=
⎟
⎠
⎞
⎜
⎝
⎛
. 6)
nn
a
b
b
a
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
−
.
7)
0>a . 8) 00>⇒
n
a
<
a :
9) Если
, то .
10) Если
, то .
11) Если
, , то
⎪
⎩
⎪
⎨
⎧
<⇒+=
>⇒=
.012
,02
n
n
akn
akn
1>a ⇔> mn
mn
aa >
10 << a ⇔> mn
mn
aa <
0>a 1≠a mn =
⇔
.
12)
ba <<0 :
mn
aa =
⎪
⎩
⎪
⎨
⎧
<⇔<
=⇔=
>⇔>
.0
,0
,0
nn
nn
nn
ban
ban
ban
ОПРЕДЕЛЕНИЕ. Число b называется корнем -й степени из числа
(обозначается
n a
n
ab = ), если . Также употребляется название радикал (от
латинского radix - корень).
ab
n
=
Случаи четных и нечетных
нужно рассматривать отдельно.
1)
n
Nkkn ∈= ,2 . Если
k
ab
2
= , то
(
)
0
22
≥==
n
k
bab , поэтому корни четной степени
k
a
2
существуют только для
. 0≥a
ОПРЕДЕЛЕНИЕ. Арифметическим корнем -й степени из
неотрицательного числа
называется неотрицательное число (обозначаемое
n
a b
n
ab = ), такое, что . ab
n
=
Корни четной степени всегда понимаются как арифметические!
Основные свойства арифметических корней.
Пусть
, , , , (0>a 0>b 1>n 1>m 1>k Nkmn
∈
,, ). Тогда:
1)
nk
kn
kn
aaa
+
=⋅ . 2)
n
nk
k
aa = .
3)
nnn
baab ⋅= . 4)
nn
n
ba
b
a
:= .
12
