Вигура М.А., Соболев А.Б., Рыбалко А.Ф., Рыбалко Н.М. Элементарная математика

Медиана треугольника

Медианы треугольника пересекаются в одной точке и делятся точкой

пересечения в отношении 2 : 1, считая от вершины.

Точка пересечения медиан треугольника совпадает с его центром тяжести.

Медиана делит площадь треугольника пополам.

222

ca−

1

22

2

a

mb=+ .

A

R

C B

R

O R

Перпендикуляры, проведенные через

середины сторон треугольника

O – центр описанной окружности;

4

abc

R

S

= .

Прямоугольный треугольник

a и – катеты; – гипотенуза; и – проекции

катетов на гипотенузу;

b c

c

a

c

b

222

cab

+

= – теорема

Пифагора;

1

2

Sab= ;

O

A

b

c

b c

m

c

h

c

a

c

C a B

1

2

Sc=

c

h;

2

ab

r

c

+

−

= ;

2

c

R

=

;

; a ; b ;

2

ccc

hab=

2

c

ca= cb=

2

c

sin cos tg ctgac Ac Bb Ab B= = =⋅ =⋅ ;

c

ab ch= ;

1

2

c

m . cR==

R

B

R

a r

a

R

A a C

r

O

Равносторонний треугольник

2

3

4

a

S

= ; 3aR= ;

23ar= ;

3

6

a

r = ;

3

a

R = .

Окружность, круг

r – радиус окружности; C – длина окружности;

S –площадь круга; ; 2рCr=⋅

2

рSr

=

⋅ .

Сектор, сегмент

r – радиус окружности; l – длина дуги, ограничивающей

сектор;

– площадь сектора; – градусная мера

центрального угла;

сек

S n°

α

– радианная мера центрального угла;

р

180

rn

lr

α

⋅°

==⋅

°

;

2

360

A

R l

O

α

B

2

сек

р 1

2

rn

Sr

α

⋅°

==

°

;

()

2

сегм

sinб

2

AlB AOBl AOB

r

SSS S

α

∆

== − = − .

Центральный угол

A

OB измеряется градусной мерой дуги, на которую он

опирается: AOB AB

α

∠=



. =

60

Вписанный в окружность угол равен половине

центрального угла, опирающегося на ту же дугу, или

дополняет ее до 1 . 80°

C

A O

B

C

A B

D O

Угол между хордой и полукасательной в ее концевой точке

измеряется половиной соответствующего центрального угла.

Произведения отрезков пересекающихся хорд равны:

A

SBS DSCS⋅=⋅.

A

C

D

B

S

B

С Р

A

Если через точку проведены секущая окружности и

касательная, то произведение отрезков секущей равно

квадрату отрезка касательной:

2

CP AP BP

=

⋅ .

Произведения отрезков секущих на их внешние части

равны:

C P

B

A E

D

A

PBP⋅=

и

DPEP⋅.

Углы с вершиной внутри ли вне окружности равны:

2

EDCA

ABC



−

=∠

;

2

DM AF

DKM

+

∠=



.

F

A D

K

B

C E

M

Произвольный выпуклый четырехугольник

1

d и – длины диагоналей;

2

d

B

a d

2

b

A d

1

ϕ

C

d c

D

ϕ

– угол между ними;

S – площадь.

360

A

BCD∠+∠+∠+∠ = °;

12

1

sin

2

Sdd

ϕ

= .

61

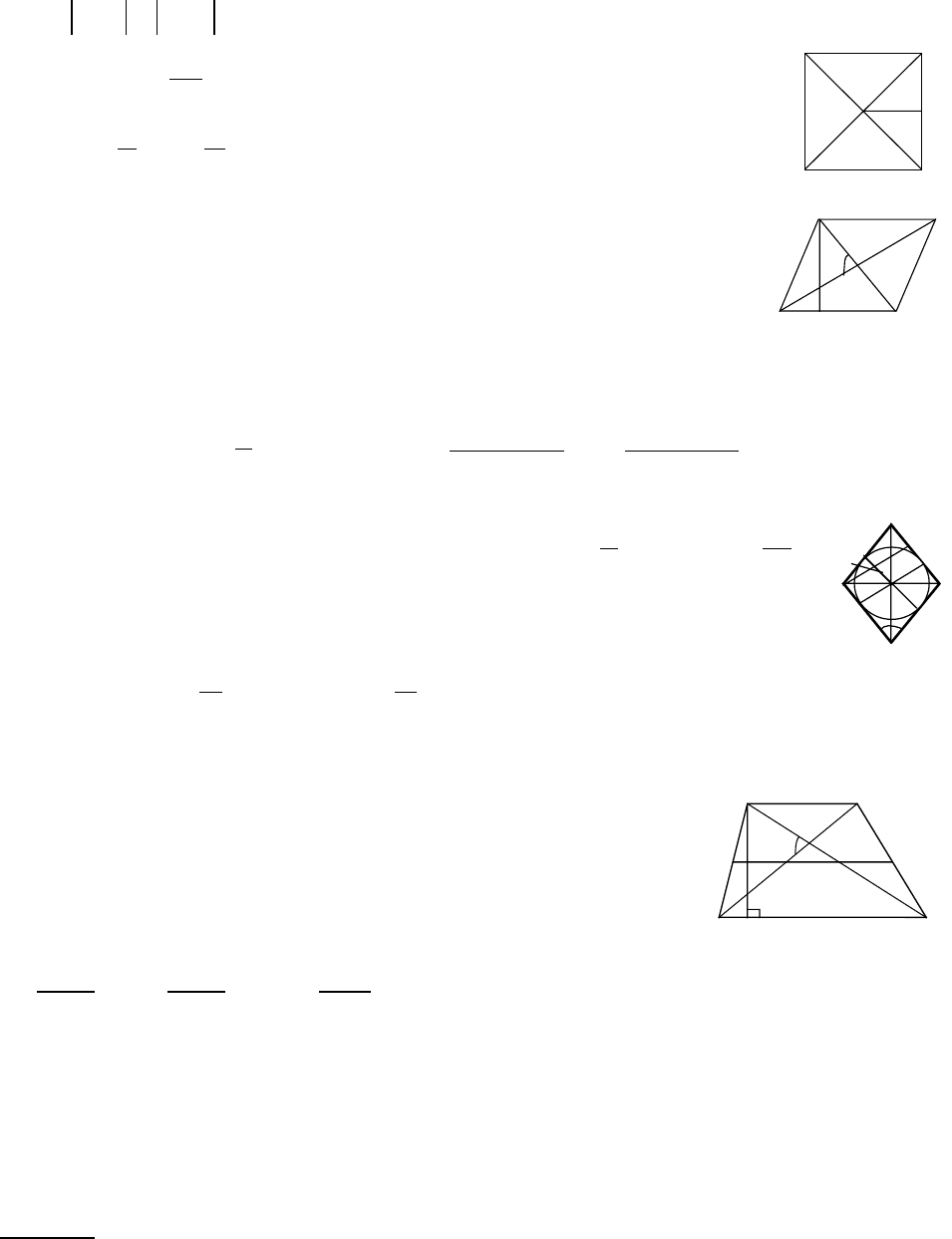
Квадрат

12

ddd==

12

⊥; dd;

a

r

O

B

C

R

a a

A a D

2

d

Sa

== ;

2

a

r

= ;

2

d

R

= .

Параллелограмм

B

C

d

1

b

ϕ

h

a

O d

2

A a D

a и b – длины смежных сторон параллелограмма

A

BCD ;

A

– величина угла между этими сторонами; – высота,

опущенная на сторону ;

d, – длины диагоналей;

a

h

2

d

b ab ABC=+− ∠

a

1

S – площадь параллелограмма;

sin

a

hb A=⋅ ; da ;

222

1

2cos

(

)

22 22

12

2dd ab+= + ; ;

;

a

Sah=⋅

sinS ab BAD

=∠

12

1

sin

2

Sdd AOB=∠

;

22 22

tg tg

42

AC BD AB AD

AOD

−−

==∠

h

2

Sa

SA

.

Ромб

D

B

a a

h

a

r

A O C

a

α

12

dd⊥ ; ;

a

Sa=⋅ sinB

=

;

12

1

2

Sd

=

d

;

2

a

h

r

=

2

;

22

12

4dd a+=

O – центр вписанной окружности;

1

2sin

2

da

α

= ;

2

2cos

2

da

α

= , б

A

DC

=

∠ .

ТРАПЕЦИЯ

a и b – основания;

l

B b C

ϕ

c d

h d

1

d

2

A

aD

c и d – боковые стороны;

h – высота;

и d – длины диагоналей;

1

d

2

l – средняя линия;

ϕ – угол между диагоналями;

S – площадь;

2

ab

l

+

=

;

2

ab

Sh

+

=⋅

;

12

sin

2

dd

S

ϕ

= .

Если

, то в трапецию можно вписать окружность.

abcd

+=+

Описать окружность можно только в том случае, если cd

=

.

Многоугольники

n – число сторон или вершин;

(

)

0

2180n − – сумма внутренних углов;

(

)

3

2

nn−

– число диагоналей.

62

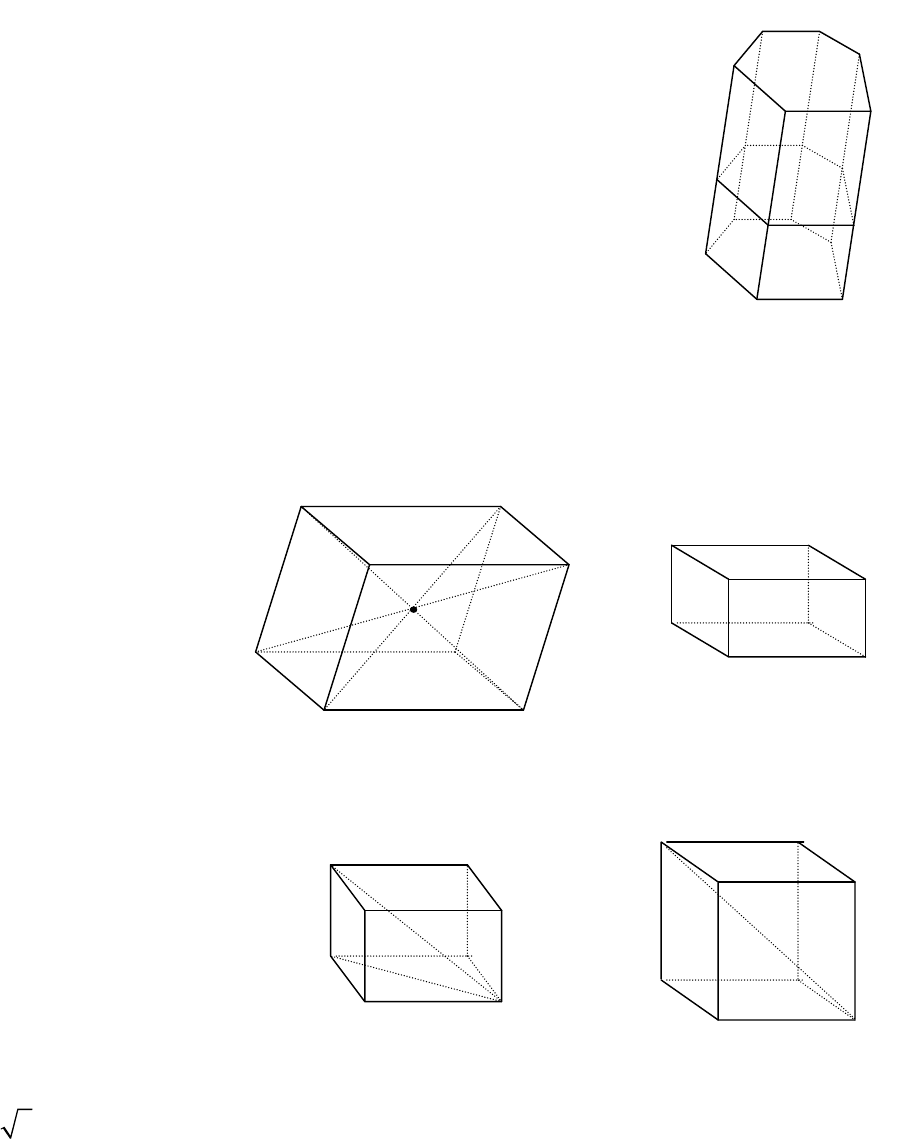
16. СТЕРЕОМЕТРИЯ

Произвольная призма

l – боковое ребро;

f

e

d

c

b

a

l

F

1

E

1

D

1

C

1

B

1

A

1

F

E

D

C

B

A

P – периметр основания;

S – площадь основания;

H

– высота;

сеч

P – периметр перпендикулярного сечения;

бок

S – площадь боковой поверхности;

V – объем;

сеч

S – площадь перпендикулярного сечения.

сеч

Sl⊥ ; ;

сеч

VS=⋅l

l

осн

VS H=⋅; .

бок сеч

SP=⋅

Параллелепипед. Прямой параллелепипед

бок сеч

SP=⋅;

A

BCD –

параллелограмм;

; VSH=⋅

бок

SP=⋅l;

VSl=⋅.

Прямоугольный параллелепипед и куб

A

BCD –прямоугольник;

l

d

D

1

C

1

B

1

A

1

O

B

C

D

A

l

D

C

B

A

D

1

C

1

B

1

A

1

a

c

b

d

a

D

C

B

A

D

1

C

1

B

1

A

1

d

a

D

C

B

A

D

1

C

1

B

1

A

1

A

BCD – квадрат;

()

бок

2Sab=+⋅c

2

;

2

бок

4Sa= ;

2

пов

6Sa= ;

Vabc= ;

222

dabc=++.

3

Va= ;

3da= .

63

Произвольная пирамида

S – площадь основания;

H

– высота;

V – объем;

бок

S – площадь боковой поверхности;

α – угол между боковой гранью и плоскостью

основания;

β – угол между боковым ребром и плоскостью

основания;

l – высота боковой грани (для правильной пирамиды -

апофема);

β

α

l

O

H

A

E

D

C

B

S

β

α

l

O

A

D

C

B

S

l

h

D

1

A

1

B

1

C

1

O

A

D

C

B

l

P – периметр основания;

осн

1

3

VS=⋅H;

()

3

бок осн

r

VSS=+

,

где r – радиус вписанного шара.

Правильная пирамида

A

BCD – правильный многоугольник;

бок

cosбSS=⋅ ;

бок

1

2

SP=⋅l.

Правильная усеченная пирамида

1

S и – площади оснований;

2

S

h – высота; V – объем;

l – апофема;

12,

aa, и – стороны и периметры оснований;

1

P

2

P

12

h,h – высоты пирамид с общей вершиной;

()

12

1

2

бок

SPP=+l⋅;

()

2112

1

3

VhSSSS=+⋅+;

22

111

22

222

Sah

==

.

Цилиндр

R

O

1

H

R

– радиус основания;

бок

S – площадь боковой поверхности;

п

S – площадь полной поверхности;

V – объем;

бок

2рSRH=

(

;

)

п

2рSRRH=+ RH; V

2

р

=

.

64

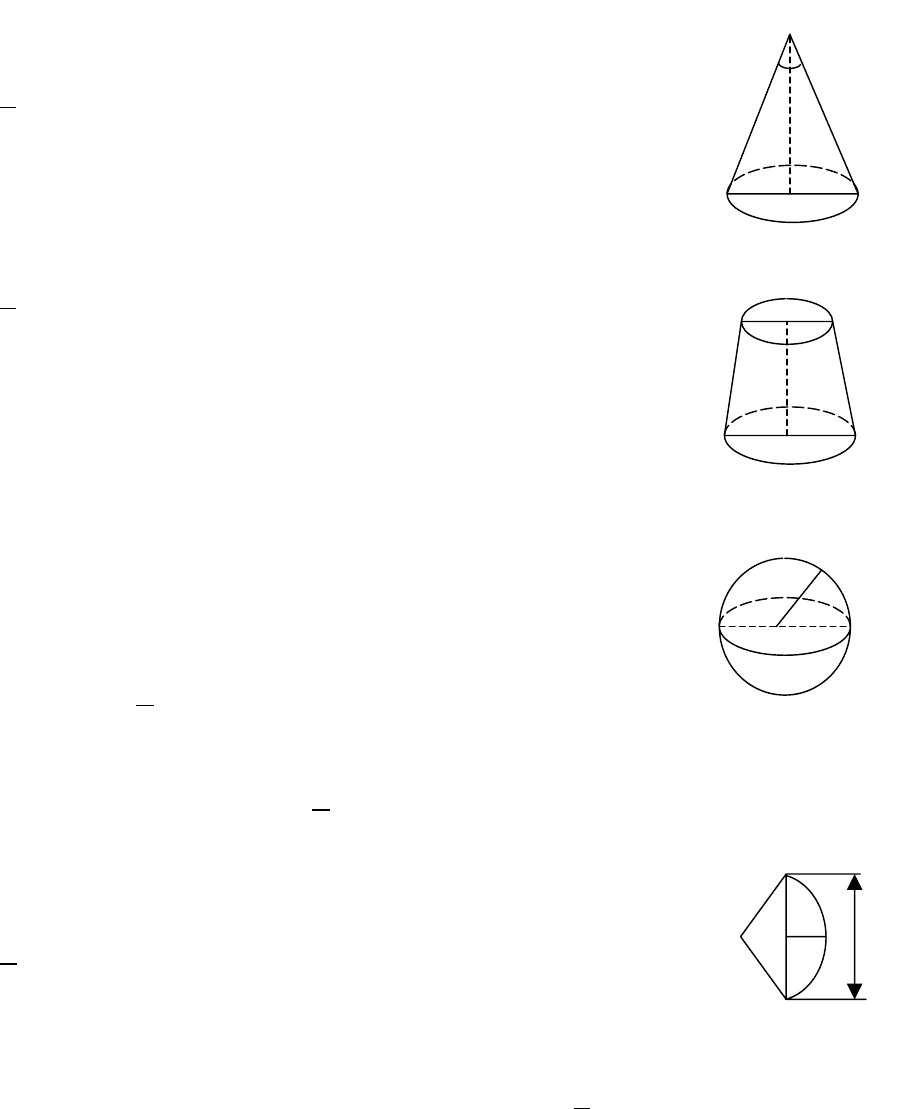
Конус

α

A

l

R

H

R

O

S

бок

рSRl=

(

;

)

полн

рSRRl=+;

2

1

р

3

VR= H.

Усеченный конус

()

22

1

р

3

VHRRrr=++;

r

l

H

R

O

R

(

)

бок

рSlR=⋅⋅ +r;

(

)

22

п

ррSlRrRr=+++р.

Шар. Шаровой сектор

S – площадь поверхности шара;

R

– радиус шара;

h – высота сегмента;

V – объем;

2

4рSR= ;

3

4

р

3

VR. =

Шаровой сектор:

(

)

шар.сек

р 2SRha=+;

2

шар.сек

2

р

3

h=VR.

Шаровой слой:

(

)

22

пов 12

р 2SRHr=++r;

()

(

)

22 2

12

1

р 3

6

VH rrH=++

=+= +

,

где

и – радиусы сечений шара.

1

r

2

r

2a

h

O

R

Шаровой сегмент:

2

шар.сегм сегм осн

2ррSSSRha;

2

шар.сегм

1

р

3

Rh

⎛⎞

=−

⎜⎟

⎝⎠

Vh

.

65

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Задание 1. Арифметика

Вариант 1

1. Вычислите:

.

5,5

3

22

25

3

288,1125,08,1:

5

1

137,26 ⋅+

⎟

⎠

⎞

⎜

⎝

⎛

++

⎟

⎠

⎞

⎜

⎝

⎛

−

Ответ: 20.

2.

.

⎜

⎛

66

6

7

49

99

:

49

23

7

8

65

18

36

17

18

41

+

⎟

⎠

⎞

⎜

⎝

⎛

−+⋅

⎟

⎠

⎞

⎝

−

Ответ: 2.

3.

.

9,6125,08,0

7

4

25

:53,2

+⋅

⋅

⎟

⎠

⎞

⎜

⎝

⎛

+

Ответ: 3,1.

4. Найдите x из пропорции:

.

9

124

2

33

25

4

6

5

:25,0

5

56,0

75

108

9

−

=

⎟

⎠

⎞

⎜

⎝

⎛

+

x

Ответ: 70.

5. Найдите число, если 8% его равны

24.

Ответ: 300.

6. Вычислить:

.

18

5

68

2

0

−

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⋅−

Ответ: 0,25.

7.

.)2()125,0()2(

02/1162/1

+−

−−−

Ответ: 1.

8.

.

245

4

2

32

1

423

5

2

57

+

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅⋅

Ответ: 1,6.

9.

.

5

2763

2

12

3

22

−

Ответ: 6.

10.

.

3

6

3

16

)63163(

)4970100)(710(

2

333

3/13/1

⎟

⎠

⎞

⎜

⎝

⎛

+−

++−

Ответ: 0,03.

Вариант 2

1. Вычислите:

.70:

2

1

3

5

1

425,29:300004,0

8

1

4

⎟

⎠

⎞

⎜

⎝

⎛

−+

⎟

⎠

⎞

⎜

⎝

⎛

⋅−

Ответ: 0,11.

2.

.

6

5

:75,317:

4

17

2

3

16

10

+

⎟

⎠

⎞

⎜

⎝

⎛

⋅+

Ответ: 5,5.

3.

.

5,1:5,1

20

33

05,0:7,1

5

16

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

Ответ: 300.

4. Найдите x из пропорции:

.

4

99

:7,7

15

2

26

1

18

13

72

5

16

3

25

53

50

94

+

=

⋅−

⋅

⎟

⎠

⎞

⎜

⎝

⎛

+

x

Ответ: 8.

5.Найдите число, если 140% его

равны 182.

Ответ: 130.

6. Вычислить:

.18312

6

1

:

2

1

4

3

2

3

024

3

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅−

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

+

−

Ответ: 29,65.

7.

()

.

2

3

2

0

8

4/1

−

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

+

Ответ: 0,81.

8.

.

13

1

160

49

1

56

16

7

1

2

4

2

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅

⎟

⎠

⎞

⎜

⎝

⎛

Ответ: 48.

9.

.

)2338(15

244

25

12

3

22

−

Ответ: 0,4.

10.

.

6427

)827)(87277(

2

2/12/1

−

+−

Ответ: 0,2.

Задание 2. Алгебра

Вариант 1

1.Упростите выражение:

.

33

22

3223

ba

babbaa

−

+++

Ответ:

.

)(

2

ba

−

+

2.Выполнить действия:

.

224

2

a

aa

−−

++

Ответ: 4.

3.

.

1

2

x

a

axa

x

+

Ответ:

.

1

a

4.

.

4

33

22

2

ba

a

ab

abba

baba

b

−

+

−

+

++

Ответ:

.

65

)(

22

2

baba

ab

++

−

5.

.

93

9

27

912

3

:1

)3(

9

23

2

⎟

⎠

⎞

⎜

⎝

⎛

++

+

−

+

−

− aaa

aa

a

Ответ: –1.

6.

.

2

)(1

1

)(1

22

1

⎟

⎠

⎞

⎜

⎝

⎛

+−

−

+−

++

−

ax

xa

Ответ:

.

2

)1(

2

ax

xa ++

7.

.

2

)(:

5,05,0

5,0

5,05,0

5,15,1

ba

b

baba

ba

+

+−

⎟

⎠

⎞

⎜

⎝

⎛

−

+

Ответ: 1.

8.

.:

11

2

ba

a

baba

−

⎟

⎠

⎞

⎜

⎝

⎛

+

−

Ответ: 2.

9.Упростить выражение и вычислить

его при заданном значении

параметра:

⎟

⎠

⎞

⎜

⎝

⎛

−

+

+++

262

153

:)215185(

3

33

m

mmmm

при

.3=m

Ответ: 6.

10.

1

822

22618

3

−

+++

aaa

при .2=a

Ответ: 1.

Вариант 2

1. Упростите выражение:

.

))((

2222

ba

bababa

−

+−−

Ответ:

.

33

ba +

2.Выполнить действия:

.

1

32

2

b

bb

−

−+

Ответ: 3.

3.

.

22

3322

ba

−

Ответ:

.

ba

ab

+

4.

.

62

1

9

2

3

1

222

yx

xyxyx

−

+

−

+

Ответ:

.

)3(2

2

yxx

x

−

5.

.

1

5

51

5

:

1

5

15

5

22

+

−

+

⎟

⎠

⎞

⎜

⎝

⎛

+

−

+

c

cc

c

Ответ:

.1

−

c

6.

.

2

1

)()(

1

2

122122

−

−−

⎟

⎠

⎞

⎜

⎝

⎛

−

+−−

++−

x

b

bxbx

Ответ:

2

2b

x

.

7.

.

1

:

1

2/1

−

+

⎟

⎠

⎞

⎜

⎝

⎛

−

+

−

a

Ответ: 2

8.

.

)(

1

:1

xaxaxaxaxa

xaxa

+−−+

⎟

⎠

⎞

⎜

⎝

⎛

+

−−+

−++

Ответ:

)(2 xa

+

.

9.Упростить выражение и вычислить

его при заданном значении

параметра:

)1(4

6

3

nnn

nnnn

+

при

.

64

5

=n

Ответ: 3,2.

10.

(

)

2/13

12

333

)6(

)3(

1

3

9

:273

−

−−

−

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

+

−

a

aa

при

.218=a

Ответ: 36.

Задание 3. Функции и их графики

Вариант 1

Построить графики функций.

1.

. x2y −=

2.

. 3x2xy

2

++=

3.

x

2

1y −=

.

4.

3

xy = .

5.

3

xy = .

6.

2

x

3

1

y

⎟

⎠

⎞

⎜

⎝

⎛

=

.

7.

(

)

2

x

2

logy = .

8.

. sin2yx=

9.

. 2ctgyx=+

10.

. arccosyx=

Вариант 2

Построить графики функций.

1.

1x2y

−

=

.

2.

.

2

)3x(2y −=

3.

1x

4x3

y

−

+

= .

4.

3

4

xy = .

5.

32

xy = .

6.

.

x2

3y =

7.

xlog2y

)21(

=

.

8.

(

)

2

3cos

x

y = .

9.

tg 3yx

=

.

10.

arctgyx

=

.

66

Задание 4. Многочлены

Вариант 1

1.Выполнить умножение и привести подобные члены:

).255)(5(

2

+−+ aaa

Ответ:

.125

3

+a

2. Выполнить умножение и привести подобные члены:

).23()32(3)32(5 xxxxa −

+

−−−

Ответ:

).135)(32(

−

−− xax

3. Вставить нужные числа вместо символов:

.94)3(

2

+〈〉+=+⊗ xxx

Ответ:

212

,

.⊗=± 〈〉=±

4.Разложить на множители:

.

27)12(

3

−+c

Ответ:

).13104)(1(2

2

++− ccc

5.Выделить полный квадрат:

.

2

52

2

+− xx

Ответ:

.4)1(

2

+−x

6.Произвести деление многочленов:

).1(:)22(

32

++−+− xxxxx

Ответ:

.12

2

−− xx

7.Найти значение коэффициента при

в выражении: x

).1(2)52)(32)(2(

2

−++−− xxxx

Ответ: 3.

8.Найти значение

a , при котором данное равенство верно для всех

x

:

.

3

)1(

5

1

3

7

15

3358 x

x

aa

ax

+−

⎟

⎠

⎞

⎜

⎝

⎛

+=

−−

Ответ: 0,125.

9.Найти значения

и , при которых данное равенство является верным a b

для всех

x

:

.16)17(

12

)43()43(

22

+−+−=+ xa

b

xabx

Ответ: 3; 7.

10.Найти числа

, при которых справедливо равенство:

CBA ,,

.

21)2)(1(

1

+

−

+=

+− x

C

x

B

x

A

xxx

Ответ:

.

−

6

1

;

3

1

;

2

1

67

Вигура М.А., Соболев А.Б., Рыбалко А.Ф., Рыбалко Н.М. Элементарная математика

Подождите немного. Документ загружается.