Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

550 14 Models for Tables

It is interesting that even for sparse individual tables the χ

-approximation

holds as long as the sum of row totals in all tables is larger than 20, say,

) >20.

As in contingency tables, if the marginal sums are ﬁxed in advance, the

subsequent inference does not concern the independence; it concerns the ho-

mogeneity of one factor within the levels of the other factor. The following ex-

ample tests for homogeneity of proportions of cancer incidence among smokers

and nonsmokers stratiﬁed by populations in different cities.

Example 14.10. The three 2

×2 tables provide classiﬁcation of people from

three Chinese cities, Zhengzhou, Taiyuan, and Nanchang, with respect to

smoking habits and incidence of lung cancer (Liu, 1992).

Zhengzhou Taiyuan Nanchang

Cancer Diagnosis: yes no total yes no total yes no total

Smoker 182 156 338 60 99 159 104 89 193

Nonsmoker 72 98

170 11 43 54 21 36 57

Total 254 254 508 71 142 213 125 125 250

We can apply the Mantel–Haenszel test to decide if the proportions of can-

cer incidence for smokers and nonsmokers coincide for the three cities, i.e.,

: p

= p

, where p

is the proportion of incidence of cancer among smok-

ers in city i and p

is the proportion of incidence of cancer among nonsmokers

in city i, i

= 1,2,3. We use the two-sided alternative, H

: p

6= p

, for some

∈{1,2,3} and ﬁx the type I error rate at α =0.10.

To compute

in (14.5), we ﬁnd A, E, and V . From the tables, A =

182+60+104 =346. Also, E =

=338·254/508+ 159·71/213+193·125/250 =

169 +53 +96.5 =318.5.

i=1

)(c

)(a

)(b

)

−1)

338 ·254 ·170 ·254

508

·507

159 ·71 ·54 ·142

213

·212

193 ·125 ·57 ·125

250

·249

= 28.33333 +9 +11.04518 =48.37851.

Therefore,

(|346 −318.5|−0.5)

48.37851

=15.0687.

Because the statistic

is distributed approximately as χ

, the p-value (via

MATLAB m-ﬁle

mantelhaenszel.m) is 0.0001.

[chi2, pval] = mantelhaenszel([182 156; 72 98; ...

60 99; 11 43; 104 89; 21 36])

14.5 Multiple Tables: Mantel–Haenszel Test 551

%chi2 = 15.0687

%pval = 1.0367e-004

In this case, there is clear evidence that the cancer rates are not homogeneous

among the three cities.

14.5.2 Conditional Odds Ratio

Measures of association in a 2 ×2 table have been discussed in “risk” sum-

maries: risk ratio and odds ratio (Chap. 10) are examples. Suppose that k

independent classiﬁcations into a 2

×2 table are observed.

Let the rows in the ith table

Presence Absence

Group 1 a

Group 2 c

represent Groups 1 and 2 and the columns Presence/Absence of a particular

attribute. For example, Groups could be case and control subjects and Pres-

ence/Absence can be related to a particular risk factor. The tables can be strat-

iﬁed to control for some other risk factor or demographic feature of the subjects

such as gender, age, smoking status, etc.

Then the proportion of subjects with the attribute present for Group 1

is a

/(a

), and the proportion of subjects with the attribute present for

Group 2 is c

/(c

The observed odds ratio (between the groups) for a single ith table is

The combined odds ratio for all k strata tables is deﬁned as

The expression

was proposed in Mantel and Haenszel (1959) and repre-

sents the weighted average of individual odds ratios

with weights b

An approximation to the variance of the log odds ratio

is given by

the RGB formula (Robins et al., 1986):

552 14 Models for Tables

Var (log(

OR)) =

2RS

where P

= (a

)/n

, Q

= (b

)/n

, R

= a

, S

= b

, R =

and S

. If k is equal to 1, the RGB variance formula reduces to the

familiar (

), (p. 383).

The (1

−α)100% conﬁdence interval for OR is

· exp{−z

1−α/2

σ},

· exp{z

1−α/2

σ}

where

σ =

Var (log(

OR)).

(a) (b) (c)

Fig. 14.3 (a) Nathan Mantel (1919–2002), (b) William Haenszel (1910–1998), and (c) Quinn

McNemar (1900–1986).

14.6 Paired Tables: McNemar’s Test

Another type of table commonly used in dental, opthalmology, and pharmacol-

ogy trials is matched-pair tables summarizing the designs in which interven-

tions are applied to the same patient. For example, in randomized split-mouth

trials comparing the effectiveness of tooth-speciﬁc interventions to prevent de-

cay, one tooth in a subject is randomly selected to receive treatment A while

the contralateral tooth in the same subject receives treatment B. Another ex-

ample is crossover trials testing the efﬁcacy of drugs. In this design, a patient

is randomly administered treatment A or B in the ﬁrst time period and then

administered the remaining treatment in the second time period. The link

between the split-mouth design and crossover trials is apparent – the tooth

location in the split-mouth design is analogous to time in the crossover design.

The matched-pair design has statistical advantages. Because the control

and test groups are subject to the same environment, this design controls for

many confounding factors. Thus differences in outcomes between test and con-

14.6 Paired Tables: McNemar’s Test 553

trol groups are likely attributable to the treatment. Moreover, since control

and test groups receive both interventions, matched-pair studies usually re-

quire no more than half the number of subjects to produce the same precision

as parallel group studies.

McNemar’s test (after Quinn McNemar, Fig.14.3c) used for inference in

paired tables. Although data for the McNemar test resemble contingency ta-

bles, the structure of the tables is quite different and the inference is quite

different. For simplicity, assume that measurements at Before and After on

the same subject result in Positive and Negative responses. From N subjects

we obtain 2N responses, or N pairs of responses, organized as follows:

After

Positive Negative Total

Before

Positive

A B A +B

Negative

C D C +D

Total A +C B +D N

For example, A is the number of subjects (pairs of responses) where both

Before and After resulted in a positive. More generally, Before and After could

be any two different groups of matched subjects that produce binary responses.

The marginal sum A

+B is the number of positives in Before and A +C is

the number of positives in After. The proportion of positives in Before is

A+B

, while the proportion of positives in After is

A+C

. Let the population

counterparts of

and

be p

and p

14.6.1 Risk Differences

The McNemar test examines the difference between the proportions that de-

rive from the marginal sums and tries to infer if the two population propor-

tions p

and p

differ signiﬁcantly. The difference between this test and the

test for two proportions from Chap. 10, p. 381, is that in the paired tables

the two proportions are not independent. Note that both sample proportions

depend on A from the upper left cell of the table. The inference about the dif-

ference between p

and p

involves only entries B and C from the table, since

A/N cancels.

Under the hypothesis H

: p

= p

, both B and C are distributed as bino-

mial

B in(B +C,0.5). In this case, EB =

B+C

and Var (B) =

B+C

. By the CLT,

B −EB

Var (B)

B −(B +C)/2

B +C

Thus, after simplifying and squaring, we obtain the statistic

554 14 Models for Tables

= Z

(B −C)

B +C

which has an approximately

-distribution with 1 degree of freedom. Large

values of

are critical.

When B

+C is small, it is recommended to use a continuity correction in χ

as χ

= Z

(|B−C|−1)

B+C

The conﬁdence interval for the difference in proportions is

[

−

−z

1−α/2

−

1−α/2

]

where s is the square root of s

, and

(1 −

)

(1 −

)

−

)

where

= A/N,

= B/N,

= C/N, and

= D/N. Note that the ﬁrst

two factors in the expression for s

are for the case of independent proportions,

while the third factor accounts for the dependence.

14.6.2 Risk Ratios

The risk ratio is deﬁned as

RR =

A +B

A +C

with variance for the log(RR),

Var (log(RR) =

A +B

A +C

−

(A +B)(A +C)

14.6.3 Odds Ratios

To conduct the inference on odds ratios in paired tables, we use the Mantel–

Haenszel theory with parallel (unpaired) tables derived from a paired table.

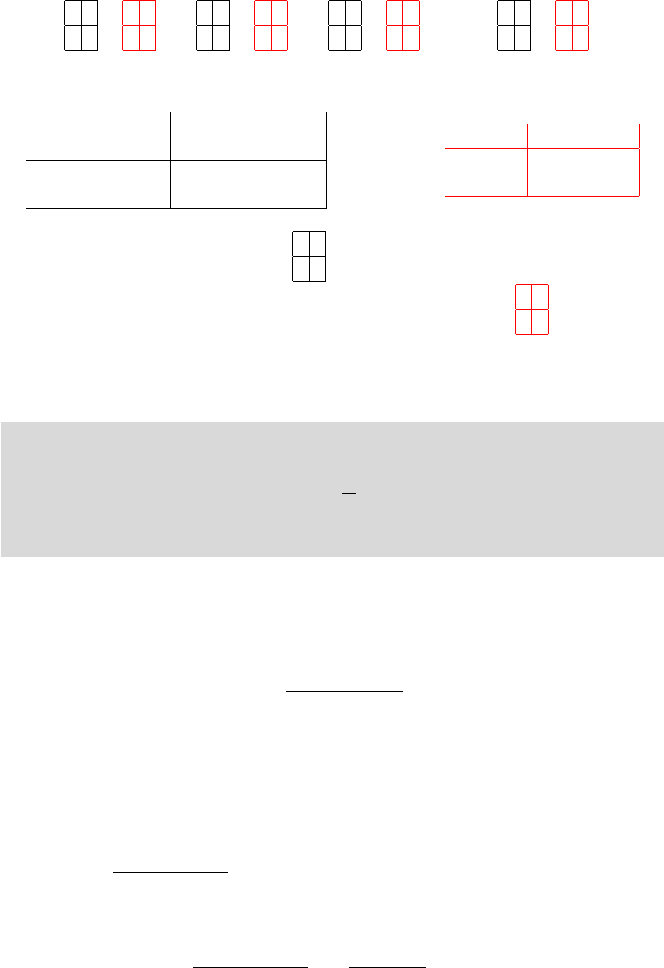
14.6 Paired Tables: McNemar’s Test 555

Any table with N paired observations generates N Mantel–Haenszel tables

1 0

0 0

7→

1 1

0 0

0 1

0 0

7→

1 0

0 1

0 0

1 0

7→

0 1

1 0

and

0 0

0 1

7→

0 0

1 1

where the ﬁrst table is paired and the second (red) is parallel.

After

Positive Negative

Before

Positive

• •

Negative • •

−→

Before After

Positive • •

Negative • •

For example, 1 in the paired cell

1 0

0 0

where both Before and After are Posi-

tive is translated to 1 for each Before and After in a table

1 1

0 0

, contrasting

Positives and Negatives for Before and After. From an analysis of Mantel–

Haenszel tables one can show that the empirical odds ratio for the probabili-

ties p

and p

OR =

To ﬁnd the conﬁdence interval on the log(OR) we use the Miettinen’s test-

based method (Miettinen, 1976). First note that when H

is true, McNemar’s

-statistic can be expressed as

(log(OR) −0)

Var [log(OR)]

in which the only unknown is

Var [log(OR)] since log(OR) =log(B/C) and χ

(|B −C|−1)

/(B +C) are easy to ﬁnd. By solving it for Var [log(OR)], one can

ﬁnd the conﬁdence interval for log(OR) as

[

log(OR)

−z

1−α/2

s, log(OR) + z

1−α/2

]

where s

Var [log(OR)]. Of course, the conﬁdence interval for the OR is

derived from the above using antilogs.

Another formula for variance in a matched-pairs table comes from the

Robins, Breslow, and Greenland (RGB) estimator for Mantel–Haenszel un-

matched cases, s

Var [log(OR)] =

1/B +1/C. It is easy to see that the

estimator of log(OR) is consistent since when the number of tables goes to

inﬁnity, s

→0.

556 14 Models for Tables

MATLAB function mcnemart.m computes the estimators and conﬁdence

intervals for McNemar’s layout.

function [] = mcnemart(matr)

% input matr is matrix [A B; C D]

A=matr(1,1); B= matr(1,2); C= matr(2,1); D=matr(2,2);

if( A

D==0 )

matr = matr + 0.5;

end

N = A + B + C + D;

p1 = (A + B)/N; %prob row

p2 = (A + C)/N; %prob column

p11 = A/N; p12 = B/N; p21 = C/N; p22 = D/N;

% risk difference

diffp1p2 = p1 - p2

delta = p11

p22 - p12

p21

s = sqrt( p1

(1-p1)/N + p2

(1-p2)/N + 2

delta/N )

ssel = sqrt( ((B+C)

N - (B-C)^2)/N^3 )

lbd = p1 - p2 - norminv(0.975)

ubd = p1 - p2 + norminv(0.975)

cidiff = [lbd, ubd]

% odds ratio

or1 = B/C

% miettinen approx

s2lor1 = (log(B/C))^2

(B+C)/((abs(B-C)-1)^2 + 0.0000001)

slor1 = sqrt(s2lor1)

lblor1 = log(or1) - norminv(0.975)

slor1 ;

ublor1 = log(or1) + norminv(0.975)

slor1 ;

miettlint = [lblor1, ublor1]

miettint = [exp(lblor1), exp(ublor1)]

% RGB approx

slor2 = sqrt(1/B + 1/C)

lblor2 = log(or1) - norminv(0.975)

slor2 ;

ublor2 = log(or1) + norminv(0.975)

slor2 ;

rgblint = [lblor2, ublor2]

rgbint = [exp(lblor2), exp(ublor2)]

% --------- exact method ------------------

df1l = 2

C +2; df2l = 2

F1 = finv(0.975, df1l, df2l);

tl = B/(B+(C+1)

F1 );

orexactl = tl/(1-tl);

df1u = 2

B +2; df2u = 2

F2 = finv(0.975, df1u, df2u);

tu = (B+1)

F2/(C+(B+1)

F2 );

14.6 Paired Tables: McNemar’s Test 557

orexactu = tu/(1-tu);

exactorci = [orexactl, orexactu]

%--------- approximate prob ---------

phat = B/(B+C);

pl = phat - norminv(0.975)

sqrt(phat

(1-phat)/(B+C)) - 1/(2

B+2

C);

pu = phat + norminv(0.975)

sqrt(phat

(1-phat)/(B+C)) + 1/(2

B+2

C);

intor = [pl/(1-pl), pu/(1-pu)]

Example 14.11. Split-Mouth Trials for Dental Sealants. Randomized split-

mouth trials (RSM) are frequently used in dentistry to examine the effective-

ness of preventive interventions that impact individual teeth as opposed to the

whole mouth. For example, to examine the effectiveness of dental sealants in

preventing caries, a permanent ﬁrst molar is randomly chosen for the inter-

vention while its contralateral tooth serves as the control. Because the control

and test teeth are subject to the same oral environment, this design controls

for many confounding factors such as diet, tooth morphology, and oral hygiene

habits. Thus differences in outcomes between test and control teeth are likely

attributable to the treatment. Because of this pairing, adequate power may be

achieved with a smaller sample size than if the teeth were independent.

Forss and Halme (1998) report results of a split-mouth study that started

in 1988 with 166 children, with the goal of assessing tooth-sealant materials.

Participants were children from Finland, aged 5 to 14 years (mean age 11

years). To be included in the study, children had to have a contralateral pair

of newly erupted, sound, unsealed permanent ﬁrst or second molar teeth.

Interventions on the occlusal surfaces of sound ﬁrst or second permanent

molars involved glass ionomer Fuji III sealant as a treatment and third-

generation, resin-based, light-cured Delton sealant as control. The results are

recorded at the 7-year follow-up involving 97 children (the dropout rate was

42%).

Control (Resin)

Caries No Caries Total

Treatment (Fuji III)

Caries

8 15 23

No Caries

8 66 74

Total 16 81 97

Risk differences and risk and odds ratios with conﬁdence intervals are ob-

tained by the MATLAB program

mcnemart.m. Several approaches to con-

ﬁdence intervals (exact, approximate RGB, approximate Miettinen) are pre-

sented. The odds ratio is 1.8750, the exact 95% conﬁdence interval for OR is

[0.7462, 5.1064], and three approximations are

miettint = [0.7003, 5.0198],

rgbint = [0.7950, 4.4224], and intor = [0.7724, 6.6080].

The complete output from

mcnemart.m is

mcnemart([8, 15; 8, 66])

%diffp1p2 = 0.0722

558 14 Models for Tables

%delta = 0.0434

%s = 0.0646

%ssel = 0.0489

%cidiff = -0.0545 0.1989

%or1 = 1.8750

%s2lor1 = 0.2525

%slor1 = 0.5025

%miettlint = -0.3562 1.6134

%miettint = 0.7003 5.0198

%slor2 = 0.4378

%rgblint = -0.2295 1.4867

%exactorci = 0.7462 5.1064

%intor = 0.7724 6.6080

Example 14.12. Schistosoma Mansoni. Schistosoma mansoni is a parasite

that is found in Africa, Madagascar, parts of South America (such as Venezuela

and Brazil), Puerto Rico, and the West Indies. Among human parasitic dis-

eases, schistosomiasis ranks second behind malaria in terms of socioeconomic

and public health importance in tropical and subtropical areas. Some estimate

that there are approx. 20,000 deaths related to schistosomiasis yearly. Sleigh

et al. (1982) compare results of one Bell and one Kato-Katz examination per-

formed on each of 315 stool specimens from residents in an area in northeast-

ern Brazil endemic for schistosomiasis mansoni. The following table, discussed

also in Kirkwood and Sterne (2003), summarizes the ﬁndings.

Kato-Katz Positive Kato-Katz Negative Total

Bell Positive 184 54 238

Bell Negative 14 63 77

Total 198 117 315

Is the probability of detecting Schistosomiasis mansoni the same for the

two tests? Find the odds ratio and its approximate conﬁdence intervals. From

the output of

mcnemart.m we have

%or1 = 3.8571

%miettint = 2.2045 6.7488

%exactorci = 2.1130 7.5193

%intor = 2.2327 8.7633

Example 14.13. Testing for Salmonella. Large discrepancies are usually

found when different ELISAs for the diagnosis of pig salmonellosis are com-

pared. Mainar-Jaime et al. (2008) explored the diagnostic agreement of two

commercial assays: (i) Salmonella Covalent Mix-ELISA (Svanovir), positive

OD% =20% denoted as test A and (b) Swine Salmonella Antibody Test Kit

(HerdCheck), positive OD% =10% as test B, for the detection of antibodies to

Salmonella spp. in slaughter pigs.

14.6 Paired Tables: McNemar’s Test 559

Populations of pigs slaughtered in abattoirs from Saskatchewan, Canada.

Population 1: animals from farms marketing

<10,000 pigs/year.

Population 2: animals from farms marketing 10,000 pigs/year.

Population 1 Population 2

Test B + Test B – Total Test B + Test B – Total

Test A + 11 16 27 2 5 7

Test A – 6 119

125 1 72 73

Total 17 135 152 3 77 80

From McNemar’s χ

-test one concludes that test A (at either OD% = 40%

or OD% =20%) signiﬁcantly differs from test B in the proportion positive at

α =0.05.

14.6.4 Multicategorical Paired Tables: Stuart–Maxwell

Test*

A natural generalization of the McNemar test is a design in which there are N

matched pairs where each response can be classiﬁed into k

>2 different cate-

gories. We will be interested in the equality of proportions for categories in the

two populations that form the paired responses. For simplicity we discuss only

the case of k

= 3. A general test is given in Maxwell (1970) and implemented

as MATLAB function

stuartmaxwell.m.

Assume that paired responses come from Before and After and each re-

sponse may result in one of the three categories: Positive, Neutral, and Nega-

tive.

After

Positive Neutral Negative Total

Positive n

1·

Before Neutral n

2·

Negative n

3·

Total n

·1

·2

·3

Notice that the table counts matched pairs, for example, n

is the number

of cases where Before resulted in neutral and After resulted in negative. Thus,

again we have a total of 2N responses organized into N matched pairs.

Denote by p

i j

the population proportion of subjects in population i (one of

Before, After) that are classiﬁed as j (one of Positive, Neutral, or Negative).

The null hypothesis of interest is

: p

= p

, p

= p

, and p

= p