Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

510 13 Goodness-of-Fit Tests

No. of dice resulting in Observed

or when 12 dice are rolled frequency

0 185

1 1149

2 3265

3 5475

4 6114

5 5194

6 3067

7 1331

8 403

9 105

10 14

11 4

12 0

In Pearson (1900), the value of χ

-statistic was quoted as 43.9, which is

slightly different than the correct value. The discrepancy is probably due to

the use of expected frequencies rounded to the nearest integer and due to the

accumulation of rounding errors when calculating

To ﬁnd the expected frequencies, recall the binomial distribution. The num-

ber of times

or was rolled with 12 dice is binomial: B in(12, 1/3). To ﬁnd

the expected frequencies, multiply the total number of rolls 26,306 by the ex-

pected (theoretical) probabilities obtained from

B in(12,1/3), as in the follow-

ing MATLAB output:

obsfreq = [ 185 1149 3265 5475 6114 5194 ...

3067 1331 403 105 14 4 0];

n = sum(obsfreq) %26306

expected = n

binopdf(0:12, 12, 1/3)

%expected =

% 1.0e+003

% 0.2027 1.2165 3.3454 5.5756 6.2726 5.0180 2.9272

% 1.2545 0.3920 0.0871 0.0131 0.0012 0.0000

chisqs = (obsfreq - expected).^2./expected

%chisqs =

% 1.5539 3.7450 1.9306 1.8155 4.0082 6.1695 6.6772

% 4.6635 0.3067 3.6701 0.0665 6.6562 0.0495

chi2 = sum(chisqs)

%chi2 = 41.3122

pval=1 - chi2cdf(chi2, 13-1)

% pval = 4.3449e-005

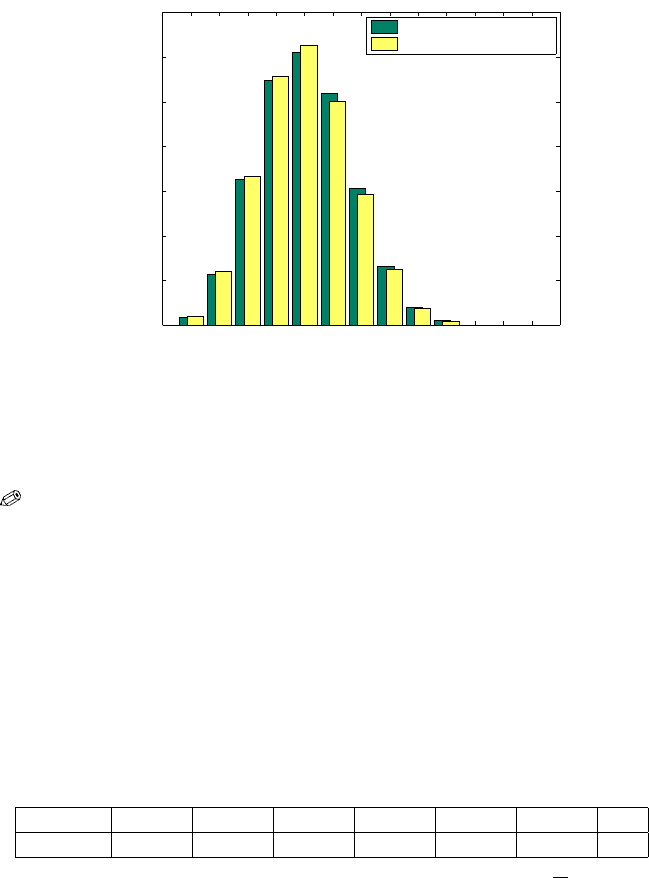
13.3 Pearson’s Chi-Square Test 511

crit = chi2inv(0.95, 13-1)

% crit = 21.0261

As evident from the MATLAB output, the observations are not supporting

the fact that the dice were fair (p-value of 4.3449e-05), see also Fig. 13.5.

1 2 3 4 5 6 7 8 9 10 11 12 13

1000

2000

3000

4000

5000

6000

7000

Number of 5s, 6s out of 12 rolls

Frequency

Observed Frequencies

Theoretical Frequencies

Fig. 13.5 Bar plot of observed frequencies and theoretical frequencies. Although the graphs

appear close, the large sample size makes the discrepancy of this size very unlikely. It is

almost certain that one or more of Weldon’s 12 dice were not well balanced.

Example 13.4. Is the Process Poisson? The Poisson process is one of the

most important stochastic models. For example, random arrival times of pa-

tients to a clinic are well modeled by a Poisson process. This means that in any

interval of time, say [0, t], the number of arrivals is Poisson with parameter

λt. For such Poisson processes, the interarrival times follow an exponential

distribution with density f (t)

= λe

−λt

, t ≥ 0,λ > 0. It is often of interest to

establish the Poissonity of a process since many theoretical results are avail-

able for such processes, which are ubiquitous in queueing theory and various

engineering applications.

The interarrival times of the arrival process were recorded, and it was

observed that n

=109 recorded times could be categorized as follows:

Interval 0 ≤ T <1 1 ≤T <2 2 ≤ T <3 3 ≤ T <4 4 ≤ T <5 5 ≤ T <6 T ≥6

Frequency 34 20 16 15 9 7 8

A simple calculation determined that the sample mean was T = 5/2. Test

the hypothesis that the process described with the above interarrival times is

Poisson, at level

α =0.05.

512 13 Goodness-of-Fit Tests

Given this data, one should test the hypothesis that the interarrivals times

are exponential. The density f (t)

= λe

−λt

, t ≥0,λ > 0 corresponds to the CDF

F(t)

=1 −e

−λt

, t ≥ 0, λ > 0, and the theoretical probability of an interval [a, b]

is F(b)

−F(a).

But we ﬁrst need to estimate the parameter

λ in order to calculate the

(theoretical) probabilities. A standard estimator for the parameter

λ is

λ =

1/T =1/(5/2) =0.4.

The theoretical frequencies of intervals [3,4] and [4,5] are p

=109·(F(4)−

F(3)) = 109 ·(1 − e

−0.4·4

−(1 −e

−0.4·3

)) = 109 ·(e

−0.4·3

−e

−0.4·3

) = 0.099298 ·109 =

10.823 and 0.066561 ·109 =7.255, respectively, yielding χ

equal to

(34

−35.9335)

35.935

(20 −24.089)

24.089

(16 −16.147)

16.147

(15 −10.823)

10.823

(9 −7.255)

7.255

(7 −4.863)

4.863

(8 −9.888)

9.888

=4.13.

The number of degrees of freedom is d f

=7−1−1 =5 and the 95% quantile

for

is chi2inv(0.95,5)=11.071. Thus, we do not reject the hypothesis that

the interarrival times are exponential, i.e., the observed process is consistent

with a Poisson process.

Example 13.5. A sample of n=1000 exponential E (1/2) random variates is gen-

erated. We pretend that the generating distribution is unknown. Using MAT-

LAB’s

chi2gof function we test the consistency of the generated data with an

exponential distribution with the rate

λ estimated from the sample.

X = exprnd(2, [1, 1000]);

[h,p,stats] = ...

chi2gof(X,’cdf’,@(z)expcdf(z,mean(X)),’nparams’,1,’nbins’,7)

%h = 0

%p = 0.6220

%stats = chi2stat: 2.6271

% df: 4

% edges: [1x7 double]

% O: [590 258 96 34 14 8]

% E: [1x6 double]

The sample is consistent with the exponential distribution with p-value of

0.6220. Note that the number of intervals selected by MATLAB is 6, not the

requested 7. This is because the upper tail intervals with a low expected count

(

<5) are merged.

Example 13.6. Wrinkled Peas. Mendel crossed peas that were heterozygotes

for smooth/wrinkled, where smooth is dominant. The expected ratio in the off-

spring is 3 smooth: 1 wrinkled. He observed 423 smooth and 133 wrinkled

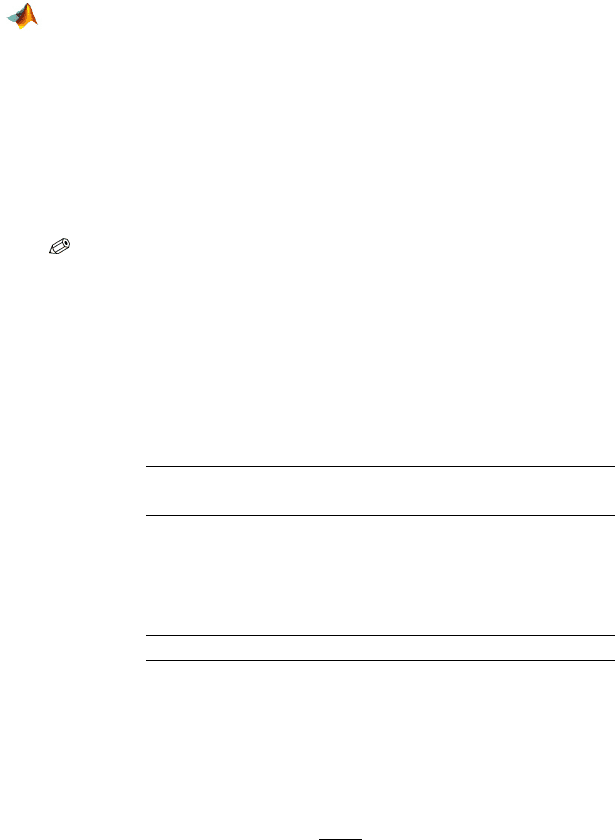
13.3 Pearson’s Chi-Square Test 513

peas. The expected frequency of smooth is calculated by multiplying the sam-

ple size (556) by the expected proportion (3/4) to yield 417. The same is done

for wrinkled to yield 139. The number of degrees of freedom when an extrin-

sic hypothesis is used is the number of values of the nominal variable minus

one. In this case, there are two values (smooth and wrinkled), so there is one

degree of freedom.

chisq = (556/4 - 133)^2/(556/4) + (556

3/4 - 423)^2/(556

3/4)

%chisq = 0.3453

1 - chi2cdf(chisq, 2-1)

%ans = 0.5568

chisqy = (abs(556/4 - 133)-0.5)^2/(556/4) + ...

(abs(556

3/4 - 423)-0.5)^2/(556

3/4) %with Yates correction

%chisq = 0.2902

1-chi2cdf(chisqy, 2-1)

%ans = 0.5901

We conclude that the theoretical odds 3:1 in favor of smooth peas are con-

sistent with the observations at level

α =0.05.

Example 13.7. Horse-Kick Fatalities. During the latter part of the nine-

teenth century, Prussian ofﬁcials gathered information on the hazards that

horses posed to cavalry soldiers. Fatal accidents for 10 cavalry corps were col-

lected over a period of 20 years (Preussischen Statistik). The number of fatali-

ties due to kicks, x, was recorded for each year and each corps. The table below

shows the distribution of x for these 200 “corps-years.”

Observed number of corps-years

x = number of deaths in which x fatalities occurred

0 109

1 65

2 22

3 3

≥4 1

200

Altogether there were 122 fatalities [109(0) +65(1) +22(2) +3(3) +1(4)],

meaning that the observed fatality rate was 122/200, or 0.61 fatalities per

corps-year. Von Bortkiewicz (1898) proposed a Poisson model for X with a

mean of c = 0.61. The table below shows the observed and expected frequencies

corresponding to x

= 0,1,2,. . ., etc. The expected frequencies are

0.61

exp

{−0.61},

for n

= 200 and i = 0,1,2, and 3. We put together all values ≥ 4 as a single

class; this will ensure that the sum of the theoretical probabilities is equal to

1. For example, the expected frequencies np

are

514 13 Goodness-of-Fit Tests

npi = 200

[poisspdf(0:3, 0.61) 1-poisscdf(3, 0.61)]

%npi = 108.6702 66.2888 20.2181 4.1110 0.7119

0 0.5 1 1.5 2 2.5 3

−2.2

−2

−1.8

−1.6

−1.4

−1.2

−1

−0.8

−0.6

log(n

) + log(i!) − log(N)

Fig. 13.6 Poissonness plot for von Bortkiewicz’s data. The theoretical line, log(0.61)i −0.61,

is shown in red.

Observed number of Expected number of

i # of fatalities corps-years, n

corps-years, e

1 0 109 108.6702

2 1 65 66.2888

3 2 22 20.2181

4 3 3 4.1110

≥4 1 0.7119

200 200

Now we calculate the statistic χ

−n p

)

/(np

) and ﬁnd the p-

value for the test and rejection region. Note that the number of degrees of

freedom is df

=5 −1 −1 since λ =0.61 was estimated from the data.

ni = [109 65 22 3 1]

% ni = 109 65 22 3 1

ch2 = sum( (ni-npi).^2 ./npi )

% ch2 = 0.5999

1-chi2cdf(0.5999, 5-1-1)

% ans = 0.8965, pvalue

chi2inv(0.95, 5-1-1)

% ans = 7.8147, critical value

% rejection region [7.8147, infinity)

13.4 Kolmogorov–Smirnov Tests 515

The Poisson distribution in H

is consistent with the data at the level α =

0.05. Clearly the agreement between the observed and expected frequencies is

remarkable, see also Poissonness plot in Fig. 13.6.

13.4 Kolmogorov–Smirnov Tests

The ﬁrst measure of goodness of ﬁt for general distributions was derived by

Kolmogorov (1933). Andrei Nikolaevich Kolmogorov (Fig. 13.7a), the most ac-

complished and celebrated Russian mathematician of all time, made funda-

mental contributions to probability theory, including a test statistic for dis-

tribution functions, some of which are named after him. Nikolai Vasilyevich

Smirnov (Fig. 13.7b), another Russian mathematician, extended Kolmogorov’s

results to two samples.

(a) (b)

Fig. 13.7 (a) Andrei Nikolaevich Kolmogorov (1905–1987); (b) Nikolai Vasilyevich Smirnov

(1900–1966).

13.4.1 Kolmogorov’s Test

Let X

, X

,... , X

be a sample from a population with a continuous, but

unknown, CDF F. As in (2.2), let F

(x) be the empirical CDF based on

, X

,... , X

We are interested in testing the hypothesis

: F(x) =F

(x), (∀x) versus H

: F(x) 6=F

(x), (∃x),

where F

(x) is a fully speciﬁed continuous distribution.

The test statistic D

is calculated from the sample as

516 13 Goodness-of-Fit Tests

= max

1≤i≤n

−F

), F

) −

i −1

When hypothesis H

is true, Kolmogorov (1933) showed that the statistic

is approximately distributed as

lim

n→∞

≤ x) =K(x) =1 −2

∞

k=1

(−1)

k−1

−2k

, x ≥0,

which allows one to calculate critical regions and p-values for this test.

The MATLAB ﬁle

kscdf.m calculates the CDF K. Since large values of

are critical for H

, the p-value of the test is approximated as

p ≈1 −K(

or in MATLAB as

1-kscdf(sqrt(n)

Dn).

In practice, most KS-type tests are two-sided, testing whether F is equal

to F

, the distribution postulated by H

, or not. Alternatively, one might test

to see if the distribution is larger or smaller than a hypothesized F

[see, for

example, Kvam and Vidakovic (2007)].

Example 13.8. To illustrate the Kolmogorov test we simulate 30 observations

from an exponential distribution with

λ =1/2.

% rand(’state’, 0);

% n = 30; i = 1:n;

% x = exprnd(1/2,[1,n]); x = sort(x);

x = [...

0.0256 0.0334 0.0407 0.0434 0.0562 0.0575...

0.0984 0.1034 0.1166 0.1358 0.1518 0.2427...

0.2497 0.2523 0.3608 0.3921 0.4052 0.4455...

0.4511 0.5208 0.6506 0.7324 0.7979 0.8077...

0.8079 0.8679 0.9870 1.4246 1.9949 2.309];

distances = [i./n - expcdf(x, 1/2); expcdf(x, 1/2) - (i-1)./n ];

Dn = max(max(distances)) %0.1048

pval = 1 - kscdf(sqrt(n)

Dn) %0.8966

The p-value is 0.8966 and H

is not rejected. In other words, the sample

is consistent with the hypothesis of the population’s exponential distribution

E (1/2).

13.4 Kolmogorov–Smirnov Tests 517

The CDF K (x) is an approximate distribution for

and for small val-

ues of n may not be precise. Better approximations use a continuity correction:

≈1 −K

This approximation is satisfactory for n

≥20.

1 - kscdf(sqrt(n)

Dn + 1/(6

sqrt(n)) ) %0.8582

MATLAB has a built-in function, kstest, that produces similar output.

% form theoretical cdf

t = 0:0.01:20;

y = expcdf(t,1/2);

cdf = [t’ y’];

[decision, pval, KSstat, critValue] = kstest(x, cdf, 0.01, 0)

%decision = 0

%pval = 0.8626

%KSstat = 0.1048

%critValue = 0.2899

Figure 13.8 shows the empirical and theoretical distribution in this exam-

ple and it is produced by the code below.

%Plot

xx = 0:0.01:4;

plo = cdfplot(x); set(plo,’LineWidth’,2);

hold on

plot(xx,expcdf(xx, 1/2),’r-’,’LineWidth’,2);

legend(’Empirical’,’Theoretical Exponential’,...

’Location’,’SE’)

Note that in the two calculations the values of D

statistics coincide but

the p-values differ. This is because

kstest uses a different approximation to

the p-value.

The Kolmogorov test has advantages over exact tests based on the χ

goodness-of-ﬁt statistic, which depend on an adequate sample size and proper

interval assignments for the approximations to be valid. A shortcoming of the

KS test is that the F

distribution in H

must be fully speciﬁed. That is, if

location, scale, or shape parameters are estimated from the data, the criti-

cal region of the KS test is no longer valid. An example is Lilliefors’ test for

departures from normality when the null distribution is not fully speciﬁed.

13.4.2 Smirnov’s Test to Compare Two Distributions

Smirnov (1939) extended the Kolmogorov test to compare two distributions

based on independent samples from each population. Let X

, X

,... , X

and

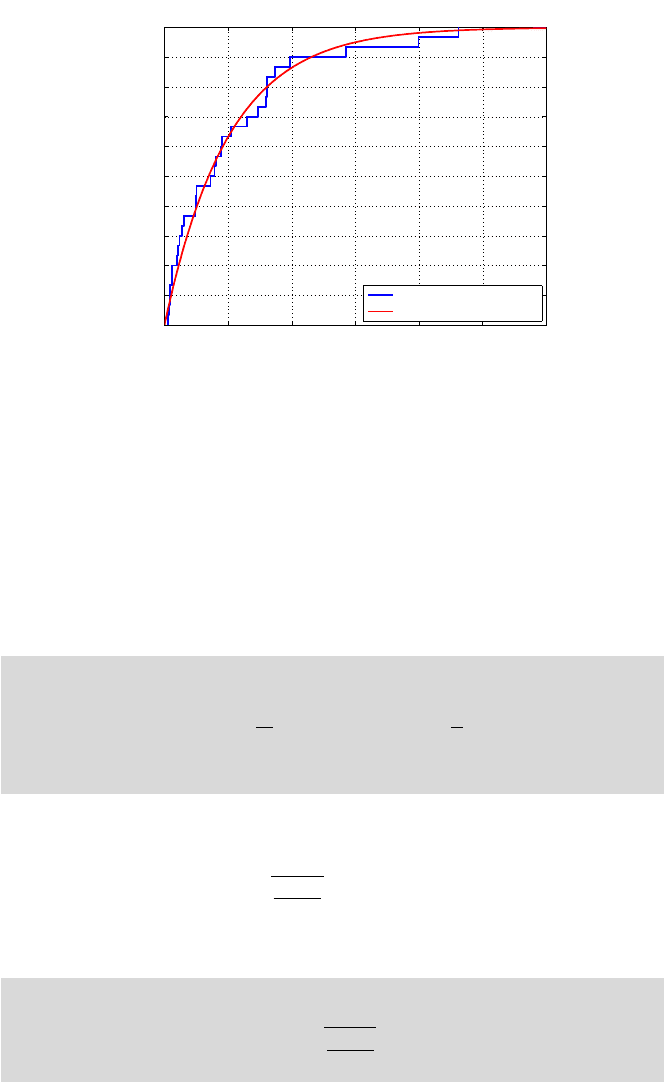
518 13 Goodness-of-Fit Tests

0 0.5 1 1.5 2 2.5 3

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

F(x)

Empirical CDF

Empirical

Theoretical Exponential

Fig. 13.8 Empirical and theoretical distributions in the simulated example.

,... , Y

be two independent samples from populations with unknown

CDFs F

and G

. Let F

(x) and G

(x) be the corresponding empirical dis-

tribution functions.

We would like to test

: F

(x) =G

(x) ∀x versus H

: F

(x) 6=G

(x) for some x.

We will use the analog of the Kolmogorov statistic

m,n

=max

max

1≤i≤m

−G

)

, max

1≤j≤n

−F

)

¾¾

The limiting distribution for D

m,n

can be expressed by Kolmogorov’s CDF

K as

lim

→∞

m +n

m,n

≤ x

K(x),

and the p-value for the test is approximated as

p ≈1 −K

m +n

m,n

. (13.3)

13.4 Kolmogorov–Smirnov Tests 519

This approximation is good when both m and n are large.

Remark. The approximation of the p-value in (13.3) can be improved by

continuity corrections as

≈1 −K

m +n

m,n

m −n|

6mn

m,n

¶¶

where

m,n

(m +n) (min(m, n)−gcd(m, n))

2mn(m +n +gcd(m, n))

and gcd(m, n) is the greatest common divisor of m and n. This approximation

is satisfactory if m, n

>20.

If m

= n are not large, then exact p-values can be found by using ranks and

combinatorial calculations.

Example 13.9. To illustrate Smirnov’s test we simulate m

= 39 observations

from a normal

N (−1,2

) distribution and n = 35 observations from Student’s

t-distribution with 10 degrees of freedom. The hypothesis of equality of distri-

butions is rejected at the level

α = 0.05 since the p-values are approximately

in the neighborhood of 2%.

Notice that the corrected p-value 0.0196 is close to that in

kstest2, and the

differences are due to different approximation formulas.

x =[...

-5.75 -3.89 -3.69 -3.68 -3.54 -2.59 ...

-2.53 -2.40 -2.39 -2.27 -2.02 -1.72 ...

-1.64 -1.54 -1.27 -1.11 -1.08 -1.00 ...

-0.88 -0.84 -0.47 -0.36 -0.29 -0.24 ...

-0.20 -0.19 0.02 0.15 0.25 0.45 ...

0.51 0.72 0.74 0.96 1.25 1.33 ...

1.49 2.39 2.59 ];

y=[...

-2.72 -2.18 -1.31 -1.17 -1.00 -0.94 ...

-0.78 -0.65 -0.63 -0.52 -0.40 -0.37 ...

-0.30 -0.21 -0.19 -0.11 -0.05 0.12 ...

0.14 0.25 0.27 0.35 0.45 0.48 ...

0.48 0.60 0.71 0.76 0.79 1.01 ...

1.10 1.10 1.12 1.36 2.03 ];

m = length(x); n=length(y);

i = 1:m; j = 1:n;

distances = [i./m - empiricalcdf(x, y), j./n - empiricalcdf(y, x)];

Dmn = max(max(distances)) %0.3414

z = sqrt(m

n/(m + n))

Dmn %1.4662

pval1 = 1 - kscdf(z) %0.0271

bmn = (m+n)/(2

(min(m,n) - gcd(m, n))/(m + n + gcd(m,n)) %0.0123

zz = sqrt(m

n/(m + n))

(Dmn + abs(m-n)/(6

n) + bmn ) %1.5211