Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

Chapter References 277

Miller, E. G. (1991). Asymptotic test statistics for coefﬁcient of variation. Comm. Stat. Theory

Methods, 20, 10, 3351–3363.

Pritz, M. B., Zhou, X. H., and Brizendine, E. J. (1996). Hyperdynamic therapy for cerebral

vasospasm: a meta-analysis of 14 studies. J. Neurovasc. Dis., 1, 6–8.

Rutherford, E., Chadwick, J., Ellis, C. D. (1930). Radiations from Radioactive Substances.

Macmillan, London, pp. 171–172.

Rutherford, E. and Geiger, H. (1910). The probability variations in the distribution of

α-

particles (with a note by H. Bateman). Philos. Mag., 6, 20, 697–707.

Sampford, M. R. and Taylor, J. (1959). Censored observations in randomized block experi-

ments. J. Roy. Stat. Soc. Ser. B, 21, 214–237.

Staudte, R. G. and Sheater, S. J. (1990). Robust Estimation and Testing, Wiley, New York.

Wald, A. and Wolfowitz, J. (1939). Conﬁdence limits for continuous distribution functions.

Ann. Math. Stat., 10, 105–118.

Wilcox, R. R. (2005). Introduction to Robust Estimation and Hypothesis Testing, 2nd edn.

Academic, San Diego.

Wilson, E. B. (1927). Probable inference, the law of succession, and statistical inference. J.

Am. Stat. Assoc., 22, 209–212.

Chapter 8

Bayesian Approach to Inference

Bayesian: Breeding a statistician with a clergyman to produce the much sought honest

statistician.

– Anonymous

WHAT IS COVERED IN THIS CHAPTER

• Bayesian Paradigm

• Likelihood, Prior, Marginal, Posterior, Predictive Distributions

• Conjugate Priors. Prior Elicitation

• Bayesian Computation

• Estimation, Credible Sets, Testing, Bayes Factor, Prediction

8.1 Introduction

Several paradigms provide a basis for statistical inference; the two most dom-

inant are the frequentist (sometimes called classical, traditional, or Neyman–

Pearsonian) and Bayesian. The term Bayesian refers to Reverend Thomas

Bayes (Fig. 8.1), a nonconformist minister interested in mathematics whose

posthumously published essay (Bayes, 1763) is fundamental for this kind of

inference. According to the Bayesian paradigm, the unobservable parameters

in a statistical model are treated as random. Before data are collected, a prior

B. Vidakovic, Statistics for Bioengineering Sciences: With MATLAB and WinBUGS Support, 279

Springer Texts in Statistics, DOI 10.1007/978-1-4614-0394-4_8,

280 8 Bayesian Approach to Inference

distribution is elicited to quantify our knowledge about the parameter. This

knowledge comes from expert opinion, theoretical considerations, or previous

similar experiments. When data are available, the prior distribution is up-

dated to the posterior distribution. This is a conditional distribution that in-

corporates the observed data. The transition from the prior to the posterior is

possible via Bayes’ theorem.

The Bayesian approach is relatively modern in statistics; it became inﬂu-

ential with advances in Bayesian computational methods in the 1980s and

1990s.

Fig. 8.1 The Reverend Thomas Bayes (1702–1761), nonconformist priest and mathemati-

cian. His Essay Towards Solving a Problem in the Doctrine of Chances, presented to the

Royal Society after his death, contains a special case of what is now known as Bayes’ theo-

rem.

Before launching into a formal exposition of Bayes’ theorem, we revisit

Bayes’ rule for events (p. 86). Prior to observing whether an event A has ap-

peared or not, we set the probabilities of n hypotheses, H

, H

,... , H

, un-

der which event A may appear. We called them prior probabilities of the hy-

potheses,

P(H

),... , P(H

). Bayes’ rule showed us how to update these prior

probabilities to the posterior probabilities once we obtained information about

event A. Recall that the posterior probability of the hypothesis H

, given the

evidence about A, was

P(H

|A) =

(A|H

)P(H

)

P(A)

Therefore, Bayes’ rule gives a recipe for updating the prior probabilities of

events to their posterior probabilities once additional information from the ex-

periment becomes available. The focus of this chapter is on how to update prior

8.1 Introduction 281

knowledge about a model; however, this knowledge (or lack of it) is expressed

in terms of probability distributions rather than by events.

Suppose that before the data are observed, a description of the population

parameter

θ is given by a probability density π(θ). The process of specifying

the prior distribution is called prior elicitation. The data are modeled via the

likelihood, which depends on

θ and is denoted by f (x|θ). Bayes’ theorem up-

dates the prior

π(θ) to the posterior π(θ|x) by incorporating observations x

summarized via the likelihood:

π(θ|x) =

f (x|θ)π(θ)

m(x)

. (8.1)

Here, m(x) normalizes the product f (x

|θ)π(θ) to be a density and is a constant

once the prior is speciﬁed and the data are observed. Given the data x and the

prior distribution, the posterior distribution

π(θ|x) summarizes all available

information about

θ.

Although the equation in (8.1) is referred to as a theorem, there is nothing

to prove there. Recall that the probability of intersection of two events A and B

was calculated as

P(AB) = P(A|B)P(B) = P(B|A)P(B) [multiplication rule in

(3.6)]. By analogy, the joint distribution of X and

θ, h(x,θ), would have two

representations depending on the order of conditioning:,

h(x,

θ) = f (x|θ)π(θ) =π(θ|x)m(x),

and Bayes’ theorem just solves this equation with respect to the posterior

π(θ|x).

To summarize, Bayes’ rule updates the probabilities of events when new

evidence becomes available, while Bayes’ theorem provides the recipe for up-

dating prior distributions of model’s parameters once experimental observa-

tions become available.

P(hypothesis)

BAYES’ RULE

−→ P(hypothesis|evidence)

π(θ)

BAYES’ THEOREM

−→ π(θ|data)

The Bayesian paradigm has many advantages, but the two most important

are that (i) the uncertainty is expressed via the probability distribution and

the statistical inference can be automated; thus it follows a conceptually sim-

ple recipe embodied in Bayes’ theorem; and (ii) available prior information is

coherently incorporated into the statistical model describing the data.

282 8 Bayesian Approach to Inference

The FDA guidelines document (FDA, 2010) recommends the use of a

Bayesian methodology in the design and analysis of clinical trials for medi-

cal devices. This document eloquently outlines the reasons why a Bayesian

methodology is recommended.

• Valuable prior information is often available for medical devices because of their

mechanism of action and evolutionary development.

• The Bayesian approach, when correctly employed, may be less burdensome than a

frequentist approach.

• In some instances, the use of prior information may alleviate the need for a larger

sized trial. In some scenarios, when an adaptive Bayesian model is applicable, the

size of a trial can be reduced by stopping the trial early when conditions warrant.

• The Bayesian approach can sometimes be used to obtain an exact analysis when

the corresponding frequentist analysis is only approximate or is too difﬁcult to imple-

ment.

• Bayesian approaches to multiplicity problems are different from frequentist ones

and may be advantageous. Inferences on multiple endpoints and testing of multiple

subgroups (e.g., race or sex) are examples of multiplicity.

• Bayesian methods allow for great ﬂexibility in dealing with missing data.

In the context of clinical trials, an unlimited look at the accumulated data

when sampling is of a sequential nature will not affect the inference. In the

frequentist approach, interim data analyses affect type I errors. The ability to

stop a clinical trial early is important from the moral and economic viewpoints.

Trials should be stopped early due to both futility, to save resources or stop

an ineffective treatment, and superiority, to provide patients with the best

possible treatments as fast as possible.

Bayesian models facilitate meta-analysis. Meta-analysis is a methodology

for the fusion of results of related experiments performed by different re-

searchers, labs, etc. An example of a rudimentary meta-analysis is discussed

in Sect. 8.10.

8.2 Ingredients for Bayesian Inference

A density function for a typical observation X that depends on an unknown

(possibly multivariate) parameter

θ is called a model and denoted by f (x|θ).

As a function of

θ, f (x|θ) = L(θ) is called the likelihood. If a sample x =

, x

,... , x

) is observed, the likelihood takes a familiar form, L(θ|x

,... , x

) =

f (x

|θ). This form was used in Chap. 7 to produce MLEs for θ.

Thus both terms model and likelihood are used to describe the distribution

of observations. In the standard Bayesian inference the functional form of f is

given in the same manner as in the classical parametric approach; the func-

tional form is fully speciﬁed up to a parameter

θ. According to the generally

accepted likelihood principle, all information from the experimental data is

summarized in the likelihood function, f (x

|θ) =L(θ|x

,... , x

8.2 Ingredients for Bayesian Inference 283

For example, if each datum X |θ were assumed to be exponential with the

rate parameter

θ and X

= 2, X

= 3, and X

= 1 were observed, then full in-

formation about the experiment would be given by the likelihood

θe

−2θ

×θe

−3θ

×θe

−θ

=θ

−6θ

This model is

exp

−

if the data are kept unspeciﬁed, but in the

likelihood function the expression

is treated as a constant term, as

was done in the maximum likelihood estimation (p. 233).

The parameter

θ, with values in the parameter space Θ, is not directly

observable and is considered a random variable. This is the key difference

between Bayesian and classical approaches. Classical statistics consider the

parameter to be a ﬁxed number or vector of numbers, while Bayesians express

the uncertainty about

θ by considering it as a random variable. This random

variable has a distribution

π(θ) called the prior distribution. The prior distri-

bution not only quantiﬁes available knowledge, but it also describes the un-

certainty about a parameter before data are observed. If the prior distribution

for

θ is speciﬁed up to a parameter τ, π(θ|τ), then τ is called a hyperparameter.

Hyperparameters are parameters of a prior distribution, and they are either

speciﬁed or may have their own priors. This may lead to a hierarchical struc-

ture of the model where the priors are arranged in a hierarchy.

The previous discussion can be summarized as follows:

The goal in Bayesian inference is to start with prior information on the

parameter of interest,

θ, and update it using the observed data. This is

achieved via Bayes’ theorem, which gives a simple recipe for incorporat-

ing observations x in the distribution of

θ, π(θ|x), called the posterior

distribution. All information about

θ coming from the prior distribution

and the observations are contained in the posterior distribution. The pos-

terior distribution is the ultimate summary of the parameter and serves

as the basis for all Bayesian inferences.

According to Bayes’ theorem, to ﬁnd

π(θ|x), we divide the joint distribution

of X and

θ (h(x, θ) = f (x|θ)π(θ)) by the marginal distribution for X, m(x),

which is obtained by integrating out

θ from the joint distribution h(x,θ):

m(x)

h(x, θ)dθ =

f (x|θ)π(θ)dθ.

The marginal distribution is also called the prior predictive distribution. Thus,

in terms of the likelihood and the prior distribution only, the Bayes theorem

can be restated as

π(θ|x) =

f (x|θ)π(θ)

f (x|θ)π(θ)dθ

284 8 Bayesian Approach to Inference

The integral in the denominator is a main hurdle in Bayesian computation

since for complex likelihoods and priors it could be intractable.

The following table summarizes the notation:

Likelihood, model f (x|θ)

Prior distribution

π(θ)

Joint distribution h(x,

θ) = f (x|θ)π(θ)

Marginal distribution m(x) =

f (x|θ)π(θ)dθ

Posterior distribution π(θ|x) = f (x|θ)π(θ)/m(x)

We illustrate the above concepts by discussing a few examples in which

one can ﬁnd the posterior distribution explicitly. Note that the marginal dis-

tribution has the form of an integral, and in many cases these integrals cannot

be found in a ﬁnite form. It is fair to say that the number of likelihood/prior

combinations that lead to an explicit posterior is rather limited. However, in

the general case, one can evaluate the posterior numerically or, as we will see

later, simulate a sample from the posterior distribution. All of the above, ad-

mittedly abstract, concepts will be exempliﬁed by several worked-out models.

We start with the most important model in which both the likelihood and prior

are normal.

Example 8.1. Normal Likelihood with Normal Prior. The normal likeli-

hood and normal prior combination is important because it is frequently used

in practice. Assume that an observation X is normally distributed with mean

θ and known variance σ

. The parameter of interest, θ, is normally distributed

as well, with its parameters

µ and τ

. Parameters µ and τ

are hyperparam-

eters, and we will consider them given. Starting with our Bayesian model of

|θ ∼ N (θ,σ

) and θ ∼ N (µ,τ

), we will ﬁnd the marginal and posterior dis-

tributions. Before we start with a derivation of the posterior and marginal, we

need a simple algebraic identity:

A(x

−a)

+B(x −b)

=(A +B)(x − c)

A +B

−b)

,for c =

Aa +Bb

A +B

. (8.2)

We start with the joint distribution of (X ,

θ), which is the product of two

distributions:

h(x,

θ) =

2πσ

exp

−

2σ

(x −θ)

2πτ

exp

−

2τ

(θ −µ)



The exponent in the joint distribution h(x,θ) is

8.2 Ingredients for Bayesian Inference 285

−

2σ

(x −θ)

−

2τ

(θ −µ)

which, after applying the identity in (8.2), can be expressed as

−

+τ

2σ

θ −

+τ

x +

+τ

¶¶

−

2(σ

+τ

)

−µ)

. (8.3)

Note that the exponent (8.3) splits into two parts, one containing

θ and the

other

θ-free. Accordingly the joint distribution h(x,θ) splits into the product of

two densities. Since h(x,

θ) can be represented in two ways, as f (x|θ)π(θ) and

π(θ|x)m(x), by analogy to P(AB) = P(A|B)P(B) = P(B|A)P(A), and since

we started with f (x

|θ)π(θ), the exponent in (8.3) corresponds to π(θ|x)m(x).

Thus, the marginal distribution simply resolves to X

∼ N (µ, σ

+τ

) and the

posterior distribution of

θ comes out to be

θ|X ∼N

+τ

X +

+τ

µ,

+τ

Bellow is a speciﬁc example of our ﬁrst Bayesian inference.

Example 8.2. Jeremy’s IQ. Jeremy, an enthusiastic bioengineering student,

posed a statistical model for his scores on a standard IQ test. He thinks that,

in general, his scores are normally distributed with unknown mean

θ (true

IQ) and a variance of

= 80. Prior (and expert) opinion is that the IQ of

bioengineering students in Jeremy’s school,

θ, is a normal random variable,

with mean

µ = 110 and variance τ

= 120. Jeremy took the test and scored

= 98. The traditional estimator of θ would be

θ = X = 98. The posterior

is normal with a mean of

120

80+120

×98+

80+120

×110 = 102.8 and a variance of

80×120

80+120

=48. We will see later that the mean of the posterior is Bayes’ estimator

θ, and a Bayesian would estimate Jeremy’s IQ as 102.8.

If n normal variates, X

, X

,... , X

, are observed instead of a single obser-

vation X , then the sample is summarized as

X and the Bayesian model for θ

is essentially the same as that for the single X , but with σ

/n in place of σ

In this case, the likelihood and the prior are

X |θ ∼N

θ,

and θ ∼N (µ,τ

producing

θ|X ∼N

+τ

X +

+τ

µ,

+τ

286 8 Bayesian Approach to Inference

Notice that the posterior mean

+τ

X +

+τ

is a weighted average of the MLE X and the prior mean µ with weights w =

nτ

/(σ

+nτ

) and 1−w =σ

/(σ

+nτ

). When the sample size n increases, the

contribution of the prior mean to the estimator diminishes as w

→ 1. On the

other hand, when n is small and our prior opinion about

µ is strong (i.e., τ

small), the posterior mean remains close to the prior mean

µ. Later, we will

explore several more cases in which the posterior mean is a weighted average

of the MLE for the parameter and the prior mean.

Example 8.3. Suppose n

=10 observations are coming from N (θ,10

). Assume

that the prior on

θ is N (20,20). For the observations

{2.944,−13.361,7.143,16.235,−6.917,8.580, 12.540, −15.937, −14.409,5.711}

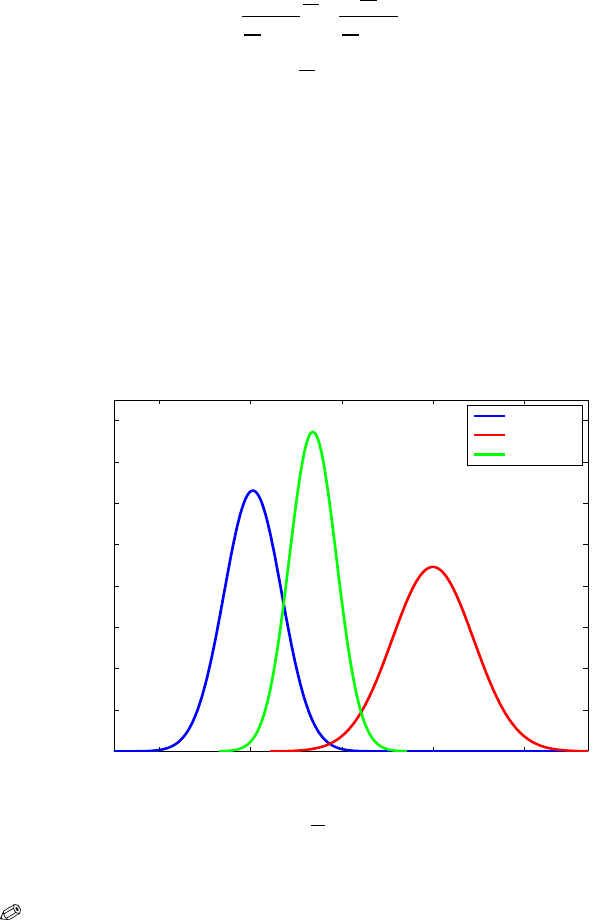
the posterior is N (6.835,6.667). The three densities are shown in Fig. 8.2.

−10 0 10 20 30

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

likelihood

prior

posterior

Fig. 8.2 The likelihood centered at MLE X = 0.2529, N (0.2529, 10

/10) (blue), N (20, 20)

prior (red), and posterior for data

{2.9441,−13.3618, ...,5.7115} (green).

8.3 Conjugate Priors 287

8.3 Conjugate Priors

A major technical difﬁculty in Bayesian analysis is ﬁnding an explicit posterior

distribution, given the likelihood and prior. The posterior is proportional to the

product of the likelihood and prior, but the normalizing constant, marginal

m(x), is often difﬁcult to ﬁnd since it involves integration.

In Examples 8.1 and 8.3, where the prior is normal, the posterior distribu-

tion remains normal. In such cases, the effect of likelihood is only to “update”

the prior parameters and not to change the prior’s functional form. We say that

such priors are conjugate with the likelihood. Conjugacy is popular because of

its mathematical convenience; once the conjugate pair likelihood/prior is iden-

tiﬁed, the posterior is found without integration. The normalizing marginal

m(x) is selected such that f (x

|θ)π(θ) is a density from the same class to which

the prior belongs. Operationally, one multiplies “kernels” of likelihood and pri-

ors, ignoring all multiplicative terms that do not involve the parameter. For

example, a kernel of gamma

G a(r,λ) density f (θ|r,λ) =

r−1

Γ(r)

−λθ

would be

r−1

−λθ

. We would write: f (θ|r,λ) ∝ θ

r−1

−λθ

, where the symbol ∝ stands

for “proportional to.” Several examples in this chapter involve conjugate pairs

(Examples 8.4 and 8.6).

In the pre-Markov chain Monte Carlo era, conjugate priors were exten-

sively used (and overused and misused) precisely because of this computa-

tional convenience. Today, the general agreement is that simple conjugate

analysis is of limited practical value since, given the likelihood, the conjugate

prior has limited modeling capability.

There are quite a few instances of conjugacy. The following table lists sev-

eral important cases. For practice you may want to derive the posteriors in

Table 8.1. It is recommended that you consult Chap. 5 on functional forms of

densities involved in the Bayesian model.

Example 8.4. Binomial Likelihood with Beta Prior. An easy, yet impor-

tant, example of a conjugate structure is the binomial likelihood and beta

prior. Suppose that we observed X from a binomial

B in(n, p) distribution,

f (x

|θ) =

(1 − p)

n−x

and that the population proportion p is the parameter of interest. If the prior

on p is beta

B e(α, β) with hyperparameters α and β and density

π(p) =

B(α, β)

α−1

(1 − p)

β−1

the posterior is proportional to the product of the likelihood and the prior

π(p|x) =C · p

(1 − p)

n−x

· p

α−1

(1 − p)

β−1

=C · p

x+α−1

(1 − p)

n−x+β−1