Вернер М. Основы кодирования

Подождите немного. Документ загружается.

8.1.

Дифференциальная энтропия

113,

Из

теории информации

следует,

что

дифференциальная энтропия

достигает своего максимума

при

гауссовском распределении вероят-

ности.

Теорема

8.1.1. При заданной дисперсии

максимальной диффе-

ренциальной энтропией обладает источник

гауссовским

распреде-

лением,

вероятности, причем,

HGaus(X)

= ~

' бит. (8.6)

Пример:

Дифференциальная энтропия гауссовского источника.

Из

(8.5)

следует,

что

дифференциальная энтропия гауссовского

источника равна

ЩХ)

+ОО

Выражение

квадратных скобках может быть разложено

на два

ин-

теграла. Таким образом, окончательно имеем

°° • ,2

ехр (

2<T

V2^J

V 2a

dx =

нат

Численные примеры

для

трех,

наиболее употребительных распреде-

лений,

приведены

таблице

8.1.

Пример:

Телефония.

Практическая

польза приведенных выше результатов может быть

наглядно показана

при

помощи оценки достижений скорости пере-

дачи информации

(в

битах)

цифровых телефонных линиях. Совре-

менные стандартные методы цифровой передачи речи (логарифми-

ческие РСМ)

требуют

затраты

8 бит на

кодирование одного отсчета,

114

Глава

Непрерывные

источники

каналы

Таблица

8.1. Пример дифференциальной энтропии.

Распределе-

ния

Равномерное

Лапласа

Гауссовское

Функция

плотности распределения

вероятности

д*)

| s;

fix) -

fix) *

д для |i| <

\/Z

0 consi

expf V2

)

(

eXP

2a2j

Дифференциальная

энтропия

Jn(2v/5cr)

1п(\/2(те)

1п(2тг(Т

е)

21n2

1,79

1,94

-2,04

при

частоте отсчетов 8 кГц. Таким образом, скорость передачи речи

составляет 64 кбит/сек.

Исходя из равномерного распределения вероятностей в интервале

[-1,1],

опытным

путем

получим а

= 1/3. Таким образом, дифферен-

циальная

энтропия на один отсчет составляет

H{X)

бит

(8.9)

Так

как отсчеты производятся с частотой 8 кГц, получаем, что

необходимая скорость передачи речи составляет 8 кбит/сек. При

оценке

энтропии мы не принимали во внимание связи

между

сосед-

ними

отсчетами (память источника) и, поэтому, реальная дифферен-

циальная

энтропия источника речи

будет

еще меньше. В самом деле,

мы знаем, что современные алгоритмы кодирования речи позволя-

ют осуществлять передачу речевого сигнала со скоростью около 8

кбит/сек при качестве, сравнимом со стандартным РСМ.

8.2.

Пропускная способность канала и граница

Шеннона

Аналогично дискретным каналам, можно определить пропускную

способность для непрерывных каналов. Будем искать, как и ранее,

8.2.

Пропускная

способность

канала

граница

Шеннона

наибольшее значение переносимой информации

по

всем возможным

функциям

плотностей распределения вероятностей.

C =

supI(X;Y).

(8.10)

/(*)

Поиск

точной верхней грани,

общем

случае,

представляет собой

довольно сложную

задачу.

Рассмотрим важнейший частный случай-

передачу информации

по

каналу

аддативным белым гауссовским

шумом (АБГШ)

ограниченной полосой. Модель такого канала изоб-

ражена

на рис. 8.4. Для

гауссовского распределения вероятности

амплитуды сигнала

на

входе

канала получаем формулу пропускной

способности канала, хорошо известную

теории информации.

Ограниченный

по

полосе

канал

Источник* '#"••

*,•* •.

**»*>

•*.>..%..".

**„

•

ИСТОЧНИКУ

Спектральная

плотность

мощности

шума

$NN lo>)

N„/2.

Рис.

8.4.

Модель

ограниченного

по

полосе

канала

АБГШ.

Теорема 8.2.1.

Пропускная

способность

канала (Хартлей

- Шен-

нон).

Пропускная

способность идеального канала

шириной полосы

пропускания

В и

аддитивным белым гауссовским шумом мощности

равна

-|).

(8.11)

бит/сек

Здесь,

как и

ранее,

5 -

мощность сигнала

полосе пропускания

канала. Размерность

С -

бит/сек.

Для интерпретации пропускной способности непрерывного кана-

ла-С,

рассмотрим выражение

(8.11)

при

ширине полосы пропуска-

ния,

равной

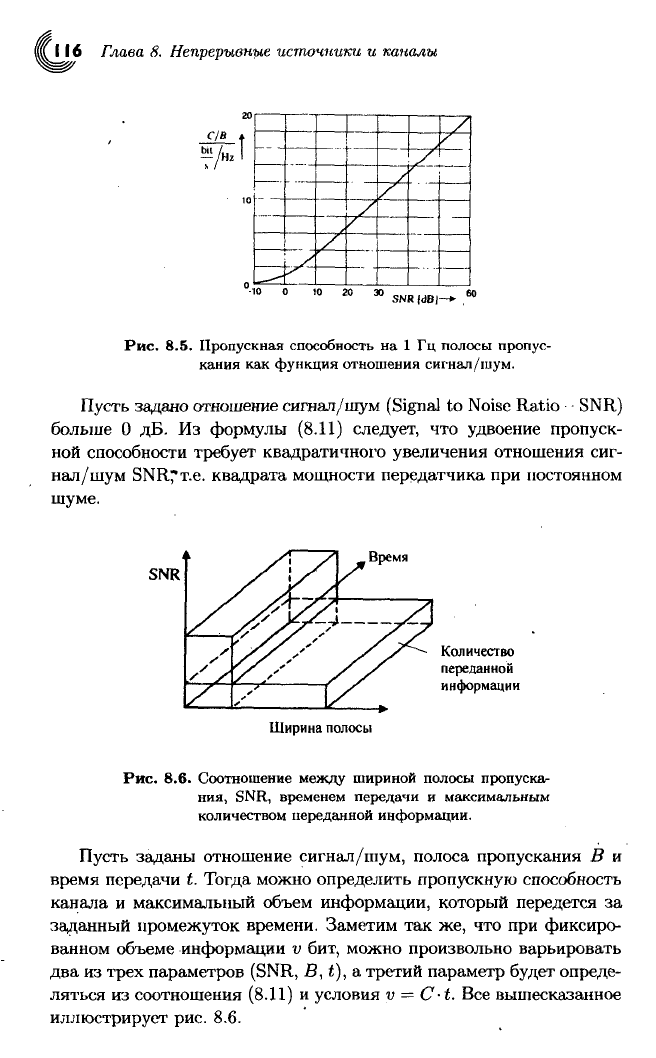
1 Гц (рис. 8.5).

Можно отметить асимптотически

ли-

нейный

характер поведения функции

С/В =

log

f(S/N)

(рис. 8:5

выполнен

полулогарифмическом масштабе).

16 Глава 8. Непрерывные источники и каналы

С/В

— /Hz

-—

У \—

—

Рис.

8.5.

Пропускная способность

на 1 Гц

полосы пропус-

кания как функция отношения

сигнал/шум.

Пусть задано отношение сигнал/шум (Signal

Noise Ratio

SNR)

больше

0 дБ. Из

формулы (8.11) следует,

что

удвоение пропуск-

ной

способности требует квадратичного увеличения отношения сиг-

нал/шум SNR?T.e. квадрата мощности передатчика при постоянном

шуме.

SNR

Время

Количество

переданной

информации

Ширина

полосы

Рис.

8.6.

Соотношение

между

шириной полосы пропуска-

ния,

SNR,

временем

передачи

максимальным

количеством

переданной информации.

Пусть заданы отношение сигнал/шум, полоса пропускания

В и

время передачи

Тогда можно определить пропускную способность

канала

максимальный объем информации, который передется

за

заданный

промежуток времени. Заметим так же, что при фиксиро-

ванном

объеме информации

бит, можно произвольно варьировать

два из трех параметров (SNR,

В, t), а

третий параметр

будет

опреде-

ляться из соотношения (8.11)

условия г;

= С-t.

Все вышесказанное

иллюстрирует рис.

8.6.

8.2. Пропускная

способность

капала и

граница-Шеннона

Из

рис. 8.6 видно, что объем передаваемой информации за опре-

деленное время можно представить как объем параллелепипеда в

координатах SNR, But.

При

внимательном рассмотрении соотношения (8.11), возникает

важный вопрос; Как

будет

меняться пропускная способность канала

при

стремлении ширины полосы пропускания к бесконечности? От-

вет не очевиден, так как расширение полосы влечет за собой увеличе-

ние

мощности шума N. Мощность шума при постоянной спектраль-

ной

плотности No пропорциональна ширине полосы пропускания.

Чем шире полоса, тем больше шум на выходе приемника (рис. 8.7).

= N

B. (8.12)

(co)

"* со

-ЪсВ 0 2яВ

Рис.

8.7. Спектр белого гауссовского шума в ограниченной

полосе

Исследуем предельный переход

°° = lim

—Ц—=

lira Bln(l.+-§)log

e. (8.13)

бит/сек в-оо бит/сек в-^оо N' *

Замечание. Мы

использовали

натуральный

логарифм

для

упроще-

ния

вычисления

предела.

Переход

от

размерности

пропуской

способ-

ности

нат/сек

размерности

бит/сек

достигается

умножением

правой

части

вырамсения

(8.13) на Iog

(e).

Подставляя (8.12) в предельный переход (8.13), получаем неопре-

деленность

В—юо

Раскрывая неопределенность по правилу Лапиталя, получаем конеч-

ное значение предела

^"h

15)

Выражение (8.15) совместно с (8.13) определяет

границу

Шеннона.

Глава

Непрерывные

источники

каналы

Пропускная

способность непрерывного канала с АБГШ и неогра-

ниченной

полосой пропускания равна

^^-«#log

e«l,44-J.

(8.16)

бит/сек

No No

В технике связи при передаче цифровой информации часто ис-

пользуется относительная величина

энергия

сигнала

Еъ, приходя-

щаяся

на бит переданной информации. Так как максимальная ско-

рость передачи информационных бит/сек определяется как

минимальная

длительность передачи одного бита равна

(8.18)

Энергия,

затрачиваемая на передачу бита.информации, определяет-

ся

произведением Еъ =

-Тъ-

Используя (8.18)

(8.16), переходим

следующему утверждению.

Для передачи одного бита цифровой информации необходимо,

чтобы отношение энергии

на

бит

Еъ к

спектральной

плотности

мощности

белого гауссовского шума No равнялось, как минимум

«0,69^-1,59

dB. (8.19)

min

Замечание.

Заметим, что

литературе

спектральная

плотность

шума

иногда

определяется

не как No/2,

как No. Это

приводит

появлению

дополнительного

слагаемого

правой

части

(8.19), рав-

ного

1,42 дВ.

Наглядно

связь между SNR,

В и

битовой скоростью

можно

представить

виде дааграммы. Для этого, прежде всего, формально

подставим

вместо

и NQB вместо

N в

(8.11), разрешим равенство

относительно

S/{NQB)

получим

R/B

1. (8.20)

Устраним зависимость левой части от полосы пропускания

пу-

тем умножения обеих частей (8^20) на B/R, получим

8.2. Пропускная

способность

канала и

граница

Шеннона

I 19)

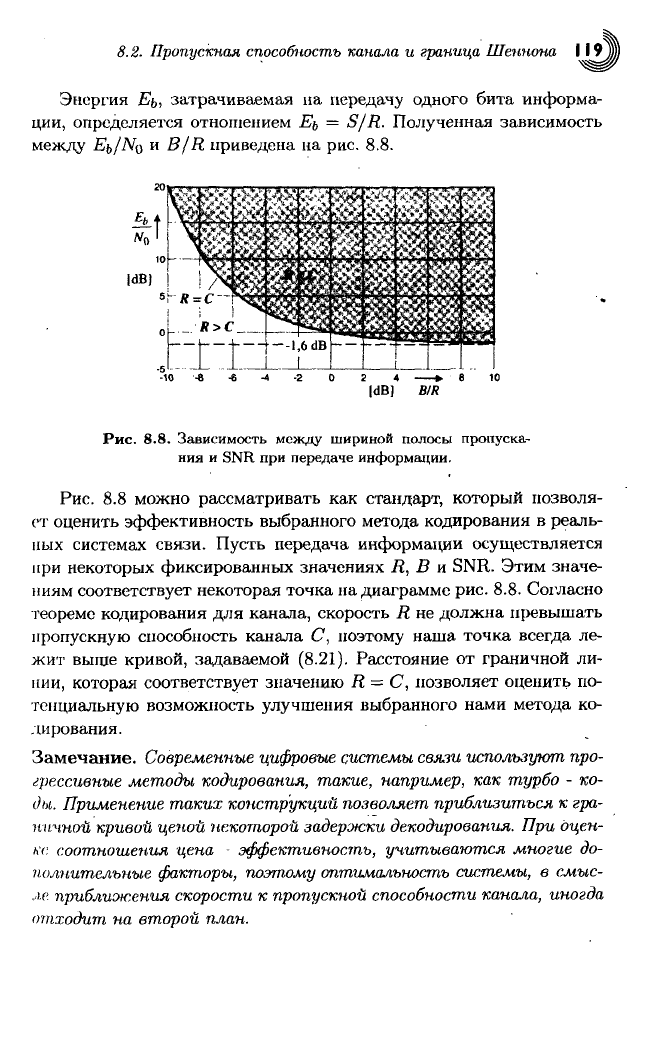
Энергия Еь, затрачиваемая на передачу одного бита информа-

ции,

определяется отношением Еь = S/R. Полученная зависимость

между

ЕЬ/NQ

И B/R приведена на рис. 8.8.

IdB]

Рис.

8.8. Зависимость между шириной полосы пропуска-

ния

и SNR при передаче информации.

Рис.

8.8 можно рассматривать как стандарт, который позволя-

ет оценить эффективность выбранного метода кодирования в реаль-

ных системах связи. Пусть передача информации осуществляется

при

некоторых фиксированных значениях R, В и SNR. Этим значе-

ниям

соответствует некоторая точка на диаграмме рис. 8.8. Согласно

теореме кодирования для канала, скорость R не должна превышать

пропускную способность канала С, поэтому наша точка всегда ле-

жит выще кривой, задаваемой (8.21). Расстояние от граничной ли-

нии,

которая соответствует значению R = С, позволяет оценить по-

тенциальную возможность улучшения выбранного нами метода ко-

дирования.

Замечание.

Современные

цифровые

системы

связи

используют

про-

грессивные

методы

кодирования,

такие,

например,

как

турбо

- ко-

ды.

Применение

таких конструкций

позволяет

приблизиться

к гра-

ничной

кривой

ценой

некоторой

задержки

декодирования.

При

оцен-

ки

соотношения

цена

эффективность,

учитываются

многие

до-

полнительные

факторы,

поэтому

оптимальность

системы,

смыс-

ле

приближения

скорости

пропускной

способности

канала,

иногда

отходит

на

второй

план.

Глава 8. Непрерывные источники и каналы

8.3.

Примеры

Пример:

Видеотелефония.

Рассмотрим возможность передачи изображений

между

абонен-

тами телефонной сети стандарта

ISDN.

этой системе 'для пере-

дачи двумерных изображений используется канал

со

скоростью

кбит/сек, поэтому, необходимо, чтобы поток видеоинформации

был

сжат

до

этой величины. При этом, алгоритм сжатия должен

устра-

нять

как

избыточность

точки зрения теории информации,

так и

детали изображения, не существенные

для

абонента или многократ-

но

повторяющиеся. Одной

из

таких деталей может быть, например,

не

меняющийся длительное время второй план изображения

и т.д.

В дальнейшем, мы рассмотрим пример идеального сжатия видеосиг-

нала.

При

вычислении необходимой скорости передачи данных, мы

бу-

дем исходить

из

стандарта

QCIF

(

Quarter Common Intermediate For-

mat).

В этом стандарте

для

передачи цветных изображений использу-

ется один сигнал яркости

(У) и два

сигнала цветности ([/,

V). Па-

раметры этих сигналов приведены

таблице

8.2.

Таблица

8.2.

Пример сигналов для передачи изображений.

Сигнал ярко-

сти

(У)

Сигнал цвет-

ности

({/, V)

Количество

точек

строке

176

Количество

строк

кадре

144

(120)

72(

66)

Количество

бит

на точ-

ку

Частота

сме-

ны

кадров

5...

15 Гц

5...

15 Гц

Из

табл.

8.2

следует,

что

отображение цветного изображения

на

экране

достигается

помощью четырехточечных матриц,

каждую

из

которых глаз воспринимает как одну точку. Внутри матрицы

две

Видеосигнал

стандартах

QCIF

PAL и

SEC AM содержит

- 288

строк

и 352

точки

строке

для

сигнала яркости

(Y) и два

сигнала цветности

(V', V) по 176

строк

и 144

точки

на

каждый,

для

видеосигнала

стандарте

QCIF

NTSC

- 240

строк

по 352

точки

строке

(Y) и,

соответственно,

120

строк

и 144

точки

(U, V).

Прим.

перев.

8.3.

Примеры

точки принадлежат сигналу одной цветности, а две -

другому.

Яр-

кость каждой точки определяется сигналом У, который квантуется

на

= 256 уровней. Будем считать, что смена кадров производится

с частотой 10 Гц. При быстром движении камеры и относительно

медленной смене кадров, на экране возникают, так называемые, раз-

мывания

изображения.

1. Найдите информационый поток в видеоканале при условии,

что частота смены кадров равна 10 Гц. Будем исходить из сле-

дующей упрощенной модели: проквантованные видеосигналы

имеют равномерное распределение вероятности во времени и

пространстве и взаимно независимы.

2. Найдите минимальную ширину полосы пропускания идеально-

го телевизионного приемника, если

требуемое

для удовлетво-

рительного качества изображения отношение сигнал/шум со-

ставляет 30 дБ.

Решение.

Из

табл.

8.2

следует,

что

число символов, необходимых

для

передачи кадра, равно

Л/с

= 176

•

144 + 2

•

72 =

38016.

(8.22)

символ

Так

как частота смены кадров равна 10 Гц, скорость передачи

символов составляет

= N

- 10 Гц =

3800160

символ/сек.

(8.23)

Учитывая, что вероятности 2

= 256 возможных квантованных зна-

чений

амплитуд сигналов Y, U, V распределены равномерно,

инфор-

мация

каждого символа равна

/» = - log, --£ = 8 бит/символ.

(8.24)

символ

Таким

образом, искомый информационный поток составляет

/ =

380160

символ

. 8

биТ

3,04128

Мбит/сек.

(8.25)

сек

символ

Замечание.

Заметим,

что

информация

символа

равна

длине

дво-

ичной

записи

символа

только

случае

равномерного

распределения

Глава

Непрерывные

источники

каналы

вероятностей

символов.

реальных

каналах

передани

цифровых

ви-

деосигналов

информация

одного

символа

существенно

меньше

8 бит.

Сравнение

(8.25) с ISDN-В

каналом,

по

которому

информация

пере-

дается

со

скоростью

кбит/сек

показывает,

что

фактор

сжатия

этом

канале

должен

быть

равен,

приблизительно,

50.

2. Для передачи информационного потока

3,04128

Мбит/сек дол-

жен использоваться канал с большей пропускной способностью. Из

шенноновской

формулы

(8.11)

получаем

В > ^_

3,04128-10»

и 305

log(l

+ #) Io

(l +103)

ц v ;

Пример:

Импульсно-кодовая модуляция.

Аналоговый сигнал с верхней спектральной частотой 4 кГц под-

вергается дискретизации во времени с частотой отсчетов, в 1,25 раз

превышающей минимально

необходамую

для восстановления сигна-

ла. Каждый

отсчет

квантуется на 256 уровней символами, содер-

жащими 8 бит. Предполагается, что символы независимы и имеют

равномерное распределение вероятностей.

1. Найдите информационный поток оцифрованного источника.

2. Может ли этот информационный ноток быть нередан по каналу

с АБГШ с полосой В = 10 кГц и SNR—20 дБ с пренебрежимо

малой вероятностью ошибки?

3. Каково должно быть минимальное SNR, необходимое для пе-

редачи информационного потока в полосе В = 10 кГц с прене-

брежимо малой вероятностью ошибки?

4. Каково минимальное значение полосы пропускания В, обес-

печивающее передачу информации по каналу с АБГШ при

SNR-20 дБ с пренебрежимо малой вероятностью ошибки?

Решение.

1. Частота отсчетов равна

1,25-4-2

= 10 кГц.

(8.27)

Скорость передачи символов равна

= 10

сим/сек. (8.28).