Вернер М. Основы кодирования

Подождите немного. Документ загружается.

2.1.

Информация одного события

В качестве простейшего примера можно привести двоичный

ис-

точник

без

памяти

алфавитом

X = {х\ =

0, £2

= 1} и

вероят-

ностями

0 < р\ < 1 и Р2 = 1 ~

Р\

•

Выбор очередной цифры

про-

изводится независимо

от

прежних

последующих выборок. Изоб-

ражение простейшего источника приведено

на

рис.

2.1.

Рассмотрим

вначале одиночные события. Повседневный опыт подсказывает,

что

часто происходящие события,

так же

как

их

вероятности,

дают

нам

мало информации. Возьмем, например, сообщение «собака укусила

человека».

Это

привычное известие

не

привлекло

бы к

себе никако-

го внимания,

в то

время,

как

сообщение «человек

укусил

собаку»

вес газеты напечатали

бы

крупным шрифтом.

Из

этого можно

сде-

лать вывод: частые, ожидаемые события

несут

мало информации

и,

наоборот, редкие,

т.е.

неожиданные события,

обладают

высоким

ин-

формационным

содержанием. Следовательно, информация

вероят-

ность находятся

обратно пропорциональной зависимости. Исходя

из

этого, введем понятие количества информации,

как

измеряемой

величины

на

основании

следующих

трех

аксиом

[1].

Рис.

2.1.

Простейший источник источник информации

ал-

фавита

AT.

Аксиомы

для

определения количества информации

[1]

1. Информация одиночного события

Х{

£ X,

происходящего

с ве-

роятностью

pi,

имеет положительное значение

•

(2.1)

2. Совместная информация

двух

независимых событий

(xi,Xj)

совместной вероятностью

P(xi,Xj)

= Pij =

•

Pj>

равна

сумме

их информации

(2.2)

3. Информация является непрерывной функцией

от

вероятности

события.

Аксиомы

1 и 2

утверждают,

что

информация нескольких событий

не

может взаимно уничтожаться. Аксиома

вводит понятие совмест-

ной

информации событий.

Из

аксиомы

следует,

что

небольшое

из-

менение вероятности события приводит

небольшому изменению

ее

Глава 2. Информация, энтропия и избыточность

информации.

Аксиома

определяет информацию

двух

независимых/

событий.

Из (2.2)

следует,

что

информация события определяется/

как

логарифмическая функция

ее

вероятности. Следовательно,

ин-

формацию

можно определить следующим образом:

Информация

события,

происходящего

вероятностью

р,

равна

1(р)

-Iog

(p)

с [/] = бит.

(2.3)

В данной формуле используется двоичный логарифм. Возможны

сле-

дующие обозначения двоичного логарифма: Iog

(a;)

= Id (x) =

lb(a;),

где

под Id

подразумевается термин дуальный логарифм,

а под

1Ь

бинарный.

Иногда используют натуральный логарифм

единицей

измерения

наш,

но

можно использовать

любую

единицу измерения

информации.

Можно также переходить

от

одной единице

другой,

применяя

формулу пересчета:

k>g

(z)

log

(ar)/log

(a)

log

(z)

•

log

(6).

Размерность

бит

используется

информационной технике

при

двоичной системы исчисления. Как

будет

показано

следующих раз-

делах,

двоичная система очень удобна при описании процесса приня-

тия

решения, когда

на

любой вопрос

существует

только

два

ответа:

«да»

или

«нет».

[10] приведена наглядная интерпретация понятия

«бит».

Up)

бит

V—-

Невозможное

событие

= 0

Неизбежное

событие

0,5 р • 1

Рис.

2.2.

Информация символа

7(р) с

вероятностью появ-

ления

р.

На

рис.

2.2

показано поведение информации как функции вероят-

ности.

Информация постоянно происходящего события равна нулю.

В отечественной математической литературе

для

обозначения двоичного

и на-

турального логарифма принято использовать

log

In.

Прим.

перев.

2.2.

Энтропия

избыточность

15,

ростом неопределенности информация также растет

и для

невоз-

\можного

события

стремится

бесконечности. Таким образом,

ин-

формация

соответствует всем приведенным ранее рассуждениям

удовлетворяет аксиомам

1 - 3. С

точки зрения теории вероятности,

определение информации можно рассматривать как некоторое отоб-

ражение событий. Аналогичное отображение имеют стохастические

переменные.

следующих разделах это

будет

поясняться

на

приме-

рах.

2.2. Энтропия

избыточность

После того,

как

информация отдельного события определена,

рас-

смотрим источник событий.

Для его

описания

будем

использовать

информацию,

которую несут содержащиеся

нем события. По ана-

логии

термодинамикой введем понятие энтропии.

термодинамике

энтропия

является мерой неупорядоченности системы.

теории ин-

формации

энтропия определена как мера неопределенности источни-

ка.

Используя информацию отдельных событий, выразим энтропию

источника следующим образом:

Элтропия

простейшего источника

без

памяти

X с

алфавитом

X —

{х\,х<2,

• • •

,£JV}

соответствующим вероятностям

Р\,Р2,

• • •

,PN

равна

H(x)

= ^2-

\og

(

)6nT. (2.4)

Представим себе игру,

которой некоторое событие источника долж-

но

быть предсказано. Если источник

отдает

предпочтение опреде-

ленному событию, смело ставьте

на

него

и, в

основном,

вы

будете

выигрывать. Если

все

события равновероятны,

то

ставьте

на

любое

событие: если неопределенность источника максимальна, шансы

на

выигрыш минимальны.

Пример:

Оценка энтропии.

Поясним

эту

связь

на

примере простейшего дискретного источ-

ника

без

памяти

из

табл.

2.1.

Информация источника представля-

ет собой

результат

эксперимента

со

случайными событиями

а,

Ь,

с,

Пусть

результате

повторения этого эксперимента

мы

получаем по-

следовательность

{а,Ъ,а,d

а,а,с,d,b,a,a,b,...}.

(2.5)

Глава 2. Информация, энтропия и избыточность

Таблица 2.1.

Дискретный источник

без

памяти

символами

алфавита

X = {а,

Ь,

с,

d} с

вероятностью

р* и

информацией

I(pi).

Символ

р.

ПР.)

1/2

бит

1/4.

бит

1/8

бит

1/8

бит

Подставив

на

место каждого события

его

информацию, получим

типичную функцию стохастического процесса

{/[п]/бит}

{1,2,1,3,1,1,3,3,2,1,1,2,...}.

(2.6)

Предположим

эргодичность

(постоянство поведения) такого про-

цесса

во

времени. Такую эргодичность

мы,

например, предполагаем

при

бросании монетки

или

игрального кубика.

ростом числа

ис-

пытаний

среднее значение информации источника

JV-1

lim -i у

/[га]

N->oo

N t-*

n=0

стремится

математическому

ожиданию

(2.7)

(2.8)

Таким

образом, учитывая сходимость ряда

(2.7)

математическому

ожиданию, получаем практическую меру

для

информации источни-

ка.

рассмотренном нримере математическое ожидание

Е{1)

равно

1,75 бит.

Из

первых

испытаний

мы

также получаем оценку

для

/(га)

1,75

бит.

Проводя аналогичные рассуждения, Шеннон

[1]

заложил

опре-

деление энтропии

три

следующие аксиомы.

Аксиоматическое определение энтропии

1. Энтропия

Н{Х) =

f(pi,P2,

• • •

,PN) является непрерывной функ-

цией

вероятностей р\,Р2,...

,ры-

Для

источников

одинаковой вероятностью событий

pi = jj

энтропия

увеличивается

ростом числа событий

3. Разложение процедуры выбора событий

на

несколько этапов

не

изменяет энтропию (процедуру выбора можно свести

последо-

вательным двоичным решениям).

2.2.

Энтропия

избыточность

Пример:

Разложение процедуры выбора.

\ Данный пример поясняет аксиому

Рассмотрим

три

события

a, b

с.

которые происходят

соответственными вероятностями

1/2,1/3

1/6. Для

того, чтобы выбрать одно

из

этих

трех,

мы

можем поста-

вить

два

независимых вопроса (рис.

2.3).

1/6

"о,

Рис.

2.3.

Разложение процесса выбора символов.

На

эти вопросы

могут

быть даны только

два

ответа:

или «да» или

«нет».

Согласно аксиоме

(3), к

энтропии предъявляется

следующее

требование:

причем,

второй вопрос задается

вероятностью

1/2. Мы

покажем

общем виде (рис.

2.4), что

определение энтропии

(2.8)

удовлетворяет

требованию аксиомы (НЗ).

Рг(Ь)

О Ь

Ь=с

Рис.

2.4.

Разложение процедуры принятия решения.

Для

разложенной

энтропии получаем

Н(Х)

бит

-Pi(a)log

(pi(a)) -Pi(a)log

(pi(a))+

(о)[-рг(Ь) Iog

(b))

- Mb)

Iog

(b))],

где вероятности определяются следующим образом

Pi(a)

=р(Ь)+р(с),

(2.10)

(2.11)

Глава

Информация,

энтропия

избыточность

Р2(6)

Р(Ь)

Р2

(Ь)

р(сУ

Замечание.

Последнее

равенство

подтверждается

постановкой

экс-

перимента

со

случайными

событиями.

Пусть

событие

произошло

300 раз,

событие

Ь - 200, а

событие

с - 100 раз.

Частота

каждого

события

данном

примере,

равна

его

вероятности.

Если мы

отбро-

сим

событие

а, то

останется

300

выборок

событий

Ь и с,

частоты

выборок

этих

событий

удвоятся,

но их

отношение

не

изменится.

Из

(2.11)- (2.13) следует, что вероятности на втором шаге можно

выразить как

Подставляя полученные выражения в формулу для энтропии, имеем

-д— = -Pi(a)log

(pi(o)) -Pi(a)log

(pi(a))+

Pl(t

что после упрощений соответствует энтропии без разложения про-

цесса выбора событий

(o) lo

(

(a)) - р(Ь) lo

(p(6)) - р(с) Iog

(p(c)). (2.17)

В рассмотренном примере было использовано свойство

логариф-

мической

функции, переводящее произведение в сумму. Определение

(2.4) является единственным, при котором аксиома 3 имеет силу.

Заметим также, что рассмотренное разложение процесса выбора со-

бытий может быть сведено к последовательности бинарных решений

«да»

«нет».

Максимальной неопределенности соответствует макси-

мальная энтропия источника. Сформулируем следующую теорему:

2.2.

Энтропия

избыточность

19)

Теорема

2.2.1. Энтропия простейшего дискретного источника без

памяти

максимальна, если все события, в нем содержащиеся, име-

ют одинаковую вероятность, В этом

случае

энтропия просто равна

логарифму числа событий

#о

Ьит.

(2.18)

Замечание.

Последующее

доказательство

теоремы

является

ти-

пичным

теории

информации.

В таких

доказательствах

использу-

ются

оценки

предельные

переходы,

которые

ранее

были

известны,

но не

находили

практического

применения.

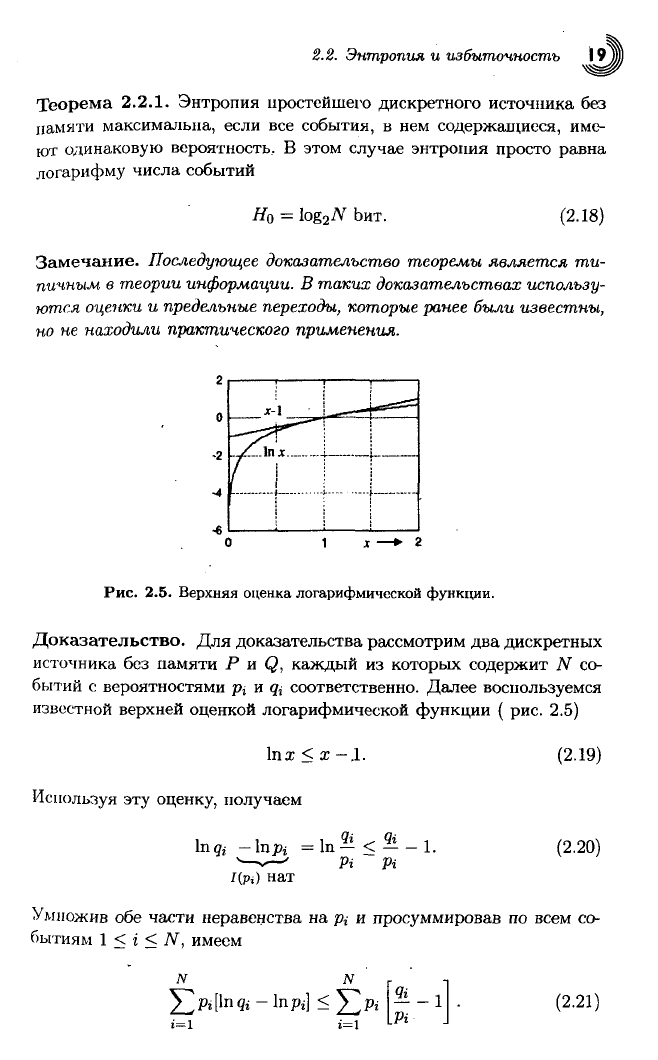
Рис.

2.5. Верхняя оценка логарифмической

функции.

Доказательство.

Для доказательства рассмотрим два дискретных

источника

без памяти Р и Q, каждый из которых содержит N со-

бытий с вероятностями р{ и

соответственно. Далее воспользуемся

известной

верхней оценкой логарифмической функции ( рис. 2.5)

lnx < x

—

.1.

Используя

эту оценку, получаем

Ing; —In pj

Pi Pi

(2.19)

(2.20)

Умножив обе части неравенства на pi и просуммировав по всем со-

бытиям 1 < i < N, имеем

(2.21)

,20 Глава 2. Информация, энтропия

избыточность

После упрощения получаем

ад

1п <

" "

=о

•'

нат

л1п

*^|^

А£

и,

следовательно

-S^Pilnqi.

(2.23)

нам

" ^—'

г=1

Предположим, что источник

содержит только равновероятные со-

бытия. Тогда

(2.24)

г=1

Так

как

процессе доказательства на источник

не было наложено

никаких

ограничений, то данное неравенство имеет место для любого

дискретного источника без памяти, содержащего

событий

H(X)<\og

N6nT.

(2.25)

Максимум достигается, когда все события имеют одинаковые веро-

ятности.

•

Любой источник, содержащий TV событий, не все из которых име-

ют одинаковую вероятность, обладает энтропией, меньшей

Iog

./V.

Рассмотрим источник емкостью

Щ =

log

как резервуар для хра-

нения

информации, который никогда

не

переполняется.

Разность

между

максимальной емкостью

#о и

энтропией источ-

ника

содержащего

событий, называется

избыточностью

ис-

точника

= Н

- Н(Х).

(2.26)

Относительная

избыточность

определяется как

Пример:

Энтропия дискретного источника без памяти, содержа-

щего

событий.

2.2.

Энтропия и избыточность

Таблица

2.2.

Дискретный источник без памяти

символами

Xi алфавита

X = {а,

Ь,

с, d,

е, /} с

вероятностью

р;

информацией I[pi).

I(pi)

0,05

4,32

бит

0,15

2,74

бит

0,05

4,32

бит

0,4

1,32

бит

0,2

2,32

бит

0,15

2,74

бит

Для того, чтобы конкретизировать проведенные выше рассужде-

ния,

рассмотрим численный пример.

таблице

2.2

задан дискретный

источник

без

памяти

X с

соответствующими алфавитом

вероят-

ностями событий. Следуя (2.3), подсчитаем информацию каждого

события

дополним таблицу значениями.

Энтропия

источника равна

Н(Х)

= 2,25 бит.

Значение Но

для

событий равно

log

б бит =

2,585

бит,

тогда

избыточность

(log

6-2,25)

бит =

0,335

бит

и,

соответственно, относительная избыточность составляет

2,25

= 1-

Iog

0,130 ^

13%.

(2.28)

(2.29)

(2.30)

(2.31)

Особое значение имеют дискретные двоичные источники

без па-

мяти,

так как в

большинстве случаев

с их

помощью можно описать

процесс передачи данных.

Пусть задан двоичный источник

без

памяти

алфавитом

X =

{0,1} и с

вероятностями

для

символов

«0» и «1» - ро = V

1-ро соответственно. Выбор символов производится независимо.

Его

энтропия,

называемая также функцией Шеннона, зависит только

от

вероятности

р.

Энтропия

двоичного

источника

(функция

Шеннона)

Нь{р)

бит

-plog

- (1 -

р) Iog

р).

(2.32)

Глава

Информация,

энтропия и избыточность

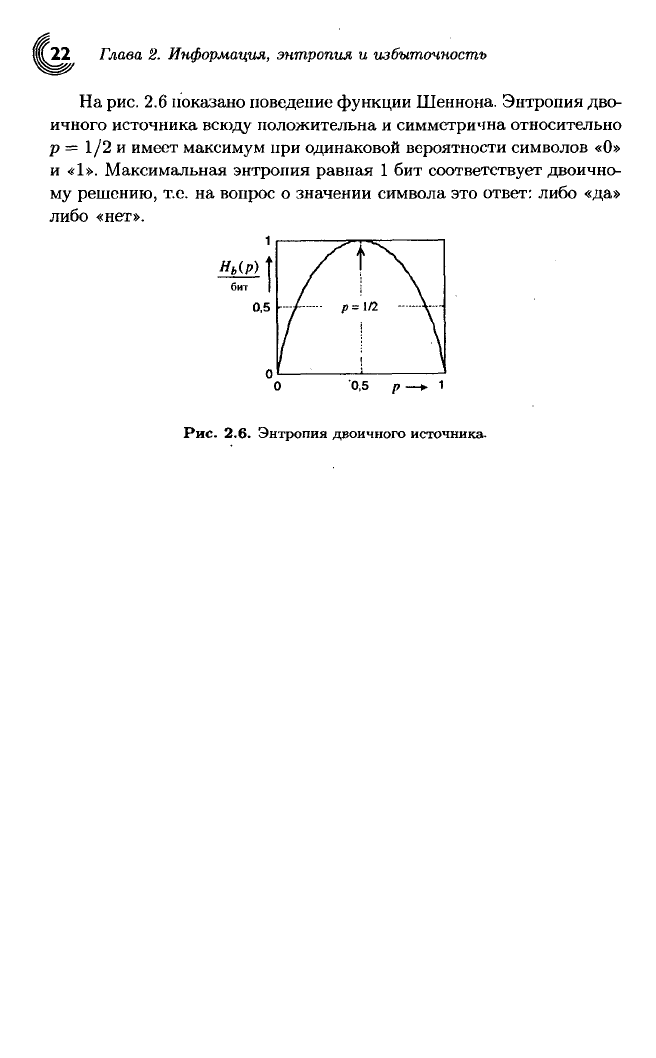
На

рис. 2.6 показано поведение функции Шеннона. Энтропия дво-

ичного источника

всюду

положительна и симметрична относительно

р = 1/2 и имеет максимум при одинаковой вероятности символов «О»

«1». Максимальная энтропия равная 1 бит

соответствует

двоично-

му решению, т.е. на вопрос о значении символа это ответ: либо

«да»

либо

«нет».

0,5 р —i

Рис.

2.6.

Энтропия двоичного источника.